潜油电机整体三维温度场耦合计算与分析
2010-06-06孟大伟刘宇蕾张庆军徐永明
孟大伟, 刘宇蕾, 张庆军, 徐永明
(哈尔滨理工大学电气与电子工程学院,黑龙江 哈尔滨 150040)
0 引言
潜油电机是采油设备的心脏,它连同潜油泵一起工作在地下数千米,环境十分复杂。有些油田的井下温度可达120℃甚至更高。准确的计算潜油电机各部分温度分布,对电机的设计和井下运行具有重要意义。潜油电机受油井套管尺寸限制,机壳直径仅为0.15 m左右,而电机长度一般可达6~10 m。潜油电机采用立式安装,整个转子由上端止推轴承支撑。电机定子采用分段结构,段与段之间装有隔磁段。转子采用多段式鼠笼型结构,各段鼠笼之间装有扶正轴承,电机内气隙充满专用润滑机油。
迄今为止,对潜油电机温升的测定尚无系统、有效的检测手段,大多依赖于数值计算的方法。而以往的计算都是针对电机定子或转子分别进行的,计算过程中假设定转子之间没有热量传递[1]。由于气隙内部充满的润滑油与定转子之间有相对运动,因而定转子与润滑油之间存在对流换热过程。本文在计算过程中充分考虑各种换热过程,建立了电机整体三维模型,依据已知的油井数据资料,采用有限体积法对潜油电机三维稳态温度场及流体场做了耦合分析计算,得到电机整体的温度分布云图。
1 潜油电机整体稳态温度场耦合计算数学模型
潜油电机内部换热过程主要是热传导过程和对流换热过程,对流换热过程分两部分:定子内表面及转子外表面与气隙润滑油的对流换热,机壳外表面与原油对流换热。两部分对流换热过程热边界条件无法预先给定,而是受到流体流速与壁面温度相互作用的制约,因此界面上的温度、热流密度都应该看成是计算结果的一部分,而不是已知条件。这类热边界条件由热交换过程动态的加以决定而不能预先给定的问题,称为耦合传热问题。
为解决上述问题,考虑到流体场和温度场相互制约,本文采用流体场温度场耦合计算的方法。
1.1 计算模型及基本假设
由于沿轴向电机各段彼此独立,分析温度时可单独建立一段定转子模型。另外考虑电机每段上下对称,可以建立半段进行分析。基于以上原因,本文计算模型选择了半段定子、半段转子、半段扶正轴承、半段隔磁段,同时包括此轴向范围内的气隙间的润滑油、机壳以及机壳外流动的原油,如图1所示。
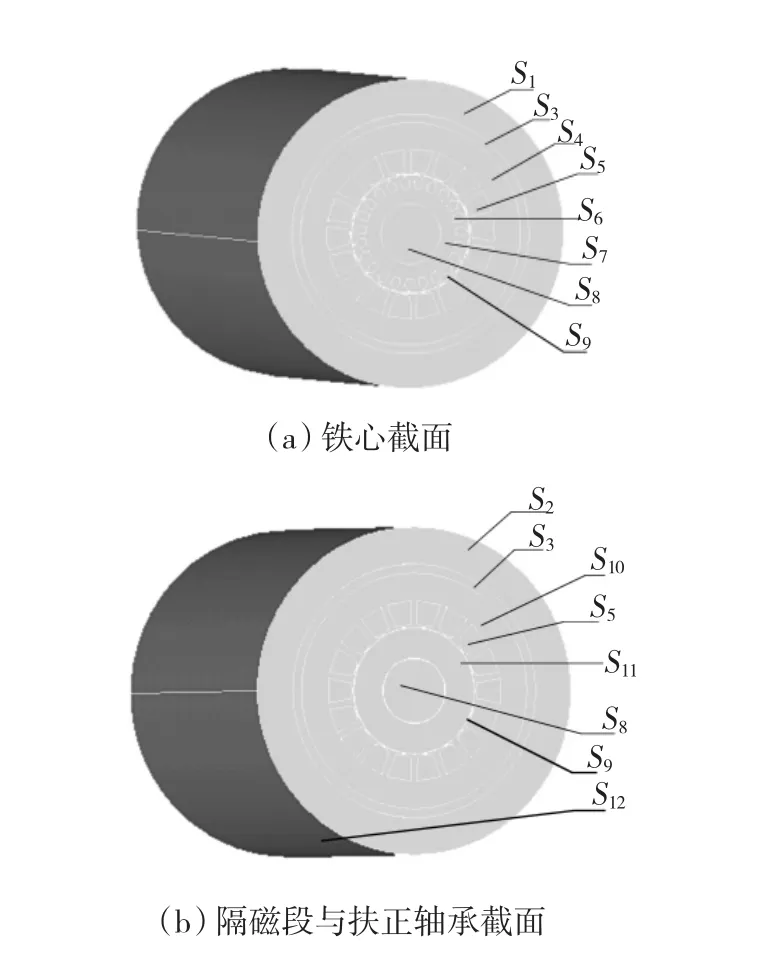
图1 温度场计算三维模型Fig.1 The 3D calculation model of temperature field
计算基本假设:①定子线圈均匀生热;②原油外表面与外界没有热交换;③忽略转子铁心基本铁损耗;④电机机械损耗全部集中定子内表面及转子外表面;⑤忽略润滑油轴向速度。
1.2 耦合场计算边界条件
根据传热学理论,由三维稳态热传导方程和两类边界条件可将三维稳态温度场的边值问题描述为
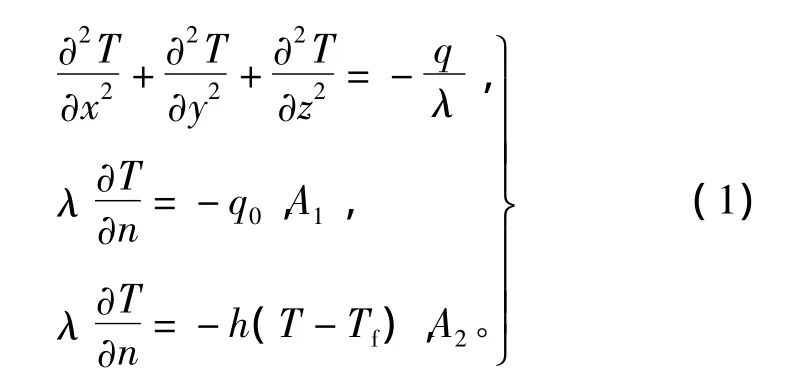
式中:q代表单位体积生热率;T代表固体温度;λ代表导热系数;h代表表面对流换热系数;Tf代表流体平均温度;q0代表热流密度;A1代表热流密度已知的第一类边界,当q0为零时为绝热边界面;A2代表对流传热的第二类边界。
潜油电机换热过程流体温度随换热状态变化,属于耦合传热,因此不能采用上述第二类边界条件。本文采用耦合边界的分区求解方法,耦合边界上的条件可以取下列三种表达式中的任意两个:
1)耦合边界上温度连续:

2)耦合边界上热流密度连续:

3)耦合边界上的第三类边界
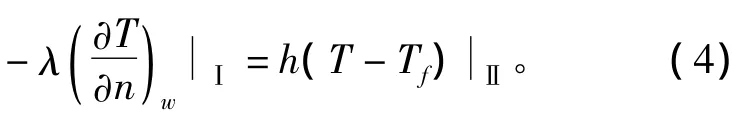
对于以上三种情况,区域Ⅰ代表固体,区域Ⅱ代表流体。假定耦合边界上的温度分布,对其中一个区域(例如Ⅰ)进行求解,得出耦合边界上的局部热流密度和温度梯度,然后应用式(3)或式(4)所得到边界条件求解另一个区域Ⅱ,以得出耦合边界上新的温度分布,再以此分布作为区域Ⅰ的边界条件,重复上述计算直到收敛。
基于以上分析,本文计算模型具体边界条件分别为:①图2中S3~S12截面为绝热面,即第一类边界条件;②对流传热采用耦合传热边界,图2中S1面和S2面分别作为流体的入口和出口。
2 温度场热源的确定
通过电磁计算可计算出定子铁损耗、定转子绕组铜损耗、附加损耗[4]。电机转子在润滑油中高速旋转,其机械损耗主要包括三部分:润滑油与定转子的摩擦损耗、扶正轴承的摩擦损耗、止推轴承动块静块的摩擦损耗,其中起主要作用的是定转子摩擦损耗[5]。根据本文的计算模型,只考虑润滑油与定转子的摩擦损耗对温度的影响。
根据以上方法计算出电机各部分损耗后将其转换成生热率赋给相应的生热部位,表1给出以YQY-143系列40 kW电机为例对应数据。附加损耗按产生部位计算分别与其他损耗相加后赋予相应的部位。

表1 损耗值和生热率Table 1 The loss and heat generation rate
3 温度场计算
图2所示为计算模型网格剖分图,共有583481个节点。
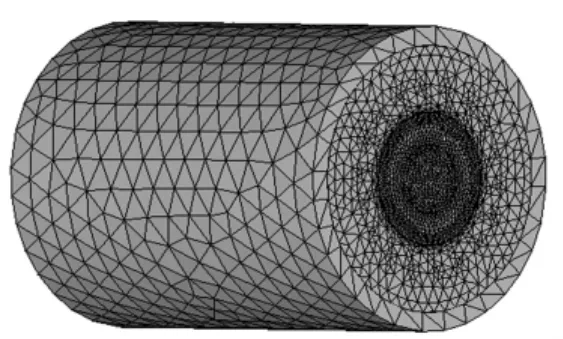
图2 计算模型网格剖分图Fig.2 The mesh graph of the calculation model
根据假设条件以及计算所得到的数值设置边界条件,包括各部分热源、材料属性、流体出口和入口条件。考虑到原油流速对散热的影响,本文中原油流动速度采用国际规定最低速度0.3 m/s这种最不利的散热条件进行计算。
本文对工作在120℃井温情况的YQY-143系列40 kW潜油电机进行分析,得到电机各部分温度情况,分别提取了电机定转子铁芯、定子线圈、转子导条以及电机外壳的温度分布图,如下列各图所示。
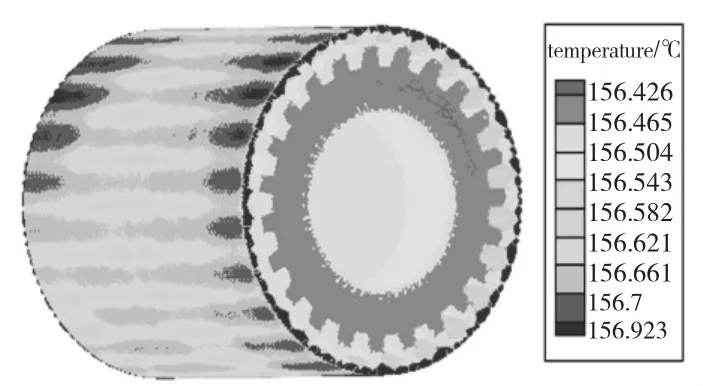
图3 转子铁芯温度分布图Fig.3 Temperature distribution of rotor iron core
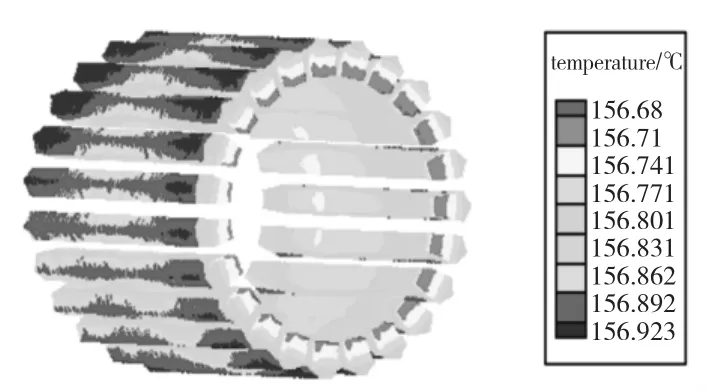
图4 转子导条温度分布图Fig.4 Temperature distribution of copper bar

图5 定子铁芯温度分布图Fig.5 Temperature distribution of stator iron core

图6 定子线圈温度分布图Fig.6 Temperature distribution of stator coil

图7 机壳温度分布图Fig.7 Temperature distribution of Chassis
为验证计算准确性,将本文方法计算所得温度最高值与应用有限体积方法计算所得温度最高值进行对比,如表2所示,可以看出,两组计算值基本相符。
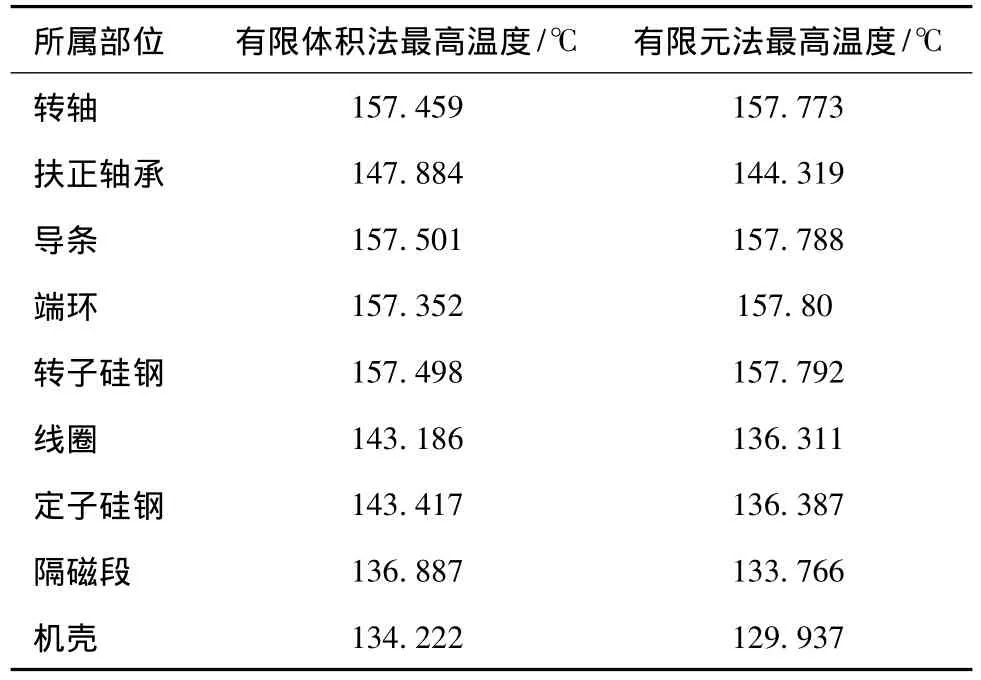
表2 两种方法电机最高温度对照Table 2 The max temperature contrast with two methods
4 结论
1)本文通过有限体积法计算潜油电机三维耦合场,得到电机各部分温度分布情况。通过与有限元法计算值对照,可以看出两种方法计算所得电机各部分温度基本一致。
2)通过分析可知,以运行于120℃井温环境的YQY-143系列40kW电机为例,本文按照最不利散热情况计算得到结果表明该电机内部温度没有过热点,电机中的几个发热部件在额定运行时的温度在该系列电机绝缘等级F级的规定极限温度范围内,可以保证电机安全稳定运行。
[1]孟大伟,刘瑜,徐永明.潜油电机转子三维温度场分析与计算[J].电机与控制学报.2009,13(3):367-370.MENG Dawei,LIU Yu,XU Yongming.Three-dimensional temperature field analysis and calculation of Submersible motor rotor[J].Electric Machines and Control,2009,13(3):367 -370.
[2]魏永田,孟大伟,温嘉斌.电机内热交换[M].北京:机械工业出版社,1998:321-322.
[3]陶文铨.数值传热学[M].2版.西安交通大学出版社,2001:484-486.
[4]孟大伟,徐永明,温嘉斌.潜油电机设计方法改进研究[J].石油学报,2007,28(3):127-130.MENG Dawei,XU Yongming,WEN Jiabin.Research on improvement of submersible motor design method[J].Acta Petrolei Sinica,2007,28(3):127-130.
[5]徐永明,孟大伟.潜油电机机械损耗的分析与计算[J].电机与控制学报,2004,8(4):370-372.XU Yongming,MENG Dawei.The mathematical loss copulation of the submersible motor[J].Electric Machines and Control,2004,8(4):370-372.
