直驱式电液伺服转叶舵机退火蚁群寻优PD控制

苏文海， 姜继海， 刘庆和

(1.东北农业大学工程学院，黑龙江 哈尔滨 150030;2.哈尔滨工业大学机电工程学院，黑龙江 哈尔滨 150080)

0 引言

转叶舵机具有设计紧凑、安装方便、占用空间小等优势［1－2］，在许多大型艉机型船舶和军舰上得到了广泛的应用，是很有前景的舵机形式。传统的转叶舵机控制方式主要有比例阀控制和变量泵控制两种方式，这两种方式由于采用精密液压元件，对液压系统的清洁度要求非常高，而且控制系统复杂，控制元件多，容易发生故障［3］。针对传统的转叶舵机伺服系统的弊端，提出并制造了直驱式电液伺服转叶舵机的原理样机。该型式舵机和传统的转叶舵机相比，用变频电机驱动定量泵取代了异步电机驱动变量泵或者伺服阀的控制方式，对系统清洁度的要求大大降低。同时，直驱式电液伺服舵机去掉了泵站和管路，减少了控制元件，使得占地面积更小、系统的可靠性更高，节约能源且绿色环保。

直驱式电液伺服转叶舵机结构紧凑、节约能源且易于安装，是新型高效的舵机形式。但是，直驱式电液伺服转叶舵机是一种具有强非线性的电液位置伺服系统，其转动惯量大、液压系统能够调节死区、水动力负载复杂，呈现出时变特性和随机性，传统的PD控制器参数整定不良、性能欠佳，已经不能满足直驱式电液伺服转叶舵机的控制需求，因此需要一种智能的参数根据运行工况不同而在线整定的PD控制器。

目前PID参数的智能优化方法很多，主要有专家整定法和遗传算法整定法两种。专家整定法需要太多的经验，整理专家库是一项长时间的工程，需要大量的前期准备工作。遗传算法具有良好的寻优特性，对初始值不敏感，可避免过早陷入局部最优解，但遗传算法对系统中的反馈信息利用不够，当求解到一定范围时往往做大量无功的冗余迭代，求解效率低，在线整定时间相对较长。为了提高直驱式电液伺服舵机的响应速度和鲁棒性，改善舵机系统对输入信号的跟踪性能，引进蚁群寻优的PD控制技术，将模拟退火算法与改进的蚁群算法相结合，提出基于模拟退火(simulated annealing，SA)算法［4－5］的蚁群寻优［6－8］PD智能算法，并将其应用到直驱式电液伺服转叶舵机控制系统中。该算法在蚁群算法正反馈机制的基础上，通过模拟退火策略来提高控制器跳出局部极值点、进入全局最优解所在区域的能力，提高求得全局最优解的可靠性。在直驱式电液伺服转叶舵机原理样机及其加载实验台上进行在线实验。

1 直驱式电液伺服转叶舵机

直驱式电液伺服转叶舵机的原理图如图1所示。直驱式电液伺服舵机主要由3部分组成:计算机控制部分、电动机伺服调速部分及液压动力机构。计算机控制部分对位移传感器的采集信号进行信号处理，由系统主控制器计算处理后，经D/A数模转换为电压信号输出到变频器，驱动电机控制液压动力机构，从而控制负载。通过改变变频电机的正反转、运动速度和运转时间控制液压执行机构的正反向、运动速度和位置，该方案可以充分发挥变频调速系统的优势。由于直驱式电液伺服转叶舵机中没有使用电液伺服阀和变量泵，使得直驱式电液伺服转叶舵机抗污能力强，可靠性高，寿命长，节能高效。直驱式电液伺服转叶舵机可以视为一种大功率大惯性的变频泵控马达调速系统，由于大的转动惯量和液压系统的调节死区和负载的时变特性等因素的影响，使得控制系统存在较大的时滞，控制系统响应慢，动、静态性能比较差。

图1 直驱式电液伺服转叶舵机组成原理图Fig.1 Principle sketch of direct drive electro-hydraulic servo rotary vane steering gear

2 退火蚁群寻优PD智能控制器设计

PD智能控制器是在最大最小蚂蚁算法(maxmin ant system，MMAS)的基础上，通过模拟退火策略来决定何种蚂蚁被允许释放信息素，以一定的概率接受性能较差解，使得控制器具有跳出局部极值点、进入全局最优解所在区域的能力，从而避免蚂蚁算法早熟，有利于提高求得全局最优解的可靠性，得到PD控制参数的最优解。

2.1 不完全微分PD控制

在常规PID转向控制响应中，由于积分控制的作用，船舶在到达预定航向前存在一个较大的超调，所以舵机控制系统多采用PD控制。PD控制虽然没有超调，但是存在稳态误差，也容易引进高频干扰，使得舵机频繁动作，影响舵机系统的稳定性。解决此缺点的方法是在PD控制器中加入一个一阶惯性环节(低通滤波器)，其传递函数为

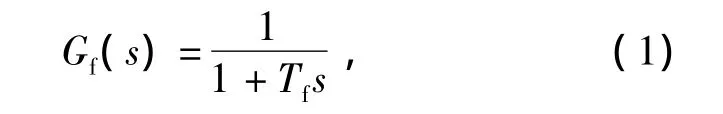
式中Tf为滤波器时间常数。具有一阶惯性环节的微分控制称为不完全微分控制。不完全微分控制的PD控制器的传递函数可以表示为

式中:Kp为比例系数;Td为微分时间常数;Ts为采样时间;E(s)为输入与输出之间的误差;U(s)为控制量。在离散域内，增量式不完全微分PD控制律可表示为

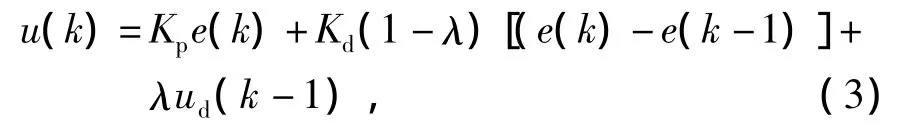
式中:Kp为比例系数;Kd为微分系数，Kd=KpTd/Ts;λ为常数，且λ=Tf/(Tf+Ts)<1;e(k)为输入与输出之间的误差。与传统PD控制器相比，不完全PD控制器的算法复杂，具有良好的控制性和鲁棒性。

2.2 节点和路径的生成

以PD控制器的2个参数Kp和Kd作为待优化的变量，根据直驱式电液伺服转叶舵机的具体情况，设置Kp具有4位有效数字，其中小数点前占1位，小数点后占3位，Kd具有4位有效数字，其中小数点前后各占2位。图2所示的可爬行节点(指虚线区域内)，交点K(xi，yi，j)为蚂蚁可到达的节点，其中:i取1～8中的整数，j取0～9中的整数，L1～L8为平行Y轴的线段。蚂蚁由原点依次历经(x1，y1，j)→(x2，y2，j)→(x3，y3，j)→ (x4，y4，j)→(x5，y5，j)→(x6，y6，j)→(x7，y7，j)→(x8，y8，j)形成爬行路径，yi，j为节点在线段 Li上的纵坐标，其中 y1，j～ y4，j和 y5，j～y8，j分别为Kp和Kd第1到第4位上的数字。图2所示的爬行路径所表示的PD参数的值为:Kp=3.934，Kd=71.29。

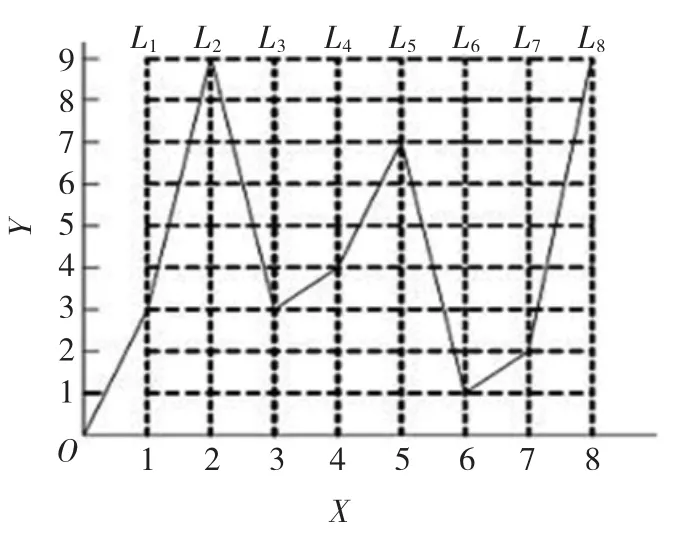
图2 节点及路径示意图Fig.2 Sketch map of knot and path

2.3 确定目标函数

为使系统具有良好的响应速度和准确性，采用误差绝对值时间积分性能指标作为评价控制系统优劣的性能指标，其最优控制系统具有优良的系统响应特性。蚂蚁s的目标函数f(s)为

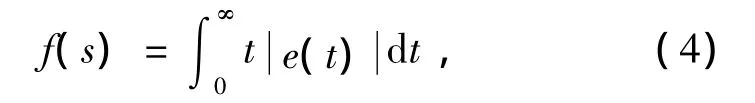
式中e(t)为输出与输入的误差值。

2.4 路径点的选择

假设每只蚂蚁从线段Li上任意节点爬行到Li+1上任意节点时间相等，则所有蚂蚁同时从原点O出发，同时历经各线段Li并同时到达终点，完成一次循环［9］。设蚂蚁总数为 n，τ(xi，yi，j，t)表示 t时刻在节点K(xi，yi，j)上遗留的信息量，初始时刻各节点上的信息量相等，即 τ(xi，yi，j，0)=c，c 为常数，τ(xi，yi，j，0)=0。设第 k 只蚂蚁由 Li－1上任一点爬行至K(xi，yi，j)的路径选择概率为(t)，则有

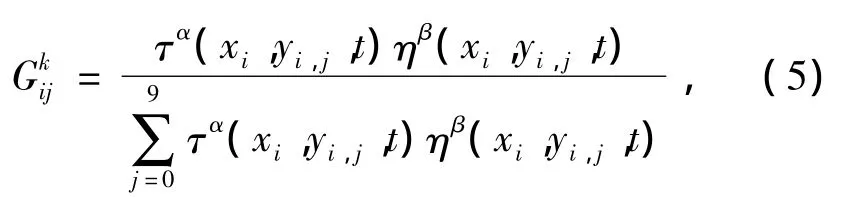
式中:α为信息启发式因子;β为期望启发式因子;分别表示信息素的浓度和能见度在转移概率中的相对重要性。η(xi，yi，j，t)为节点 K(xi，yi，j)上的能见度，且有

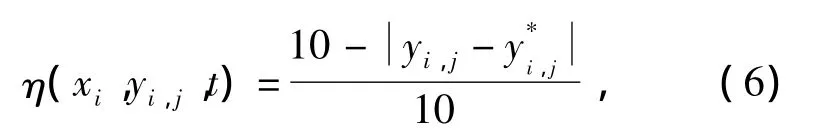
2.5 初始温度及温度更新函数

n个人工蚁完成第一次爬行后，确定爬行最优路径(一次爬行路径中目标函数值最小的路径)及其误差绝对值时间积分性能指标cbest，和周游最差路径(一次周游路径中目标函数值最大的路径)及其误差绝对值时间积分性能指标cworst。确定初始温度 t0= －(cworst－cbest)/ln p0，其中的 p0∈［0，1］为初始接受概率。退温函数采用指数退温策略tk+1=δtk，δ∈(0，1)为退温速率。这种退温策略能较好地折衷、兼顾优化质量和时间性能。

2.6 信息素的更新

最大最小蚂蚁算法中，只有构建出迭代以来最优路径的蚂蚁或在本次迭代中构建出最优路径的蚂蚁才被允许更新信息素。使用迭代以来最优蚂蚁更新策略，系统收敛很快。但由于正反馈现象的存在，蚂蚁在最初的搜索步骤中可探索的路径较少，在后期的搜索中易于陷入停滞状态。而使用本次迭代最优蚂蚁更新策略，减少了搜索的导向性、增加了搜索能力，但是系统收敛速度较慢。在最大最小蚂蚁算法中引入退火策略，可以在不同概率下采用不同的更新策略解决此问题。

全部蚂蚁在t+1时刻完成一次爬行后，则各节点信息量 τ(xi，yi，j，t+1)为

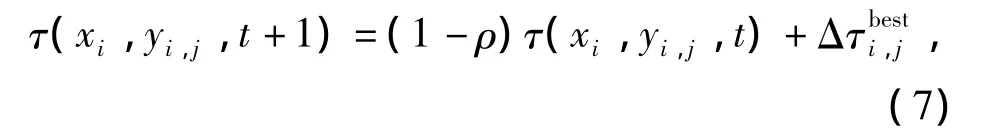
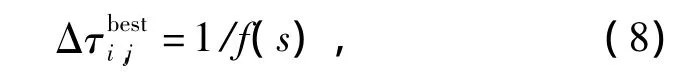
式中f(s)为蚂蚁s的目标函数值。设本次迭代最优蚂蚁为sib，至今迭代最优蚂蚁为sgb，在每次迭代中信息素更新时，以概率Psa来使用本次迭代最优蚂蚁更新策略，以(1－Psa)的概率来使用至今迭代最优蚂蚁更新策略，有

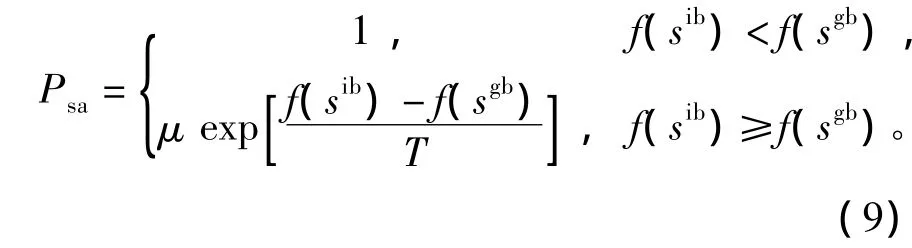
式中:T为退火温度的参数;μ为退火强度的参数。在算法运行的过程中，T逐渐减小，用以减少接受本次迭代最优蚂蚁的概率。为保证算法的收敛速度，退火强度μ取一个较小的数。引入退火策略后，可以看出，在搜索早期，使用本次迭代最优蚂蚁更新策略的概率较大，增加了解的多样性和算法的搜索能力。在搜索中后期，由于初始解的多样性已使得蚂蚁有多种选择，此时增大使用接受迭代以来最优蚂蚁更新策略的概率可以加快收敛速度。由于MMAS陷入停滞时，信息素矩阵还会被重新初始化，所以还可以使用多次退火策略。一个退火循环完成后，可将温度重置为T0′，开始新的退火循环。

设信息素的取值范围为［τmin，τmax］，则有

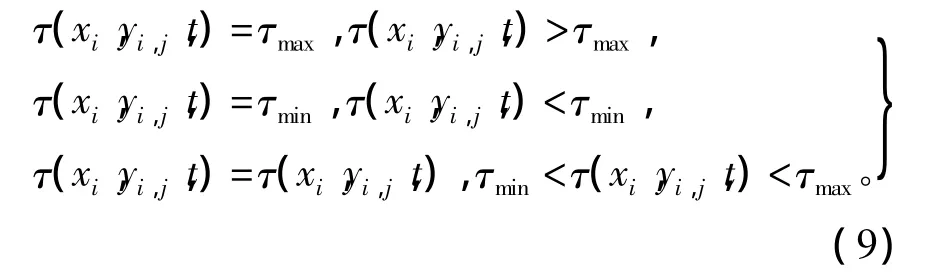
2.7 基于模拟退火的最大最小蚁群算法

图3 基于模拟退火的最大最小蚁群算法流程图Fig.3 Flow process sheet of SAMMAS

基于模拟退火的最大最小蚁群算法流程图如图3所示。由图3可以看出，MMAS为SA提供了一系列的初始解，使得SA的邻域搜索能力进一步改善解，同时MMAS利用SA产生的新解再进行并行搜索。因此，基于模拟退火的最大最小蚁群算法结合了模拟退火和最大最小蚁群算法的特点，增强了这两种算法的搜索能力，弥补了算法的弱点［10］。

3 实验研究

基于理论分析编写控制算法程序，在最大输出扭矩320×103N·m的直驱式电液伺服转叶舵机原理样机及其加载实验台上进行实验。为了验证所提出的控制策略的有效性，需要考察系统对不同负载的补偿特性和对干扰的抑制特性，以及系统的低速跟踪特性。为此，实验部分首先给出阶跃响应实验以验证控制算法对不同负载的补偿能力及对干扰的抑制能力，然后进行斜坡响应实验验证控制器的低速稳定性。实验中，取Ts=20ms;Tf=0.5 s;n=30;ρ=0.4;α =1.5;β=1.5;p0=0.8;δ=0.7;μ =0.2。

阶跃响应如图4所示。由图4中的曲线1和曲线2可以看出，当负载变化时，相对于Z-N法整定的PD控制器，本文所设计的控制系统具有更好的稳态精度，稳态误差保持在±0.05°范围内，并且调整过程变化小，上升时间也比较小，说明所设计的PD控制器具有很强的鲁棒性。曲线3和曲线4的稳态误差均超过±0.05°。

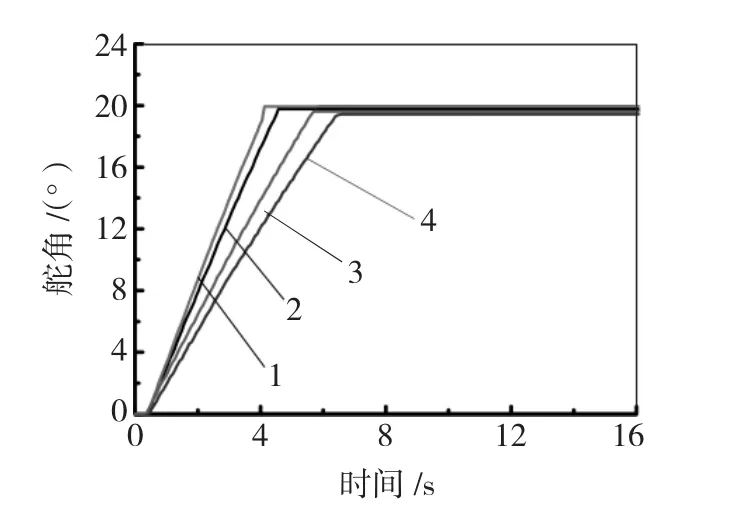
图4 阶跃响应Fig.4 Step response of system

影响直驱式电液伺服转叶舵机的低速性能的主要因素是转叶马达的泄漏与非线性摩擦，具体表现为低速爬行。图5为系统跟踪斜率为0.01(°)/s的斜坡信号时的响应曲线。由图5可以看出，采用Z-N法整定的PD控制器时，系统出现爬行和较大的滞后现象。采用退火蚁群寻优PD控制器时，爬行得到抑制，滞后时间也缩短到1 s以内，表明退火蚁群寻优的PD控制器能补偿马达的泄漏和抑制摩擦干扰。

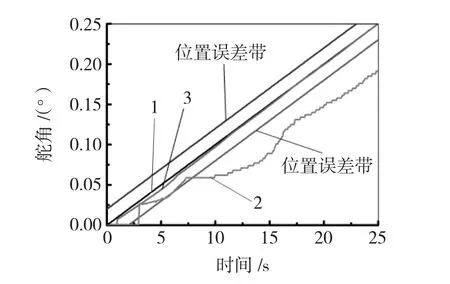
图5 斜坡响应Fig.5 Ramp response of system

4 结语

采用基于退火策略的蚁群优化算法设计了直驱式电液伺服转叶舵机控制参数实时整定的不完全微分PD控制器。该控制器具有最大最小蚂蚁算法和模拟退火算法复合优点，具有大范围快速全局搜索能力且求解能力高，避免蚂蚁算法早熟，能满足实时控制参数整定需求。实验结果表明基于退火蚂蚁群算法的PD控制器具有良好的动态性能和鲁棒性能，能有效地提高直驱式电液伺服转叶舵机的控制精确度。

［1］MARTINS M R，NATACCI F B.Reliability analysis of a rotary vane type steering gear system［C］//Proceedings of the Eighteenth International Offshore and Polar Engineering Conference，July 6－11，2008，Vancouver，Canada.2008:478 －483.

［2］苏文海，姜继海，刘庆和.直驱式电液伺服转叶舵机系统分析及仿真［J］.东北大学学报:自然科学版，2008，29(S1):244－247.SU Wenhai，JIANG Jihai，LIU Qinghe.Direct drive electric-hydraulic servo rotary vane steering gears system analysis and simulation［J］.Journal of Northeastern University:Natural Science，2008，29(S1):244－247.

［3］祁联仲.舵机液压油污染的分析及控制［J］.海军航空工程学院学报，2006，21(6):618－622.QI Lianzhong.Analysis and control the hydraulic oil contamination of actuator［J］.Journal of Naval Aeronautical Engineering Institute，2006，21(6):618－622.

［4］ANDO Keiko，MIKI Mitsunori，HIROYASU Tomoyuki.Multipoint simulated annealing with adaptive neighborhood［J］.IEICE Transactions on Information and Systems E Series D，2007，90(2):457－464.

［5］LUO Yazhong，TANG Guojin.Spacecraft optimal rendezvous controller design using simulated annealing［J］.Aerospace Science and Technology，2005，9(8):732 －738.

［6］DEMIREL N C，TOKSAN M D.Optimization of the quadratic assignment problem using an ant colony algorithm［J］.Applied Mathematics and Computation，2006，183(1):427－435.

［7］FOX Bud，XIANG Wei，LEE Heowpueh.Industrial applications of the ant colony optimization algorithm［J］.The International Journal of Advanced Manufacturing Technology，2007，31(7/8):805－814.

［8］段海滨，王道波，于秀芬.基于云模型的小生境MAX-MIN相遇蚁群算法［J］.吉林大学学报:工学版，2006，36(5):803－808.DUAN Haibin，WANG Daobo，YU Xiufen.MAX-MIN meeting ant colony algorithm based on cloud model theory and niche ideology［J］.Journal of Jilin University:Engineering and Technology E-dition，2006，36(5):803－808.

［9］谭冠政，李文斌.基于蚁群算法的智能人工腿最优PID控制器设计［J］.中南大学学报:自然科学版，2004，35(1):91－96.TAN Guanzheng，LI Wenbin.Design of ant algorithm-based on optimal PID controller and its application to intelligent artificial leg［J］.Journal of Central South University:Science and Technology，2004，35(1):91－96.

［10］冯远静，冯祖仁，彭勤科.智能混合优化策略及其在流水作业调度中的应用［J］.西安交通大学学报，2004，38(8):779－782.FENG Yuanjing，FENG Zuren，PENG Qinke.Intelligent hybrid optimization strategy and its application to flow-shop scheduling［J］.Journal of Xi’an Jiaotong University，2004，38(8):779－782.