双边空心式永磁直线伺服电机的空载磁场分析

刘晓， 张玉秋， 叶云岳， 卢琴芬

(浙江大学电气工程学院，浙江 杭州 310027)

0 引言

近年来，直线伺服电机得到了快速的发展和广泛的应用。永磁直线伺服电机同时具备了永磁电机和直线电机的优点，结构简单、体积小、噪音低、效率高、动态性能好，且对工作环境适应性好、易维护，尤其是“零传动”的特点，使其逐渐成为直线伺服系统的研究热点［1－2］。由于一般的铁心式永磁直线电机受到齿槽效应和端部效应的影响，输出推力有比较大的波动，引起电机振动和噪音，严重影响其伺服性能，需通过优化设计降低其推力波动［3－6］。空心式永磁直线电机则不存在齿槽效应和铁心开断的影响，输出推力较铁心式永磁直线电机更稳定，但受电机气隙谐波磁场的影响，空心式永磁直线电机仍然存在推力波动的问题。

为了对电机进行优化设计，减小推力波动，必须对电机气隙磁场进行求解和分析，文献［7－9］分别推导了空心式永磁直线电机的气隙磁场解析公式，但解析解存在解析公式复杂以及求解精确度不高等问题。本文采用等效磁化强度法对电机的气隙磁场进行解析求解，并将解析分析结果与有限元分析结果进行比较。根据解析公式，分析了电机几个主要尺寸对气隙磁场的影响。

1 电机拓扑结构

双边空心式永磁直线伺服电机的二维拓扑结构如图1所示。

图1 双边空心式永磁直线伺服电机拓扑结构图Fig.1 Topology of the double side air-core PMLSM

该电机结构由动子和定子两部分组成，线圈安装在动子上，属于动圈式结构形式。定子部分由永磁体和铁轭构成，永磁体分别贴装在2个定子铁轭侧壁内侧，形成一个类似“U”型的双边结构，永磁体极性如图1所示。双边型结构使电机不存在法向力，减少了动子运动时的摩擦力，也降低了对直线导轨和安装的要求。电机动子部分由三相绕组构成，绕组采用空心式线圈，线圈整体用环氧树脂进行封装，既保证电机动子部分的整体性，又对线圈起到保护作用。绕组采用5极/3线圈的短距集中绕组形式，减小绕组端部长度，提高了电机的效率并减轻了动子质量。

2 气隙磁场解析分析

为简化分析，对电机分析模型做如下假设:

1)假设电机在z方向无限长;

2)假设电机初级在x方向无限长;

3)假设铁磁材料的磁导率为无穷大。

基于以上假设，可以将该电机气隙磁场的求解问题简化为具有铁磁边界的二维恒定磁场进行求解。

等效磁化强度法将永磁体等效成磁化强度，根据材料不同将整个求解区域划分为气隙区域和磁极区域，向量磁位A在气隙区域满足拉普拉斯方程，在磁极区域则满足泊松方程，可以分别求解。在二维平面场中，向量磁位A只有Az分量，大大降低了方程的数量和求解的难度。该电机的等效磁化强度向量分析模型如图2所示，根据电机结构的对称性，仅选择电机上半部分进行分析，进一步简化求解过程。永磁体的等效磁化强度向量的空间分布如图3所示。

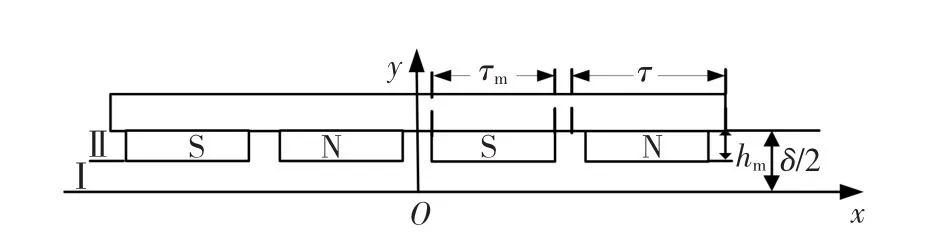
图2 等效磁化强度法分析模型Fig.2 Analytical model of the equivalent magnetization intensity method

图3 磁化强度空间分布Fig.3 Distribution of the magnetization intensity

等效磁化强度空间分布函数M(x)可以用傅立叶级数表示为

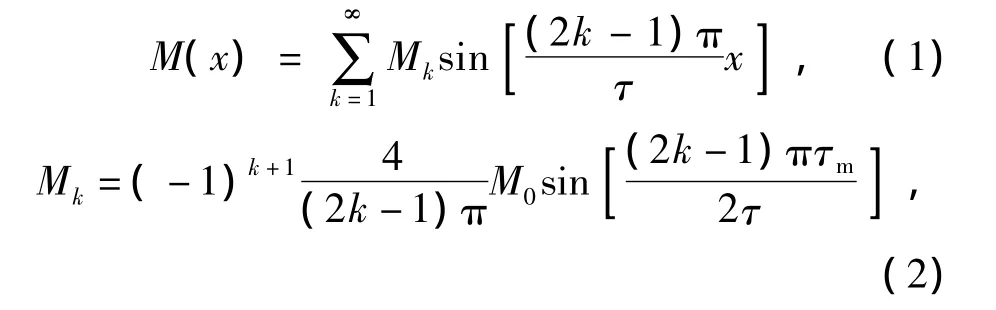
在气隙区域Ⅰ中，向量磁位AzⅠ满足拉普拉斯方程，在磁极区域Ⅱ中，向量磁位 AzⅡ满足泊松方程［10］

在气隙和磁极的交界面上，满足边界条件:

磁场强度在切向方向上连续，即

磁通密度在法向方向上连续，即

根据假设3)，在铁轭表面满足边界条件:

铁轭表面磁密切向分量为零，即

采用分离变量法求解，得到各区域中向量磁位的表达式为

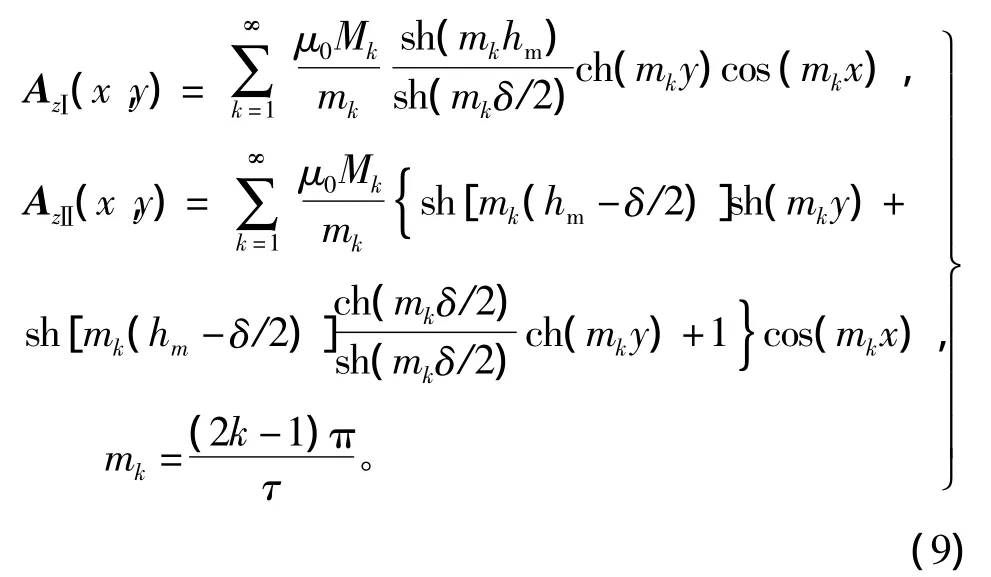
通过对向量磁位求偏导，得到各区域磁通密度法向分量的表达式为

3 有限元分析验证

利用Ansoft Maxwell软件建立电机模型，电机参数为:极距τ=22 mm;永磁体宽τm=18 mm;永磁体高hm=3.6 mm;气隙δ=14.6 mm。对电机进行有限元分析，得到电机空载时气隙磁场磁力线分布如图4所示。

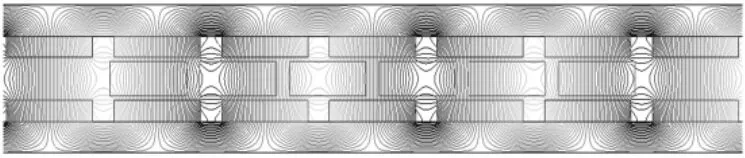
图4 气隙磁场磁力线分布图Fig.4 Distribution of magnetic line in airgap

为验证解析法计算结果的准确性，分别用解析法和有限元法计算出y=0，y=1和y=6三个位置上磁通密度y向分量By值，并将其分布曲线绘于图5～图7中，进行比较。由图5、图6可以看出，在区域Ⅰ中(y=0，y=1)解析法与有限元法的计算结果非常接近;由图7可以看出，在区域Ⅱ中(y=6)，解析法求解的误差稍大。为进一步验证解析法的正确性，改变永磁体宽度τm，计算出不同的τm/τ时，解析法与有限元法计算结果在一个极距范围内的平均相对误差，如表1所示。解析法的最大相对误差为3.71%，证明该解析法求解结果是准确的。

图5 y=0处气隙磁密分布图Fig.5 Distribution of magnetic flux density at y=0

图6 y=1处气隙磁密分布图Fig.6 Distribution of magnetic flux density at y=1

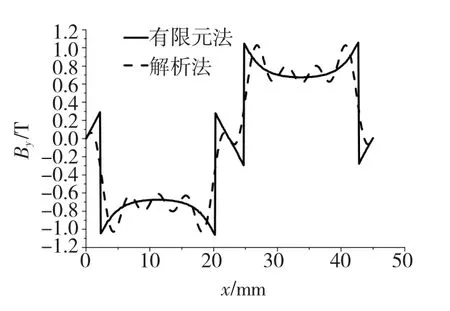
图7 y=6处气隙磁密分布图Fig.7 Distribution of magnetic flux density at y=6

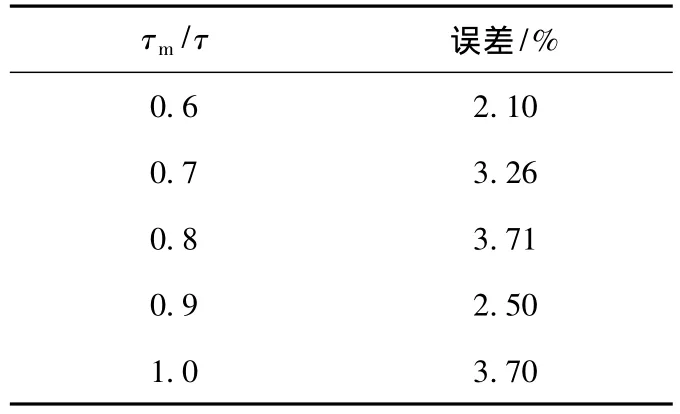
表1 不同的τm/τ时解析法的误差Table1 Errors of the analytical method with different τm/τ

4 主要尺寸对气隙磁场的影响

取气隙中心线处(y=0)磁场作为分析对象，根据式(10)，可以求得该处磁通密度基波和各次谐波分量的幅值为

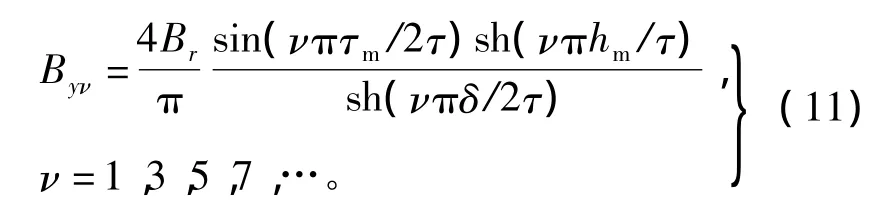
根据式(11)，可以看出Byν与3个主要尺寸永磁体宽度τm、永磁体高度hm和气隙高度δ有关，分别定义极弧系数αp=τm/τ，磁极高度系数β=hm/τ和气隙高度系数γ=δ/τ，分析3个系数对磁场分布情况的影响。

4.1 极弧系数对气隙磁场的影响

首先保持β和γ不变，将Byν对于αp求导，为

当 ναp=2n，n=1，2，3，…时=0，Byν取到最小值。第3、5、7、9 次谐波 Byν与 αp关系如图8 所示，各次谐波分量与基波幅值的比值Byν/By1与αp的关系如图9所示。以总谐波磁场与基波磁场的比值∑Byν/By1作为衡量气隙磁场正弦程度的标准，得到气隙磁场谐波含量随αp变化的曲线如图10所示。由图10可以看出，当αp=2/3时，∑Byν/By1达到最小值，气隙磁场的谐波含量最小。在电机设计时，选取αp在0.6～0.8之间，可以有效地降低气隙磁场的谐波含量。

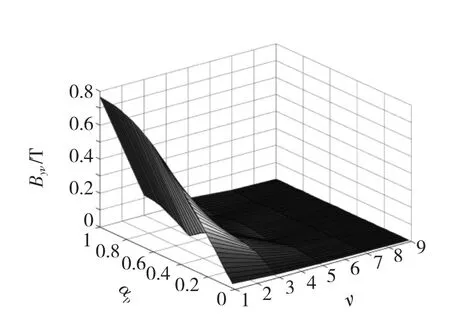
图8 Byν与 αp 关系图Fig.8 Relationship between Byν and αp

图9 Byν/By1与 αp 关系图Fig.9 Relationship between Byν /By1and αp

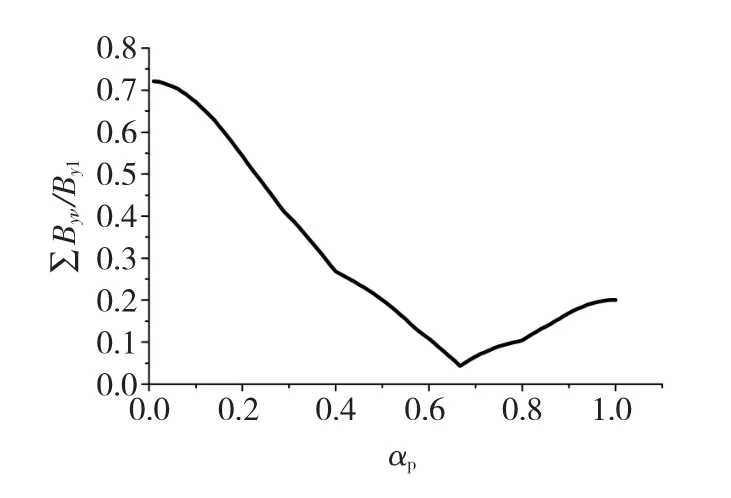
图10 ∑Byν/By1与 αp关系图Fig.10 Relationship between ∑Byν/By1and αp

4.2 磁极高度系数和气隙高度系数对气隙磁场的影响

根据式(11)，Byν是关于磁极高度系数β的单调增函数，随着β的增大，气隙磁场谐波含量也将增大。同时，Byν是关于气隙高度系数γ的单调减函数，气隙磁场谐波含量随γ的增大而减小。保持αp=2/3不变，Byν随β和γ变化的曲线分别如图11和图12所示，∑Byν/By1随β和γ变化的曲线分别如图13和图14所示。

图11 Byν与 β 关系图Fig.11 Relationship between Byν and β

图12 Byν与 γ关系图Fig.12 Relationship between Byν and γ

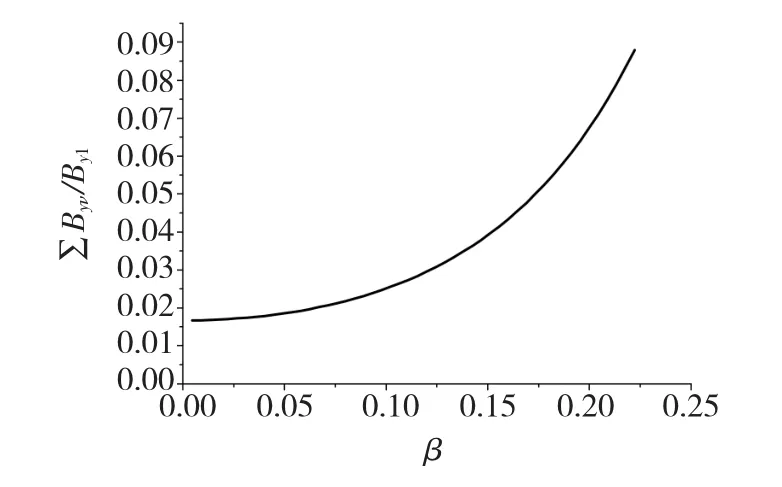
图13 ∑Byν/By1与 β关系图Fig.13 Relationship between ∑Byν/By1and β

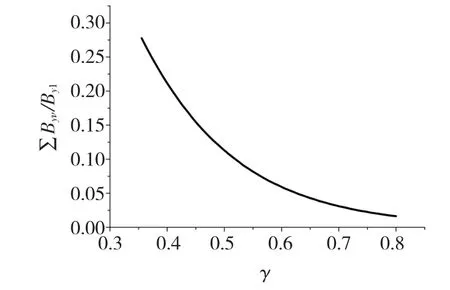
图14 ∑Byν/By1与γ关系图Fig.14 Relationship between ∑Byν/By1and γ

一般来说，为提高电机的推力密度，希望获得较大的气隙磁密，增加永磁体高度和减小气隙高度都是加大气隙磁密的手段，但同时也降低了气隙磁场分布的正弦性。与极弧系数对气隙磁场分布正弦程度的影响相比，磁极和气隙高度系数的影响较小，所以，在电机设计时，应主要考虑磁极高度系数β和气隙高度系数γ对气隙磁密大小的影响，同时通过优化极弧系数αp来降低气隙磁场的谐波含量。

5 结语

对于双边空心式永磁直线伺服电机的气隙磁场，采用等效磁化强度法和有限元法的求解结果的最大相对误差为3.71%，该解析方法可用于对双边空心式永磁直线伺服电机进行磁场和特性分析。对该电机的解析分析表明，电机永磁体高度hm和气隙高度δ主要影响气隙磁场的大小，而永磁体宽度τm对电机气隙磁场的大小和谐波含量都有很大影响。当极弧系数αp=2/3时，电机气隙磁场的谐波含量最小，一般在设计该类型电机时，可以选取αp=0.6～0.8。

［1］叶云岳.直线电机原理与应用［M］.北京:机械工业出版社，2000:102－135.

［2］叶云岳，卢琴芬，范承志，等.直线电机技术手册［M］.北京:机械工业出版社，2003:79－83.

［3］ZHU Z Q，XIA Z P，HOWE D，et al.Reduction of cogging force in slotless linear permanent magnet motors［J］.IEE Proceedings-Electric Power Applications，1997，144(4):277 －282.

［4］HOR P J，ZHU Z Q，HOWE D，et al.Minimization of cogging force in a linear permanent magnet motor［J］.IEEE Transactions on Magnetics，1998，34(5):3544－3547.

［5］KIM M Y，KIM Y C，KIM G T.Design of slotless-type PMLSM for high power density using divided PM［J］.IEEE Transactions on Magnetics，2004，40(2):746 －749.

［6］KIM S I，HONG J P，KIM Y K，et al.Optimal design of slotlesstype PMLSM considering multiple responses by response surface methodology［J］.IEEE Transactions on Magnetics，2006，42(4):1219－1222.

［7］秦世耀，熊光煜，牛华.永磁电机气隙磁场的解析分析［J］.太原理工大学学报，2002，33(2):121－124.QIN Shiyao，XIONG Guangyu，NIU Hua.Analysis of magnetic field in air gap due to permanent magnet motor［J］.Journal of Taiyuan University of Technology，2002，33(2):121－124.

［8］KANG G H，HONG J P，KIM G T.A novel design of an air-core type permanent magnet linear brushless motor by space harmonics field analysis［J］.IEEE Transactions on Magnetics，2001，37(5):3732－3736.

［9］JANG S M，YOU D J，LEE S H，et al.Design and analysis of three types for permanent magnet linear synchronous machine［C］//Sixth International Conference on Electrical Machines and Systems，November 9 －11，2003，Beijing，China.2003，1:31－33.

［10］汤蕴璆.电机内的电磁场［M］.北京:科学出版社，1981:48－79.