一类分数阶滤波器逼近阶次的选择

赵慧敏， 李文， 邓武

(大连交通大学 软件学院，辽宁 大连 116028)

0 引言

机车减振系统对列车的运行性能、乘车舒适度等方面起着重要的作用。然而，也正是由于减振降噪措施的引入，不可避免地使牵引电机传动系统变得更加复杂。例如，由于减振材料或装置的粘弹性或耗能特性，系统的分数阶特性变得无法忽略。分数阶控制除了对复杂被控对象具有更好的控制特性和灵活的参数调节能力外，在交流电机振动抑制中也起着一定的积极作用［1－3］。因此，为提高牵引电机传动系统减振降噪性能，拓展传统的整数阶、确定性分析方法，研究牵引电机传动系统分数阶控制具有实际意义。

一个含有分数阶环节的系统称为分数阶系统，在建立或实现分数阶环节的过程中，分数阶算子通常是用一个整数阶多项式或有理分式来逼近的，其逼近精确度直接影响分数阶控制性能的优劣。为此，研究者们提出了多种分数阶算子的逼近方法，取得了越来越好的逼近效果［4］。然而，在这些研究中，对逼近精确度与逼近模型阶次之间关系的讨论却不多见。一般来说，逼近模型的阶次越高，逼近精确度就越高。但是，当阶次达到一定值后，逼近精确度的提高随阶次的提高不再明显，因此了解逼近精确度与逼近阶次之间的关系，对分数阶控制系统的实现有着具体的指导意义。

本文在讨论Oustaloup曲线拟合法［5］对分数阶滤波器进行有理分式逼近方法的基础上，对分数阶滤波器Qα(s)有理分式逼近阶次选择与逼近精确度之间的关系进行研究。对比不同分数阶次和不同逼近阶次下，逼近模型与理想模型的幅、相频率特性及其误差来观察逼近阶次与逼近精确度的关系，并由此来确定最佳逼近阶次。

1 分数阶滤波器

分数阶滤波器的特点是滤波器的阶次α可以在实数范围内选择，即α∈R。分数阶滤波器使得传统滤波器的阶次由分级可调(α只能取整数)变为连续可调(α可以取实数)。滤波器阶次的调节变得灵活和细腻，从而能够更好地满足系统设计要求，解决了传统干扰观测器在相角裕度损失和低频振动抑制能力之间的矛盾。

设一类分数阶低通滤波器为

由于任意一个实数总可以分为一个整数和一个小于等于1的实数之和的形式，故假设α∈［0，1］，式(1)对应的Bode图如图1所示。由图1可知，分数阶滤波器的Bode图曲线介于相邻的两个整数阶曲线之间，再一次说明了分数阶滤波器在阶次选择上具有更大的灵活性。

图1 分数阶Q滤波器Bode图Fig.1 Bode chart of fractional Q filter

在设计分数阶滤波器时，常数τ(或带宽ωq)和分数阶次α是2个重要参数。在实际应用中，带宽通常是可以事先确定的，因此，分数阶滤波器的设计就变成了对分数阶次α的确定问题。α参数是通过综合干扰抑制能力和鲁棒稳定性来具体确定的［6］。

2 分数阶微积分算子的逼近

当分数阶次α被综合确定后，分数阶滤波器的数字实现即分数阶滤波器的离散化是需要考虑的主要问题。然而，分数阶滤波器是基于分数阶微积分运算的，与传统整数阶有很大的不同，需要采取一些特殊的方法来处理。

2.1 分数阶微积分算子离散化

分数阶微积分算子的离散化可分为直接离散化与间接离散化2种方法。直接离散化方法首先通过生成函数s=ω(z－1)对分数阶微积分算子s±r(r∈R)进行变换，在离散时间域Z中得到一个无理函数ω±r(z－1);之后，用一个有限阶次的有理函数对其进行逼近［7］。幂级数和连分式展开是在实现有理化处理时常用的方法。间接离散化方法包括2个步骤:一是建立与连续时间域相匹配的频域传递函数，其本质上是一个逼近或近似的过程;二是对所得到的S域传递函数进行离散化。研究表明，用多项式逼近某些函数的效果不如用有理函数逼近的效果好［8］;并且由于连分式展开法并不能确保离散化模型能保持原分数阶模型的稳定性，且在实现精确度上不是很理想［9］，多采用有理函数逼近的方法来实现。有理函数逼近方法有很多优点，如可以对未知的信号进行分数阶微积分等，它克服了连分式所带来的缺点，且逼近效果较好。A Oustloup等人分别提出了相应的方法［5］，取得了很好的逼近效果。

2.2 Oustaloup算法

Oustaloup算法［5］是在对复数阶次微分器的研究为基础得来的，对于复变传递函数 G(s)=，令β=0，去掉高、低频部分，选定拟合频率段为［ωb，ωh］，则复变传递函数可用一个频带有限制的传递函数来表示，为

式中:C0=ωb/ωu=ωu/ωh;ωu=(ωbωh)1/2。则式(2)又可改写为

式(3)是一个无理函数，Oustaloup算法采用有理函数级联的方式来实现对式(3)的逼近。级联的有理函数为

式(4)可以看作一个IIR型滤波器，其阶次n=2N+1，且n越大逼近精确度越高。以分数阶微分s0.5为例，简要说明Oustaloup算法的基本思想。设ωb=0.01 rad/s，ωh=100 rad/s，当 N=0，1，2，即滤波器阶次n(在此又称逼近阶次)分别为1，3，5时，对应的IIR滤波器传递函数表达式分别为

式(6)～式(8)对应的幅频特性和相频特性如图2所示。由图2可以看出，在设定频段内，不同逼近阶次对分数阶微分算子s0.5的逼近效果。

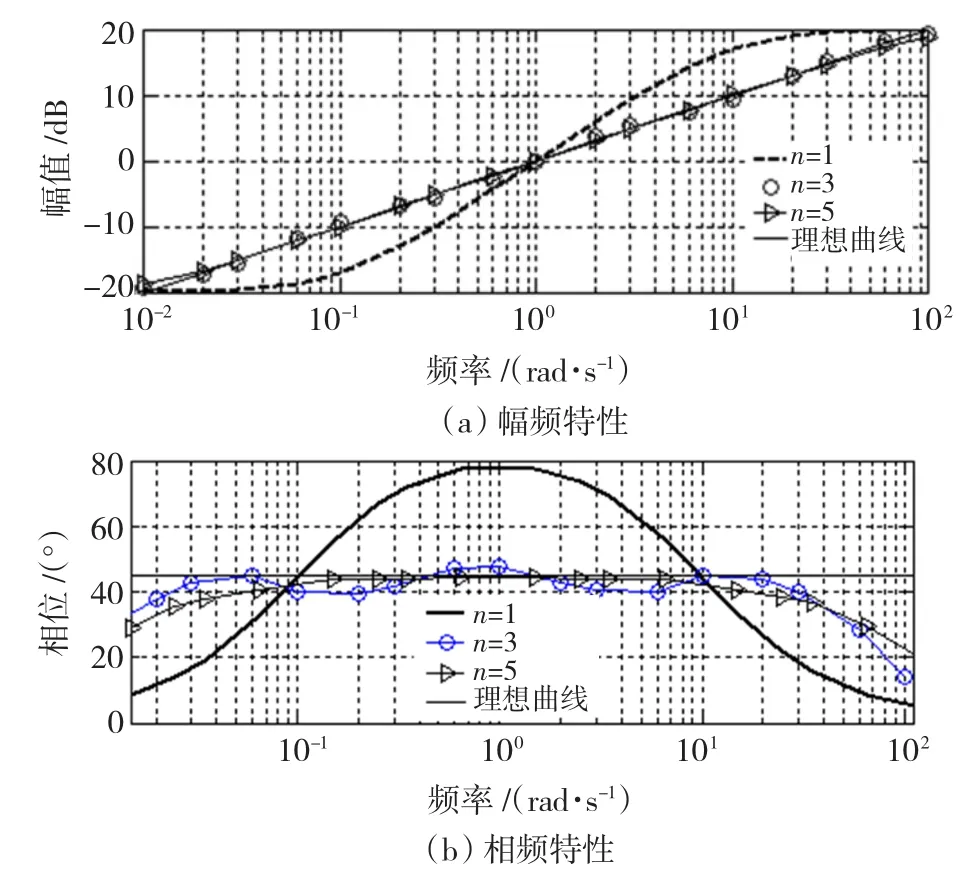
图2 不同逼近阶次下的特性比较Fig.2 Comparison of property under different approximation order

当逼近阶次n=1时，逼近误差很大，当逼近阶次n=5时，无论幅频特性还是相位特性都能较好地逼近s0.5的特性。从理论上讲，逼近阶次n越高，逼近精确度就越高。但当阶次达到某一值后，逼近精确度与逼近阶次不再成比例提高，过高的逼近阶次在实际中是没有意义的，应折中考虑逼近精确度与系统综合性能的关系。

2.3 逼近阶次的选择

设所要实现的分数阶低通滤波器Qα(s)对应的传递函数为

对式(9)运用Oustaloup算法进行有理函数逼近处理。设逼近频段为［ωb，ωh］，取ωb=式(9)可以表示为

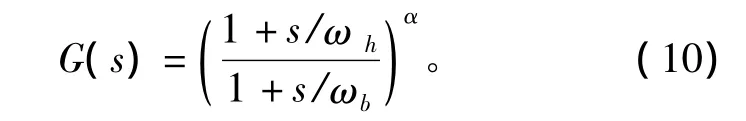
式(10)是一个无理函数，用一个有理函数级联的方式来实现对式(10)的逼近，为

则式(5)变化为

式(11)给出的有理分式逼近模型的阶次n(亦即IIR型滤波器的阶次)对逼近效果有很大的影响［6］。

设在频段［100，10000］内进行逼近，分数阶次α =0.2，0.4，0.6，0.8，逼近阶次 n=1，3，5，7。通过计算逼近模型与式(9)的幅、相频率特性及其误差来观察逼近阶次n与逼近精确度的关系，来确定最佳逼近阶次。

幅频特性误差与相频特性误差分别为

对不同分数阶次α和逼近模型阶次n，利用Matlab进行编程，可以得到对数幅、相频率特性曲线如图3(a)、图4(a)、图5(a)、图6(a)所示。不同分数阶次及逼近阶次情况下，幅频特性和相频特性的逼近误差可由式(13)和式(14)计算得到，对应的误差曲线如图3(b)、图4(b)、图5(b)、图6(b)所示。图3～图6的频率特性及逼近误差曲线的比较表明，当逼近阶次n=5时，对不同的分数阶次α，无论是幅频特性，还是相频特性都能很好地逼近实际分数阶滤波器的频率特性。

表1和表2分别给出了在不同分数阶次α和逼近阶次n下，有理分式逼近模型式(11)的幅、相频特性曲线与实际分数阶滤波器式(9)的幅、相频率特性在逼近频段内的绝对误差平均值，计算公式为

式中:ω0=ωb;ωH=ωh。

平均值越小说明逼近精确度越高。通过定量计算，进一步验证了当n=5时，幅频特性绝对误差平均值小于0.027 dB，相频特性绝对误差平均值小于0.16°，达到了比较满意的逼近效果。由表1和表2还可以看出，用于逼近分数阶滤波器的有理分式逼近模型的阶次n<5时，随着逼近阶次n的提高，幅、相频率特性的绝对误差平均值迅速减小，如图7所示。虽然n=7时误差也在减小，但其变化幅度已明显下降。随着逼近阶次的提高，系统的零、极点增多，增加了系统的复杂性，同时对系统性能、运算复杂性及实时控制等方面都会带来一些不利因素。因此，当采用式(11)来逼近具有式(9)形式的分数阶滤波器时，其最佳逼近阶次n为5。

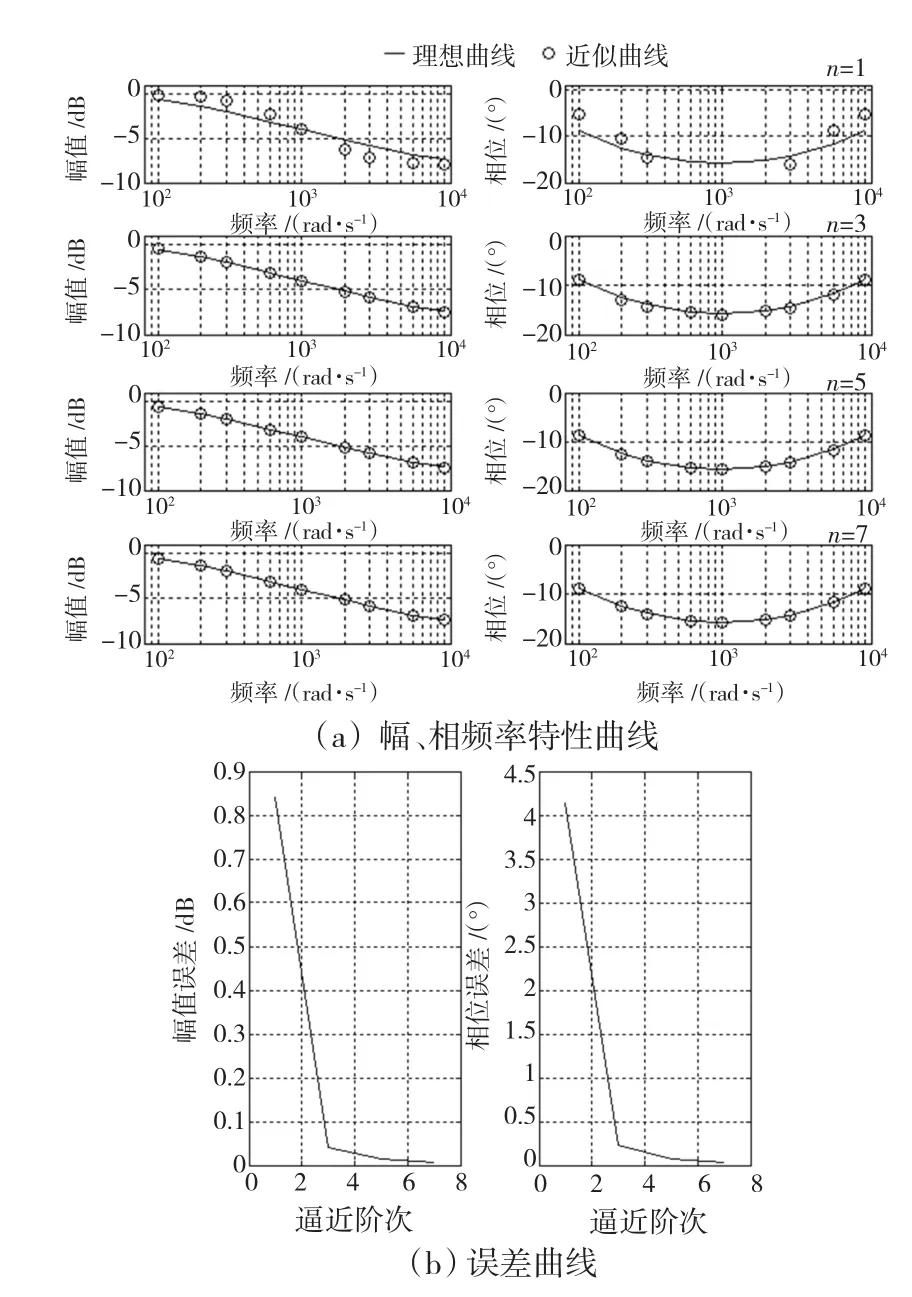
图3 当α=0.2，n=1，3，5，7时的幅、相频率特性曲线和误差曲线Fig.3 Amplitude-and-phase-frequency characteristic and error curve(α =0.2，n=1，3，5，7)

图4 当α=0.4，n=1，3，5，7时的幅、相频率特性曲线和误差曲线Fig.4 Amplitude-and-phase-frequency characteristic and error curve(α =0.4，n=1，3，5，7)

图5 当α=0.6，n=1，3，5，7时的幅、相频率特性曲线和误差曲线Fig.5 Amplitude-and-phase-frequency characteristic and error curve(α =0.6，n=1，3，5，7)

图6 当α=0.8，n=1，3，5，7时的幅、相频率特性曲线和误差曲线Fig.6 Amplitude-and-phase-frequency characteristic and error curve(α =0.8，n=1，3，5，7)

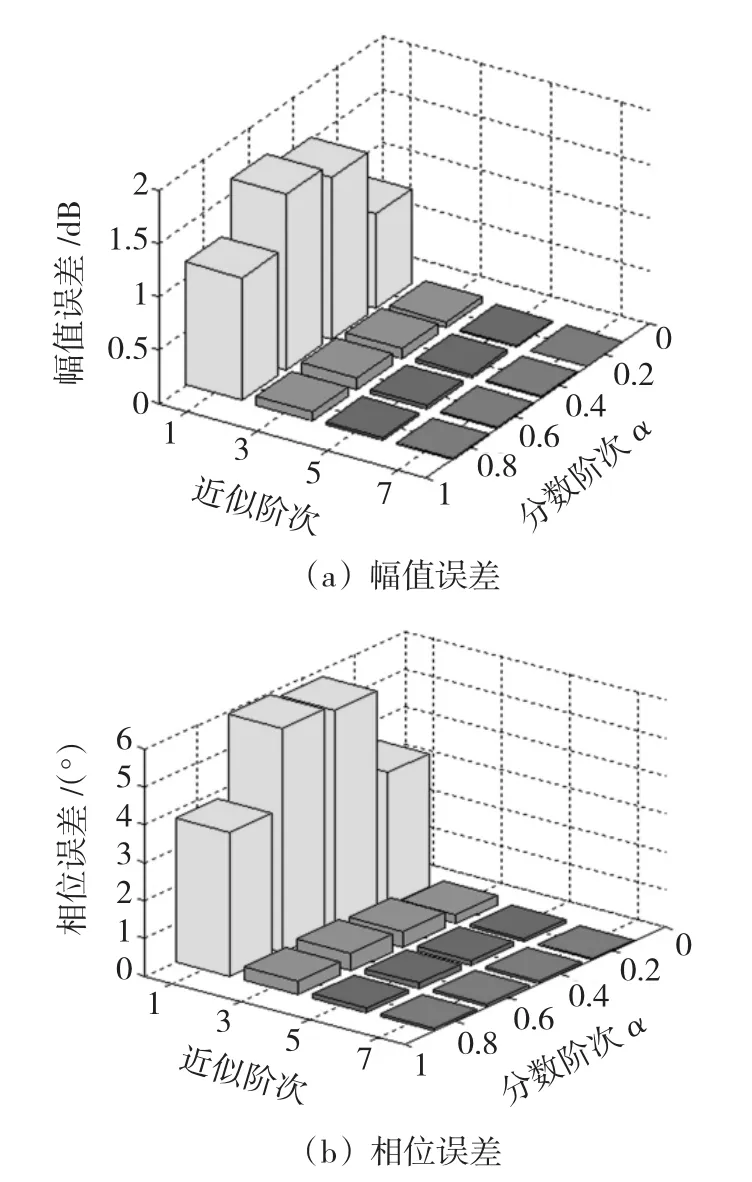
图7 随n和α变化的幅、相误差关系图Fig.7 Amplitude and phase error diagram changing with n and α

表1 逼近模型与实际分数阶滤波器幅频特性绝对误差平均值Table 1 The average of absolute error of amplitude-frequency characteristic of approximation model and practical fractional-order filters

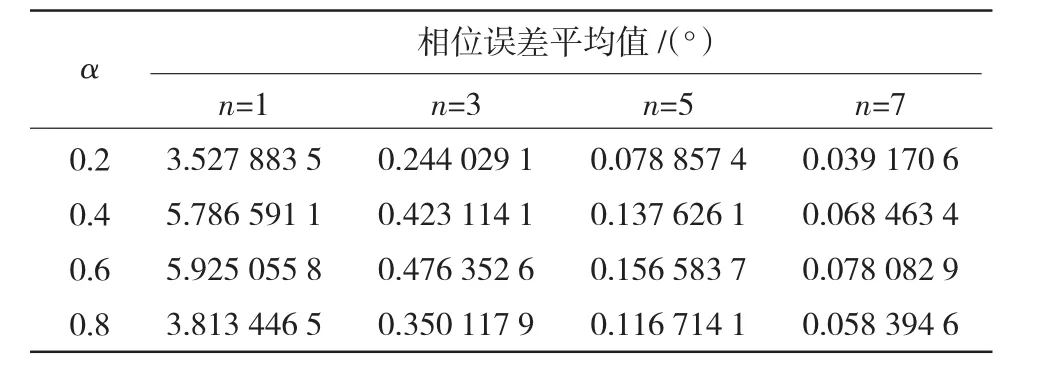
表2 逼近模型与实际分数阶滤波器相频特性绝对误差平均值Table 2 The average of absolute error of phase-frequency characteristic of approximation model and practical fractional-order filters

3 结语

通过对Oustaloup算法进行仿真分析及逼近误差计算，给出了在选定频段内，在不同分数阶阶次α及逼近阶次n情况下的幅、相频特性曲线，幅值、相位绝对误差平均值随α、n变化的柱状图。研究结果表明，在不同分数阶次α下，逼近模型的阶次n<5时，逼近误差随着逼近阶次的提高而迅速减小;当n>5后，误差随阶次提高而减小的程度明显下降。考虑到逼近阶次越高，引入的零、极点也越多、运算量也越大，不利于实时控制及系统特性改善，因此在应用Oustaloup算法对分数阶滤波器进行离散化时，其最佳的逼近阶次为5。

［1］MACHADO J A T.Analysis and design of fractional－order digital control systems［J］.Systems Analysis Model Simulation，1997，27(2/3):107－122.

［2］KOMADA S，MACHII N，HORI T.Control of redundant manipulators considering order of disturbance observer［J］.IEEE Transactions on Industrial Electronics，2000，47(2):413 －420.

［3］LEE H S，TOMIZUKA M.Robust motion control design for high accuracy position system［J］.IEEE Transactions on Industrial E-lectronics，1996，43(1):48 －55.

［4］LUBICH C.Discretized fractional calculus［J］.SIAM Journal on Mathematical Analysis，1986，17(3):704 －719.

［5］OUSTALOUP A，LEVRON F，MATHIEU B，et al.Frequencyband complex noninteger differentiator:characterization and synthesis［J］.IEEE Transactions on Circuit and Systems-I:Fundamental Theory and Applications，2000，47(1):25 －39.

［6］樊玉华.分数阶干扰观测器研究［D］.大连:大连交通大学电气信息学院，2007:33－45.

［7］CHEN Yangquan.A new discretization method for fractional order differentiators via continued fraction expansion［C］//2003 ASME International Design Engineering Technical Conferences，September 2－6，2003，Chicago，USA.2003:1－9.

［8］NEWMAN D J.Rational approximation to|x|［J］.Michigan Mathematical Journal，1964(11):11 －14.

［9］王仁宏.有理函数逼近及其应用［M］.2版.北京:科学出版社，2004:116－129.