基于动态BP算法的非线性滞后系统辨识

韩 冰， 韩 敏

（1.大连理工大学 控制科学与工程学院，辽宁 大连 116024；2.上海船舶运输科学研究所，上海 200135）

0 引 言

系统辨识作为控制科学的核心问题长期以来一直受到广泛的关注.非线性系统，特别是包含滞后的非线性系统辨识一直是控制领域的难题之一[1].对非线性滞后系统的辨识，以往传统的方法是从输入输出数据入手，采用Hemmserstein模型[2]、Wiener模型[3]等模型结构进行建模.但对于结构和参数未知的系统，以上方法很难对实际系统进行表达.随着智能建模理论的发展，局部模型近似[4]、模糊模型[5]、支持向量机[6]以及遗传算法[7]等得到了广泛的采用，但这些方法对先验知识仍具有较强的依赖性.因此，如何对模型参数完全未知非线性滞后系统进行辨识，如何辨识得到该系统的延迟时间成为非线性滞后系统建模研究的关键问题.

对模型未知的滞后系统延迟时间辨识问题，Balestrino等[8]、陆燕等[9]提出了基于感知机神经网络进行延迟参数辨识的方法，但这些方法易受到网络参数和辨识对象等因素的影响，在实际应用中存在一定的局限.Ren等[10]扩展了延迟自由神经网络的思想，提出了可对一类滞后系统进行有效延迟参数估计的神经网络算法.Han等[11]在多分支延迟神经网络中引入可调的延迟参数，对包含滞后的非线性对象进行建模，并应用于预测控制中.这些研究成果表明，通过神经网络对模型未知的非线性滞后系统辨识是较为可行的方法.

本文利用神经网络具有很好的函数逼近能力，结合多层感知机网络的特点，分别在多层感知机网络的第1隐层和输出层引入带有自适应延迟参数的动态神经元，提出一种包含动态特性的动态BP学习算法.该算法对于黑箱非线性滞后系统，能够通过第1隐层延迟参数来自适应选择模型输入变量，避免采用非线性含输入自回归（NARX）等建模方法进行输入变量选择时所需要的复杂计算[12].

1 动态BP算法

为了改善传统BP算法不具备动态特性的缺陷，本文在传统感知机神经网络的第1隐层和输出层引入动态神经元，构成新的动态BP神经网络.动态BP神经网络的结构如图1所示.其结构与传统BP神经网络相似，但在第1隐层和输出层引入了和网络权值对应的延迟参数.

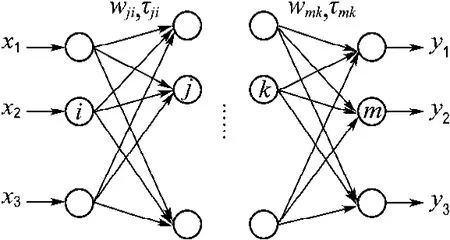
图1 动态BP神经网络结构图Fig.1 Basic structure of dynamic BP neural network

第1隐层和输出层的动态神经元输入如下式所示：

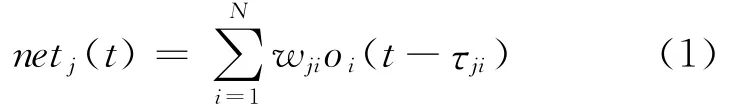
式中：net j（t）表示第j个动态神经元的输入；w ji表示前一层第i个神经元到该层第j个神经元之间的权值；oi表示该神经元的第i个输入，共有N个输入；τji表示前一层第i个神经元到该层第j个神经元之间的延迟参数.

动态神经元的输出为

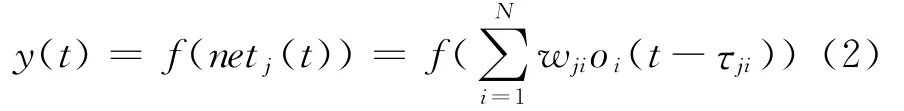
这里f为神经元激活函数，本文神经元激活函数均选取Sigmoid函数，如下式所示：

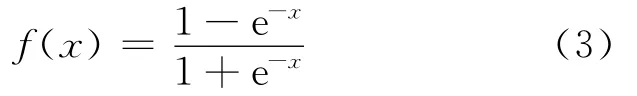
网络学习过程中，网络的权值可按传统BP算法[13]进行更新.网络误差函数为

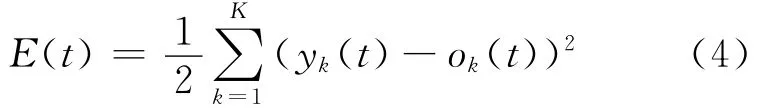
第1隐层和输出层的延迟参数可根据网络学习误差的梯度进行实时调整.对输出层的延迟参数，网络误差函数的梯度下降方法可给出延迟参数更新值为

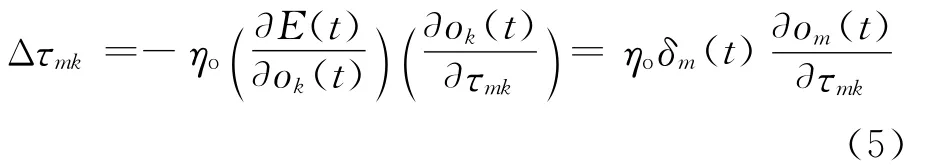
其中Δτmk为网络输出层第m个神经元与之前一层的第k个神经元之间延迟参数τmk的修正量，ηo为网络输出层延迟参数的学习率，om（t）为网络输出层第m个节点的输出，δm（t）为t时刻网络的学习误差，即

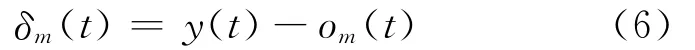
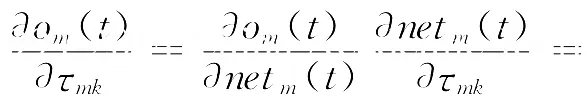
其中

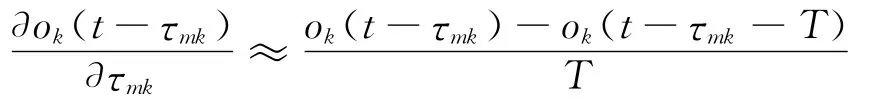
f为神经元激活函数，T为系统采样时间.

对第1隐层延迟参数，可按下式进行迭代更新：

式中：Δτji为网络输入层第i个神经元与第1隐层的第j个神经元之间延迟参数的修正量，ηi为网络第1隐层延迟参数的学习率，oj（t）为网络第1隐层第j个节点的输出，其中

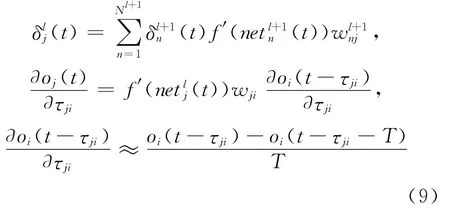
式中：（t）表示l层t时刻误差函数，第1隐层误差函数可由式（9）通过输出层误差递推得到.N l＋1表示网络第l＋1层的节点数；netln＋1（t）表示l＋1层网络第n个节点t时刻的输入；oi（t）表示神经网络的输入.

2 基于动态BP算法的系统辨识

一般的非线性系统可以表示为

其中N、M是最大的延迟范围.利用动态BP算法对系统（10）进行建模，使神经网络逼近系统（10）中的非线性函数f[·].由动态神经元输入式（1）可以将第1隐层的第j个神经元输出表示为

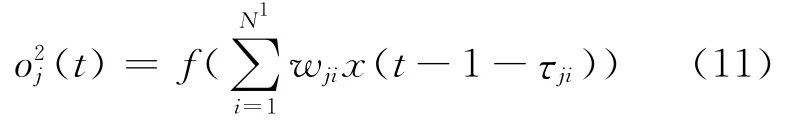
其中N1为网络第1层神经元个数，x（t－1－τji）为神经元的输入.将第2层的输出式（11）代入到第3层的计算中有

其中延迟参数τji通过使网络误差函数

最小化进行修正，这样经过层层迭代后，网络的输出可以表示为

其中L表示网络输出层，N[·]为神经网络所建立的非线性函数，τmax是所有延迟参数在训练结束后的最大值.训练过程中将前一时刻的输出y（t－1）作为输入，则网络的输出可以表示为

其中Nτ、Mτ是可能的最大延迟.从以上表达式可以看出，引入动态神经元使多层感知机网络具有了动态特性，能够对一类包含滞后特性的非线性对象进行建模.同时，从式（10）和（13）可以看出，通过辨识得到的神经网络延迟参数可以对滞后对象的延迟进行估计，从而为滞后对象的延迟时间辨识提供新方法.

3 仿真实例

利用本文提出的动态BP算法，分别对理论数学模型和实际生产过程进行系统辨识仿真，进而验证该算法的有效性.

3.1 大滞后模型辨识仿真实验

利用文献[14]中给出的动态模型来检验自适应算法的有效性.模型的差分方程如下：

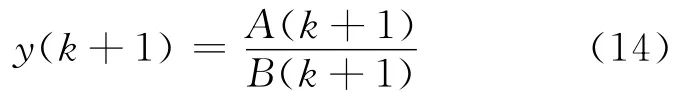
式中

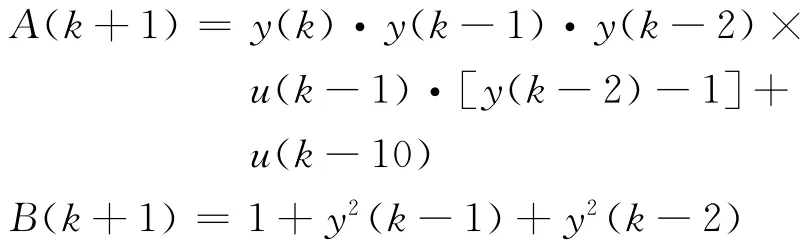
从模型的方程来看，当前的输出由先前的输出和输入决定，相对输入有10个单位的延迟.用于训练的教师信号由1000组输入输出序列组成.其中前500组用于训练网络，后500组用来检验网络泛化能力.输入为

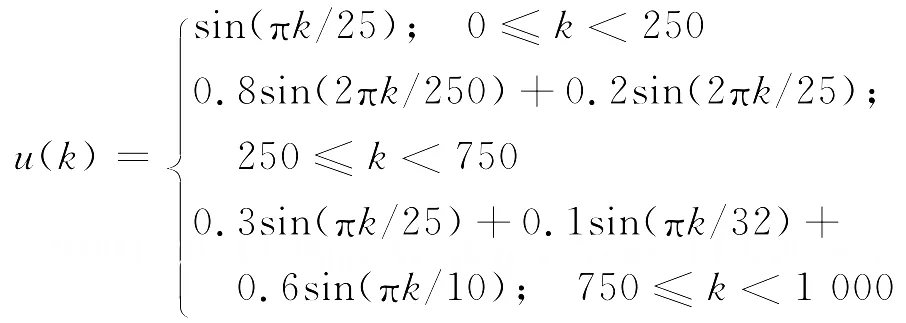
由u（k）产生的教师信号如图2所示.

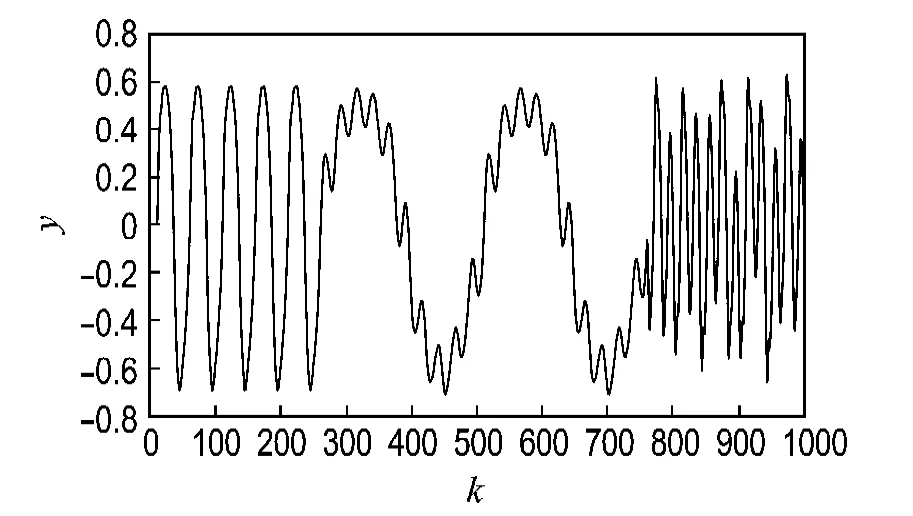
图2 网络学习和测试信号Fig.2 Learning and test signal of the network

利用C语言编程实现本文所提出的动态BP学习算法对该模型的辨识，仿真条件如表1所示.网络中共有45个延迟变量参数，第1隐层和输出层初始延迟值分别设置为1和12.经过20000次学习之后网络的学习误差和泛化误差分别为0.003030、0.005038，训练后网络的输出与教师信号的比较如图3所示.从图3中可以看出，训练后的动态BP网络很好地体现了非线性系统的动态特性.训练结束后，第1隐层延迟时间参数共10个值为1，其余20个延迟参数为0；输出层共6个延迟参数为10，其余9个值为9，可见输出层的延迟参数对辨识对象的纯滞后时间有较好的辨识能力.

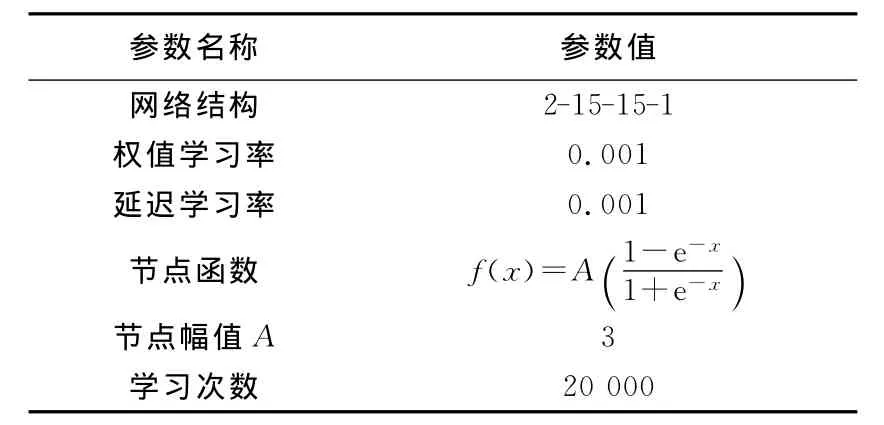
表1 仿真条件Tab.1 Simulation conditions

图3 泛化信号同教师信号的比较Fig.3 Comparison between generalizing signal and teacher signal

为验证引入自适应延迟参数在算法学习过程中的作用，采用传统BP算法与本文提出的引入延迟参数的动态BP算法进行比较.利用相同的网络结构采用传统BP算法经过20000次学习后得到的学习误差和泛化误差分别为0.003712、0.009019.通过误差的比较可以看出，引入了自适应延迟参数加快了网络的收敛速度，并且网络模型的泛化能力有了较大的提高，网络具有更好的表达系统动态特性的能力.

3.2 大滞后模型辨识仿真实验实例验证

为验证本文所提出的动态BP网络对实际工业生产过程建模的有效性，选取某炼油厂连续重整装置的芳烃抽提塔为建模对象.其中，溶剂比（环烃砜与进料量之比）作为可操作的控制量，抽提塔底温度为控制系统的输出变量.现场采集用于训练神经网络的信号如图4所示.其中虚线表示输入变量溶剂比a随时间的变化情况，其基值为3.25；实线表示抽提塔底温度θ的变化情况，其基值为172℃.系统采样时间为2 min，共100组数据，前90组数据用于训练网络，后10组数据用于检验网络的泛化能力.

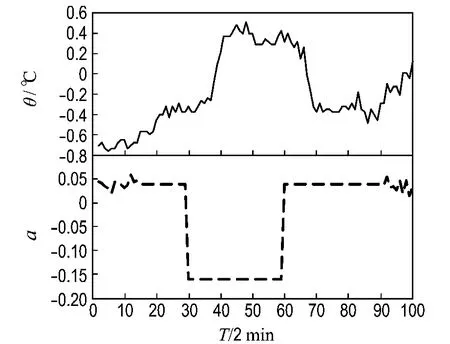
图4 网络学习和测试信号（实例）Fig.4 Learning and text signal of the network（example）

采用本文所提出的自适应选择延迟时间的学习算法对该模型进行辨识，仿真条件如表2所示.从图4可以看出，输出对阶跃响应的延迟在10个采样时间以内，因此将与输出节点相连的分支上的延迟时间初始值设为10.

网络共60个延迟变量参数，第1隐层初始延迟值分别设置为1.经过自适应选择，第1隐层延迟时间参数共10个值为1，其余延迟参数为0；输出层共12个延迟参数为8，其余8个为9，因此可认为该系统的滞后时间约为16 min.经过15000次学习之后，网络的训练误差为0.017534，泛化误差为0.020824.图5给出了神经网络的输出同样本信号的对比曲线，从图中可以看出神经网络能表现出实际系统的幅值特性和延迟特性，能够对抽提塔底温度的变化进行实时预报.本文所研究的方法为通过溶剂比调整抽提塔底温度提供了依据.

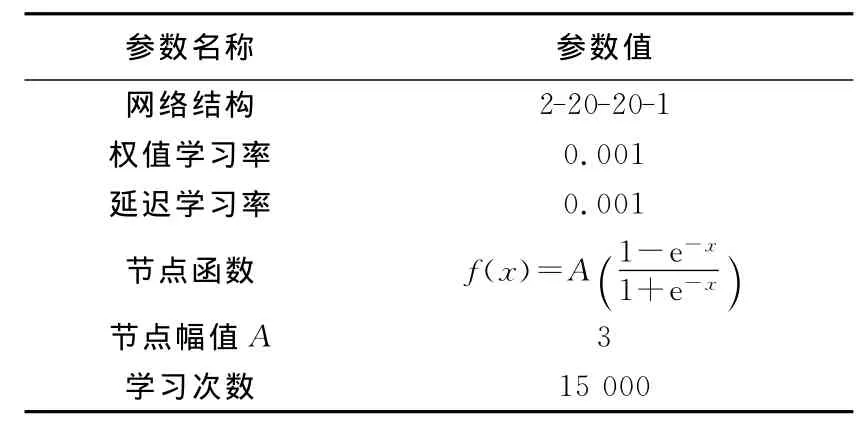
表2 仿真条件（实例）Tab.2 Simulation conditions（example）

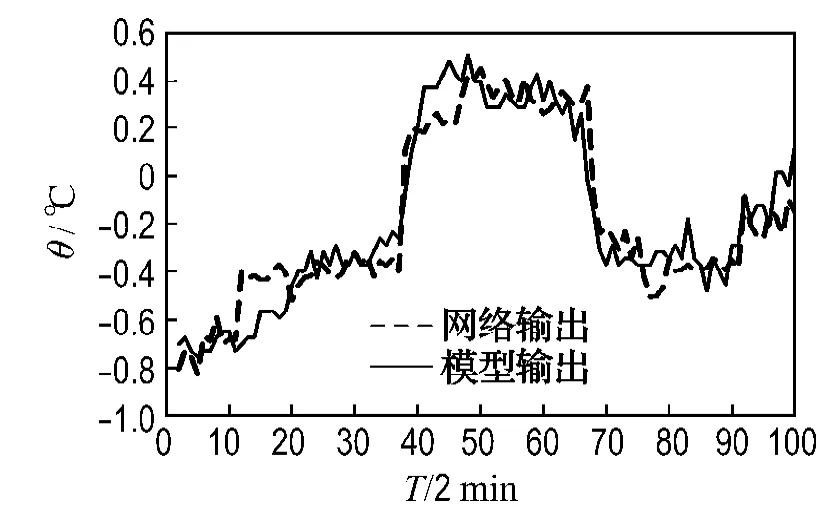
图5 泛化信号同教师信号的比较（实例）Fig.5 Comparison between generalizing signal andteacher signal（example）

在仿真实验过程中，延迟时间的初值设定会对网络的学习效果有一定的影响.因为在训练过程中，延迟时间参数学习率过大必然会导致延迟参数的调整频繁，会影响到系统的稳定性；而延迟时间参数过小会使网络学习效率降低，不能实现对被辨识对象延迟时间估计的作用.一般可将输入层延迟时间参数的初始值设置为1，输出层的延迟时间参数与被辨识对象的纯滞后时间相接近.对于未知对象的辨识，可以粗略估计其延迟时间来进行网络参数的设置.

4 结 语

本文针对包含滞后的动态非线性系统辨识的要求和特点，提出了可以自适应选择网络延迟时间参数的动态BP算法.该学习算法能够利用一个简单的网络结构在缺少先验知识的情况下，实现对非线性动态系统的建模.仿真结果表明：本文提出的动态BP网络能够很好地体现动态非线性系统的特性；能够根据网络的误差梯度对网络的延迟时间参数进行修正并且有利于网络精度的提高；最终辨识得到的网络延迟时间能够用于辨识对象的纯滞后时间.仿真实例证明本文所提出的动态BP网络改进算法为模型参数未知的非线性滞后系统辨识研究提供了新方法.

[1]GOMEZ O，OROLOV Y，KOLMANOVSKY I V.On－line identification of SISO linear time－invariant delay system from output measurements [J].Automatica，2007，43（12）：2060－2069

[2]PEARSON R K.Outliers in process modeling and identification [J].IEEE Transactions on Control Systems Technology，2002，10（1）：55－63

[3]GMEZ J C，JUTAN A，BAEYENS E.Wiener model identification and predictive control of a p H neutralisation process [J].IEE Proceedings－Control Theory and Applications，2001，151（3）：329－338

[4]王 蓬，李少远.一类非线性系统的多模型预测控制[J].控制与决策，2007，22（10）：1113－1118

[5]邢宗义，胡维礼，贾利民.基于T－S模型的模糊预测控制研究[J].控制与决策，2005，20（5）：495－499

[6]张日东，王树青.基于支持向量机的一类非线性系统预测控制[J].控制与决策，2007，22（10）：1103－1107

[7]ABBAS H M，BAYOUMI M M.Volterra－system identification using adaptive real－coded genetic algorithm [J].IEEE Transactions on Systems，Man and Cybernetics — Part A：Systems and Humans，2006，36（4）：671－684

[8]BALESTRINO A，VERONA F B，LANDI A.On－line process estimation by ANNs and Smith controller dedign[J].IEE Proceedings－Control Theory and Applications，1998，145（2）：231－235

[9]陆 燕，杜继宏，李春文.延迟时间未知的延迟系统神经网络补偿控制[J].清华大学学报（自然科学版），1998，38（9）：67－69

[10]REN X M，RAD A B.Identification of nonlinear systems with unknown time delay based on time－delay neural networks[J].IEEE Transactions on Neural Networks，2007，18（5）：1536－1541

[11]HAN M，HAN B，GUO W.Process control of p H neutralization based on adaptive algorithm of universal learning network [J].Journal of Process Control，2006，16（1）：1－7

[12]邢建国，许沧粟，孙优贤.发动机怠速控制NARX模型及辨识[J].内燃机工程，2002，23（1）：69－74

[13]SIMON H.Neural Networks：A Comprehensive Foundation [M].2nd ed.Canada：Prentice Hall，1999：162－167

[14]MASTOROCOSTAS P A，THEOCHARIS J B.A recurrent fuzzy－neural model for dynamic system identification [J].IEEE Transactions on Systems，Man and Cybernetics— Part B：Cybernetics，2002，32（2）：176－189