随机利率下增额两全保险

王 丽 燕， 郝 亚 丽， 张 海 娇， 杨 德 礼

（1.大连大学 信息工程学院，辽宁 大连 116622；2.中央财经大学 国际经济与贸易学院，北京 102206；3.大连理工大学 管理学院，辽宁 大连 116024）

0 引 言

寿险中的利率随机性问题，在近年来的保险精算研究中逐步得到人们的关注.对保险公司来说，利率随机性产生的风险是相当大的.随着精算理论研究的深入，利率风险吸引了越来越多的学者从事利率随机性的研究.

1971年，Polland首次把利息力视为随机变量，对精算函数进行了研究，其后一批学者开始采用各种随机模型来模拟随机利率.1976年，Boyel考虑了寿险与年金中死亡率与利率均为随机的情况，即所谓的“双随机性”；随后，Panjer和Bellhouse、Giaccotto、Dhaene、Hürlimann等有过这方面的研究.对于随机利率，他们都是以时间序列方法建模的，例如白噪声过程、AR（2）过程和ARIMA过程等[1].20世纪90年代，一批学者利用摄动方法建模，得到了具有“双随机性”的确定年金及寿险的一系列结果：Beekman等[2、3]分别将息力累积函数用O－U过程和 Wiener过程建模，得到某些年金现值的前二阶矩；1993年他们又得到了息力由O－U过程和Wiener过程建模的终身寿险给付现值的前二阶矩[4].De Schepper等[5～7]得到了息力由 Wiener过程建模的某些年金的矩母函数、分布函数和Laplace变换.何文炯等[8]对随机利率采用Gauss过程建模，得到了一类即时给付增额寿险的给付现值的各阶矩，并在死亡均匀分布假设下，得到了矩的简洁表达式.刘凌云等[9]则将息力采用Gauss过程和Poisson过程联合建模，也给出了一类即时给付增额寿险给付现值的各阶矩，发展了文献[8]的结果.以上都是将利息力采用息力累积函数i（t）＝δt＋z（t）建模，其中δ是与z（t）无关的随机变量或实常数.与此相联系的问题是z（t）将可能变成负的.但实际上，保费收入一般投资于基金和债券，所以z（t）绝不可能是负的.Perry等[10、11]将随机利率采用反射 Brownian运动（RBM）建模，得到确定年金的期望值公式.Zaks也将随机利率采用反射Brownian运动建模，讨论了确定年金的计算问题[12].无论是Wiener过程、Gauss过程还是反射Brownian运动，它们都是处处连续的扩散过程，但现实的随机利率是不频繁却又在某些点离散跳跃的过程.随机跳跃是因突发事件对利率产生了影响，因此利率的动态过程分为连续部分和跳跃部分.Ngwira等[13]讨论了养老金在随机环境下的泊松跳跃问题，研究结果表明平均泊松跳跃的增加减少了风险资产的分配，并增加了无风险资产的分配.

本文在上述研究工作的基础上，建立一个具有储蓄功能的生死两全保险模型，模型中引入增额生存年金、增额终身寿险以及储蓄还本部分.考虑到保费的实际投资情况和突发事件对利率的影响，用反射Brownian运动来描述随机利率的连续变化部分，而用Poisson跳跃过程来描述不可预测的随机事件对利率连续性的破坏.将随机利率采用反射Brownian运动和Poisson过程联合建模.给出保单全部价值的计算公式，并进一步得到死亡均匀分布时的简洁计算公式.

1 准备知识

以X记被保险人在死亡时的年龄，则X是一个随机变量，以F（x）记X的分布函数，则

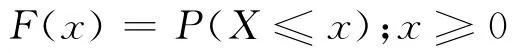
s（x）＝1－F（x），称为生存函数.用（x）表示年龄为x岁的人，也称x岁生命，X为（x）的寿命，用T（x）表示其剩余寿命，T（x）＝X－x，则T（x）的密度函数为

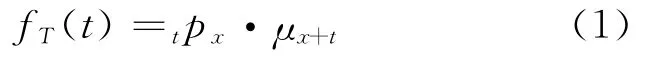
其中tpx表示（x）至少活到x＋t岁的概率；某生命在瞬间的死亡概率表示（x）在年龄x＋t处的死亡力.

2 模型的建立

设被保险人现龄x岁，身体健康，每年交保费m次，每次R元（期初交付），交款至n岁（x＜n）.本文在不考虑税收情况下讨论生死两全保险.

2.1 保险责任

（1）增额寿险部分：无论（x）何时死亡，都在死亡时即刻赔付保险金A（1＋α[T]）元，其中A＞0为确定的常数，α＞0为增长系数，[T]为被保险人整值剩余寿命.

（2）增额年金部分：如果被保险人生存至h（h≥n）岁，则h岁以后每年可一次性领取生存保险金B[1＋（k－h）l]元，直至死亡，其中B＞0为确定的常数，l＞0为增长系数，k＝h，h＋1，…，[T].

（3）储蓄还本部分：当被保险人去世时，退还至死所交保费的C倍（C＞0为确定的常数）.

2.2 保费的计算

首先计算出保险公司收入和支出的各项有关现值的数学期望，即精算现值，列出平衡方程，即可求出均衡年保费R的值.息力累积函数采用反射Brownian运动和Poisson过程联合建模，即

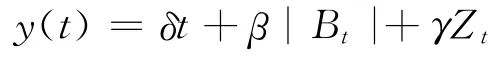
其中｜Bt｜是反射Brownian运动，Zt是Poisson过程，Bt与Zt相互独立且均与T（x）独立，δ、β、γ是与t无关的随机变量或实常数且均与Bt、Zt独立.

设投保人每次交保费R元，一年交m次，连续交保费n－x年.若每次交付1个单位的保额，则其现值为e－y（k），k＝0，1，…，n－x－1.以¨an－x表示其精算现值，则共缴纯保费mRa¨n－x，其中

因Zt是参数为λ的Poisson过程，所以

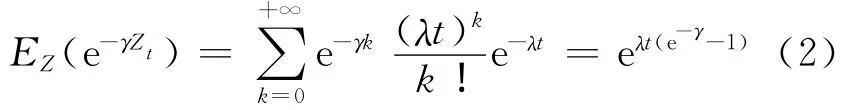
由反射Brownian运动的定义，有

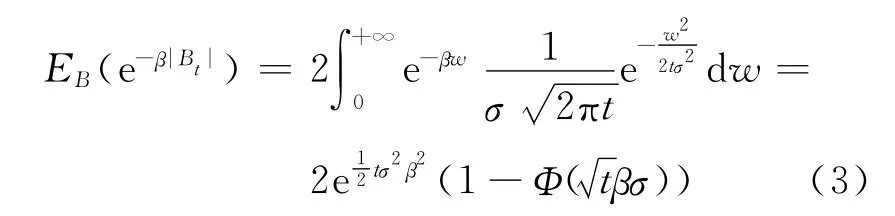
从而

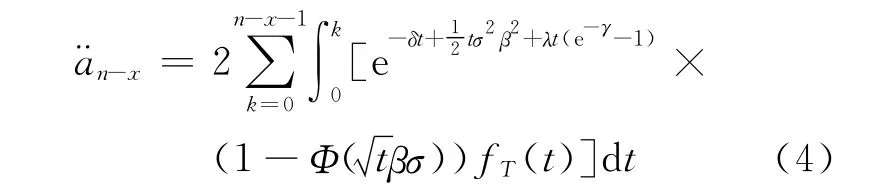
2.3 保单价值的计算

2.3.1 增额寿险部分 如果（x）在x＋t岁时死亡，得到的赔付额为1＋α[T]，则其现值为（1＋α[T]）e－y（T），若用Ax表示其精算现值，则

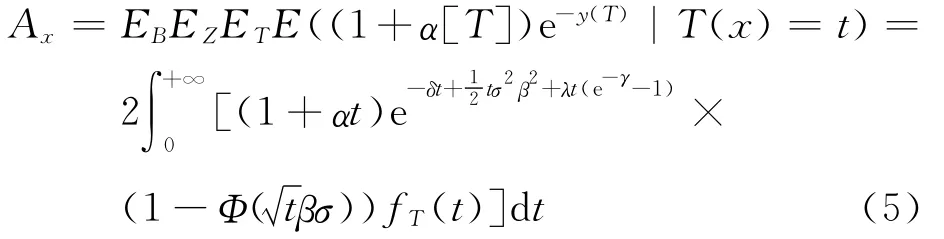
从而增额寿险的精算现值为AAx元.显然，当α＝0时，增额寿险变成了等额寿险.

2.3.2 增额年金部分 若被保险人（x）生存至h岁以后，第k年可获得保险公司支付的1＋（kh）l个单位的年金，则其现值为[1＋（kh）l]e－y（k），以表示其精算现值，则

式中：qx＋k表示（x＋k）在1 a内死亡的概率.

2.3.3 储蓄还本部分 设被保险人死亡时所得到的返回部分是1个单位，则其现值为随机变量e－y（t），记其精算现值为E（Y），则

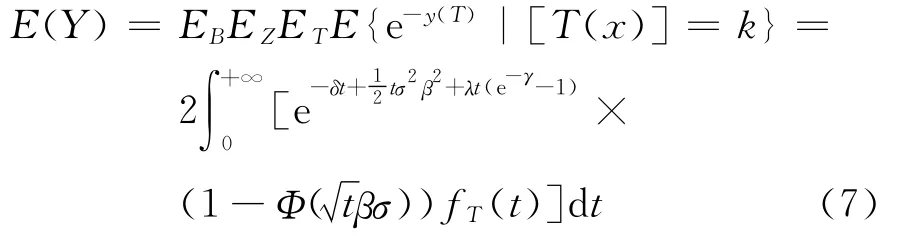
根据平衡原则，得到平衡方程

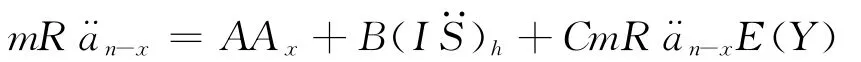
由平衡方程可以计算出每次所交保费

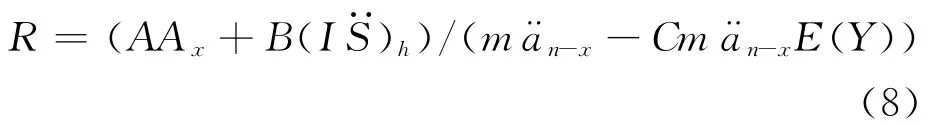
如果在每一保单年度内死亡是均匀发生的，将保险期［0，n）分成n等份， 则在每一［k，k＋1）上，T服从均匀分布，在这种情况下，对任意的t∈ ［k，k＋1），fT（t）＝tpx·qx＋k，于是式（1）变成

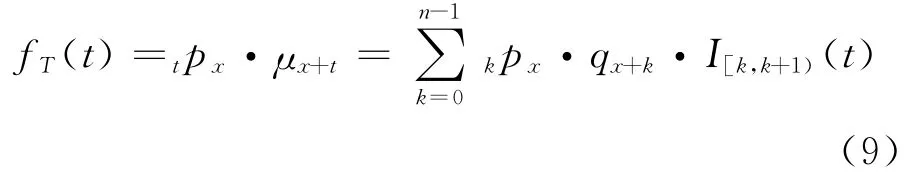
其中I［k，k＋1）（t）是示性函数.对由l0个新生生命组成的群体，在第x年还生存的人数为lx，则在第x年死亡的人数为dx＝lx－lx＋1，于是

并注意到

则在死亡均匀分布条件下，将式（9）～（11）代入到式（4）～ （7）中，有

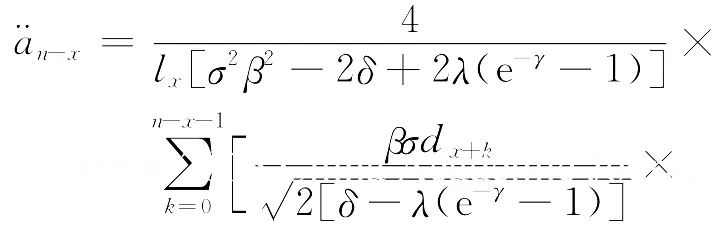
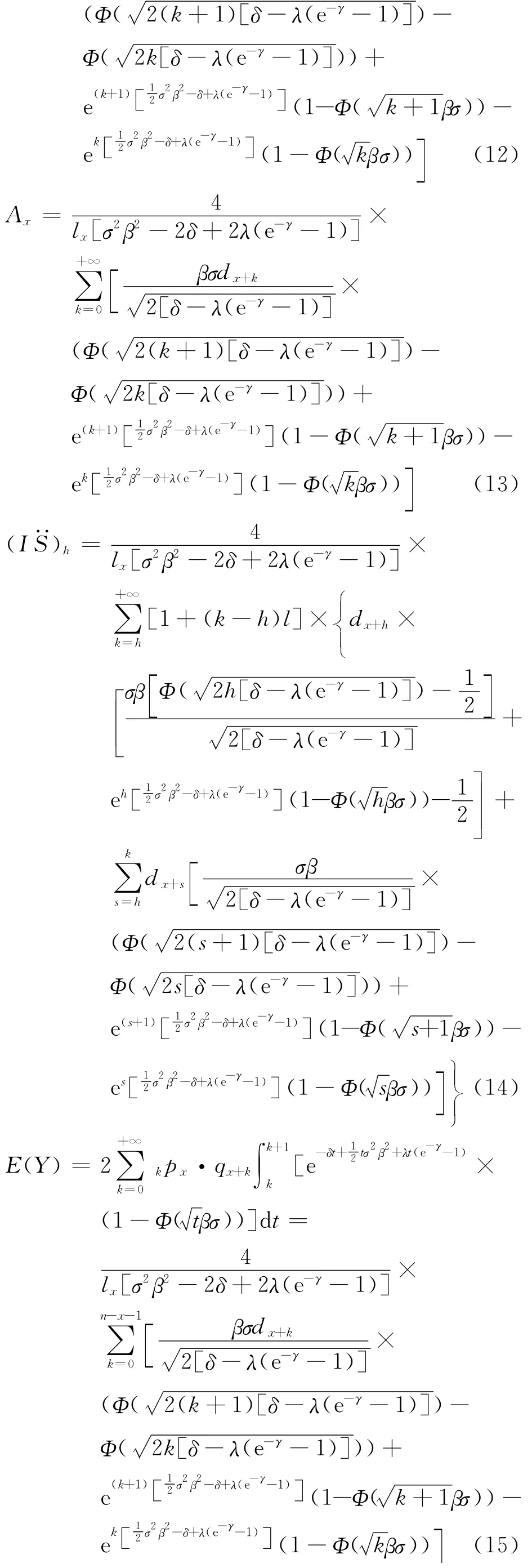
这样用生命表就可以简单地进行保费的计算了.

3 结 论

本文建立了一个新的寿险精算模型，模型中含有终身寿险、年金和还本部分，对于投保人来说，这种保险具有保险和储蓄的双重功能，增加了保险的吸引力.而且保险公司可以根据不同的情况调整参数得到不同的保险产品.本文还同时考虑了利率的随机性，在随机利率中引进Poisson过程，可以避免或减小突发事件所形成的利率风险对保险公司的影响；而引进反射Brownian运动，则避免了采用较高的固定利率计算保费给投保人造成的经济负担.模型充分考虑了投保人和保险公司的综合利益，最终使投保人和承保人都有所收获，可以确保保险经营的正常进行.

[1]伍超标.博士后研究工作报告《概率统计的若干应用问题》之4.4[R].上海：华东师范大学，1995：84－92

[2]BEEKMAN J A，FUELLING C P.Interest and mortality randomness in some annuities [J].Insurance：Mathematics and Economics，1990，9（2－3）：185－196

[3]BEEKMAN J A， FUELLING C P. Extra randomness in certain annuity models[J].Insurance：Mathematics and Economics，1991，10（4）：275－287

[4]BEEKMAN J A，FUELLING C P.One approach to dual randomness in life insurance[J].Scandinavian Actuarial Journal，1993，76（2）：173－182

[5]DE SCHEPPER A，DE VYLDER F，GOOVAERTS M，etal.Interest randomness in annuities certain[J].Insurance：Mathematics and Economics，1992，11（4）：271－282

[6]DE SCHEPPER A，GOOVAERTS M.Some further results on annuities certain with random interest[J].Insurance：Mathematics and Economics，1992，11（4）：283－290

[7]DE SCHEPPER A，GOOVAERTS M，DELBAEN F.The Laplace transform of annuities certain with exponential time distribution [J]. Insurance：Mathematics and Economics，1992，11（4）：291－294

[8]何文炯，蒋庆荣.随机利率下的增额寿险 [J].高校应用数学学报 A辑（中文版），1998，13（2）：145－152

[9]刘凌云，汪荣明.一类随机利率下的增额寿险 [J].应用概率统计，2001，17（3）：283－290

[10]PERRY D，STADJE W.Function space integration for annuities [J].Insurance：Mathematics and Economics，2001，29（1）：73－82

[11]PERRY D，STADJE W，YOSEF R.Annuities with controlled random interest rates [J].Insurance：Mathematics and Economics，2003，32（2）：245－253

[12]ZAKS A.Annuities under random rates of interest[J].Insurance：Mathematics and Economics，2001，28（1）：1－11

[13]NGWIRA B，GERRARD R.Stochastic pension fund control in the presence of Poisson Jumps[J].Insurance：Mathematics and Economics，2007，40（2）：283－292