Copula方法在时间序列趋势项提取中应用

2010-06-05赵越，宋立新，回德俊

大连理工大学学报 2010年5期

赵越，宋立新，回德俊

（大连理工大学数学科学学院，辽宁大连 116024）

0 引言

时间序列分析方法是生产和实际中经常用到的研究手段，在经济、气象和水利等领域有着广泛的应用.本文所要研究的对象是非线性随机序列，是指从非线性系统获取的时间序列.当系统具有混沌特征时，前人已论证了对非线性时间序列采用动力系统方法进行预测比较有效[1].实际上，通过观测或实验获得的时间序列往往含有噪声，也可能不平稳，需要进行降噪处理，对含有随机因素影响的原始观测序列提取趋势项.常用的趋势项提取方法有最小二乘法、平均斜率法和最佳拟合广义多项式等方法，这些方法经常用在信号处理、检测技术等工程中[2、3].本文在趋势项提取的判断标准上引入一种新的衡量准则，即基于Copula方法构造积分绝对误差函数，以此来判断不同方法所提取的趋势项合理性.最后将动力系统[1]建立在所提取的趋势项数据基础之上，针对次贷危机以来美国证券市场实际数据进行模拟和预测.

1 衡量模型构造

在实践中可以得到容量为n的一组时间序列观测值，同样对该样本序列进行类似的分解，记为.应用不同提取趋势项的方法，可得到不同的估计，记为面对多组估计，要找到最接近真实的一组，思路如下：由在得到一组估计值后，将残差作为的估计值，若它是最接近正态分布N（0，Σ）的残差向量，其所对应的即是要找的趋势项的最优估计.通过Copula函数，构造了一个衡量模型来衡量积分绝对误差，目标完成.具体过程如下：对于任意的（u，v）∈I2＝ [0，1]2，由Sklar定理，可构造二元Copula函数，记为CΣ（u，v）[4].设，其中，规定这里σ0为大于0的常数.此时函数可写为

式中：Nρ是二元正态分布函数，F（·）和G（·）分别为边缘分布函数，Σ中σ1、σ2和相关系数ρ都是未知的.

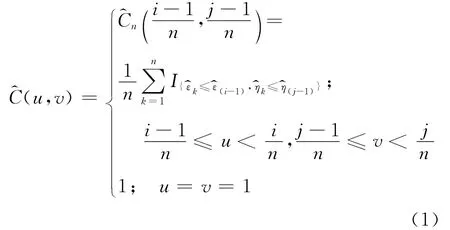
记的秩为的秩为.则式（1）改写为

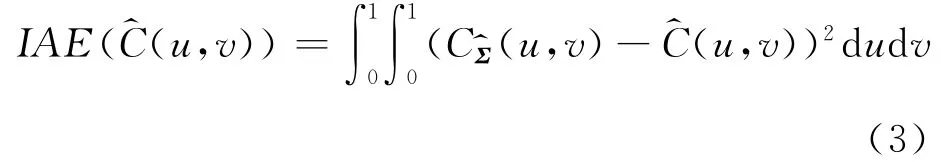
2 基于IAE提取趋势项

2.1 h－步平滑法

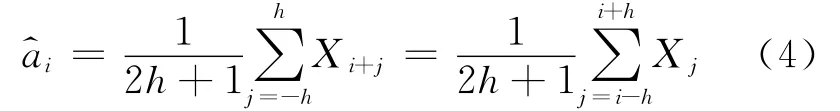
同理对Yi＋j≈bi＋εi＋j′，－h′≤j′≤h′，可得趋势项bi的估计.对应一组（h，h′），可得一组趋势项的估计，（h，h′）究竟取值多少才能使趋势项的估计最优，这个问题并没有解决.设h、h′满足已知，取最优的（h，h′）为此范围中使IAE达到最小者，此时得到的趋势项的估计达到最优.下面介绍本文所要研究的时间序列观测值，并用h－步平滑法提取趋势项.

例1h－步平滑法在股市上的应用

选取具有代表性的美国标准普尔500和NASDAQ周收盘价为研究对象，从2007－01－03～2008－12－08共计有102组数据中xi为标准普尔500周收盘价，yi为NASDAQ周收盘价.先利用h－步平滑法求出趋势项的众多估计值，然后在IAE衡量模型下找到一组使趋势项的估计最优的（h，h′），在（h，h′）＝（4，9）下算得趋势项的估计值并做图1[5、6].

2.2 指数加权平均法

h－步平滑估计用法简单，其局限性在于忽略超出观测时间范围的那些数据，这种不对称平均可能会产生边界偏倚.通过引进一个加权设计，可对滑动平均估计进行改善，具体改动如下：其中权数同理可得均是大于零的常数.通过IAE法则算出一个最优的权重λ1和λ2，使得积分绝对误差最小.

例2 指数加权平均法在股市上的应用

在IAE法则下寻找一个最优的权重λ1和λ2.图2是指数加权平均法给出的趋势项的估计值.

在图3中，虚线代表h－步平滑法提取趋势项后的残差波动，实线代表加权平均法提取趋势项后的残差波动.两者相比，加权平均法的残差波动近乎一条0均值的直线.注意，波动幅度越小不代表趋势项的估计效果越好，亦可能是时间序列中的波动项没有与趋势项分离，加权平均法提取的趋势项中必然含有方差较大的随机因素.

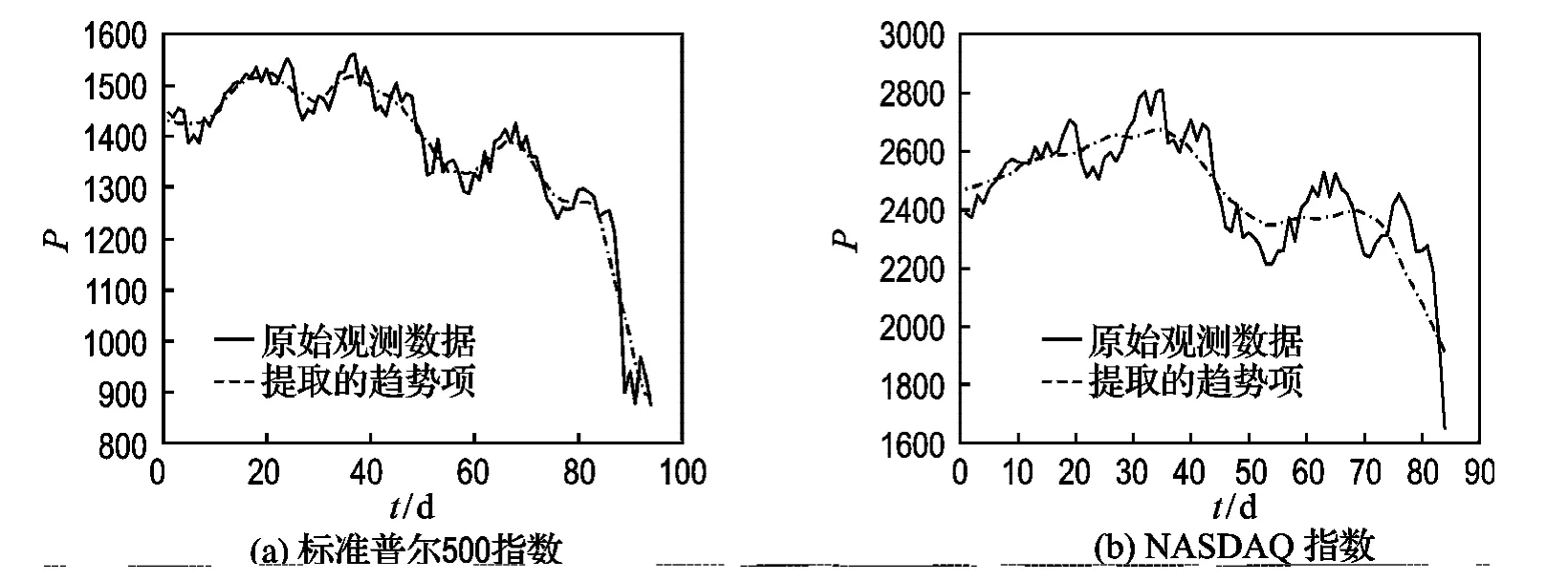
图1 h－步平滑法下针对两类指数提取趋势项Fig.1 Extracting trends of two indexes by h－step smoothing method

图2 在加权平均法下分别对两类指数提取趋势项Fig.2 Extracting trends of two indexes by weighted average method

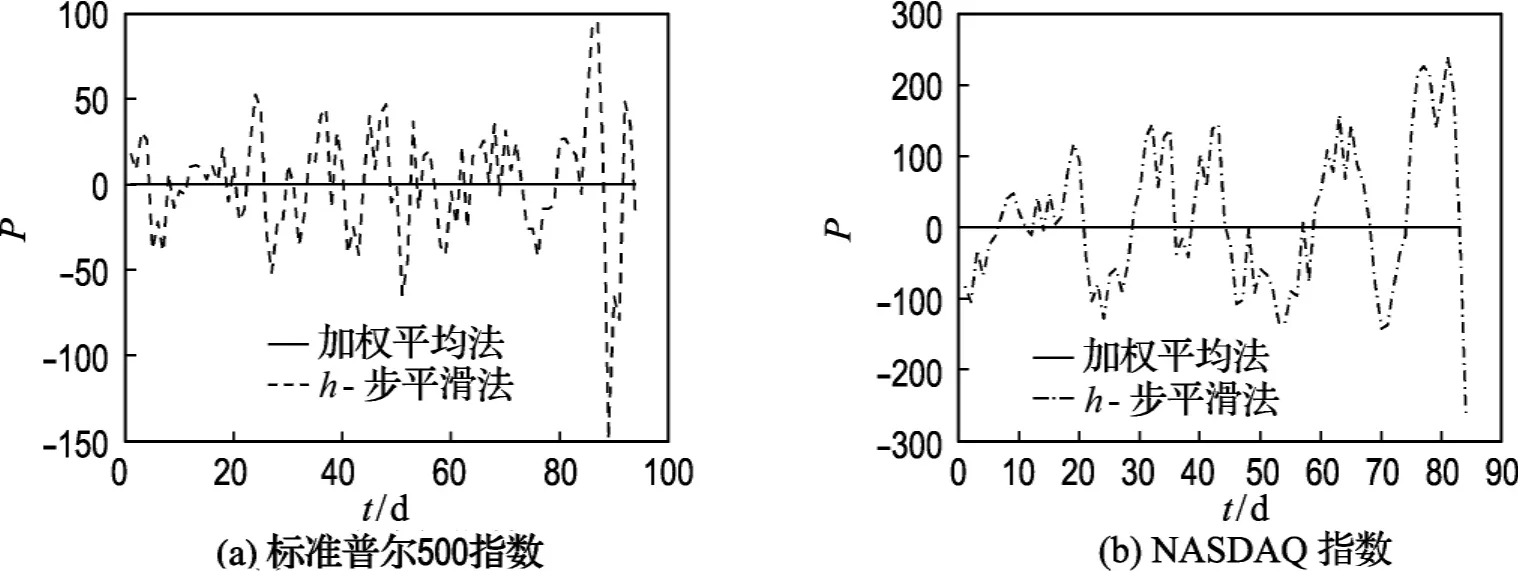
图3 h－步平滑法与加权平均法针对两类指数提取趋势项后的残差图像的比较Fig.3 Comparison on residual error of extracting trends between the h－step smothing method and weighted average method

3 建立趋势项序列的递推函数关系

针对次贷危机下的美国证券市场系统，先从线性的角度来寻找函数关系，并进行预测.

3.1 线性回归法

模型如下：

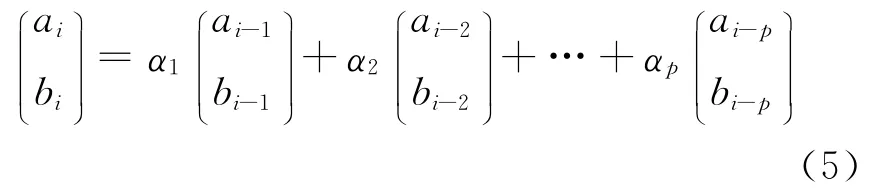
其中p是正整数，根据经验令p＝3，α1、α2和α3是

未知参数，有如下形式：

例3 线性回归法在股市上的应用

以例1中h－步平滑法估计出的趋势项估计为原始数据，用趋势项前半段数据得到了模型（5）的3个未知参数的估计和图4是由该线性模型模拟的证券市场走势的图像.

图4 线性回归法对两类指数提取趋势项Fig.4 Extracting trends of two indexes by linear regression method

易见此方法估计出来的市场走势明显与事实不符，由此初步断定美国证券市场系统是非线性的.

3.2 二次多项式法

其中c1，c2，…，c6未知.应用h－步平滑法求出趋势项的估计值c＾1，c＾2，…，c＾6，得二次多项式模型

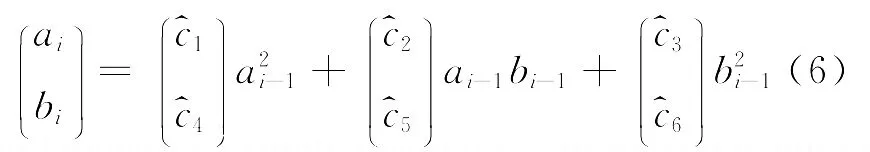
例4 二次多项式法在股市上的应用

由例1中h－步平滑法估计趋势项，得到趋势项的估计值.用h－步平滑法得到的趋势项估计值的前半段来估计二次多项式模型的6个未知参数.图5是二次多项式模型趋势项的估计值图.

易知线性回归法和二次多项式法对趋势项估计很差，下面用分段线性函数来给美国证券系统建模.

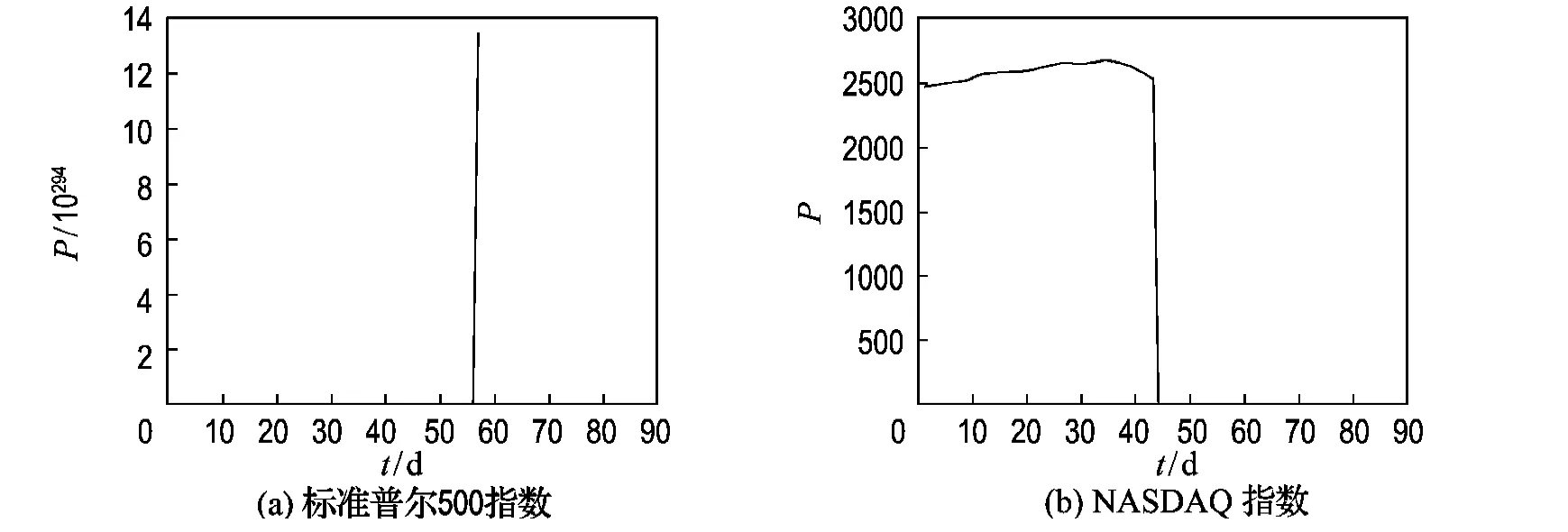
图5 二次多项式法对两类指数提取趋势项Fig.5 Extracting trends of two indexes by quadratic polynomials

3.3 分段线性方法

对于来自非线性系统的时间序列来说，分段线性函数简单易行，分段线性数学模型如下：

设α＝t0＜t1＜…＜tm＝β是区间[α，β]上的一种分割，记Ij（t）＝I（tj－1≤t＜tj）（1≤j＜m－1），Im（t）＝I（tm－1≤t＜tm），b＝（b0b1…bm）T，记

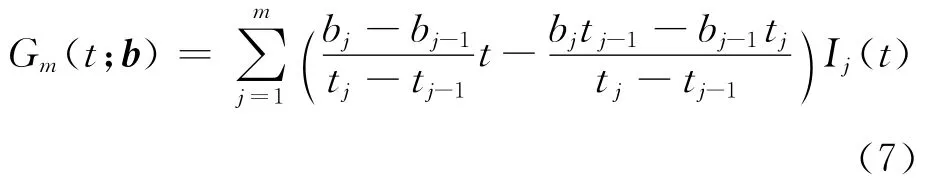
为依次连接点（t0，b0），（t1，b1），…，（tm，bm）的分段线性函数，称b为Gm的系数.

例5 分段线性法在股市上的应用

由例1中h－步平滑法估计趋势项，在本例中取m＝4，用h－步平滑法得到的趋势项估计值的前半段数值，来估计分段线性模型的5个未知参数，然后预测后半段并与实际进行比较，详见图6.

分段线性方法对趋势预测比线性回归法为好.不足之处：一是它没有反映市场走势的波动，二是真实市场是剧烈震荡向下发展，而预测却是在高位平缓.由此引入动力系统方法来研究美国股市，最终给出市场的走势预测.

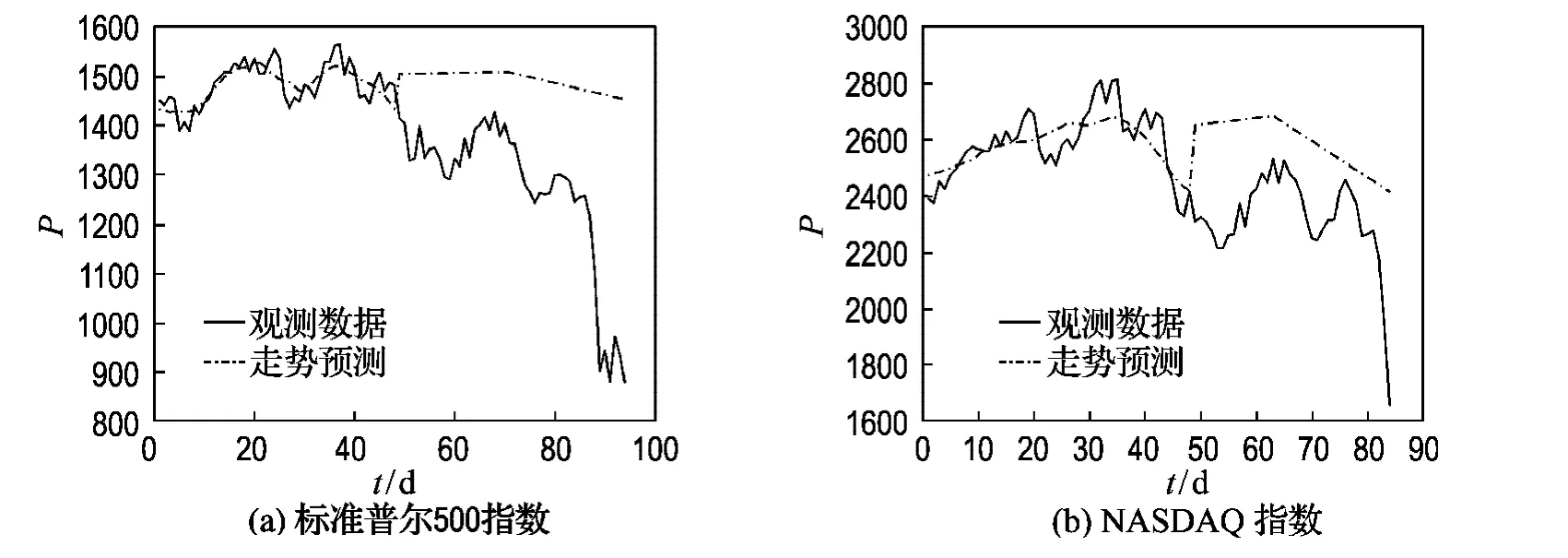
图6 分段线性方法对两类指数提取趋势项Fig.6 Extracting trends of two indexes by piecewise linear method

4 动力系统方法

对于未知数学模型的混沌动力系统，通过观测或实验手段可以获得多变量时间序列[7].Takens和Mane的延迟嵌入定理证明了只要适当选取延迟时间间隔τ和嵌入维数m，原未知数学模型的混沌动力系统的几何特征与重构的m维状态空间的几何特征是等价的，这意味着原来未知数学模型的混沌动力系统中的任何微分或拓扑不变量可以在重构的状态空间中计算，并且可以通过在重构的m维状态空间中建立数学模型对原未知数学模型的动力系统进行预测.

记观测到的多变量时间序列为｛xl，n｝Tn＝1（l＝1，2，…，L），假设T＝N＋P，前N个数据作为构造模型所需的样本，后P个数据作为预测精度的度量.采用延迟重构法，在相空间中重构的状态向量为

或者得到多元函数Gl：Rm→R，满足

例6 动力系统在股市上的应用

用标准普尔500和NASDAQ周收盘价作为时间序列观测样本.观测的范围从1988－01－04～2009－02－09，共1102组数据.将1988－01－04～2008－12－08共计1092组数据作为构造模型所需的样本，将最后10个数据作为预测精度的度量，用这10个数据与动力系统模型的预测结果进行比较.

首先确定延迟时间间隔τ，采用自相关函数法，可得到两类股市关于τ的图像，观察图像，得到标准普尔500指数的CL（τ）第一次取0值时的时间间隔τ1＝31，NASDAQ指数的τ2＝30.

其次确定相空间的维数m，由于观测数据是二维的，有m＝m1＋m2.于是用虚假邻点方法估计，得m1＝4和m2＝5[7].进一步，对于原始时间序列｛xl，n｝1092n＝1（l＝1，2），采用延迟重构法进行相空间重构.通过局部多项式预测法对未知系数进行估计，并对系统的走势进行了短期预测，为了便于分析截取了包含10个预测数值的后102个数据作图，最终得到图7.

图7 动力系统对两种指数短期预测Fig.7 Shortdated prediction on two indexes using dynamical method

图7中最后一小段10个数值是动力系统方法对该系统预测值.从图中直观上可以看出动力系统方法对NASDAQ指数市场走势预测得很好，但是对标准普尔500市场指数预测得不是很好.原因在于，NASDAQ指数的特点是收集和发布包含场外交易非上市股票的证券商报价的平均指数，股指中对股票的选择变动不大.而标准普尔500是由上市公司股票500只成分股组成的，并且该指数的成分股是变动的，对美国证券市场的指数选择不同对分析结果可能会有影响.从波动的同步性看，对最后10个数值预测的走势与真实数值的走势具有比较同步的波动，不论是震荡的幅度还是方向都与真实的走势相一致，只是数值上比真实数值普遍大400左右.数值上的差异可以用经济环境的异常来解释.最后10个数值所处的时间段是2008年12月至2009年2月初，这段时间内美国的经济徘徊在崩溃的边缘.银行机构继华尔投行后又掀起一轮破产潮，美国的实体经济以三大汽车生产商为代表流动性枯竭，政治上美国总统换届，经济刺激方案面临着极大的不确定性.面对如此恶劣的经济环境，标准普尔500指数的走势已经不再沿着历史正常波动，所以用20 a的历史数据来建立动力系统模型，是对处于正常状态的指数走势的预测，那么在异常状态下必然会与真实值有所差别.对于异常状态的美国股市，经济分析师都会下调股指走势的预期，预测值和真实值之间的差别可以很好地处理，用动力系统预测的指数震荡的幅度和方向还是比较准确的，因此可以作为经济决策的辅助数据.从这一点看来，动力系统方法在美国股市这个复杂系统上的预测还是很有意义的.