一种基于极端学习机的半监督学习方法

唐 晓 亮， 韩 敏

（大连理工大学 信息与通信工程学院，辽宁 大连 116024）

0 引 言

半监督学习方法是近年来提出的一类能够同时利用标记样本和无标记样本的机器学习方法[1～3]，其主要目标是通过发掘无标记样本的信息来弥补标记样本不足带来的影响.很多学者在不同领域提出了较为成功的半监督学习模型.例如，Bruzzone等[4]提出了直推式支持向量机（TSVM）用于遥感影像的半监督分类；Nigam等提出基于EM 算法的高斯混合模型（EM－GMMs）[5]，该模型通过 EM 算法的迭代计算实现了利用无标记样本和标记样本共同调节高斯混合模型参数的目的；Zhou等提出基于3个分类器的循环训练方法（tri－training）[6]，该方法弥补了协同训练（co－training）[7]对标记样本数量要求苛刻的不足，能够更好地提高分类器的半监督学习能力.当前半监督学习方法的研究中主要存在两个问题：（1）学习速度缓慢.例如，直推式支持向量机的学习过程实质上是一个NP问题[4]，需要消耗大量的运算时间；基于EM算法的半监督分类方法[5]迭代次数过多也会导致学习速度下降.学习速度缓慢造成半监督分类方法难以适应大数据量的分类要求.（2）不确定性递增.半监督学习方法主要通过扩充标记样本数量达到增加学习样本信息量的目的，但学习样本的不确定性也随着自身的扩充而逐步增加[8].例如，基于自训练的EM算法[3]对无标记样本进行临时标记，并将标记结果用于下次迭代训练，被错误标记的学习样本会引起学习过程中的误差传递，影响学习效果.

针对上述问题，本文提出一种基于极端学习机[9、10]的半监督学习方法.其基本思想是将极端学习机从监督学习模式扩展到半监督学习模式，再利用输出阈值向量控制标记样本的扩充程度，采用“换位”策略评估扩充样本中不确定性的影响.

1 极端学习机的学习模式

传统前馈神经网络多采用梯度下降算法调整权值参数，学习速度缓慢、泛化性能差等问题是制约前馈神经网络应用的瓶颈[11].最近 Huang等[9、10]摒弃了梯度下降算法的迭代调整策略，提出了极端学习机算法.该算法对单隐层神经网络的输入权值和隐层节点偏移量进行随机赋值，并且只通过一步计算即可解析求出网络的输出权值.极端学习机能够极大地提高网络学习速度和泛化能力.本章首先介绍极端学习机的监督学习模式，在此基础上推导出极端学习机的半监督学习模式.

1.1 极端学习机的监督学习

单隐层神经网络监督学习的代价函数E0可表示为

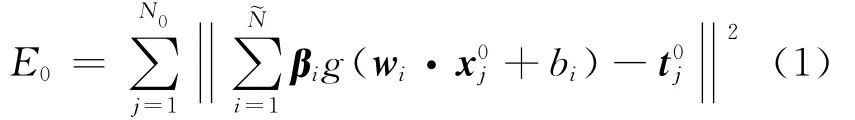
式中：N0为标记样本总数；为隐层节点总数，表示第j个标记样本向量（下标n表示每个样本向量的维数，n等于输入层节点数，表示样本向量的类别标记向量（下标C表示类别数目，C等于网络的输出节点数）；wi＝ （wi1…win），表示连接网络输入层节点与第i个隐层节点的输入权值向量；bi表示第i个隐层节点的偏移量；g（·）表示隐层节点的激活函数；βi＝ （βi1…βiC）T，表示连接第i个隐层节点与网络输出层节点的输出权值向量.

Huang等[9、10]指出最小化E0等价于找到满足下式的特殊解和

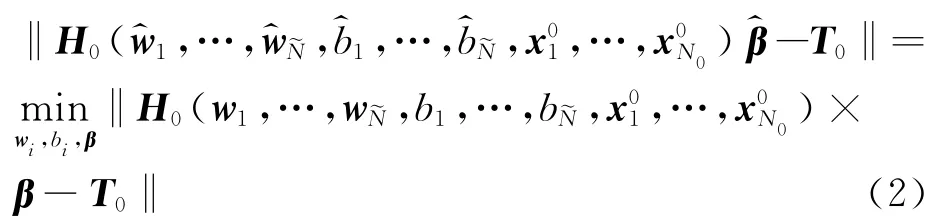
式中：H0表示网络关于标记样本的隐层输出矩阵；β表示输出权值矩阵；T0表示标记样本集的类别标记矩阵.H0、β、T0分别定义如下：

Huang等[9、10]严格地证明了当网络隐层节点的激活函数无穷可微时，网络的输入权值和偏移量可直接随机赋值而不必采用梯度下降算法迭代调整.因此单隐层神经网络的监督学习过程可等价为求取线性系统H0β＝T0的范数最小的最小二 乘 解 （minimum norm least－squares solution），如式（5）所示：

其中是矩阵H0的 Moore－Penrose广义逆[12]，在rank（H0）＝N珦的条件下可由正交投影方法求得.

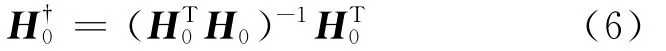
（1）对网络的输入权值向量wi和隐层节点偏移量bi进行随机赋值

（2）按照式（3）计算隐层输出矩阵H0；

1.2 极端学习机的半监督学习

关于极端学习机的已有研究均是在监督学习模式下进行的[9、10]，本节将极端学习机的学习模式扩展到半监督领域.首先考虑单隐层网络半监督学习的代价函数[9]：

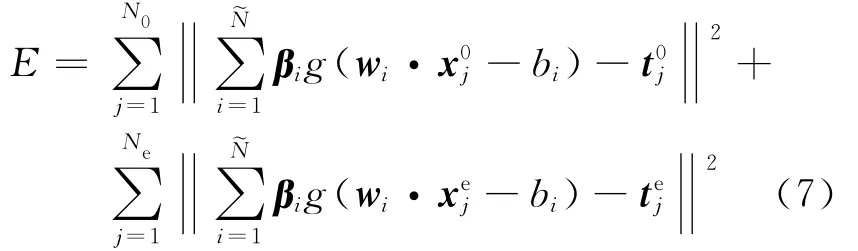
式（7）右边第2项为扩充的标记样本误差累加项；Ne表示扩充的标记样本的数目，表示第j个扩充的标记样本向量，表示的类别标记向量.

最小化半监督学习的代价函数等价于找到满足下式的特殊解：

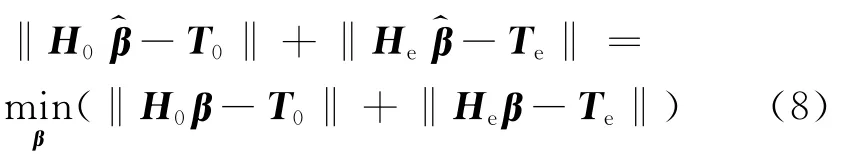
其中He表示网络关于扩充标记样本的隐层输出矩阵，Te表示扩充标记样本集的类别标记矩阵，分别定义如下：

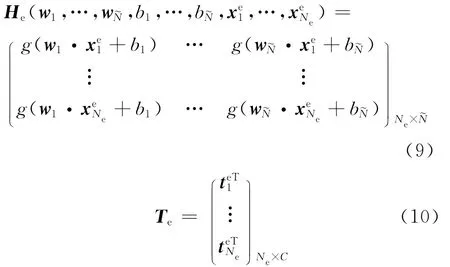
式（8）的右边可进一步推导如下：

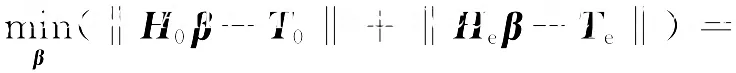
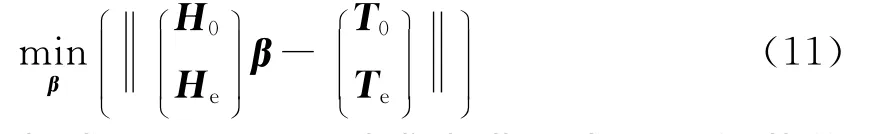
与式（5）同理，可以求出满足式（11）的范数最小的最小二乘解

与式（6）同理，可以进一步推出的具体形式：

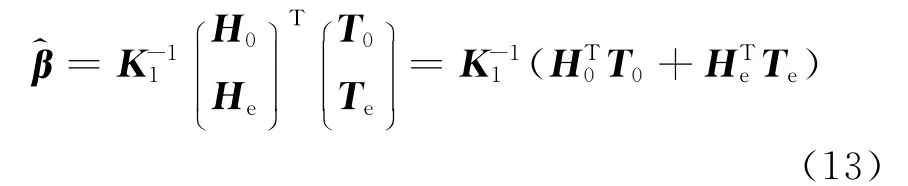
其中

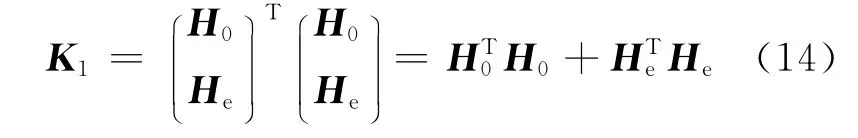
除了计算输出权值矩阵，极端学习机的半监督学习过程还涉及如何扩充标记样本以及评估不确定性等操作，第2章将对所有相关步骤进行详细描述.

2 基于极端学习机的半监督学习方法流程

基于极端学习机的半监督学习方法主要包括4个步骤：初始训练、标记样本扩充、不确定性的换位评估和输出权值计算.

2.1 方法流程归纳

初始输入：初始标记样本集L0，无标记样本集U，单隐层神经网络的隐层节点数.

步骤1 初始训练

（1）对网络的输入权值矩阵W＝（wi）和隐层节点偏移向量B＝ （bi）进行随机赋值，i＝1，2，…，；

（2）按照式（3）计算关于初始标记样本集L0的网络隐层输出矩阵H（W，B，L0）；

（3）按照式（5）和（6）计算网络的隐层输出权值矩阵；

（4）计算输出阈值向量Θ：

①计算网络输出层的初始输出矩阵

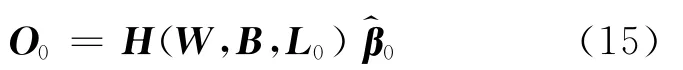
其中O0表示网络关于集合L0的输出层输出矩阵，具体形式为N0表示集合L0的样本总数.

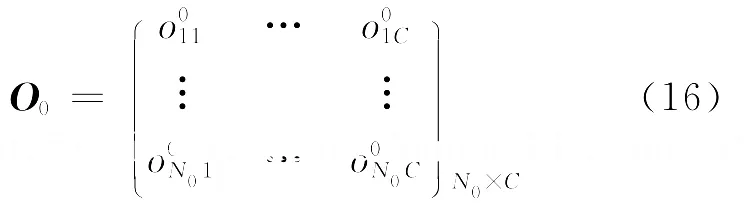
②计算网络的输出阈值向量

其中θk表示关于类别k的网络输出阈值，θk＝为初始标记样本集L0中属于类别k的样本数目；表示O0中第j行第k列元素值；Δ∈（0，1），表示输出裕量参数；分段函数定义如下：

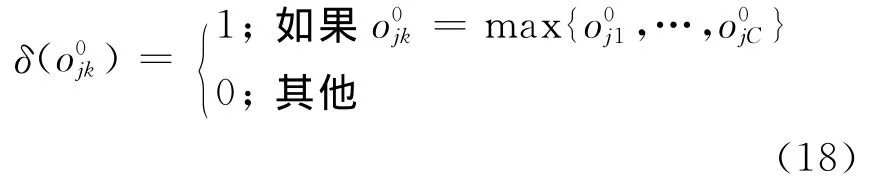
（5）存储输入权值矩阵W＝ （wi）、偏移向量B＝ （bi）和初始输出权值矩阵

步骤2 标记样本扩充

（1）计算关于无标记样本集U的输出层输出矩阵：

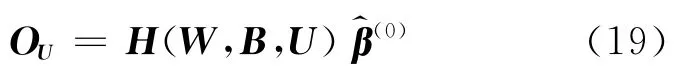
其中H（W，B，U）表示网络关于无标记样本集U的隐层输出矩阵，OU表示网络关于无标记样本集U的输出层的输出矩阵，具体定义如下：H（W，B，U）＝

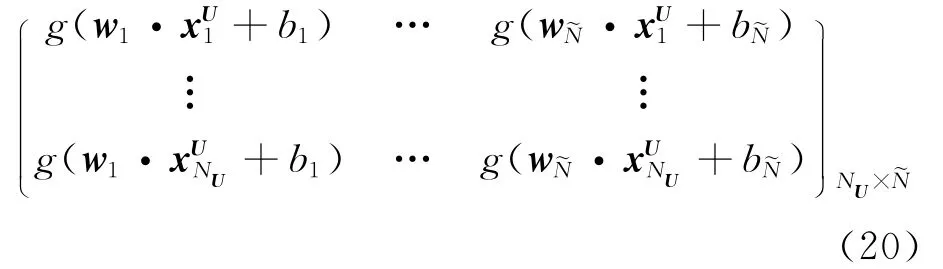
xU1，…，xUNU为集合U中的无标记样本向量，下标NU表示集合U中无标记样本向量的总数.

（2）构建扩充标记样本集合Le

步骤3 不确定性的换位评估

因为无法直接评估扩充样本中的不确定性对分类结果的影响，所以采用标记样本集与扩充标记样本集交换位置的策略间接评估不确定性的影响.

（1）仅以扩充标记样本集Le为学习样本集，计算对应的输出权值矩阵：

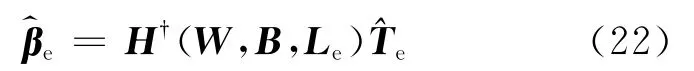
其中为利用Le训练的网络输出权值矩阵，表示Le的类别标记矩阵，H（W，B，Le）是网络隐层输出矩阵H（W，B，Le）的 Moore－Penrose广义逆，H（W，B，Le）的计算过程可参照式（6）.

（2）以初始标记样本集L0为测试对象，检验扩充标记样本集的不确定性：

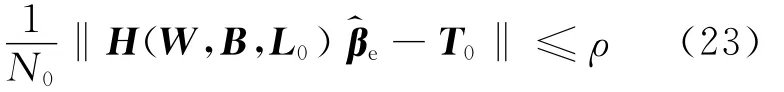
其中ρ＞0，表示不确定性阈值.

如果能够满足式（23），证明扩充样本的不确定性不足以影响分类结果，转到步骤4；否则，将Le中的样本清除，并增大输出阈值Θ，

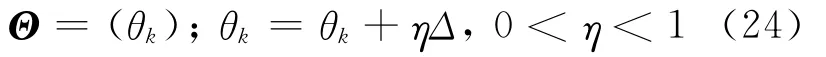
转到步骤2重新扩充标记样本.

步骤4 输出权值计算

（1）针对样本集合L0和Le，以W为输入权值矩阵、B为偏移向量，计算网络的输出权值矩阵

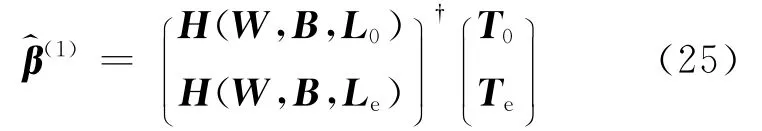
具体计算过程可参照式（12）～（14）.

（2）判断

极端学习机的分类过程如下：

（1）根据学习结果（W，B，），计算网络关于测试样本集合Ω的输出层输出矩阵OΩ：

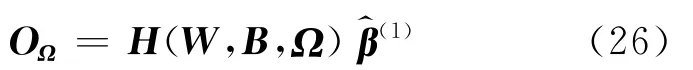
其中

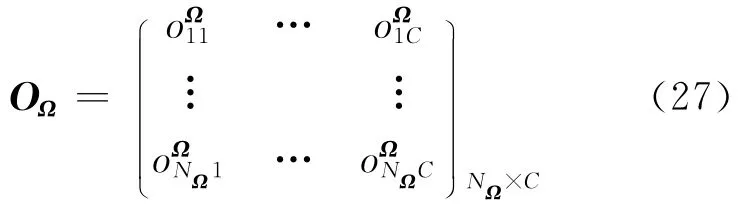
NΩ为测试样本的数目，C为类别数目.

2.2 关键参数的作用和选择策略

在半监督学习过程中，式（17）的输出裕量参数Δ和式（23）的不确定性阈值ρ对算法的成绩影响较大.其中Δ影响无标记样本向标记样本转化的难易程度，Δ越大无标记样本越容易转化为标记样本，反之越难；ρ控制换位评估过程中的分类误差上限，ρ越小表示算法允许的误差上限越低，算法对不确定性的敏感性就越高，算法的重复次数也越多.

Δ与ρ的取值范围均为（0，1），仿真实验采用基于交叉检验（cross validation）[13]的网格搜索法对这两个参数进行选择，交叉检验方法可以保证参数的无偏估计.具体过程如下：（1）Δ与ρ取离散值（例如，Δ＝ …，10－4，10－3，…，10－1，…；ρ＝ …，10－4，10－3，…，10－1，…）构成网格；（2）计算在网格对应的每个参数对（如（Δ，ρ）＝ （10－1，10－1））处的交叉检验值在最大交叉检验值对应的参数对附近区域进行更为精细的网格搜索.例如，初始得到的最优参数对为（Δ，ρ）＝ （10－1，10－1），则在（10－1，10－1）周围进行精细网格搜索（Δ＝ …，0.8×10－1，0.9×10－1，10－1，1.1×10－1，1.2×10－1，…；ρ＝ …，0.8×10－1，0.9×10－1，10－1，1.1×10－1，1.2×10－1，…），直至确定最优参数值.

3 仿真实验

为验证本文所提方法的有效性，对扎龙自然保护区遥感数据集[14]、UCI机器学习数据库[15]中的3组数据集以及2组半监督学习基准数据集[1]进行分类仿真.每组样本的个数、类别数等相关信息如表1所示.为了全面检验半监督学习方法的学习速度和泛化能力，将每组训练样本中的标记样本和无标记样本的比例按1∶1、1∶2和1∶3进行分配，分别求取半监督学习方法在不同分配比例条件下的学习时间和分类精度.

采用改进型 TSVM 方法（NTSVM）[4]、EMGMMs方法[5]和本文提出的基于极端学习机的半监督学习方法（下文简称ssELM）对实验数据进行分类.所有程序均在Matlab 7平台上运行，计算机CPU为Pentium IV 2.0 GHz，内存512 MB.3种方法的半监督学习时间和分类精度分别如表2和3所示.

通过仿真结果可以看出，NTSVM方法虽然能够取得较高的分类精度，但仍需消耗大量的学习时间，而且随着无标记样本比例的上升学习时间明显增加.EM－GMMs方法对标记样本的依赖程度较高，其分类精度随标记样本比例的减小而大幅度下降.与其他两种半监督学习方法相比，本文所提方法能够显著提高半监督学习的速度；同时受无标记样本比例变化的影响较小，在无标记样本比例增大的情况下仍能取得较高的分类精度.

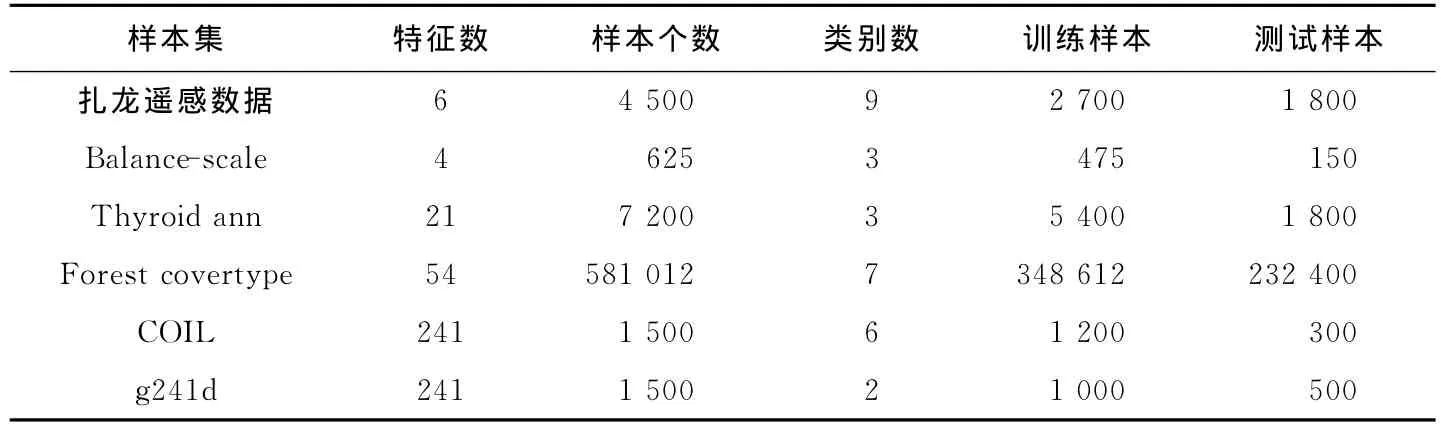
表1 实验样本相关信息Tab.1 Information of experimental samples

表2 三种方法对6组实验数据的半监督学习时间Tab.2 Semi－supervised learning time of three methods for six experimental data sets s

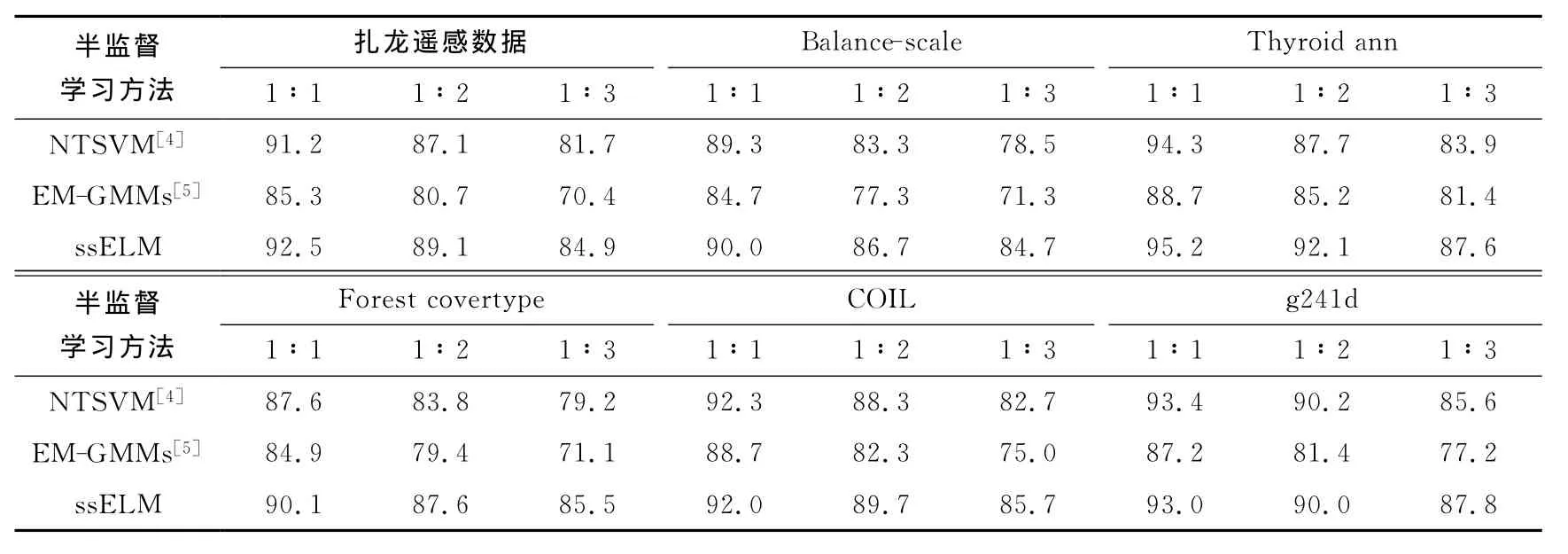
表3 三种方法对6组实验数据的分类精度Tab.3 Classification accuracies of three methods for six experimental data sets %

如表3所示，在标记样本与无标记样本比例为1∶1和1∶2时，ssELM方法对数据集g241d的分类精度比NTSVM方法稍低.这是因为初始标记样本集中包含的异常点较多，导致ssELM方法对不确定性检测的精度有所下降.减少标记样本集中的异常点影响是半监督学习方法性能稳定的关键.实验结果证明本文所提方法能够有效地发掘无标记样本中的有用信息，并在一定程度上抑制样本扩充带来的不确定性增加等问题.

4 结 论

学习速度缓慢、不确定性递增是半监督学习方法存在的两大问题，针对这些问题本文提出一种基于极端学习机的半监督学习方法.该方法主要包括初始训练、标记样本扩充、不确定性的换位评估和输出权值计算4个步骤.该方法将极端学习机从监督学习模式扩展到半监督学习模式，极大地提高了半监督学习的速度.在半监督学习过程中，该方法利用输出阈值向量控制标记样本的扩充程度，以标记样本和扩充样本之间的换位策略评估不确定性对学习效果的影响.仿真结果证明了本文所提方法在提高半监督学习速度、抑制不确定性增加以及提高分类精度等方面的有效性.

[1]CHAPELLE O， SCHLKOPF B， ZIEN A.Semi－supervised Learning [M]. Cambridge：MIT Press，2006

[2]孙广玲，降 龙.基于分层高斯混合模型的半监督学习算 法 [J].计 算 机 研 究 与 发 展，2004，41（1）：156－161

[3]张博锋，白 冰，苏金树.基于自训练EM算法的半监督文本分类[J].国防科技大学学报，2007，29（6）：65－69

[4]BRUZZONE L，CHI M M，MARCONCINI M.A novel transductive SVM for semisupervised classification of remote－sensing images [J].IEEE Transactions on Geoscience and Remote Sensing，2006，44（11）：3363－3373

[5]NIGAM K，MCCALLUM A K，THRUN S，etal.Text classification from labeled and unlabeled documents using EM [J].Machine Learning，2000，39（2－3）：103－134

[6]ZHOU Z H，LI M.Tri－training：Exploiting unlabeled data using three classifiers[J].IEEE Transactions on Knowledge and Data Engineering，2005，17（11）：1529－1541

[7]WANG W，ZHOU Z H.Analyzing co－training style algorithms[C]//Proceedings of the 18th European Conference on Machine Learning （ECML′07）.Poland：Springer－Verlag，2007：454－465

[8]COHEN I， COZMAN F G，SEBE N，etal.Semisupervised learning of classifiers：theory，algorithms，and their application to human－computer interaction [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26（12）：1553－1566

[9]HUANG G B，ZHU Q Y，SIEW C K.Extreme learning machine：Theory and applications [J].Neurocomputing，2006，70（1－3）：489－501

[10]HUANG G B，ZHU Q Y，MAO K Z，etal.Can threshold networks be trained directly？[J].IEEE Transactions on Circuits and Systems II－Express Briefs，2006，53（3）：187－191

[11]李鸿儒，顾树生.一种递归神经网络的快速并行算法[J].自动化学报，2004，30（4）：516－522

[12]SERRE D.Matrices：Theory and Applications[M].New York：Springer－Verlag，2002：145－147

[13]SUNDARARAJAN S，SHEVADE S，KEERTHI S S.Fast generalized cross－validation algorithm for sparse model learning [J].Neural Computation，2007，19（1）：283－301

[14]韩 敏，程 磊，唐晓亮.Fuzzy ARTMAP神经网络在土地覆盖分类中的应用研究 [J].中国图象图形学报，2005，10（4）：415－419

[15]ASUNCION A，NEWMAN D J.UCI machine learning repository[DB/OL].[2008－03－26].http：//www.ics.uci.edu/ ～ mlearn/ MLRepository.html