钢管混凝土哑铃形梁有限元分析

(福建农林大学交通学院，福建 福州 350002)

钢管混凝土结构在桥梁上的应用同时解决了拱桥高强度材料应用和施工2大难题，因此，钢管混凝土拱桥在我国得到迅速的发展[1]。钢管混凝土拱桥的主拱圈截面形式主要有单圆管、哑铃形和桁式3种，其中哑铃形是最主要的截面形式。单圆管截面由于截面抗弯惯性矩比较小，抗弯效率太低，一般应用在小跨径的桥梁中。桁式截面由于节点构造复杂、疲劳问题比较突出。哑铃形截面由上下两圆管加腹腔组成，其中上下两圆管受力和单圆管截面类似，腹腔内受力比较复杂。传统的哑铃形截面由于腹腔内灌注混凝土时易发生爆管事故[2]，文献[3]中提出了腹腔内不灌混凝土而以H型钢加劲的新型哑铃形截面，但未对这2种哑铃形截面展开试验研究和有限元研究。笔者曾进行了4根哑铃形钢管混凝土梁的试验，研究了腹腔内灌注混凝土的传统哑铃形截面梁和腹腔内不灌混凝土而以H型钢加劲的新型哑铃形截面梁的受力性能[4]。下面，笔者应用Fortran语言编制了有限元程序US-CFSTA，对这2种截面形式的钢管混凝土哑铃形梁进行了有限元分析。

1 试件断面形式

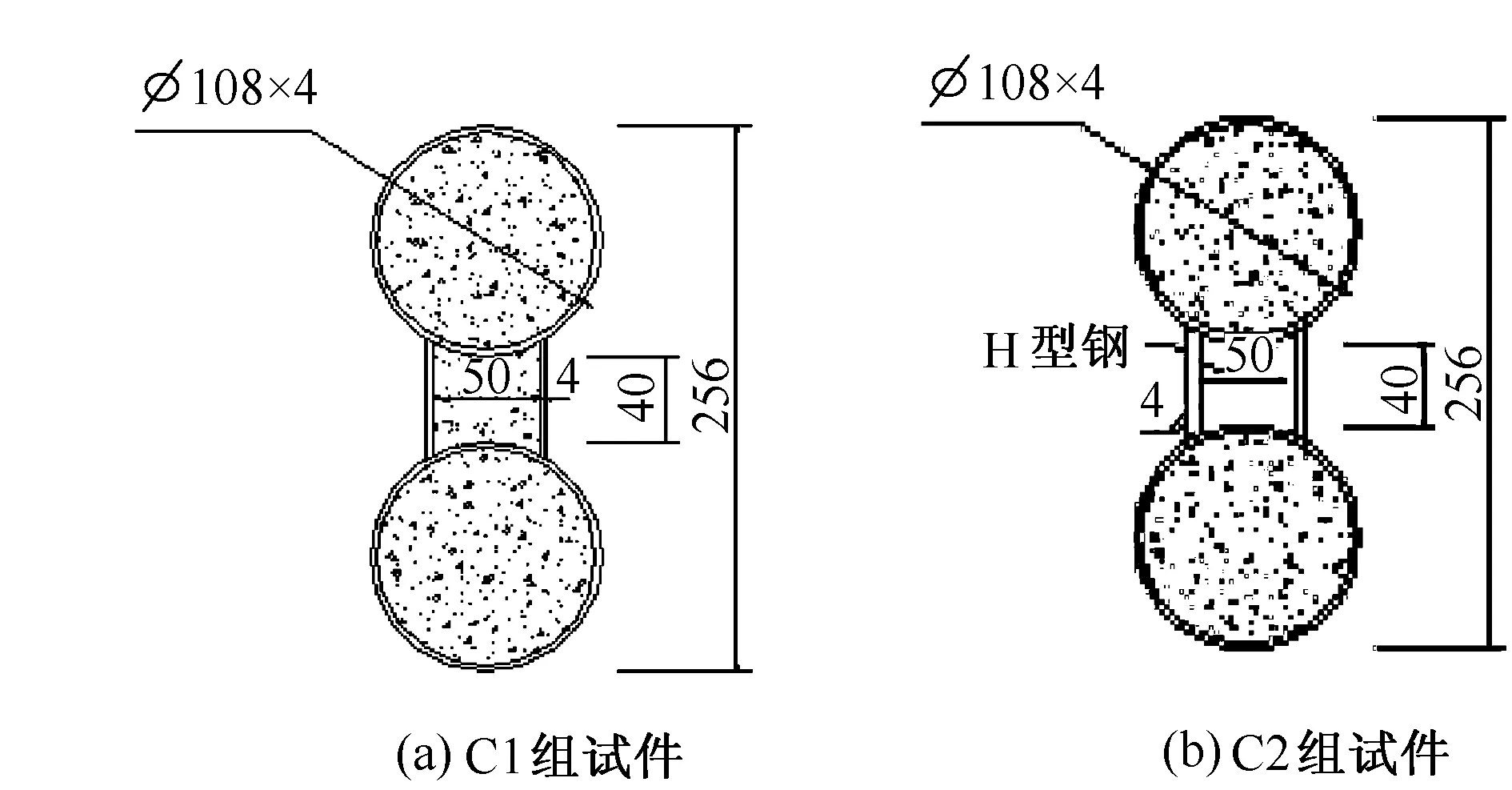
图1 试件截面(单位：mm)

试件长度为2000mm(净跨为1880mm)，试件的截面尺寸由2根∅108mm×4mm的无缝钢管和4mm厚、相距50mm的腹板焊接而成。试件分为C1、C2两组，2组试件的上下钢管混凝土及钢腹板的尺寸与材料均相同，不同的是腹腔内C1组填有混凝土，C2组不填混凝土、2腹板之间用H型钢横向加劲。H型钢由厚4mm的钢板焊成，沿长度方向80mm 1个。试件截面见图1。每组试件均有2个，笔者提供的每组试件的数据均取组内试件的平均值。

2 有限元计算方法

以这4根试验构件作为研究对象，采用自编的有限元程序US-CFSTA对其进行有限元分析，并将有限元计算结果与试验结果对比，验证有限元计算方法的正确性。

运用自编的有限元程序US-CFSTA进行有限元计算时，采用了如下基本假设：①加载过程中截面始终保持平面；②忽略剪应力和剪应变的影响；③钢管和混凝土之间无滑移现象；④某级荷载作用下单个条带内的应变是相同的；⑤单元两端之间的截面内力近似地按线性变化，取单元的平均刚度作为单元刚度。

当应力超出材料的弹性极限后，钢管和混凝土的弹性模量Es、Ec将随着应力大小而变化，截面应力-应变是非线性关系。结构的材料进入弹塑性阶段后，截面的抗压刚度EA及抗弯刚度EI在荷载增量不大、单元划分足够小时，可用条带中点的模量作为条带的平均模量，有下列物理关系：

Ni=ηiEAεi=AiεiMi=-ξiEIφi=-Biφi

(1)

图2 条带划分及应变分布图

式中，ξi、ηi为截面的抗弯、抗压刚度折减系数；Ai，Bi为抗压刚度及折减抗弯；φi，εi分别为截面曲率和截面几何中心的应变；Mi，Ni分别为截面弯矩和轴力。

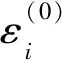
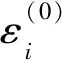
然后由材料的应力-应变关系求得分块的钢管和混凝土的应力σsi、σci，最后根据内外力平衡条件式(1)和下式：

(2)

有限元程序US-CFSTA中非线性解法采用混合法，混合法具有增量法和迭代法的优点，将荷载分成若干增量，给定参数，由程序控制加载步长，在各个增量荷载上进行迭代。

采用材料非线性和几何非线性相互嵌套的方法来求解双重非线性问题，即用增量法考虑材料的非线性影响，将几何非线性嵌入材料非线性的增量法之中，在每级荷载增量中，折减刚度不变，并用修正的Newton-Raphson方法考虑几何非线性问题。其求解步骤如下(变量之间的具体推导过程详见文献[5])：

1)在某级荷载作用下，调用哑铃形截面刚度计算的子程序迭代得第i个条带的抗压刚度和抗弯刚度EAi、EIi；

2)把EAi、EIi代入线性刚度阵[Ke]：

求出第一次迭代后的位移：

{δ}e={F}e{Ke}-1({F}e为各单元节点的杆端力)

及单元内力Ni，Mi；

4)求出杆件单元几何刚度矩阵[Kσ]：

从而定出切线刚度矩阵[KT]=[Ke]+[Kσ]；

6)求节点不平衡力{ΔP}，并求该力所引起的位移{Δδ}={ΔP}[KT]-1；

7)判断{Δδ}是否达到精度要求，如达不到要求则修正节点位移重复步骤4)～6)，直至达到要求；

8)变化节点坐标，判断是否荷载增量与结构最大的位移增量的比值小于给定的数值，如达不到再增加一级荷载，重复步骤1)～7)，继续计算直至达到要求，输出计算结果。

3 有限元模型中材料本构关系的选取

笔者在采用自编有限元程序US-CFSTA对哑铃形钢管混凝土结构进行有限元分析计算时，由于哑铃形梁中的上下圆钢管内的混凝土与单圆钢管混凝土的受力基本相同，因此，进行数值计算时采用单圆管钢管混凝土的本构关系，其中，钢管材料采用4段直线组成的应力-应变关系曲线：

弹性段：

σ=Esε(0≤ε≤εe1)

(3)

塑性段：

σ=fy(εe1<ε≤εe2)

(4)

强化段：

σ=fy+Es/150(ε-εe2) (εe2<ε≤εe3)

(5)

二次塑流段：

σ=fu(ε≥εe3)

(6)

式中，Es为钢材弹性阶段的弹性模量；εe1为弹性极限应变；fy和fu分别为钢材的屈服强度和极限强度。取屈服极限应变εe2=10εe1，强化极限应变εe3=100εe1，钢材极限强度fu=1.6fy。

混凝土采用文献[6]考虑套箍作用的本构关系模型-纤维单元模型。对于圆钢管混凝土：

上升段：

(7)

强化段(ε>ε0)：

(8)

而腹腔内混凝土与普通混凝土受力基本相同，可采用普通混凝土的本构关系，即美国学者Hognested在文献[7]中建议的曲线(由曲线段和下降段组成)：

上升段：

(9)

下降段：

(10)

式中，εu=0.035是极限应变；ε0=0.002是最大应力对应的应变;fc是混凝土的极限抗压强度。

混凝土单轴受拉的应力-应变关系采用文献[8]中提出的本构关系，为方便计算，笔者没有考虑受拉混凝土中的下降段，受拉区应力-应变关系模型简化为：

(11)

式中，峰值拉应力σp=0.26×(1.25fc)2/3；峰值拉应变εp=43.1σp(με)。

4 结果分析

图3分别为2组哑铃形梁(C1组和C2组)的荷载-中截面水平挠度的试验曲线和笔者提出的有限元自编程序US-CFSTA的计算曲线。由图3可见，有限元程序US-CFSTA能够比较准确地模拟哑铃形梁的受力全过程曲线，而通用有限元软件ANSYS，由于不能输入受拉混凝土的本构关系，无法模拟下圆管混凝土的受拉开裂状态，其计算结果与试验结果相比偏小。

图3 荷载-中截面水平挠度曲线

图4 极限承载力有限元计算值与试验值比较

C1组试件与C2 组试件比较，由于传统哑铃形截面腹腔内混凝土对抗弯承载力的贡献不大，其试验结果和计算结果与腹腔内不灌混凝土而以H型钢加劲的新型哑铃形截面梁相差不大。这说明应用新型哑铃形梁，并不会导致抗弯承载力的减弱。

图4给出了抗弯极限承载力试验值及有限元计算值的比较。从图4可以看出，采用自编的有限元程序US-CFSTA的计算值与试验结果十分接近，误差在10%以内，说明该有限元计算方法可用于哑铃形钢管混凝土梁极限承载力的计算。

5 结 语

由于钢管混凝土抗弯极限承载力计算是相当复杂的课题，目前对钢管混凝土的试验研究和理论探讨都非常少。笔者自编了有限元程序US-CFSTA，对钢管混凝土哑铃形梁进行了有限元分析。此有限元计算方法可以定义拉区混凝土的本构关系，并考虑拉区混凝土开裂退出工作面，与通用有限元软件ANSYS的计算结果相比，与试验结果吻合更好，可用于工程计算。

[1]陈宝春，杨亚林.钢管混凝土拱桥调查与分析[J].世界桥梁，2006，(2)：73～77.

[2] 秦荣，谢肖礼，彭文立，等.钢管混凝土拱桥钢管开裂事故分析[J].土木工程学报，2001，(3):74～77.

[3] 陈宝春，肖泽荣.钢管混凝土哑铃形拱肋灌注管内混凝土时的截面应力分析[J].中国公路学报，2005，18(1)：73～76.

[4] 盛叶,陈宝春.钢管混凝土哑铃形梁试验[J].哈尔滨工业大学学报，2003，35(z1)：248～251.

[5] 赵振铭，陈宝春.杆系与箱型梁桥结构分析及程序设计[D].华南理工大学出版社，1997.

[6] 陈宝春,秦泽豹,彦坂熙,等.钢管混凝土拱(单圆管)面内受力双重非线性有限元分析[J].铁道学报,2003，25(4):80～84.

[7] Hognested E.Hanson N W.Concrete stress distribution in ultimate strength design[J].ACI Journal,December,proceedings,1955，52(4):455～479.

[8] 沈聚敏，王传志，江见鲸.钢筋混凝土有限元与板壳极限分析[M].北京：清华大学出版社，1993.