调和方程Dirichlet外问题的Green函数研究
2010-05-29
(长江大学信息与数学学院,湖北 荆州 434023)
调和方程作为偏微分方程中最典型的一种,在研究调和场理论与电磁场的性质时常会遇到,而Green函数是求解调和方程边值问题的重要方法之一,在船舶磁场的计算[1]与物理大地测量学[2]等方面都有应用,因此对调和方程Green函数的研究既有理论意义又有实用价值。传统教材定义调和方程的Green函数有2种方式,分别是基本解方式[3]和狄拉克δ函数方式[4],文献[5]还讨论了2种定义方式的等价性,而且几乎以Dirichlet内问题进行讨论,只有文献[2]讨论了外问题的Green函数,但没有给出满足的条件。为此,笔者在以基本解方式定义Green函数的基础上,导出了有界区域外部调和函数的积分表达式,并在此基础上给出了Dirichlet外问题的Green函数及其满足的条件,最后用此Green函数给出了调和方程球域外Dirichlet问题的解❶。
1 有界区域外部调和函数的积分表达式

(1)

以M0为球心、充分小的正数ε为半径作球面Γε,记小球面所包围的区域为Kε⊂Ω′。再以原点O为球心、以任意大的正数R为半径作球面ΓR,使得ΓR包含Γ和Γε,并记ΓR与Γ所夹的区域为ΩR。在以Γ∪Γε∪ΓR为边界的区域ΩRKε上,对调和函数u,v应用格林第二公式[3]可得:
即:
(2)

从而:
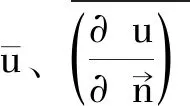
在大球面ΓR上,由文献[6]知:


由三角不等式rOM≤rOM0+rM0M可得:
在式(2)中,令ε→0,R→+∞可得:
(3)
式中,ΓR的法向量指向内侧。
2 Dirichlet外问题的Green函数及其满足的条件
作以原点O为球心,任意大的正数R为半径的球面ΓR,使得ΓR包含Γ,并记ΓR与Γ所夹的区域为ΩR。在以Γ∪ΓR为边界的区域ΩR上,对调和函数u、g应用格林第二公式[3]可得:
即:
(4)
在球面ΓR上,由于:
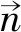
在式(4)中,令R→+∞可得:
(5)
式中,Γ的法向量指向内侧。
式(3)减去式(5)可得:
记:
并注意到u、g满足的边界条件,得到:
(6)
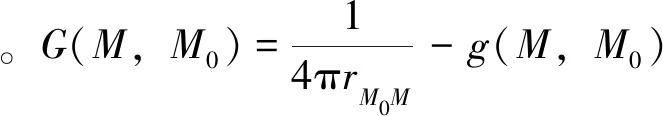
(7)
3 应 用
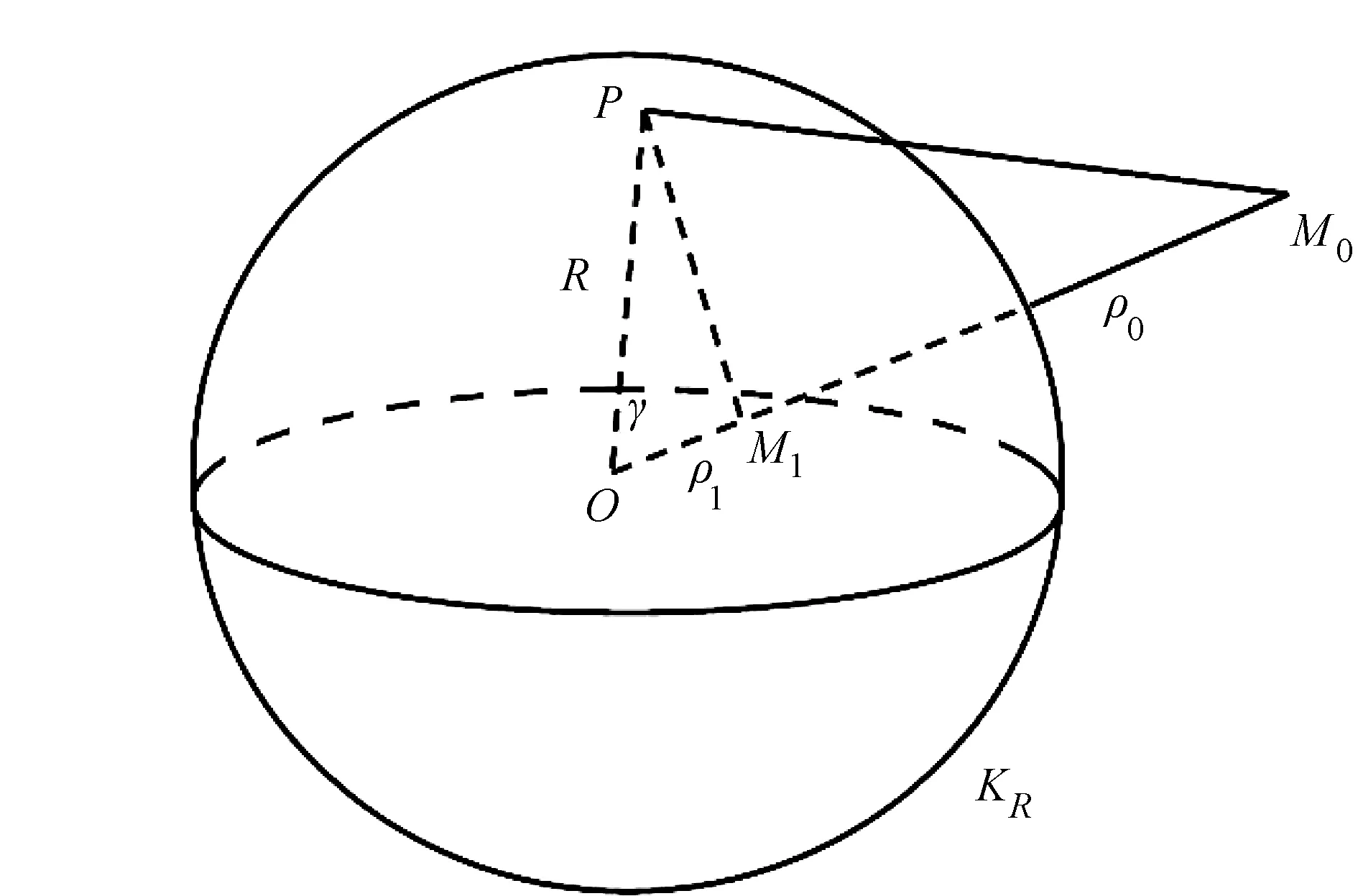
图1 静电源像法求Green函数示意图
作为Dirichlet外问题Green函数的应用,下面求解以原点O为球心,R为半径的球面KR外的Dirichlet外问题:
(8)
其中,u在KR上有一阶连续偏导数。
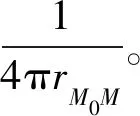
这是感应电荷的等效电位,其中q待定。
M处的总电位为:

由余弦定理及关系式ρ0ρ1=R2可得:
其中,γ是ρ0与ρ之间的夹角。显然g(M,M0)满足条件(7)。
由式(6)化为球坐标形式可得问题(8)的解为:
其中,cosγ=cosθcosθ0+sinθsinθ0cos(φ-φ0)。
[1]周耀忠.格林函数在船舶磁场计算中的应用[J].中国修船,2006,19(5):29~31.
[2]张传定,陆仲连.球域调和函数外部边值问题的格林函数解[J].解放军测绘学院学报,1994,11(3):161~165.
[3]谷超豪.数学物理方程[M].第2版.北京:高等教育出版社,2002.68~95.
[4]于涛.数学物理方程与特殊函数[M].哈尔滨:哈尔滨工程大学出版社,2006.99~116.
[5]柯导明,陈军宁.数学物理方法[M].北京:机械工业出版社,2008.297~311.
[6]赵天玉,刘庆.反演变换在调和函数研究中的应用[J].长江大学学报(自然科学版),2009,6(3):N1~4.
