空间自适应的快速粒子Level Set方法

黄筱云，李绍武

(天津大学建筑工程学院，天津 300072)

空间自适应的快速粒子Level Set方法

黄筱云，李绍武

(天津大学建筑工程学院，天津 300072)

Level set作为一种有效的界面追踪方法，已经被广泛地应用到单相流的自由表面追踪或多相流的交界面追踪.快速粒子level set方法(FPLS)是一种改进的level set方法，既具有较高的界面追踪精度，又有较高的计算效率.将其与自适应网格结合起来，提出了一种基于树型结构空间自适应的快速粒子 level set方法(SA-FPLS).通过在交界面附近设置高分辨率网格带，且只在高分辨率网格带内求解level set方程，既进一步提高了交界面模拟精度，又可以节省计算机内存，同时保持较高计算效率.

快速粒子level set；自适应网格；空间自适应的快速粒子level set

在用数值方法求解带有交界面的流体力学问题时，必须通过一定方法预先给出流体交界面的位置.level set方法是近年发展起来的一种界面追踪方法[1]，其原理是将交界面看作满足以下控制方程的符号距离函数φ的零等值线(面).

式中：φ称为level set函数，其值在交界面上为零，离开交界面为正或为负；ui为速度张量.

为使交界面的解在出现界面融合或较大φ值梯度时仍有较高的精度，一般采用重新初始化的方法[2]，即在每完成一步level set方程求解过程后，通过迭代求解方程

的解，来对level set函数进行初始化，其中0φ为level set方程的计算结果，xΔ为网格尺寸.这种level set方法在整个计算域上进行计算，称之为全局 level set方法.

为了减少计算量，Peng等[3]提出了一种局部的level set方法，它只需在交界面附近区域求解level set方程和重新初始化.事实上，level set方法中采用迭代法进行重新初始化是影响计算速度的关键因素，Sethian[4]提出了一种fast marching技术求解level set方程，其特点是无需重新初始化，但计算精度较低.

与VOF方法相比较，level set方法的缺点是守恒性差.为了弥补这一缺陷，Sussman等[5]将 VOF与level set方法相结合，提出了混合型的界面追踪方法——CLSVOF，该方法利用 VOF函数来校正 level set函数结果以达到减少质量损失的目的，但该方法并不能完全消除交界面附近的噪声，追踪到的交界面与实际值存在相位差.另外一种改进的level set方法是粒子level set(PLS)方法[6]，它将MAC法的特性引入到 level set方法中，计算时通过粒子来修正 level set函数，它捕捉到的交界面十分光滑，几乎无质量损失.为了加快计算速度，Enright等[7]提出了一种局部快速粒子level set方法——FPLS，该方法采用一阶精度的半Lagrangian格式[8]求解level set方程，用一阶精度fast marching技术[9]进行重新初始化，粒子的运算则采用二阶精度Runge-Kutta格式.

在实际应用中，复杂交界面需要高分辨率网格来模拟，采用均匀网格将消耗大量计算机内存，计算速度也将大大降低.Strain[10]在采用半 Lagrangian方法求解level set方程时，首先引入了树型结构的自适应网格，这种网格结构在交界面附近采用高分辨率网格，而在远离交界面的区域则保持较粗的分辨率.这样一方面提高了计算结果的精度，另一方面减少了无关区域所占用的内存.但该方法为了保持在 T型节点插值的连续性，重新初始化阶段在交界面附近区域采用三角网格[11]，计算量仍较大.2002年，Sochnikov等[12]将 fast marching技术应用到四叉树型结构的自适应网格中，使得计算量进一步减少.这种自适应level set方法是通过减小交界面附近网格尺寸来保证解的守恒性，可能会导致交界面周围的网格与最粗网格的尺寸相差很大，形成了过于复杂的树型结构.

笔者将树型结构的自适应性与 FPLS方法结合起来，提出一种改进的自适应 level set方法——SAFPLS，该方法在交界面附近能自动形成一个具有固定宽度的高分辨率网格带，并在该网格带内求解level set方程，进行重新初始化运算，且粒子始终包含在最小网格带内.该方法保留了自适应level set方法的优点，同时 FPLS方法的高精度性使得该方法无需在交界面周围采用过细的网格，这样在保证计算结果高精度的同时，计算速度更快，消耗内存更少.SAFPLS方法的具体步骤为：

(1)按照初始化 level set函数，生成在交界面附近加密的树型结构网格；

(2) 采用FPLS方法求解level set方程；

(3) 根据level set函数值重新调整网格；

(4) 返回第(2)步.

1 FPLS方法的基本原理

在 FPLS方法中，正负粒子被随机布置在交界面周围窄带中(初始时刻正值区的粒子为正粒子；反之为负粒子).每个粒子有各自的半径 rp，大小被限定在 最 小 值 rmin= 0 .1max ( Δ x, Δy )和 最 大 值 rmax=0.5max(Δ x,Δy)之间，其值可根据下列公式确定.

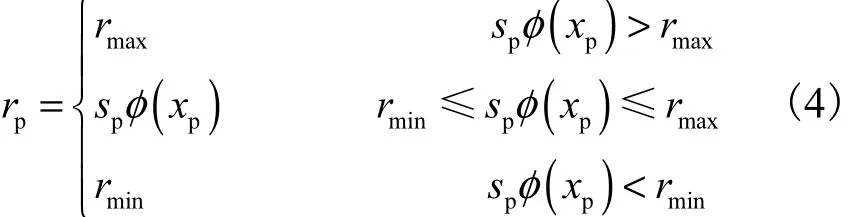
式中sp为粒子的符号(正粒子为+1，负粒子为-1).粒子的φ值将通过双线性或三线性插值得到.

这种确定半径办法的目的是使粒子尽量与交界面相切.当粒子穿过交界面达一个半径时，即认为是逃逸粒子.在剧烈变化的流场中，通过 level set方程得到的交界面附近的 level set函数值可能存在较大的误差.为了消除误差，可借助逃逸粒子来对 level set函数值进行修正.为此，定义一个与逃逸粒子有关的局部level set函数pφ，即

如果函数pφ和φ值不相等，说明level set方程得出的φ函数可能存在误差，取两者中绝对值较小的作为校正后的φ值.这种对φ的校正在重新初始化的过程中同样也需要.

当界面发生拉伸和断裂时，交界面附近网格粒子变得稀疏，需要补充粒子以确保追踪界面的准确性.而当非逃逸粒子远离交界面时，则需要将这些粒子删除.

在FPLS中，采用了一种低阶的半Lagrangian算法求解level set方程，该格式无条件稳定且收敛于真解.公式为

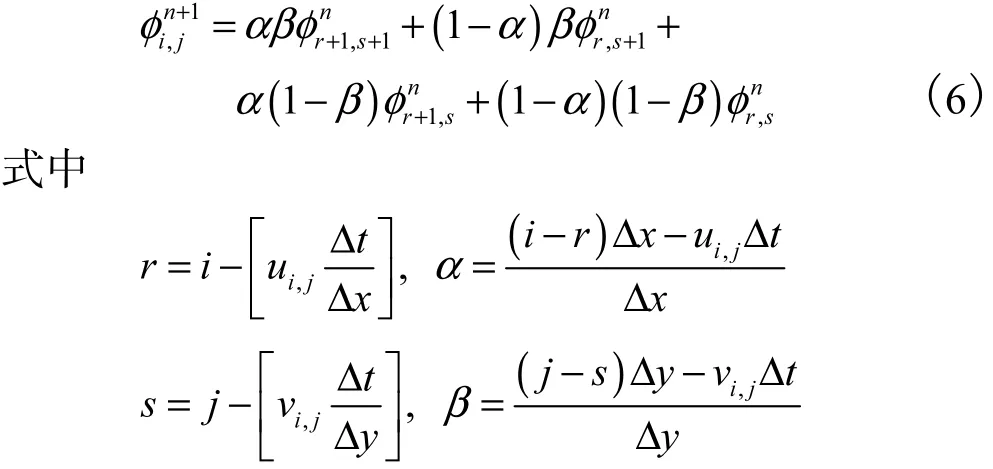
在进行重新初始化过程中，式(3)采用以下一阶迎风差分格式进行离散.

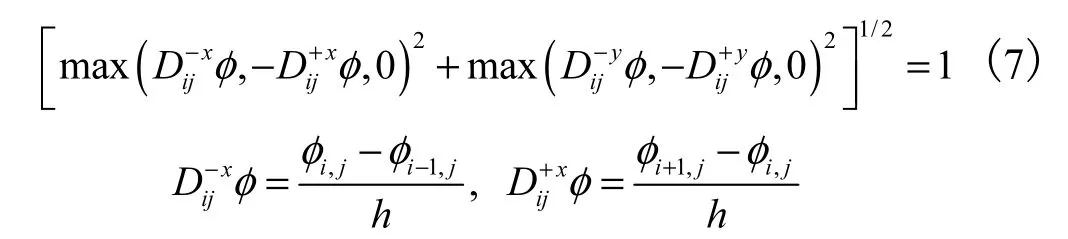
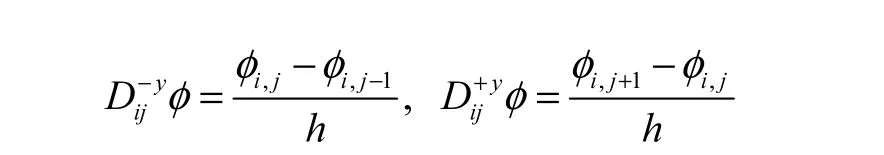
通过求解式(7)，式(3)的解可以快速地构造出来，这就是fast marching技术的主要思想，即从界面附近区域出发，逐步构造出Eikonal方程的解(见图1).

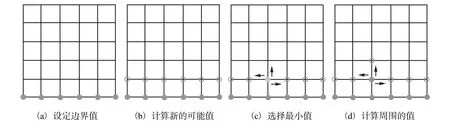
图1 采用快速步进法进行重新初始化Fig.1 Reinitialization with fast marching technique

2 SA-FPLS的原理

为简单起见，这里仅以二维的四叉树网格说明SA-FPLS的原理.三维的八叉树网格与之类似，不再赘述.在四叉树网格结构中，每个四叉树网格定义4个指向其子网格的指针(如果子网格不存在，指针指向空)和一个指向其父网格(如果父网格不存在，指针指向空)的指针，每个网格另有4个指向角点的指针和4个指向边的指针.每个节点有4个指针指向其相邻叶网格，对于特殊的节点，如T型节点，4个指针中有2个指向同一个网格.每个节点需要保存该节点的坐标及定义在该点的物理量.最粗的网格为 0层网格，略粗的为第1层，以此类推.图2中网格Ⅰ有4个子网格Ⅱ、Ⅲ、Ⅳ和Ⅴ和 4个节点 A、B、C 和 D，与子网格Ⅳ有共同节点C.网格Ⅳ有 4个子网格Ⅵ、Ⅶ、Ⅷ和Ⅸ和1个父网格Ⅰ.网格Ⅱ与网格Ⅲ共享1号边.节点E有4个指针分别指向网格Ⅱ、Ⅲ、Ⅳ和Ⅴ.在这种四叉树网格结构中，网格在每个方位上都有唯一的邻居，定义为与其相邻且层数不大于该网格的网格中层数最大的一个.如图3中网格Ⅱ与网格Ⅰ、Ⅳ、Ⅴ和Ⅵ相邻，但只有网格Ⅳ才是网格Ⅱ的邻居.

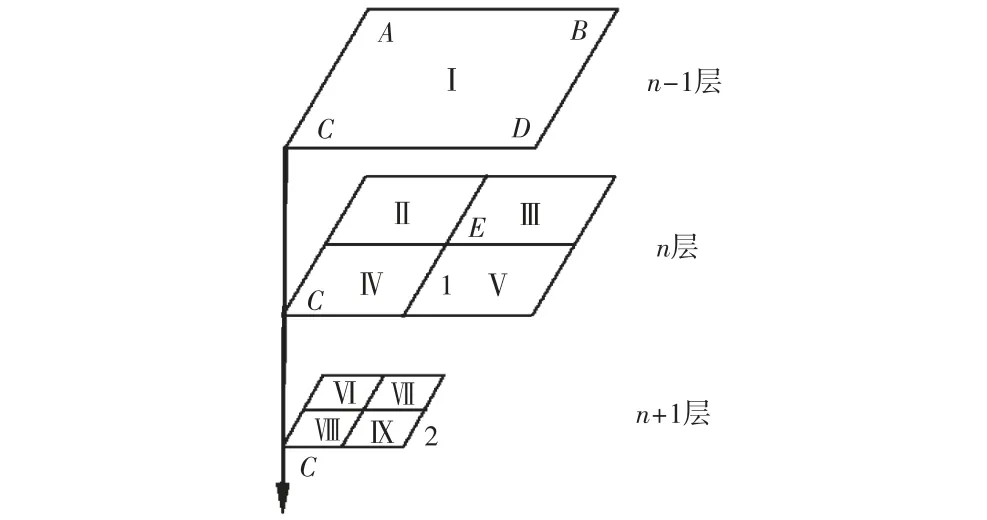
图2 树型网格结构Fig.2 Tree grid structure

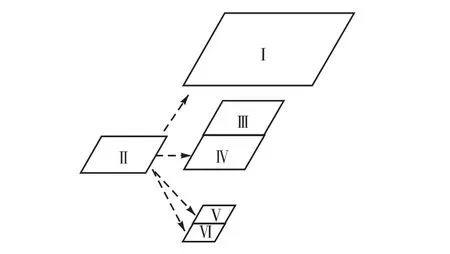
图3 网格及其邻居Fig.3 Given grid and its neighboring grid

在生成树型结构网格的过程中，首先分裂包含交界面的网格，若一个网格的角点上φ的符号相反，交界面必定穿越该网格，该网格即需要分裂，直至网格的层数达到规定的最大层数.因此，交界面附近的网格分辨率是最高的，那些与高分辨率网格相邻的网格也需要进行分裂，以保证高分辨率网格具有一定带宽.在交界面周围生成高分辨率的网格之后，还需要对网格进行平衡处理[13]，即保持相邻网格的大小相差不会超过 1倍.新产生的网格节点上的物理量通过线性插值得到.在计算过程中，为了提高交界面追踪精度，交界面附近的网格应始终保持高分辨率，且加密网格随着交界面的变化而变化.这样可以保证只在网格带内求解level set方程和进行φ值校正，同时防止因在交界面附近分裂网格时，线性插值导致的较大计算误差.因此，随着交界面的运动，需要在交界面附近将预先设定的高分辨率带的网格不断进行分裂，同时也要将脱离高分辨率网格带的网格进行合并(见图 4).

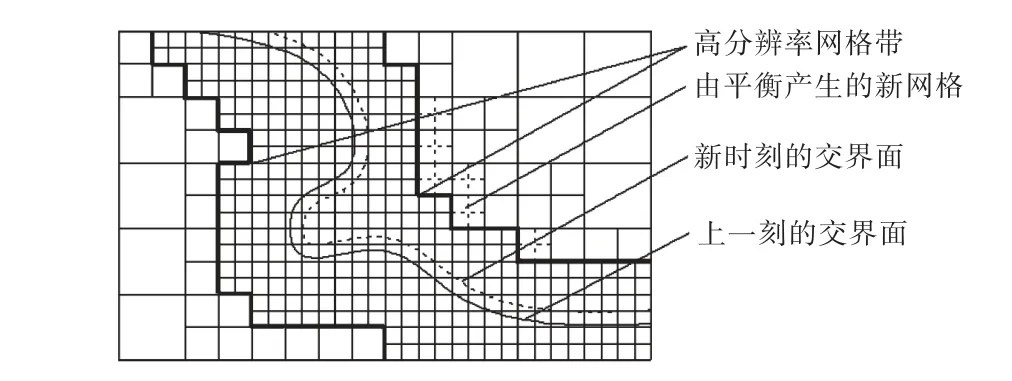
图4 交界面附近的高分辨率网格带Fig.4 Grid band of highest resolution around interface

在四叉树网格中采用半 Lagrangian方法求解level set方程与在均匀网格中有所不同，网格节点在上个时刻投影点的位置需要根据四叉树网格的结构寻找.首先，寻找投影点所在的 0层网格；然后，从该网格逐步向下找到投影点所在的子网格；最后，根据所在子网格角点上前一时刻的φ值，线性插值得到该节点新时刻的φ值.

在重新初始化的过程中，由于采用 fast marching技术，φ值是从交界面出发，迎风地向外构造得到，因此不会影响交界面的位置，当计算的某个节点的φ值大于高分辨率带的宽度时，向外构造过程即停止.值得注意的是，在向外构造的过程中，若遇到 T型节点时，则需要分裂该点周围所有层数小于规定最大层数的网格，以保证高精度网格带的宽度.

3 算例及分析

在二维算例中，采用如下一阶近似算法计算交界面的长度L，即

3.1 算例1

本算例模拟星型结构的扩张过程.交界面初始形状如图 5(a)所示，交界面以单位速度向向外法向扩张.计算区域大小为[0 ,2]×[0 ,2]，网格层数为4层，0层网格尺寸为0.04×0.04.初始level set函数表示为

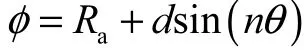
式中：Ra为平均半径；d为偏离Ra的距离；n为触角的个数；θ为半径与 x正向的夹角.在本算例中，Ra= 0 .3, d = 0 .2, n= 7 .图 5(b)是交界面分别在 0～0.05 s 6个时刻的界面位置.可以看出，界面在运动中始终保持与初始形状特征相似的形状，只是触角变得越来越厚.

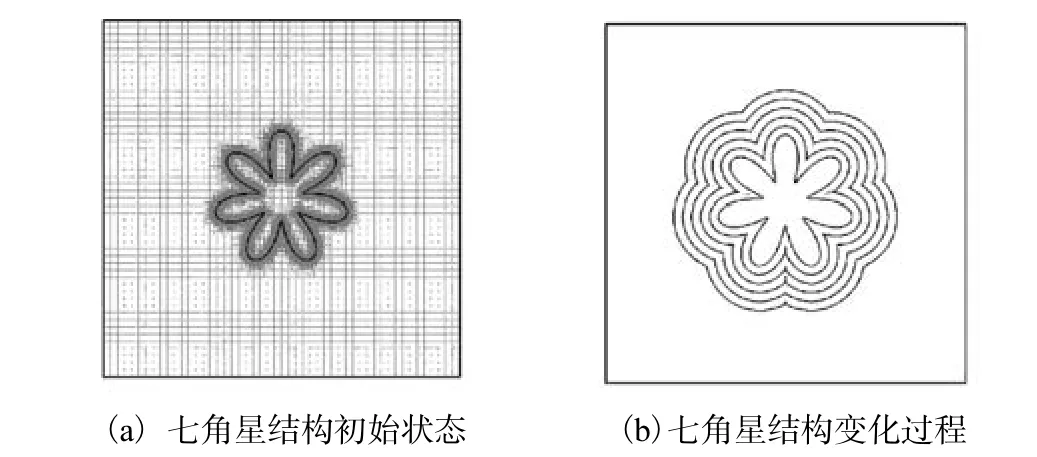
图5 七角星结构扩张过程的数值模拟结果Fig.5 Numerical results of expansion of seven-pointed star

3.2 算例2

本算例目的在于检验 SA-FPLS方法在剪切流场中对复杂交界面追踪的有效性.计算区域为[0 ,1]×[0 ,1]，网格层数为4层，0层网格尺寸为0.04×0.04，界面初始形状为一个半径为0.15、圆心在[0 .5,0.75]处的圆(见图6(a)).速度场表示为

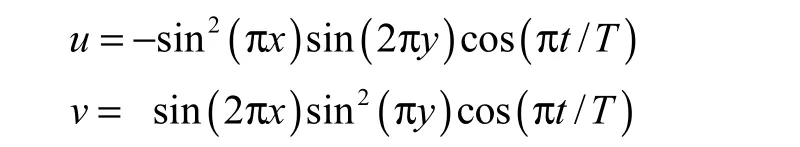
式中，流场周期T为8 s，时间步长为0.005 s.圆的变形过程如图 6所示.可见，由于在交界面附近采用了高分辨率的网格，尾部丝状结构保持得相当完整.同时，由于采用自适应网格，大部分区域保持较粗的网格，从而节约了大量内存和计算时间.

3.3 算例3

本算例模拟圆在1个有16个涡旋的流场中的变形情况.圆的初始状态及初始网格结构与算例 2一致，不同的是，该模型采用周期性边界条件，其周期性速度场[15]表示为

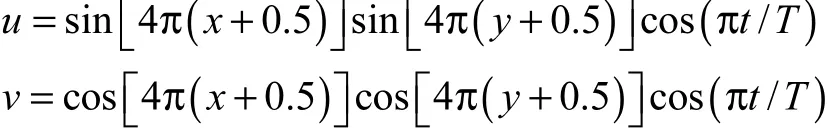
式中，流场周期T为2 s，计算时间步长为0.005 s.变形过程如图 7所示，在变形过程中，由于采用了周期性边界条件，交界面穿过计算区域上端后，又重新出现在计算区域下端，且上下边界的网格与节点保持一一对应.可以看出 FPLS与自适应网格相结合，可以适应十分复杂的流场结构.

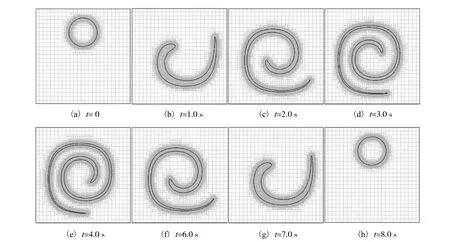
图6 圆在简单旋转流场中变形过程的数值模拟结果Fig.6 Numerical results of transformation of circle in single vortex flow

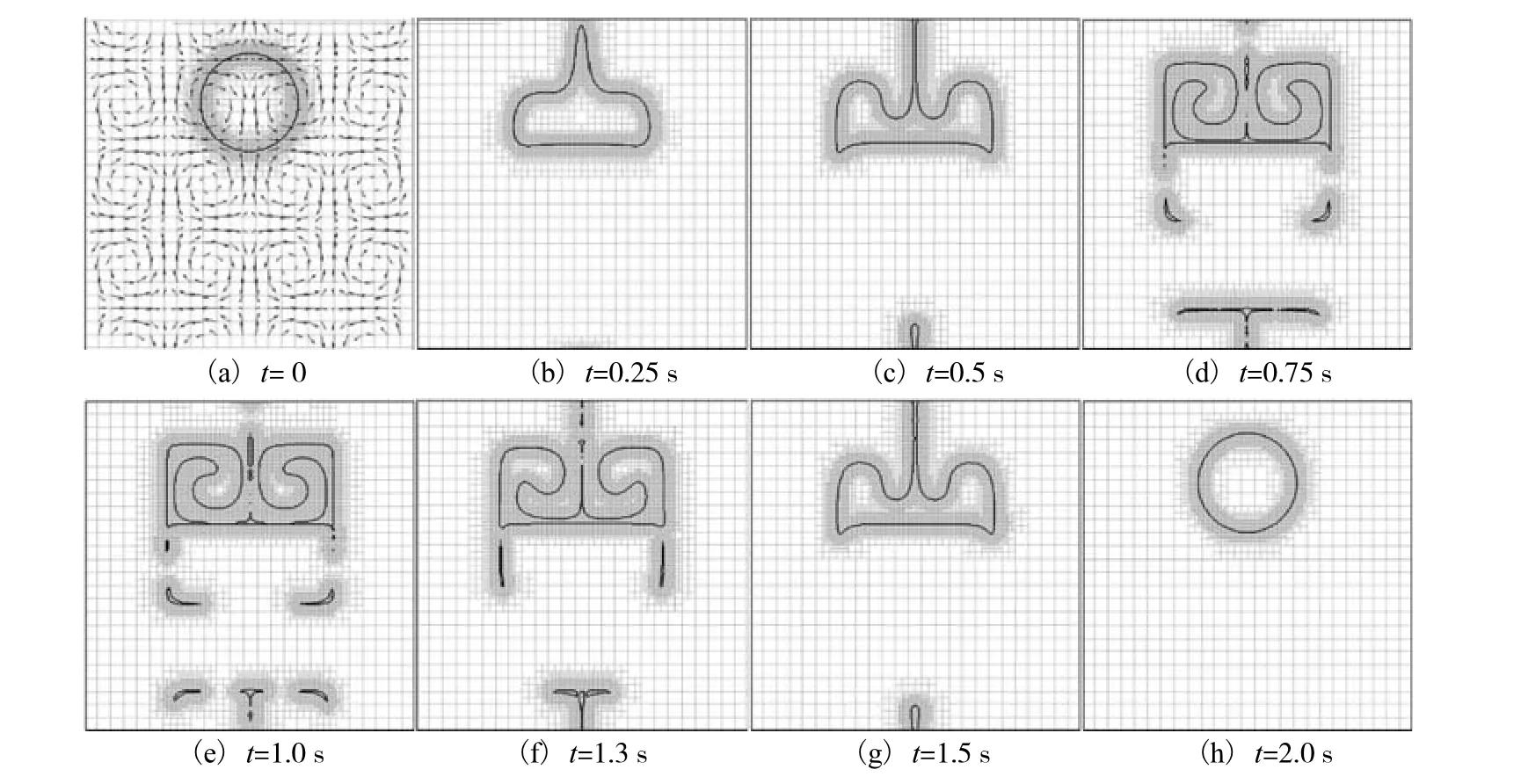
图7 圆在多涡流场中变形情况的数值模拟Fig.7 Numerical results of transformation of circle in multi-vortex flow

检验模型守恒性优劣的方法是对比初始时刻界面所围圆面积与 1个周期后界面恢复到原始形状后面积的差异.界面所围面积的计算式为

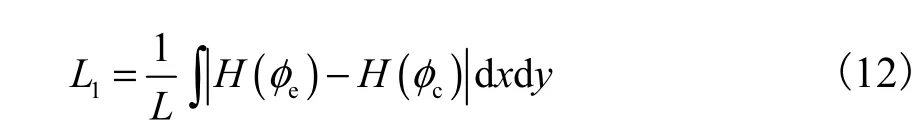
式中：L为交界面的期望长度；H为Heaviside函数；φe为真解；φc为计算结果.算例2和算例3计算结果的误差分析如表1所示.

3.4 算例4

算例4和算例5将讨论SA-FPLS方法在三维空间中的应用.算例4模拟一个半径为0.15的Zalesak圆球[16]在流场作用下的变化情况，球的初始位置为[0 .5,0.75,0.5]，切口的宽度为 0.05，深度为 0.125.计算区域尺度为[0 ,1] × [ 0 ,1] × [ 0 ,1]，网格层数为 4，最粗网格大小为0.0625× 0 .0625× 0 .0625，流场表示为

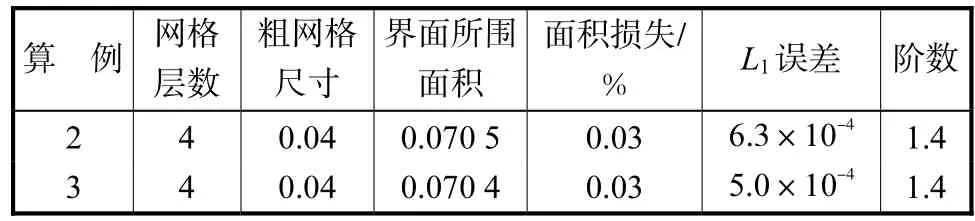
表1 计算结果的误差分析Tab.1 Error analysis of numerical results

计算时间为 2 s，时间步长为 0.005 s.界面运动过程如图 8所示，Zalesak圆球经过一个周期的运动后又回到初始位置，而缺口仍然保持尖锐.

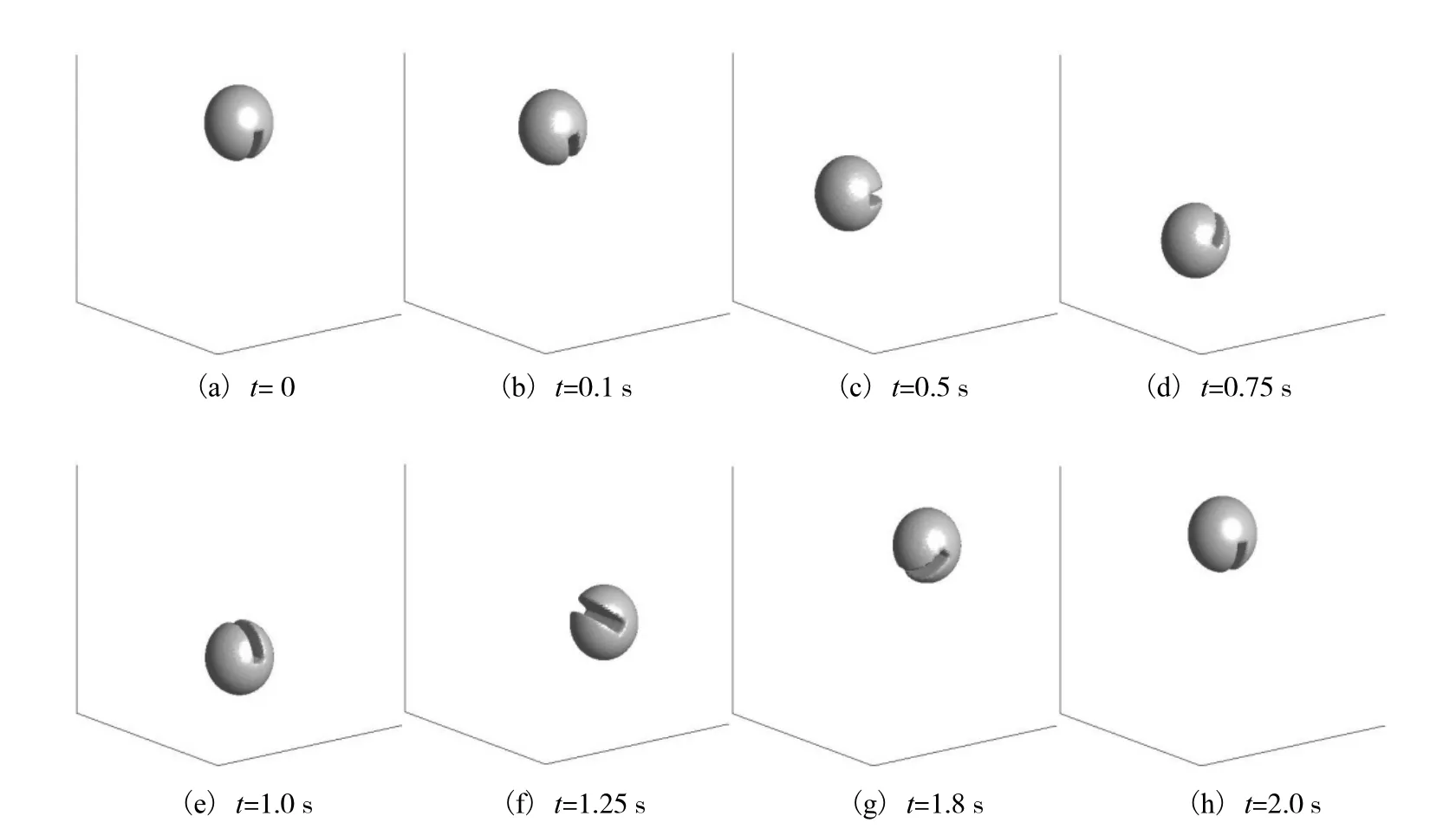
图8 Zalesak圆球的旋转过程数值模拟结果Fig.8 Numerical results of rotation of Zalesak sphere

3.5 算例5

本算例模拟一个半径为 0.15、初始位置为[0.35,0.35,0.35]的球体在三维流场作用下的变形过程，如图 9所示.计算区域为[0 , 1] × [ 0 , 1] × [ 0 , 1]，网格层数为 3，最粗网格大小为0.04× 0 .04× 0 .04.流场表示为式中，流场周期 T为 2,s，计算时间步长为 0.005,s.结果表明，圆球在1.0,s时达到最大拉伸后，又恢复到原样，而其中各图为圆球分别在 t为0～2.0,s时的形状.

4 结 语

将自适应网格与 FPLS结合起来，探讨了一种交界面追踪方法 SA-FPLS.从算例中可以看出，SAFPLS一方面继承了 FPLS的优点，交界面具有良好的光滑性，总体质量有良好的守恒性；另一方面由于它只在交界面附近窄带内求解level set函数，包括进行重新初始化，同时基于四叉树或八叉树的自适应网格只在交界面附近加密网格，而在远离交界面的区域保持较粗网格，因而这种方法既可节约内存，又可提高计算效率.

［1］Osher S，Sethian J. Fronts propagating with curvature dependent speed：Algorithms based on Hamiliton-Jacobi formulations[J].Journal of Computational Physics，1988，79(1)：12-49.

［2］Sussman M，Puckett E G，Osher S. A level set approach for computing solutions to incompressible two-phase flow[J].Journal of Computational Physics，1994，114(2)：146-159.

［3］Peng D，Merriman B，Osher S，et al. A PDE-based fast local level set method[J].Journal of Computational Physics，1999，155(2)：410-438.

［4］Sethian J. A fast marching level set method for monotonically advancing fronts[J].Applied Mathematics，1996，93(4)：1591-1595.

［5］Sussman M，Puckett E G. A coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two-phase flows[J].Journal of Computational Physics，2000，162(2)：301-337.

［6］Enright D，Fedkiw R. A hybrid particle level set method for improved interface capturing[J].Journal of Computational Physics，2002，183(1)：83-116.

［7］Enright D，Losassom F. A fast and accurate semi-Lagrangian particle level set method[J].Computers and Structure，2005，83(6)：479-490.

［8］Strain J. Semi-Lagrangian methods for level set equations[J].Journal of Computational Physics，1999，151(2)：498-533.

［9］Sethian J. Fast marching methods[J].SIAM Review，1999，41(2)：199-235.

［10］Strain J. Tree methods for moving interfaces [J].Journal of Computational Physics，1999，151(2)：616-648.

［11］Strain J. Fast tree-based redistancing for level set computations[J].Journal of Computational Physics，1999，152(2)：664-686.

［12］Sochnikov V，Efrim S. Level set calculations of the evolution of boundaries on a dynamically adaptive grid[J].International Journal for Numerical Methods in Engineering，2002，56(13)：1913-1929.

［13］Mark de B，Mark van K，Mark O，et al.Computational Geometry Algorithms and Applications[M]. Berlin：Springer，1999.

［14］Sussman M，Fatemi E. An efficient，interface-preserving level set redistancing algorithm and its application to interfacial incompressible fluid flow[J].SIAM Journal on Scientific Computing，1999，20(6)：1165-1191.

［15］Smolarkiewicz P. The multi-dimensional crowley advection scheme[J].Monthly Weather Review，1982，110(12)：1968-1983.

［16］Zalesak S. Fully multidimensional flux-corrected transport algorithms for fluids[J].Journal of Computational Physics，1979，31(3)：335-362.

Spatially Adaptive Fast Particle Level Set Method

HUANG Xiao-yun，LI Shao-wu
(School of Civil Engineering，Tianjin University，Tianjin 30072，China)

As an effective method of interface tracking，the level set method has been widely applied to surface tracking of single phase flow and interface tracking of multi-phase flow. The fast particle level set(FPLS)method，as an improved version of the level set method，not only is of relatively high accuracy in surface tracking，but also possesses high efficiency of calculation. By combination of the FPLS with tree-based adaptive gridding system，a spatially adaptive fast particle level set(SA-FPLS)approach is proposed，By solving the level-set equation with higher gridding resolution in a narrow mesh band around the interface，the solution accuracy can be further improved with less computer memory consumption and higher computational efficiency.

fast particle level set；adaptive grid；spatially adaptive fast particle level set

TV131.2

A

0493-2137(2010)11-0981-07

2009-09-02；

2010-05-14.

黄筱云（1980— ），男，博士研究生，td98298@sina.com.

李绍武，lishaowu@tju.edu.cn.