基于Gabor阶次跟踪的城市客车座椅振动特性分析

金 阳，郝志勇

(浙江大学能源工程学系，杭州 310027)

基于Gabor阶次跟踪的城市客车座椅振动特性分析

金 阳，郝志勇

(浙江大学能源工程学系，杭州 310027)

简要比较了目前主要的几种阶次分析技术的特点.将 Gabor阶次跟踪技术用于加速过程座椅振动响应信号的分析，先采用适当的参数对信号进行 Gabor变换得到时频谱图，接着对主要能量阶次进行时频遮罩，提取出相应的Gabor系数，然后用这些系数进行Gabor重构，得到阶次波形.从时域波形上的幅值峰值所在位置确定了座椅共振频率及相应发动机转速，提出了相应的减振措施.实际应用表明，Gabor阶次跟踪技术对于加速过程座椅振动响应信号的特征提取是有效的.

Gabor阶次跟踪；城市客车；座椅；振动

阶次跟踪(order tracking，OT)技术的发展有近20年的历史了，目前有基于硬件的阶次分析与基于软件(或数字)的阶次分析两大类.基于硬件的阶次分析是利用具有均匀角度间隔且与某轴同步旋转的编码盘产生的脉冲作为采样触发信号，直接得到等角度间隔的采集信号.码盘的分度越细，采样时钟的频率越高，测量精度越高.但受限于跟踪滤波器的成本及性能[1].而基于软件的阶次跟踪技术所用的原始采样信号都是时域等间隔的，它的实现方案主要有以下4种[2-5]：① 基于STFT的OT，它需要转速历程信号，可以对信号进行时-频表示，但不能进行阶次波形重构；② 基于角度域重采样的 OT，它需要转速脉冲信号，可对信号进行时间-阶次表示，也不能进行阶次波形重构；③ Vold_Kalman OT，它需要分度足够细的转速脉冲信号，不能对信号进行时-频表示，只能进行阶次分量的波形重构；④ Gabor OT (GOT)，它需要转速历程信息，可以对信号进行时-频表示，并可以进行阶次分量的波形重构.在以上4种方案中，Gabor是唯一能同时对信号进行时频表示与阶次波形重构的阶次分析方法，对于旋转机械的与转频相关的振动源与噪声源的判定是一种辅助手段.为此，笔者尝试将 GOT技术用于某城市客车座椅振动信号的分析，以期能提取出特征信息，为客车的减振降噪提供依据.

1 Gabor阶次跟踪的基本原理

Albright和 Qian等[6-8]于 2001年提出 Gabor阶次跟踪方法，它起源于 Gabor于 1946年提出的任何信号均可进行Gabor展开的思想.

对于信号s(t)，Gabor展开的表达式为

式中：T和Ω分别为时域和频域的采样步长；h(t)为Gabor基函数(Gabor elementary function)，它是在时域与频域上高度局部化的；,mnc 为 Gabor展开系数或Gabor系数.Gabor展开将信号表示成了具有不同时移与频率调制的Gabor基函数的加权和的形式.Bastiaans发现的Gabor系数与STFT之间的关系[9]为

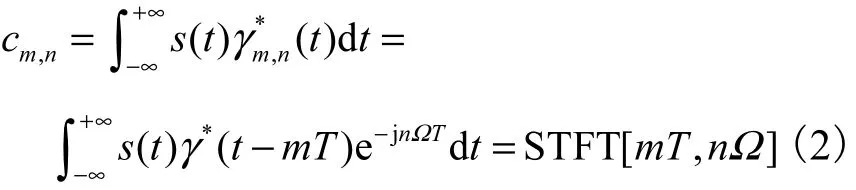
式(2)被称作Gabor变换式，γ(t)与式(1)中的h(t)互为对偶函数，γ(t)为分析窗函数，上标“*”表示复共轭， h(t)为合成窗函数，它们必须满足下面的关系

从以上的表达式可以看出，Gabor变换是可逆的，当经过 Gabor变换得到表示在时间-频率平面上的Gabor系数后，可以只选取与感兴趣的信号成分相关的那些系数来进行波形的重构(不仅仅限于对阶次成分进行重构)，而阶次跟踪就是在这一步中只选取代表某一阶次的Gabor系数，这就是Gabor阶次跟踪的基本思想.

基于离散 Gabor变换的阶次跟踪的关键步骤是对给定的合成窗h(k)、时间步长MΔ与频率区间数N求解对偶窗γ(k)，对偶窗γ(k)与h(k)的形状越相似，Gabor变换系数越能反映信号在时频采样点邻域内的时频特性[9].

2 Gabor阶次跟踪分析的流程

图 1为 Gabor阶次分析的流程图.在进行阶次波形重构前，要先对Gabor变换的谱图进行观察并调整分析参数，如窗长度、过采样率，以得到合理的反映信号时频特性的谱图，这有助于提高阶次信号的重构精度.

图1 Gabor阶次跟踪流程Fig.1 Flowchart of Gabor order tracking

图 2(a)为某测量信号 Gabor变换后谱图，横轴代表时间，纵轴代表频率，谱图中某点图案的色彩代表在该时刻、该频率下信号幅值的大小.图 2(b)是同步测量的转速曲线，图 2(c)则是由转速曲线及给定的带宽计算出的2阶时间-频率矩阵叠加在图2(a)上的结果.可以看出，图 2(a)中呈现的各类似于转速曲线的形状对应的正是不同的阶次.图 2(c)中黑色线所处位置在矩阵中为 1，而其他位置则为 0.此矩阵与原 Gabor变换系数阵相乘，就得到了与信号中的 2阶成分相对应的 Gabor系数，这个过程叫作时频遮罩(time-frequency masking).只对取出的这些系数进行Gabor展开，就得到了2阶时域波形.

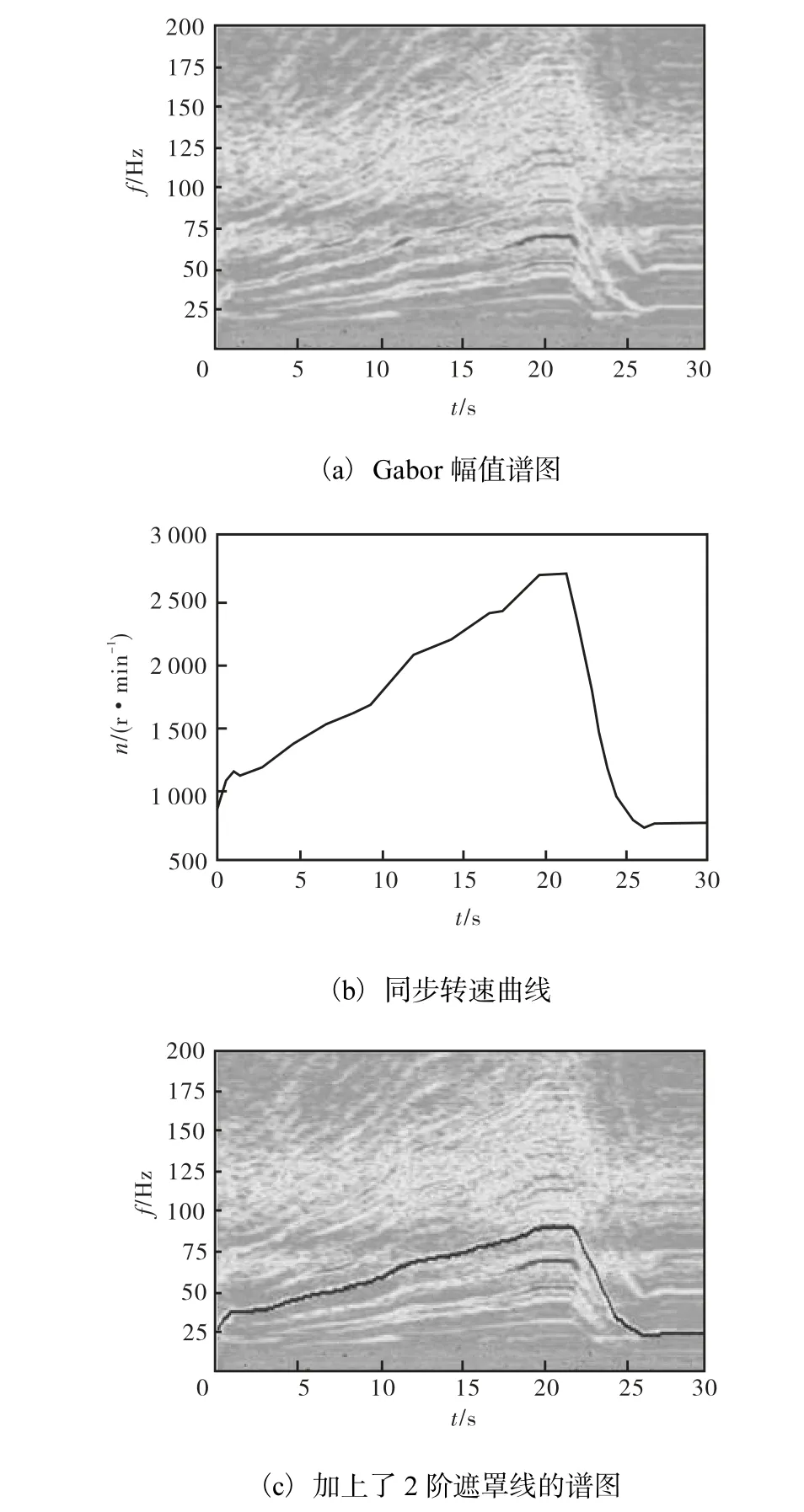
图2 时频遮罩示意Fig.2 Schematic diagram of time-frequency masking

3 客车座椅振动测试分析

3.1 测试工况

对处于试运行阶段的某混合动力(油电混合)大客车车内的前、中、后部的左右两侧各选了 2个座椅测量振动加速度信号，如图 3所示，测点编号从11～16.每个座椅下方的支撑横梁上安放 1个三向加速度计，共 18路信号.测量方向按图中定义，z轴垂直向上.该车装备直列 4缸四冲程发动机，发动机纵向后置，而辅助动力源电机水平横置，与变速箱间以锥齿轮接合，电机与发动机的转速比为 1.5(前者与后者之比).测量时，客车静止、空载、空档，发动机由怠速加速到2 700 r/min左右，采样频率2 048 Hz，测量时间30 s.

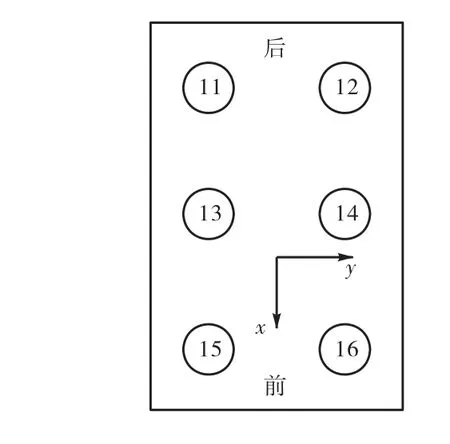
图3 座椅测点布置(俯视图)Fig3 Positions of measured seats (top view)

3.2 测试信号分析

图4是测点11～13的Gabor变换后的均方幅值谱图，单位为 dB，参考加速度值为 1×10-6,m/s2.为便于在图中定位各阶的位置，在图4中标出了3.5阶的位置.分析时采用的参数为：合成窗为高斯窗，窗长度为 2,048点，过采样率为 4，时频遮罩时的带宽为0.5阶.因为通过Gabor谱图发现，所有测点振动的主要能量均不高于 200,Hz，故图 4中只显示了200 Hz以下的图形.观察图 4中的各图形会发现：① 各阶次的曲线在转速上升段是清晰的，但在下降阶段有些许模糊现象，因为下降阶段的速度变化快，而分析窗长度是不变的，这是STFT的固有特征；② 多个测点的各阶次线均呈现出时亮时暗的现象，这说明这些阶次线穿越了多个共振带.从图 5、图 6中的 2个测点的时域波形上也可看出这一点.同一阶次线在不同测点位置、方向上最亮点的个数与位置有所不同，这是因为激励到每个测量自由度处的传递函数是不同的.在某个测量自由度上响应大的共振频率处，其他测量自由度上的响应可能很小.

本试验中所用发动机是没有平衡机构的直列 4缸四冲程柴油机，这种发动机对外的激振源有 2个：不平衡的二阶往复惯性力和由往复惯性力与气体压力共同产生的扭矩波动.它们通过动力系统的悬置传至车架、地板与座椅.各缸扭矩波动的合成结果是主要能量集中在 2、4、6…等主谐次或主阶次上，一般而言，主谐量的幅值随阶数的增大迅速减小.因而不论转速如何改变，2种激励的主要能量总可以按主阶次进行分解.二阶往复惯性力是随转速的平方递增的，作用于 z向；加速过程中主谐次扭矩波动幅值随油门增加的变化趋势也可近似认为是递增的.因此，4缸四冲程发动机加速过程的各阶次激励可看作是一个幅值渐增、频率渐增的扫频过程，即不存在幅值随转速增加发生突变的情形.但是振动响应的对应阶次波形随转速变化常表现出大的幅值波动，如图 5和图6中的响应点的主要能量阶次波形，因此响应中 对应阶次波形上的峰值就可判定为是由共振引起的.

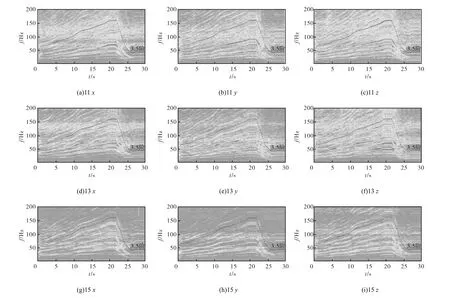
图4 部分测点Gabor变换谱图Fig.4 Gabor amplitude spectrograms of some signals

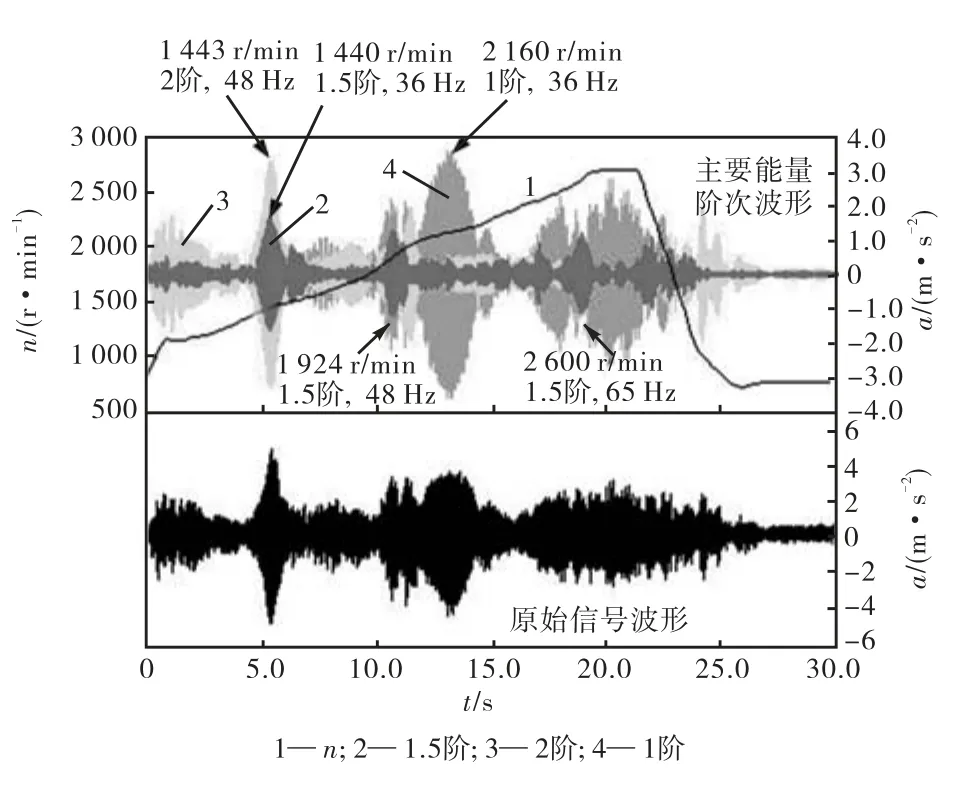
图5 测点16 y向的原波形及主要能量阶次波形Fig.5 Original waveform and significant order wave-forms of measurement point 16 y

综合利用各测点信号主要能量阶次的 Gabor波形重构，可以比较容易找到共振频率及对应的发动机转速.举例说明：图 5中主要能量阶次波形是从测点16的 y向提取出能量(指测量时段内阶次分量的总能量)最显著的前 3阶波形，显著性从低到高低次是1.5、2和 1.通过图 5可看出阶次波形重构提供了另一种看待测量信号组成的视角.它清晰地呈现了每一时刻(或转速)下各阶振动分量的贡献程度，还能揭示出有可能的阶次时域峰值重叠的情况.如图 5中转速为1,440,r/min左右的1.5阶与2阶成分会分别有36,Hz与48,Hz左右的共振，它们的叠加会使该点的振动加强.此外，从原时域波形很难看出峰值的地方通过阶次波形重构也可识别出共振频率，如图5中的1.5阶在1,924,r/min及2,600,r/min的峰值处分别对应的是48 Hz与65,Hz的共振频率，这可以从图6测点16的x向1.5阶次波形中得到验证，图6中的阶次能量显著性从低到高依次是1、1.5和2.

表 1是从各测点的主要能量阶次波形图中找出的共振频率及其相对应的发动机转速(仅列出了阶次波形的振动加速度峰值大于 0.2g的共振频率).在900,r/min、1,170,r/min、1,257,r/min、1,443,r/min、1,685,r/min、1,722,r/min、1,924,r/min、2,097,r/min、2,600,r/min和2,610,r/min等转速下，都会引起车厢内某些位置的座椅产生某些方向的共振.

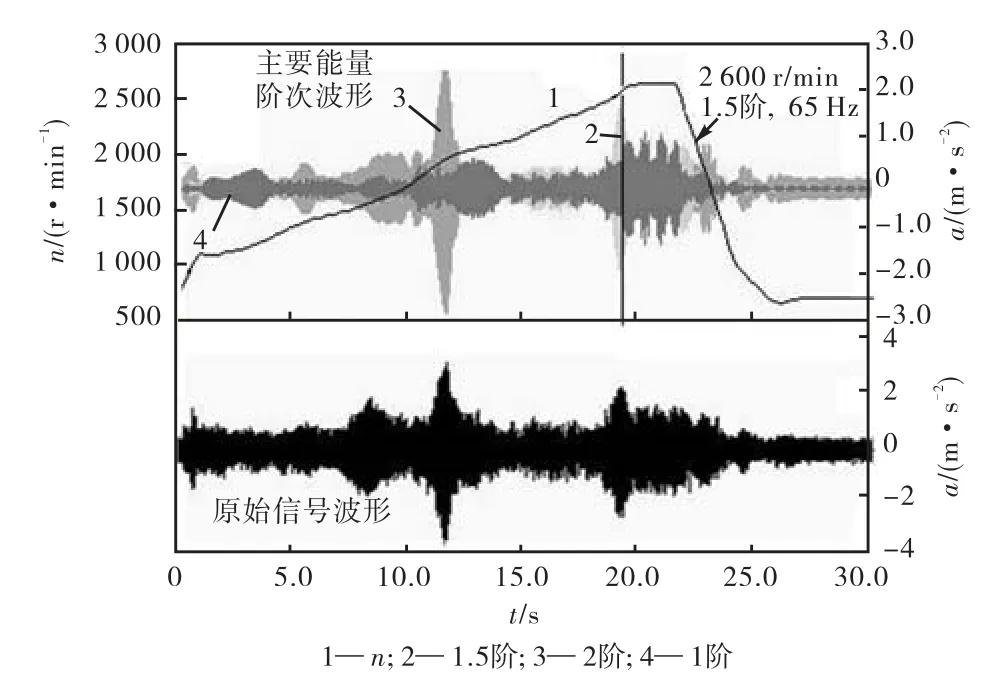
图6 测点16 x向的原波形及主要能量阶次波形Fig.6 Original waveform and the significant order wave-Fig.6 forms of measurement point 16 x

从表1中不难得出如下推论：

(1) 引起该车各测点振动的主要能量来自动力系统的 1阶、1.5阶、2阶与 4阶激励，且受 2阶影响的测点最多.2阶激励频率与该车装备的4缸四冲程发动机的发火频率及 2阶往复惯性力不平衡的特性是相吻合的.动力电机作为辅助动力源对振动的影响也体现了出来，1.5阶对应的正是动力电机的转频，它在转速大约高于 1,900,r/min后引起的振动开始显著，且主要引起 x向与 z向的振动，这与电机水平纵置的特点也是相吻合的.

表1 共振频率与各自由度上对应的转速Tab.2 Resonance frequencies and corresponding speeds at various degrees of freedom

(2) 该车各座椅振动的共振频率主要集中在30～90 Hz之间，并且比较密集.在发动机的工作转速范围内，共振频率完全处于主要阶次激励频率的覆盖范围内，因此难以找到一个降低全部座椅振动的转速段.

(3) 1,924,r/min应引起重视，它会同时引起除测点 11的 y向、测点 12、13、14的 z向、测点 15的 y向、测点16的y向和z向外的其他11个被测自由度上的共振.

加速行驶是城市客车运行中频率出现的工况，其振动水平对乘坐舒适性有很大影响.实验结果表明在该车发动机的工作转速段，会引起座椅结构的共振，恶化乘坐舒适性.提出的减振措施如下：

(1) 从改进客车动力系统的悬置设计入手，降低悬置高频段的动刚度.橡胶悬置在高频段，有动态硬化现象[10]，即动刚度加大，这会加大高频段的发动机激励向车身的传递.悬置的设计要兼顾的方面很多，要采用系统的优化方法.

(2) 改进座椅与车厢底板的连接设计，降低座椅结构的共振频率，使之移出发动机工作转速区内的主要能量阶次的频率范围.原车座椅支座与车厢底板为刚性连接，座椅与支座间也为刚性连接，车身的振动易于向座椅传递.

4 结 论

(1) Gabor阶次跟踪技术能实现信号的不同阶次成分在时域的分离或重构，同时还可将信号表示在时频面上，这是其他阶次跟踪技术所不具有的特性.在分离阶次信号前利用 Gabor变换的时频谱，有助于初步了解信号的时频分布特性、以及调整分析参数以得到时频面上尽可能清晰的阶次线.

(2) 用 Gabor阶次跟踪法分离出的阶次时域信号能确定不同转速下各阶次成分的贡献，定位共振频率甚至是振幅很微弱的共振频率，还能揭示出有可能的阶次时域峰值重叠的情况.

(3) 借鉴Gabor阶次跟踪的思想，还可拓展出基于Gabor变换／展开的其他应用领域，即分析对象不一定是旋转机械，时频遮罩时不一定是阶次曲线，而是针对具体的应用.

［1］赵晓平，张令弥，郭勤涛. 旋转机械阶比跟踪技术研究进展综述[J]. 地震工程与工程振动，2008，28(6)：213-219.

Zhao Xiaoping，Zhang Lingmi，Guo Qintao. Advances and trends in rotational machine order tracking methodology[J].Journal of Earthquake Engineering and Engineering Vibration，2008，28(6)：213-219(in Chinese).

［2］邱竣卿. Gabor时频与阶次分析探讨暨工程应用[D].台北，中国：国立中央大学，2004.

Chiu Chun-Ching. Investigation and Applications of Gabor Time-Frequency and Order Analysis[D]. Taipei，China：National Central University，2004(in Chinese).

［3］Pan Min-Chun，Chiu Chun-Ching. Investigation on improved Gabor order tracking technique and its applications[J].Journal of Sound and Vibration，2006，295(3/4/5)：810-826.

［4］Pan Min-Chun，Liao Shiu-Wei，Chiu Chun-Chin. Improvement on Gabor order tracking and objective comparison with Vold-Kalman filtering order tracking[J].Mechanical System and Signal Processing，2007，21(2)：653-667.

［5］汤宝平，何启源，魏玉果，等. 基于角加速度的复合计算阶次跟踪方法[J].机械工程学报，2008，44(8)：143-147.

Tang Baoping，He Qiyuan，Wei Yuguo，et al. Hybrid computed order tracking method based on angular acceleration[J].Chinese Journal of Mechanical Engineering，2008，44(8)：143-147(in Chinese).

［6］Albright M F，Qian S. A Comparison of the Newly Proposed Gabor Order Tracking Technique vs Other Order Tracking Methods[EB/OL]. http：//www. sandv. com/downloads/0306qian. pdf，2001-05-01.

［7］Qian Shie. Gabor expansion for order tracking[J]. Sound and Vibration，2003，37(6)：18-22.

［8］Shao H，Jin W，Qian S. Order tracking by discrete Gabor expansion[J]. IEEE Transactions on Instrumentation and Measurement，2003，52(3)：754-761.

［9］Qian Shie.Introduction to Time-Frequency and Wavelet Transforms[M]. Beijing：China Machine Press，2005.

［10］蒋开洪，徐 驰，上官文斌. 汽车动力总成悬置动态特性及悬置系统振动控制设计[J]. 汽车研究与开发，2005(10)：38-43.

Jiang Kaihong，Xu Chi，Shangguan Wenbin. Dynamic characteristic and vibration control design of a powertrain mounting system[J].Automobile Research and Development，2005(10)：38-48(in Chinese).

Gabor Order Tracking-Based Vibration Characteristics Analysis for City Bus Seats

JIN Yang，HAO Zhi-yong
(Department of Energy Engineering，Zhejiang University，Hangzhou 310027，China)

Characteristics of several predominant order tracking (OT) techniques were briefly compared. The Gabor order tracking (GOT) technique was used to analyze the run-up vibration signals from the seats of a city bus. The Gabor transformations with appropriate parameters were performed on the signals first to obtain the Gabor coefficient spectrum, and the spectrum was then time-frequency masked to extract the corresponding coefficients for the most significant orders. The order waveforms were then reconstructed with those coefficients. From the amplitude peak positions of the reconstructed time waveform，the seats’ resonance frequencies and the corresponding engine speeds were identified and the measures to reduce vibration were put forward. The real application shows that Gabor order tracking technique is effective for characteristics extraction of run-up vibration signals of city bus seats.

Gabor order tracking；city bus；seat；vibration

U467.1

A

0493-2137(2010)11-1009-06

2009-05-05；

2009-10-09.

湖北省自然科学基金资助项目(2005ABA305).

金 阳（1975— ），女，博士研究生，jin--yang@163.com.

郝志勇，haozy@zju.edu.cn.