环状旋转周期结构模态摄动分析

徐进友，刘建平，王世宇，宋轶民，秦 云

(1. 天津大学机械工程学院，天津 300072；2. 天津理工大学机械工程学院，天津 300384)

环状旋转周期结构模态摄动分析

徐进友1,2，刘建平1，王世宇1，宋轶民1，秦 云1

(1. 天津大学机械工程学院，天津 300072；2. 天津理工大学机械工程学院，天津 300384)

为揭示环状旋转周期结构的模态特性，以含附加结构的薄圆环为研究对象，采用直接模态摄动法建立了该周期结构动力特性近似解析方法，获得了环状旋转周期结构的模态表达式.给出了由附加结构的个数及振型的波数决定的固有频率分裂条件以及标准圆环振型与摄动振型之间的调制规律.研究表明：分裂的频率中余弦项频率值改变，而正弦项频率值保持不变；重根对应的振型被摄动振型的正、余弦项谐波调制，分裂根对应的振型仅余弦项振型被调制，且重根振型的调制程度大于分裂根振型.仿真结果证明了解析结论的正确性.

环状旋转周期结构；摄动法；固有频率分裂；模态调制

工程领域中广泛存在一类环状周期结构，该类结构被认为是在标准圆环上附加了周期结构而构成的旋转周期结构，如行星齿轮传动的内齿圈和电机的定、转子及水轮机的座环等.由于附加周期结构改变了原系统的轴对称性，系统的动力特性将发生明显的变化.因此对这类结构的振动研究具有理论和工程实用价值.

结构对称性的改变引起模态特性变化的现象引起了学者和工程技术人员的广泛关注.文献[1-5]运用不同方法研究了不对称圆环的振动特性.其中Allaei等[1]和 Detinko[2]分析了离散刚度支承下的圆环振动特性.Hwang和 Fox等[3-4]针对具有圆周方向轮廓变化的薄圆环，采用瑞利-里兹方法获得了频率和振型，分析了几何形状的变化导致的固有频率分裂现象.文献[5]利用拉普拉斯变换法研究了局部偏差对圆环振动模态的影响.

当附加结构的质量和刚度相对较小时，摄动法是分析周期结构动力特性的有效方法.楼梦麟等[6-7]采用模态摄动方法给出了复杂梁结构模态特性的近似解析解.Parker和 Mote[8-9]用摄动方法研究了盘振动的特征值.Kim 等[10]研究了周期分布结构对轴对称结构模态的影响，结果表明，由于结构中加入了周期结构而产生频率分裂现象，且振型由于附加谐波的调制而导致污染.Chang和 Wickert[11-12]以盘状结构为例，给出了固有频率分裂规则和模态污染规律.上述文献主要以盘状结构为研究对象，而环状旋转周期结构的模态污染特性未涉及.

由于产生固有频率分裂现象，结构的重频分裂为相近的 2个单频，相应的模态相互耦合，可以导致共振区加宽和振幅加大[13]，因此在结构的设计和应用中应考虑固有频率分裂的影响.笔者以工程中应用广泛的环状旋转周期结构为研究对象，采用摄动方法研究了该类结构的模态变化规律.

1 分析模型

不失一般性，基于环状周期结构的几何特点，建立图 1所示的分析模型.圆环的刚度和单位长度质量分别为EI和m，圆环半径为 r，截面积为 A.u和v分别为角 θ处的切向和径向位移.均匀分布在圆环内侧的周期子结构个数为 N(即周期数)，忽略几何形状的影响，将其简化为集中点，其刚度和质量分别为kt和 mt.

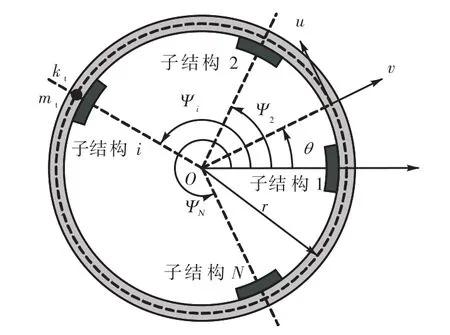
图1 旋转周期结构模型Fig.1 Model of rotationally periodic structure

2 基于摄动法的模态分析

2.1 固有频率分析

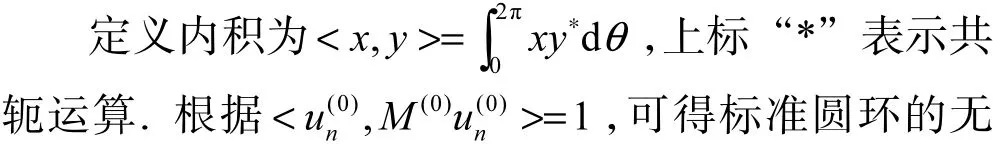
式中下标 c和 s分别表示特征值和振型的余弦项和正弦项.

式中余弦项为正号，正弦项为负号.显然，λΔ的取值与周期数N和波数n有关.

(1)若2n/N为整数，即

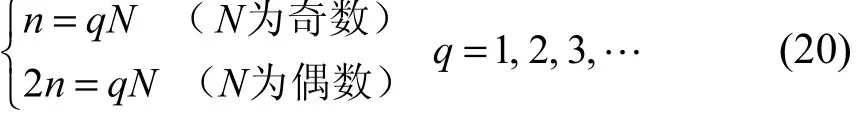
则c2NλΔ=，s0λΔ=，此时摄动特征值不等，即系统的固有频率发生分裂，系统的特征值可表示为

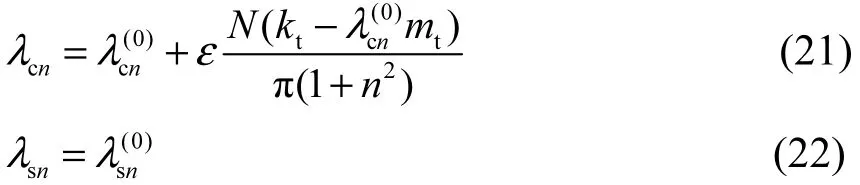
此时系统的1对重根分裂为2个互异的特征值，且仅余弦项特征值发生变化，而正弦项特征值保持不变.

(2)若 2n/N 不为整数，则 Δ λc= Δλs= N ，摄动特征值相等，即系统的固有频率仍为重根，系统的特征值可表示为

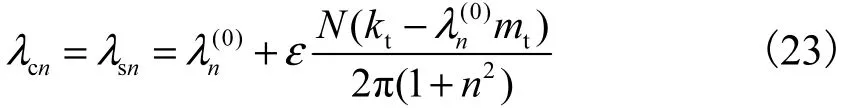
图 2给出了 N取不同值时Δλ随 n的变化规律.显然，若2n/N为整数，λΔ分裂为2个不等的值.例如，图2(a)为N ＝3，则在n为3的整数倍时，产生频率分裂，其余为重根.

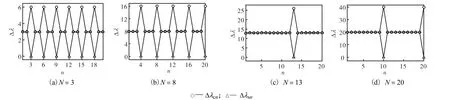
图2 Δλ随n的变化曲线Fig.2 Variety of Δλ with n

2.2 振型分析

旋转周期结构的摄动振型[10]为

由式(12)和式(24)～式(28)可得振型为

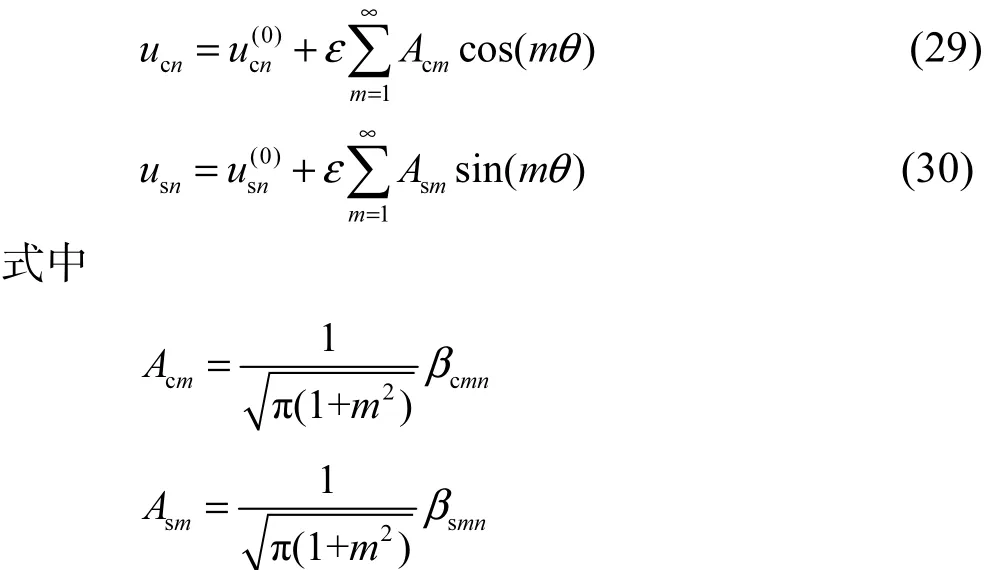
从式(29)和式(30)可以看出，系统的模态由2项组成，第1项为标准圆环的基本模态，第2项是由于增加了周期结构而产生的摄动模态.也即系统的模态是由圆环基本模态被摄动模态调制后得到的[7]，圆环的基本模态受到污染.摄动模态具有谐波的形式，其谐波系数Acm和Asm表明了模态的调制程度.

3 算例及分析

为验证本文结论，以含齿圆环为例，采用ANSYS软件进行仿真计算，参数取值见表1.

表1 含齿圆环的几何和物理参数Tab.1 Geometric parameters and physical properties of Tab.1 ring with teeth

图 3为固有频率随周期数 N的变化规律.图中N＝0表示无周期结构的标准圆环.从图 3中可以看出，在满足 2n/N为整数时，产生固有频率分裂，其余为重根.例如：对于 n＝3 时，则在 N＝1，2，3，6，··处发生频率分裂.对某一波数频率中分裂的 2个根，其中正弦项特征值近似等于标准圆环(N＝0)的值，余弦项特征值高于N＝0的值.

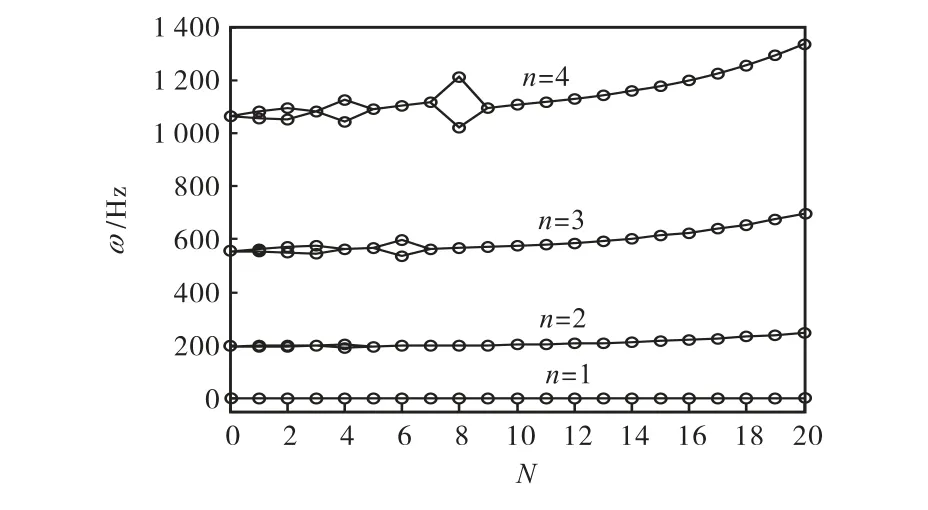
图3 固有频率随周期数的变化规律Fig.3 Variety of natural frequencies with periodic number

限于篇幅，振型分析仅以 N＝3为例.图 4给出了波数为 3和 4的模态.图 5为相应的振型谐波系数分布图.n＝3时系统特征值为分裂根，从图 5(a)可以看出，余弦项振型在 m＝3，6，9，··处存在谐波系数，而正弦项的谐波系数为 0，表明余弦项振型受到污染，而正弦项振型没有被污染.同理，从图 5(b)可以看出，若系统特征值为重根，则在 m＝1，2，5，7，8，10，··处存在摄动项，即基波被上述波数的谐波模态调制，且在 m＝1，7，10，··处，系数相同，在 m＝2，5，8，··处系数为相反数.从图 5(a)和图 5(b)的对比也可发看出，重根对应的摄动振型谐波项较多，调制程度大.

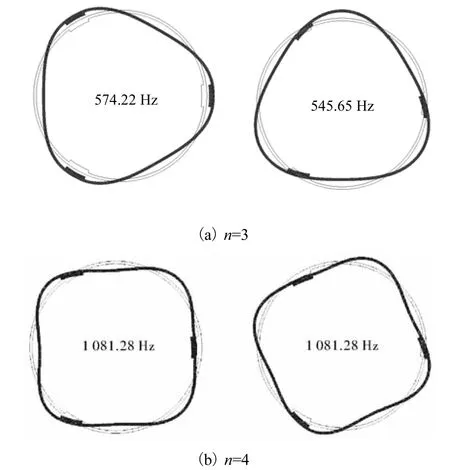
图4 N＝3的模态Fig.4 Mode for N＝3

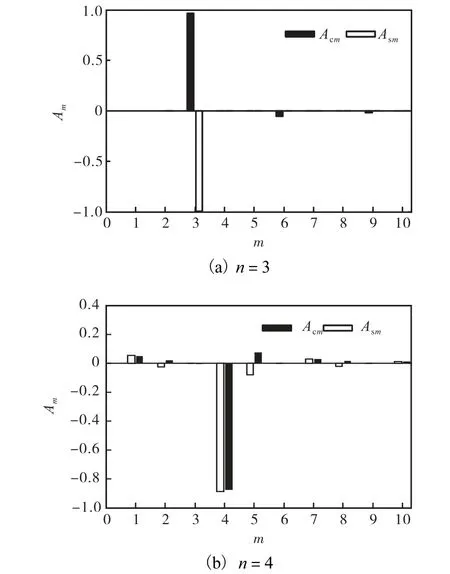
图5 N＝3的振型谐波系数Fig.5 Harmonic coefficients for N＝3 of mode shape

4 结 论

(1) 当周期数N与圆环振动的波数n满足2n/N为整数时，固有频率发生分裂.原对称结构的 2个频率中，余弦项频率值改变，而正弦项频率值保持不变.

(2) 当圆环振动的波数 n和附加周期结构的谐波数m满足|m±n|/N为整数时，圆环n波数振动的振型被附加周期结构的 m次谐波振型调制，且对重根振型的调制大于分裂根振型的调制.

(3) 特征值的变化特征对应振型的调制程度.重根对应的振型被摄动振型的正、余弦谐波调制；分裂根对应的振型仅余弦成分的振型被调制.

［1］Allaei D，Soedel W，Yang T Y. Natural frequencies and modes of rings that deviate from perfect axisymmetry[J].Journal of Sound and Vibration，1986，111(1)：9-27.

［2］Detinko F M. Free vibration of a thick ring on multiple supports [J].International Journal of Engineering Science，1989，27(11)：1429-1438.

［3］Hwang R S，Fox C H J，McWilliam S. The in-plane vibration of thin rings with in-plane profile variations(PartⅠ)：General background and theoretical formulation [J].Journal of Sound and Vibration，1999，220(3)：497-516.

［4］Fox C H J，Hwang R S，McWilliam S. The in-plane vibration of thin rings with in-plane profile variations(PartⅡ)：Application to nominally circular rings [J].Journal of Sound and Vibration，1999，220(3)：517-539.

［5］Park Han Gil，Lee Jang Moo，Kang Yeon June，et al. A study on the mode pair of a slightly asymmetric circular ring with multiple deviations[J].Journal of Sound and Vibration，2008，310(1/2)：366-380.

［6］楼梦麟，洪婷婷. 预应力梁横向振动分析的模态摄动方法[J]. 工程力学，2006，23(1)：107-111.

Lou Menglin，Hong Tingting. Mode perturbation method for lateral vibration analysis of prestressed beams[J].Engineering Mechanics，2006，23(1)：107-111(in Chinese).

［7］Lou Menglin，Duan Qiuhua，Chen Genda. Modal perturbation method for the dynamic characteristics of Timoshenko beams[J].Shock and Vibration，2005，12(6)：425-434.

［8］Parker R G，Mote C D. Exact boundary condition perturbation solutions in eigenvalue problems [J].Journal of Applied Mechanics，Transactions of the ASME，1996，63(1)：128-135.

［9］Parker R G，Mote C D. Exact perturbation for the vibration of almost annular or circular plates [J].Journal of Vibration and Acoustics，Transactions of the ASME，1996，118(3)：436-445.

［10］Kim M，Moon J，Wickert J A. Spatial modulation of repeated vibration modes in rotationally periodic structures[J].Journal of Vibration and Acoustics，Transactions of the ASME，2000，122(1)：62-68.

［11］Chang J Y，Wickert J A. Response of modulated doublet modes to travelling wave excitation [J].Journal of Sound and Vibration，2001，242(1)：69-83.

［12］Chang J Y，Wickert J A. Measurement and analysis of modulated doublet mode response in mock bladed disks[J].Journal of Sound and Vibration，2002，250(3)：379-400.

［13］邱家俊. 弹性体非线性振动多重共振的能量法[J]. 力学学报，1990，22(6)：753-758.

Qiu Jiajun. The energy method of multiple resonance in nonlinear vibration of elastic body[J].Chinese Journal of Theoretical and Applied Mechanics，1990，22(6)：753-758(in Chinese).

［14］刘习军，贾启芬. 工程振动理论与测试技术[M]. 北京：高等教育出版社，2004.

Liu Xijun，Jia Qifen.Engineering Vibration Theory and Testing Techniques[M]. Beijing：Higher Education Press，2004(in Chinese).

Modal Perturbation Analysis for Annular Rotationally Periodic Structures

XU Jin-you1,2，LIU Jian-ping1，WANG Shi-yu1，SONG Yi-min1，QIN Yun1
(1. School of Mechanical Engineering，Tianjin University，Tianjin 300072，China；2. School of Mechanical Engineering，Tianjin University of Technology，Tianjin 300384，China)

By taking a thin ring with additional structures as the research object，the approximate analytical method of dynamic characteristics and modal expressions of annular rotationally periodic structures were established by using direct modal perturbation method to reveal the modal characteristics of such structures. Natural frequency splitting conditions were defined by the number of additional structures and wave number，and the modulated rules between standard annular mode shape and perturbation mode shape were presented. The conclusions show that the cosineitem of the splitting doublet changes，while its sine item keeps invariant. Mode shape corresponding to the repeated doublet is modulated by sine and cosine harmonics of perturbation mode shape. Mode shape corresponding to splitting doublet is merely modulated by cosine harmonics. And the modulated degree of repeated doublet is greater than splitting doublet. Simulation results are well consistent with the analytical conclusions.

annular rotationally periodic structure；perturbation method；natural frequency splitting；mode modulation

TH113.1

A

0493-2137(2010)11-1015-05

2009-04-14；

2009-11-18.

国家自然科学基金资助项目（50705062）.

徐进友（1977— ），男，博士，xujinyou@tju.edu.cn.

王世宇，wangshiyu@tju.edu.cn.