非牛顿流体中在线气泡聚并的混沌特征

姜韶堃 ，马友光，范文元，杨 珂，朱春英

(天津大学化工学院化学工程联合国家重点实验室，天津 300072)

非牛顿流体中在线气泡聚并的混沌特征

姜韶堃 ，马友光，范文元，杨 珂，朱春英

(天津大学化工学院化学工程联合国家重点实验室，天津 300072)

利用光电信号采集系统测定了非牛顿流体中伴有聚并现象的在线连续上升气泡的通过频率信号，并采用基于相空间重构技术的混沌时间序列法对其进行了分析.相图和 Cao算法计算结果定性表明了非牛顿流体中伴有聚并现象的在线连续气泡上升行为具有混沌吸引子特征，服从确定性的混沌运动机理.最大 Lyapunov指数量化分析表明在线连续气泡上升行为的混沌特征与聚并程度密切相关：气泡行为的混沌程度随聚并程度增大而增大，增大气速易于导致气泡行为混沌程度增大.

气泡；聚并；非牛顿流体；相空间重构；最大Lyapunov指数

非牛顿流体中的气液两相流在气液接触、气液分离、气体吸收、沸腾、鼓泡塔、发酵和气蚀等众多领域广泛存在.由于非牛顿流体的流变特性，其中的气泡行为比在牛顿流体中更加复杂，例如气泡间的聚并过程.关于非牛顿流体中气泡聚并现象的研究报道较少.Acharya等[1]和 De Kee等[2-3]采用高速摄像机对黏弹性流体中气泡形状及气泡聚并过程进行了图像采集和实验研究.其后，Li等[4-5]和 Frank等[6]采用混沌理论分析了黏弹性流体中伴有聚并现象的气泡上升过程，得到其混沌运动特征.此外，Lin等[7-9]通过粒子图像分析仪测量了黏弹性流体中气泡聚并过程时的流线和剪切应力分布，分析了剪切变稀效应和黏弹性在聚并过程的作用.迄今，人们对非牛顿流体中的气泡聚并机理的认识还不是很清楚，更难以进行精确的理论描述.

对于非牛顿流体中在线连续气泡上升行为，在某一固定高度，由于气泡的不断聚并，连续气泡上升行为表现出明显的非周期特征，因此很难建立有效的理论预测模型.采用混沌时间序列分析研究非牛顿流体中在线连续气泡上升行为，是一种获得系统非线性动力学特性的有效途径.理论上，混沌是指确定的非周期行为，对初始条件具有很强的敏感依赖性.一般利用相空间重构方法，通过相图、庞加莱截面、关联维数、Kolmogrov熵和最大 Lyapunov指数等重要指标来定性和定量判断系统混沌行为.笔者主要分析了非牛顿流体中伴有聚并现象的在线连续气泡上升行为，鉴于过程的复杂性，采用不干扰流体流动的无接触式光电信号系统采集气泡通过频率信号，以相空间重构技术为基础，利用相图、最大Lyapunov指数等混沌时间序列分析指标进行了研究，讨论了非牛顿流体中伴有聚并现象的在线连续气泡上升行为的非线性混沌特征.

1 实 验

实验采用底部中央带有一个喷嘴(直径：1×10-3m)的方形有机玻璃槽(长×宽×高：0.15,m×0.15,m×1.50,m)作为气泡发生装置，槽内液面距喷嘴高度恒定为 1.10,m，如图 1所示，装置下方连接一个较大气室来抑制气泡生成过程引起的压力波动.调节转子流量计至适当气速，氮气泡通过喷嘴在槽内非牛顿流体中连续生成并不断上升.采用槽外光电信号采集系统对在线连续上升气泡进行信号捕捉，该系统主要由激光器、光电二极管、运算放大器以及数据采集卡组成，采样频率为 200,Hz.激光光束垂直于玻璃槽一侧壁面入射，穿过气泡上升轨迹，当气泡通过激光光束时，由于气泡表面的反射，只有部分光线通过气泡，位于玻璃槽另一侧的光电二极管接收该光强变化，并以电压形式表现出来，从而形成相应的脉冲信号.所有实验均在恒定室温297,K下完成.

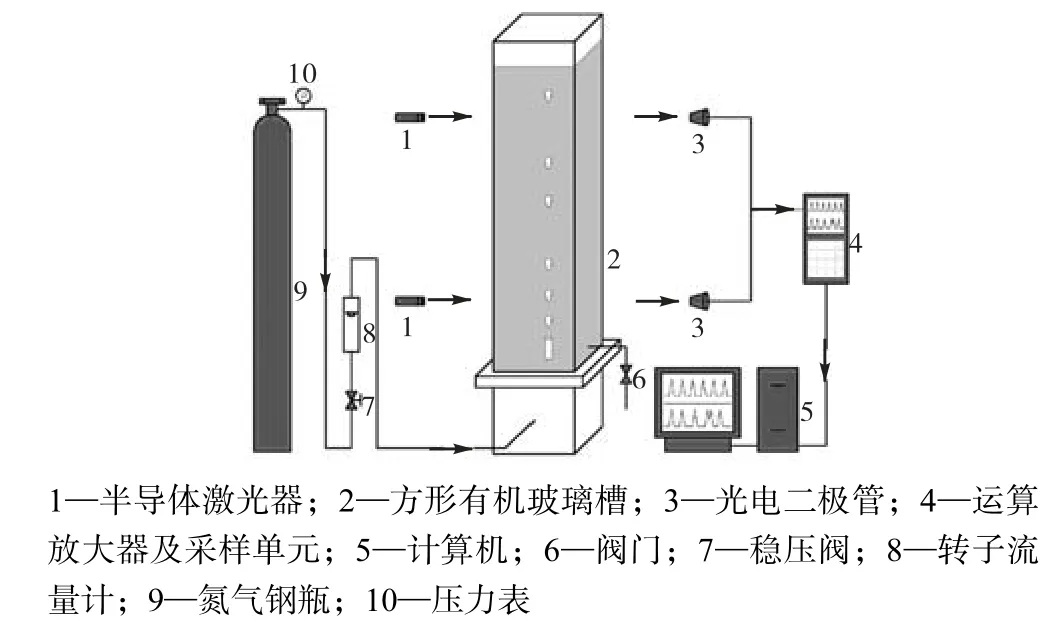
图1 气泡聚并实验装置示意Fig.1 Schematic representation of experimental apparatus Fig.1 for bubble coalescence

实验中采用的非牛顿流体的质量分数分别为1.0%、1.3%和1.6%的羧甲基纤维素钠(carboxymethylcellulose sodium，CMC)水溶液，其流变性质由 DV-III ULTRA PROGRAMMABLE RHEOMETER (Brookfield Engineering Laboratories，Inc.，U.S.A.)测定.从测定结果(见图2)可以看出，3种CMC水溶液的黏度均随着剪切速率的升高而降低，表现出明显的剪切变稀效应.

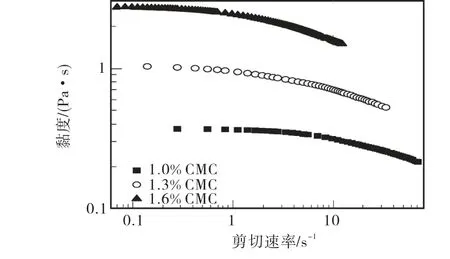
图2 黏度随剪切速率变化Fig.2 Variation of viscosity vs shear rate

2 混沌时间序列分析

在 3种 CMC水溶液中，气泡运动行为十分相似，因此仅以 1.0% CMC(质量分数)的实验结果为例进行分析.

首先采用双光束法和照相法分别估测了气泡上升速度和气泡体积.结果显示，气泡上升速度范围为0.20～ 0.40,m/s，气 泡 体 积 范 围 为 0.52×10-6～27.16×10-6,m3.按照文献[10]对气泡剪切速率的描述

式中：v表示气泡上升速度；deq表示气泡当量直径；VB为气泡体积.计算得到气泡上升剪切速率范围为10.54～25,s-1，恰好位于剪切变稀速率范围内.

图 3表示了不同位置的气泡通过频率信号片段.各个片段中都存在不同的信号脉冲，每一个脉冲都对应于一个单独通过的气泡.在喷嘴上方较低的位置，信号脉冲均匀密集，表示气泡的周期性上升过程；随着位置的升高，由于气泡聚并的发生，逐渐产生无规则的脉冲分布；当位置接近液面时，聚并频率大大降低，单位时间内气泡通过数量也明显减少，信号脉冲变得稀疏无序.

采用混沌时间序列分析方法来研究气泡通过频率信号的非线性动力学特性，最关键的步骤就是相空间重构参数的选择，包括时间延迟τ 和嵌入维数m.以图3中h＝0.3,m时的中信号为例，将实际测得的气泡通过频率信号归一化为均值为 0振幅为 1的时间序列xi，i＝1，2，…，N.图4显示出采用不同的τ对时间序列xi重构得到的二维相轨迹演变.当τ选择过小时，如图 4(a)所示，相轨迹都集中于对角线附近，数据之间关联程度太强，不易区分；当 τ选择过大时，如图 4(b)所示，相轨迹呈现出明显的折叠现象，数据之间毫不相关.因此，必须选择适当的 τ，使得重构的相空间既不线性相关，又非完全独立.去偏复自相关法[11]在实际信号处理上具有较好的鲁棒性，笔者采用该法计算τ.时间序列xi的m维去偏复自相关法存在基本关系为

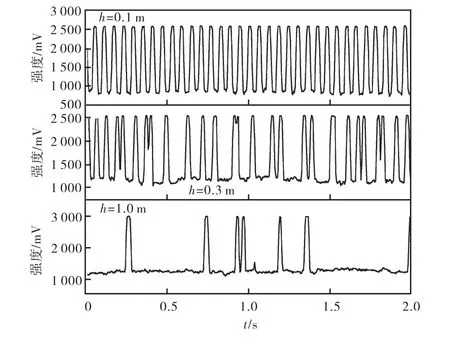
图3 气泡通过频率信号片段Fig.3 Part of frequency signal of bubble passage

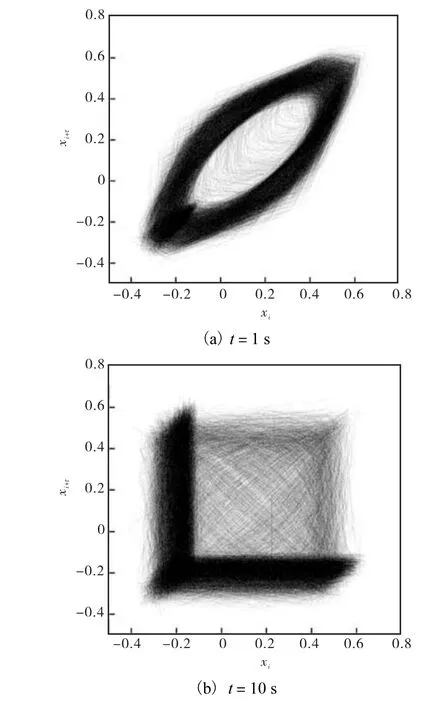
图4 不同时间延迟的相图Fig.4 Phase portraits with different time delays

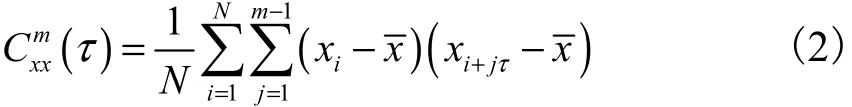
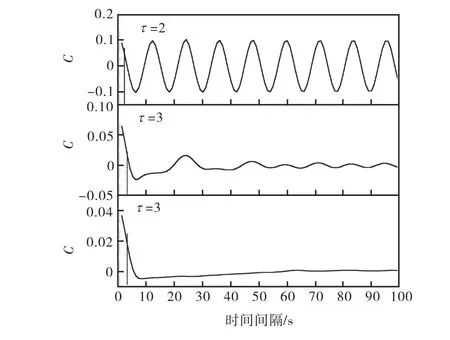
图5 去偏复自相关法计算结果Fig.5 Results of nonbias multiple autocorrelation method

对于嵌入维数 m的选择，已有大量文献报道采用 Cao算法[12-15]能够准确获得许多实际信号的m.其基本计算方法为

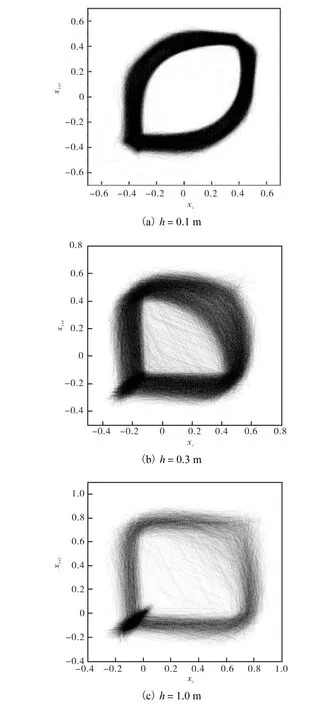
图6 不同位置的相图Fig.6 Phase portraits of different positions

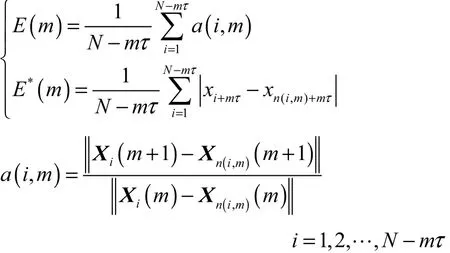
式中：Xi(m)表示实测气泡通过频率信号经相空间重构得到的向量(xi，xi+τ，…，xi+(m-1)τ)，i＝1，2，…，Nm；下标 n(i，m)(1≤n(i，m)≤N-mτ)使得 Xn(i,m)(m)是在按上述距离定义的 m维重构相空间中 Xi(m)的最近邻点.随着m的不断增大，当m增大到某一确定值时，E1(m)基本保持恒定，这时的 m 即为嵌入维数 m；若m 由小到大变化，E2(m)始终保持在 1左右，那么信号就是随机的；反之，就是确定性的.图7为采用Cao算法对气泡通过频率信号的计算结果.从图中可以看出，E2随着 m的增大并不是始终为 1，由此表明拟塑性流体中的气泡连续上升过程是确定性的，而非随机运动；此外，当E1趋于收敛时所对应的m值均比较大，而 m标志着能够足够描述相轨迹状态所需的最小相空间维数，即高气速条件下 CMC水溶液中气泡运动行为的系统自由度也比较大，与文献[16]中黏弹性流体低气速条件下的结果相比，气泡行为更加复杂.

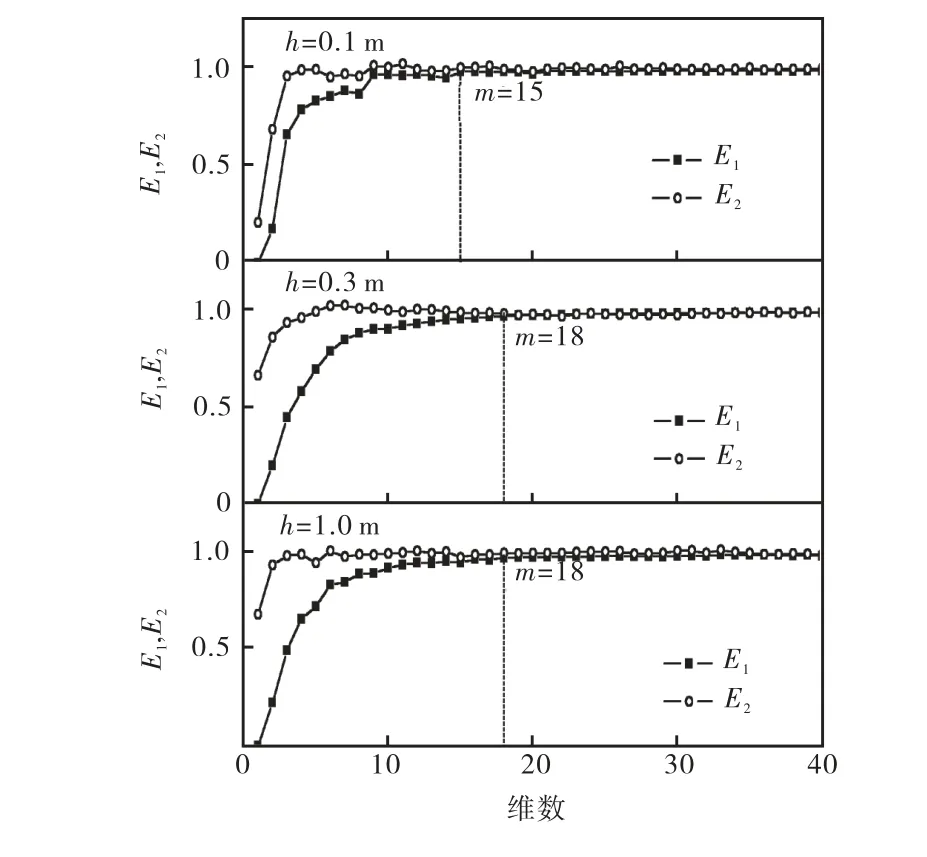
图7 Cao算法计算结果Fig.7 Results of Cao′s method

当τ和m确定后，即可通过Lyapunov指数量化气泡通过频率信号的混沌特性.在许多实际信号处理过程中，采用 Wolf法[17]能够有效地获得最大Lyapunov指数.首先在重构的相空间中选中初始基点 X(t0)及其最近邻点 X(t0′)，随着时间演化，当到达t1时刻，两点间距离由 L0变化为 L0′，并且L0′＞ε(ε＞0)，保留基点 X(t1)，重新选取与之夹角尽可能小的最近邻点 X(t1′)，使得两点之间距离 L1＜ε，继续上述演化跟踪过程，直到相轨迹终点，此时演化跟踪过程迭代次数为 M，则最大 Lyapunov指数λ1可表示为一般只要λ1大于 0，就可判断系统处于混沌状态；而对于周期运动，λ1小于或等于0.

表 1列出了不同气速条件下λ1随高度的分布.对于如Qg＝5×10-6m3/s、h＝0.1 m时的气泡运动行为，位置较低，气速较小，气泡生成间隔较大，气泡间存在线性相互作用，形成较均匀的气泡上升过程，因此λ1较小，接近于 0；随着气速增大，气泡生成间隔变小，气泡间相互作用逐渐由线性转变为非线性，破坏了气泡上升的周期性规律，形成非周期性上升过程，λ1明显增大.随着位置升高，不同气速条件下的气泡均加速上升，CMC水溶液的剪切变稀效应开始逐渐影响气泡行为：气泡通过后，局部黏度降低，使得下方气泡在局部阻力减小的情况下加速上升.受剪切变稀效应和先行气泡尾流等因素共同影响，气泡行为仍表现为非周期上升特征，甚至当位置升高到某一高度后，发生气泡聚并现象，气泡行为非周期特征加剧，λ1则表现出随着位置升高而增大，当位置继续升高，气泡频繁聚并，λ1达到最大值；随后，由于先前频繁聚并生成体积较大的新气泡，严重破坏了气泡原有的受力分布，使得气泡间非线性相互作用减弱，聚并频率大大减小，λ1明显减小.此外，随着气速增大，气泡生成间隔变小，上升速度增大，剪切速率增大，流体的剪切变稀效应促使气泡更易加速上升，在随后的上升过程中，更易强化非线性相互作用，导致聚并程度增大，从表 1中可以看出，气速增大更易得到较大的λ1.通常，由λ1的数值可以定量判断系统运动的混沌程度，表中 1所有条件下的λ1均大于 0，结合相图和Cao算法等定性分析，CMC水溶液中在线气泡上升过程表现为确定性的混沌运动，频繁聚并现象使得气泡行为混沌程度增大，而增大气速也易造成气泡运动混沌程度增大.

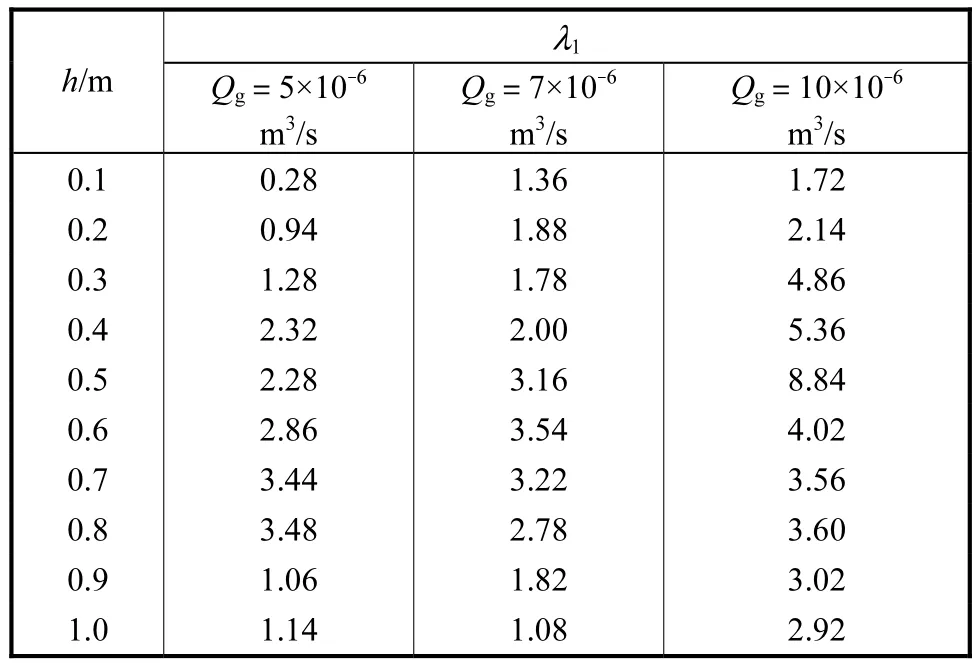
表1 不同气速条件下λ1随高度分布Tab.1 Variation of λ1 with height at different gas flowrates

3 结 论

利用光电信号采集系统测量了非牛顿流体 CMC水溶液中在线连续上升气泡的通过频率信号，采用基于相空间重构技术的混沌时间序列分析方法对该信号进行了分析，得到如下结论：

(1) 相空间重构二维相图清晰地显示，伴有聚并现象的在线气泡连续上升行为表现出明显的混沌吸引子特征.

(2) Cao算法计算结果表明，CMC水溶液中的在线气泡上升过程具有较高的系统自由度，是一个复杂的确定性非随机过程.

(3) 最大 Lyapunov指数均大于 0，表明了 CMC水溶液中在线气泡连续上升行为的混沌特征.

(4) 由最大Lyapunov指数定量描述的气泡行为混沌程度与气泡聚并程度密切相关，前者随后者增大而增大，相同高度下，增大气速导致气泡行为混沌程度增大.

［1］Acharya A，Ulbrecht J. Note on the influence of viscoelasticity on the coalescence rate of bubbles and drops[J].AIChE Journal，1978，24(2)：348-351.

［2］De Kee D，Chhabra R P，Dajan A. Motion and coalescence of gas bubbles in non-Newtonian polymer solutions[J].Journal of Non-Newtonian Fluid Mechanics，1990，37(1)：1-18.

［3］Dekee D，Chan M，Fong C F，et al. Bubble shape in non-Newtonian fluids[J].Journal of Applied Mechanics，2002，69(5) ：703-708.

［4］Li H Z，Frank X，Funfschilling D，et al. Bubbles′ rising dynamics in polymeric solutions[J].Physics Letter A，2004，325(1)：43-50.

［5］Li H Z. Bubbles in non-Newtonian fluids：Formation，interactions and coalescence[J].Chemical Engineering Science，1999，54(13/14)：2247-2254.

［6］Frank X，Li H Z. Route to chaos in the rising dynamics of a bubble chain in a polymeric fluid[J].Physics Letter A，2008，372(40)：6155-6160.

［7］Lin T J，Lin G M. The mechanisms of bubble coalescence in a non-newtonian fluid[J].The Canadian Journal of Chemical Engineering，2003，81(3/4)：476-482.

［8］Lin T J，Lin G M. An experimental study on flow structures of a single bubble rising in a shear-thinning viscoe-lastic fluid with a new measurement technique[J].International Journal of Multiphase Flow，2005，31(2)：239-252.

［9］Lin T J，Lin G M. Mechanisms of in-line coalescence of two-unequal bubbles in a non-Newtonian fluid[J].Chemical Engineering Journal，2009，15(3)：750-756.

［10］林嘉宇，王跃科，黄芝平，等. 语音信号相空间重构中时间延迟的选择：复自相关法[J]. 信号处理，1999，15(3)：220-225.

Lin Jiayu，Wang Yueke，Huang Zhiping，et al. Selection of proper time-delay in phase space reconstruction of speech signals[J].Signal Processing，1999，15(3)：220-225(in Chinese).

［11］Ma H G，Han C Z. Selection of embedding dimension and delay time in phase space reconstruction[J].Frontiers of Electrical and Electronic Engineering in China，2006，1(1)：111-114.

［12］Cao Liangyue. Practical method for determining the minimum embedding dimension of a scalar time series[J].Physica D：Nonlinear Phenomena，1997，110(1/2)：43-50.

［13］Kumar U，Prakasha A，Jain V K. Characterization of chaos in air pollutants：A Volterra-Wiener-Korenberg series and numerical titration approach[J].Atmospheric Environment，2008，42(7)：1537-1551.

［14］Wang J，Sun L，Fei X Y，et al. Chaos analysis of the electrical signal time series evoked by acupuncture[J].Chaos，Solitons and Fractals，2007，33(3)：901-907.

［15］Li X L，Ouyang G. Nonlinear similarity analysis for epileptic seizures prediction[J].Nonlinear Analysis：Theory，Methods and Applications，2006，64(8)：1666-1678.

［16］Li H Z，Mouline Y，Choplin L，et al. Chaotic bubble coalescence in non-Newtonian fluids[J].International Journal of Multiphase Flow，1997，23(4)：713-723.

［17］Wolf A，Swift J B，Swinney H L，et al. Determining Lyapunov exponents from a time series[J].Physica D：Nonlinear Phenomena，1985，16(3)：285-317.

Chaotic Characteristics of in Line Bubble Coalescence in Non-Newtonian Fluid

JIANG Shao-kun，MA You-guang，FAN Wen-yuan，YANG Ke，ZHU Chun-ying
(State Key Laboratory of Chemical Engineering，School of Chemical Engineering and Technology，Tianjin University，Tianjin 300072，China)

The frequency signal of continuous rising bubbles with coalescences in non-Newtonian fluid was measured by means of a photoelectrical signal collection system and analyzed using chaotic time series analysis based on the phase space reconstruction. The results of phase portrait and Cao's method show qualitatively that the in-line continuous bubble rising behavior with coalescence in non-Newtonianfluid follows a deterministic and chaotic motion mechanism with the characteristics of chaotic attractor. The largest Lyapunov exponents quantify that the chaotic characteristics of the in-line continuous bubble rising behavior are closely related with the coalescence degree. The chaotic degree of bubble behavior increases with the coalescence degree and increasing the gas flowrate tends to increase the chaotic degree of bubble behavior.

bubble；coalescence；non-Nnewtonian fluid；phase space reconstruction；largest Lyapunov exponent

TQ021

A

0493-2137(2010)11-1025-06

2009-08-24；

2010-06-23.

国家自然科学基金资助项目(20476073)；化学工程联合国家重点实验室课题(SKL-ChE-08B03).

堃姜韶 （1980— ），男，博士，j_sk45@yahoo.com.cn.

马友光，ygma@tju.edu.cn.