求解背包问题的基因属性保留遗传算法

马丰宁，谢 龙，郑 重

(天津大学管理学院，天津 300072)

求解背包问题的基因属性保留遗传算法

马丰宁，谢 龙，郑 重

(天津大学管理学院，天津 300072)

遗传算法是解决大规模背包问题的有效方法，在研究几种有效的遗传算法求解背包问题基础上，注意到遗传算法的进化代数对求解结果的影响大于群体规模，保持基因位数据的有效性，对进化效率有重大影响.提出了基因属性保留遗传算法(attribute gene-reserved genetic algorithm，AGGA)，将每一位基因的属性差异，在不同代遗传中加以保留，结合精英保留方法，很好地解决了提前收敛、GA欺骗问题，从很少的群体出发，就可以达到好的结果，实证了AGGA对背包问题的高效性，得到好于参考文献的结果，并构造了150个物体的背包问题实例.

遗传算法；简单群体；基因属性保留；精英保留策略；背包问题

背包问题(knapsack problem，KP)是计算科学中的一类非常经典的NP-hard问题.对该问题的研究既有理论价值，又有实际应用背景，如项目选择、投资组合、资源分配和货物装载等.求解 0-1背包问题的方法有许多种，由于该问题的解空间规模同问题规模呈指数关系，用动态规划、回溯法、分支限界法等确定性算法不适合求解规模较大的 0-1背包问题[1-3].遗传算法作为一种优化算法，在大规模 0-1背包问题的求解上得到有效的应用，并有多种改进算法，如贪心算法[4]、佳点集算法[5]和主动进化算法[6]等.

目前各种改进的遗传算法，是对交换、选择和变异方法的改进，这些改进确实在提高算法效率上成果很大[7].笔者在研究各种有效的遗传算法求解背包问题基础上，注意到遗传算法的进化代数对所述结果的影响大于群体规模，保持基因位数据差异的有效性，对进化效率有重大影响[8-12].

笔者在对诸多不同遗传算法深入研究基础上，通过大量试验提出基因属性保留遗传算法(attribute gene-reserved genetic algorithm，AGGA).通过实例可以证明，设背包数量为n(即染色体的串长为n)，取初始群体容量为 L = 2 n，迭代次数取 K = 4 n，本算法可以得到好的效果.

1 改进的算法(AGGA)

KP问题的一般提法为：已知n个物品的容积及价值分别为 wi和 ci(1 ≤i≤n)，背包的最大容量限制为M，如何选择物品装入背包，使得在背包最大容量限制之内，所装入的物品的总价值最大，其严格的数学描述为新一代群体保留上一代的最佳解的选择策略，称为精英保留策略.

在以上定义的基础上，AGGA具体实现方法描述如下：

(3) 输出前 2L 项，比较结果(有时不同样本可以得到相同最优解)，结束.

以上算法有如下优点：算法简洁，保持优化结果的群体优势，避免提前收敛，进化效率高.

(1) 步骤1基因属性保留群体，能很好解决GA欺骗问题，其实质是对染色体编码的一种修正过程，这种修正是每1位染色体都得有差异特征，从而避免在进化中有某位染色体缺少差异而导致不能继续进化.

(2) 步骤3简单群体能够保持非冗余性，解决早熟问题，GA早熟的本质特征是指群体中的各个个体非常相似，导致搜索结果的不优.

(3) 步骤 5中，使用精英保留的策略，保留了进化的优势群体，而不仅是一个第t代的最优解.本文方法保留了前 2L 个个体，这将大大提高进化效率.

2 实 证

为了比较 GGA[4]算法与 AGGA算法在求解 KP问题时表现出的不同性能，下面给出了3个KP问题实例，其中实例 1、2取自文献[4]，该实例是一个被广为引用的著名的问题实例，常用它来比较演化算法的优劣；另一个关于150个物品的实例是按前2个实例的数据构建的.

1)KP问题实例1(50个物品)

物品的价值集C ＝{220，208，198，192，180，180，165，162，160，158，155，130，125，122，120，118，115，110，105，101，100，100，98，96，95，90，88，82，80，77，75，73，72，70，69，66，65，63，60，58，56，50，30，20，15，10，8，5，3，1}.

物品的容积集W ＝{80，82，85，70，72，70，66，50，55，25，50，55，40，48，50，32，22，60，30，32，40，38，35，32，25，28，30，22，25，30，45，30，60，50，20，65，20，25，30，10，20，25，15，10，10，10，4，4，2，1}，背包的最大容量1,000，规模为d＝50.

2)KP问题实例2(100个物品)

物品的价值集C ＝{597，596，593，586，581，568，567，560，549，548，547，529，529，527，520，491，482，478，475，475，466，462，459，458，454，451，449，443，442，421，410，409，395，394，390，377，375，366，361，347，334，322，315，313，311，309，296，295，294，289，285，279，277，276，272，248，246，245，238，237，232，231，230，225，192，184，183，176，174，171，169，165，165，154，153，150，149，147，143，140，138，134，132，127，124，123，114，111，104，89，74，63，62，58，55，48，27，22，12，6}.

物品的容积集W ＝{54，183，106，82，30，58，71，166，117，190，90，191，205，128，110，89，63，6，140，86，30，91，156，31，70，199，142，98，178，16，140，31，24，197，101，73，169，73，92，159，71，102，144，151，27，131，209，164，177，177，129，146，17，53，164，146，43，170，180，171，130，183，5，113，207，57，13，163，20，63，12，24，9，42，6，109，170，108，46，69，43，175，81，5，34，146，148，114，160，174，156，82，47，126，102，83，58，34，21，14}，背包的最大容量 6 718，规模为d＝100.

3)KP问题实例3(150个物品)

该实例是用实例 1和实例 2的数据构造出 150个物体的背包问题.

物品的价值集C ＝{597，596，593，586，581，568，567，560，549，548，547，529，529，527，520，491，482，478，475，475，466，462，459，458，454，451，449，443，442，421，410，409，395，394，390，377，375，366，361，347，334，322，315，313，311，309，296，295，294，289，285，279，277，276，272，248，246，245，238，237，232，231，230，225，192，184，183，176，174，171，169，165，165，154，153，150，149，147，143，140，138，134，132，127，124，123，114，111，104，89，74，63，62，58，55，48，27，22，12，6，220，208，198，192，180，180，165，162，160，158，155，130，125，122，120，118，115，110，105，101，100，100，98，96，95，90，88，82，80，77，75，73，72，70，69，66，65，63，60，58，56，50，30，20，15，10，8，5，3，1}.

物品的容积集W ＝{54，183，106，82，30，58，71，166，117，190，90，191，205，128，110，89，63，6，140，86，30，91，156，31，70，199，142，98，178，16，140，31，24，197，101，73，169，73，92，159，71，102，144，151，27，131，209，164，177，177，129，146，17，53，164，146，43，170，180，171，130，183，5，113，207，57，13，163，20，63，12，24，9，42，6，109，170，108，46，69，43，175，81，5，34，146，148，114，160，174，156，82，47，126，102，83，58，34，21，14，80，82，85，70，72，70，66，50，55，25，50，55，40，48，50，32，22，60，30，32，40，38，35，32，25，28，30，22，25，30，45，30，60，50，20，65，20，25，30，10，20，25，15，10，10，10，4，4，2，1}，背包的最大容量7,718，规模为d＝150.

对上述3个实例进行迭代计算，AGGA算法及其他算法的计算结果如表1所示.

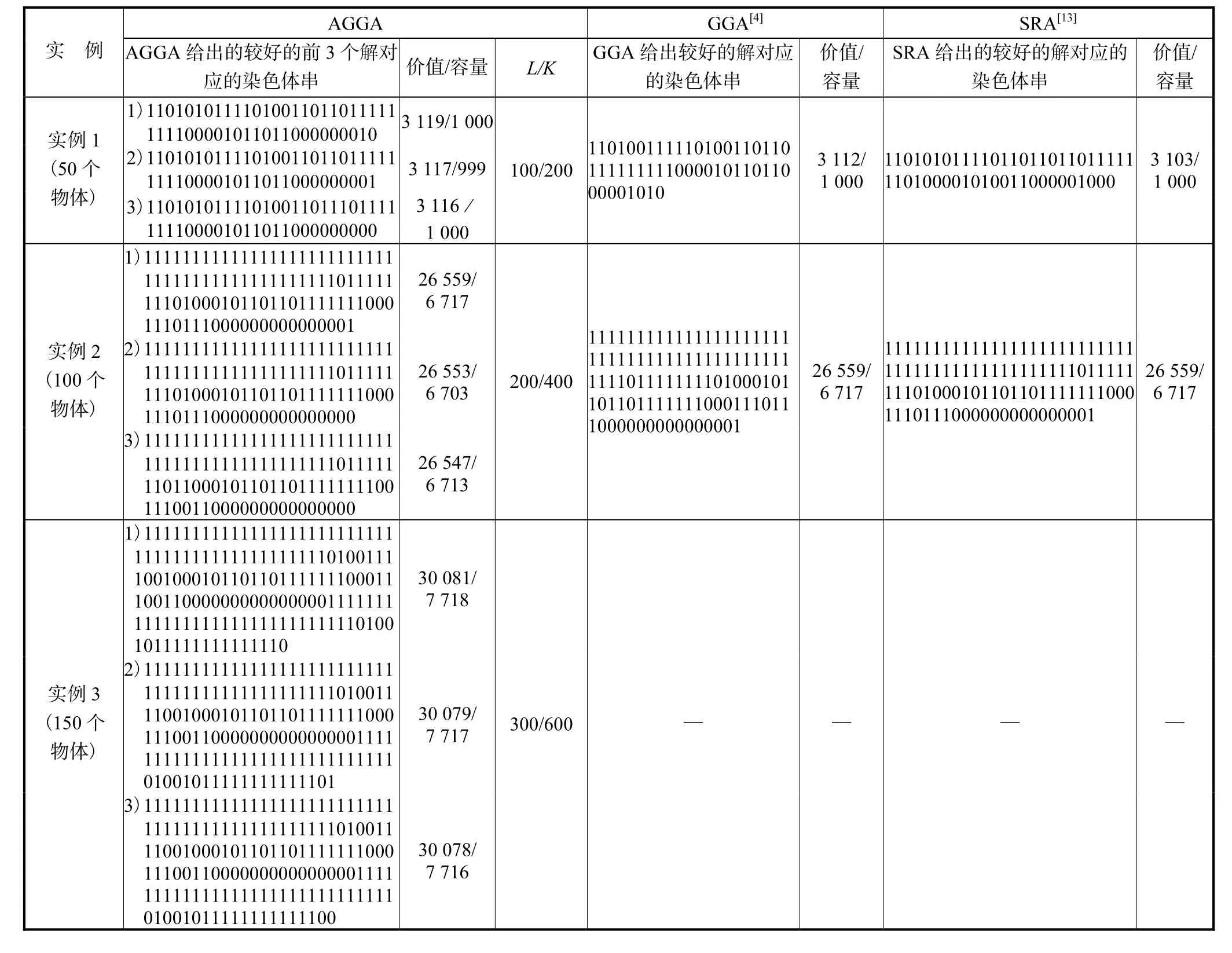
表1 3种算法计算结果的比较Tab.1 Comparisons of computing results of three algorithms

表1列出了AGGA、GGA、SRA对实例1、实例2的计算结果比较.从表1中可以看出：对于实例1，本文给出的计算结果 3,119/1,000比文献[4]中的 GGA算法和文献[13]中的 SRA算法求得的结果更优.对于实例3，运用本文提出的AGGA算法的最优计算结果为 30,081/7,718，将本例 3在专业线性规划软件Lingo9.0上面进行计算，计算结果为 30,085/7,718，本文结果与最优解差为 0.1%.用遗传算法最优距[14]概念来看本文结果“优”的程度，其最优距为 4 ×2-150，是相当满意的解.遗传算法与其他算法相比，构造简单，由于是并行计算，可以同时得到一批好的解，限于篇幅，在表1中只列出了每个问题的前3个解.

3 结 语

本文中提出的基因属性保留遗传算法AGGA，在计算背包问题时很好地解决了提前收敛和 GA欺骗问题，从很少的群体出发，就可以达到好的结果.本文中给出了背包问题规模与初始群体、进化代数的确定关系，即设背包的物体数量为n，可取初始群体为2n，进化次数为4n，这是非常高效的遗传算法计算参数.本文研究方法对其他类似问题有很好的借鉴意义.

［1］宁爱兵，马 良. 0/1背包问题快速降价法及其应用[J].系统工程理论方法应用，2005，14(4)：373-374.

Ning Aibing，Ma Liang. A quick reduction algorithm and its applications for 0/1-knapsack problem [J].Systems Engineering Theory Methodology Application，2005，14(4)：373-374(in Chinese).

［2］李鸣山，郑海虹. 0-1背包问题的多重分支-限界算法[J]. 武汉测绘科技大学学报，1995，20(1)：84-85.

Li Mingshan，Zheng Haihong. A multi-branch-and-bound algorithm for 0-1 knapsack problems [J].Journal of Wuhan Technical University of Surveying and Mapping，1995，20(1)：84-85(in Chinese).

［3］王粉兰，孙小玲. 不可分离凸背包问题的拉格朗日分解和区域分割方法[J]. 运筹学学报，2004，8(4)：46-47.

Wang Fenlan，Sun Xiaoling. A Lagrangian decomposition and domain cut algorithm for nonseparable convex knapsack problems [J].OR Transactions，2004，8(4)：46-47(in Chinese).

［4］贺毅朝，刘坤起，张翠军，等. 求解背包问题的贪心遗传算法及其应用[J]. 计算机工程与设计，2007，28(11)：2656-2657.

He Yichao，Liu Kunqi，Zhang Cuijun，et al. Greedy genetic algorithm for solving knapsack problems and its applications [J].Computer Engineering and Design，2007，28(11)：2656-2657(in Chinese).

［5］张 铃，张 钹. 佳点集遗传算法[J]. 计算机学报，2001，24(9)：918-921.

Zhang Ling，Zhang Bo. Good point set based genetic algorithm [J].Chinese Journal of Computers，2001，24(9)：918-921(in Chinese).

［6］史 亮，董槐林，龙 飞，等. 求解大规模 0-1背包问题的主动进化遗传算法[J]. 计算机工程，2007，33(13)：31-33.

Shi Liang，Dong Huailin，Long Fei，et al. Genetic algorithm based on active evolution for large scale 0-1 knapsack problem[J].Computer Engineering，2007，33(13)：31-33(in Chinese).

［7］李敏强，寇纪淞，林 丹，等.遗传算法的基本理论与应用[M]. 北京：科学出版社，2002.

Li Minqiang，Kou Jisong，Lin Dan，et al.The Basic Theory of Genetic Algorithm and Application[M]. Beijing：Science Press，2002(in Chinese).

［8］刘西奎，李 艳，许 进. 背包问题的遗传算法求解[J]. 华中科技大学学报，2002，30(6)：90.

Liu Xikui，Li Yan，Xu Jin. Solve knapsack problem by semi-feasible genetic algorithm[J].Journal of HuazhongUniversity of Science and Technology，2002，30(6)：90(in Chinese).

［9］宋海洲，魏旭真. 求解 0-1背包问题的混合遗传算法[J]. 华侨大学学报：自然科学版，2006，27(1)：16-19.

Song Haizhou，Wei Xuzhen. A hybrid genetic algorithm for solving 0-1 knapsack problem[J].Journal of Huaqiao University：Natural Science，2006，27(1)：16-19(in Chinese).

［10］李庆华，潘 军，李肯立. 背包问题的二分网格算法[J]. 计算机科学，2005，32(6)：217-220.

Li Qinghua，Pan Jun，Li Kenli. A dimidiate grid algorithm for the unbounded knapsack problem[J].Computer Science，2005，32(6)：217-220(in Chinese).

［11］霍红卫，许 进，保 铮. 基于遗传算法的 0/1背包问题求解[J]. 西安电子科技大学学报，1999，26(4)：494-496.

Huo Hongwei，Xu Jin，Bao Zheng. Solving 0/1 knapsack problem by using genetic algorithm[J].Journal of Xidian University，1999，26(4)：494-496(in Chinese).

［12］曾 智，杨小帆，陈 静，等. 求解多维 0-1背包问题的一种改进的遗传算法[J]. 计算机科学，2006，33(7)：220-221.

Zeng Zhi，Yang Xiaofan，Chen Jing，et al. An improved genetic algorithm for the multidimensional 0-1 knapsack problem[J].Computer Science，2006，33(7)：220-221(in Chinese).

［13］Li Kangshun，Jia Yuzhen，Zhang Wensheng，et al. A new method for solving 0/1 Knapsack problem based on evolutionary algorithm with schema replaced [C]//Proceedings of the IEEE International Conference on Automation and Logistics. Qingdao，China，2008：2569-2571.

［14］马丰宁，寇纪淞. 遗传算法中满意度与最优距[J]. 系统工程理论与实践，1998，18(1)：18-21.

Ma Fengning，Kou Jisong. The “satisfactory degree” and“optimum radius” in genetic algorithms theory [J].Systems Engineering Theory and Practice，1998，18(1)：18-21(in Chinese).

Attribute Gene-Reserved Genetic Algorithm for Solving Knapsack Problem

MA Feng-ning，XIE Long，ZHENG Zhong
(School of Management，Tianjin University，Tianjin 300072，China)

The genetic algorithm is an effective means to solve the large-scale knapsack problem. By studying several effective genetic algorithms，we find that the evolutional algebra of genetic algorithm has much more impact on optimal results than population size does. In addition，maintaining the effectiveness of gene-bit data also has a significant impact on the efficiency of evolution. In this paper，we propose the attribute gene-reserved genetic algorithm(AGGA)，which，combined with the genetic algorithm of elitist strategy，can reserve the difference of each genebit data attribute in genetics of different generations，and easily solve the early convergence and GA deceptive problem. Just from a very small number of groups，we can finally achieve good results，justify the high efficiency of improved algorithm and gain a calculation result better than the ones in relevant references. Then we construct a calculation example which contains 150 backpacks.

genetic algorithm；simple colony；attribute gene-reserved；elite reservation strategy；knapsack problem

TP301.6

A

0493-2137(2010)11-1020-05

2009-04-01；

2009-07-19.

国家自然科学基金资助项目（70571057）.

马丰宁（1958— ），男，博士，副教授.

马丰宁，fnmmm@vip.sina.com.