一种有效的SVM参数优化选择方法

赵璐华，彭 涛

ZHAO Lu-hua1,2, PENG Tao1

（1. 河南质量工程职业学院，平顶山 467000；2. 华中科技大学 计算机学院，武汉 430011）

一种有效的SVM参数优化选择方法

An effective SVM parameter selection optimazation method

赵璐华1,2，彭 涛1

ZHAO Lu-hua1,2, PENG Tao1

（1. 河南质量工程职业学院，平顶山 467000；2. 华中科技大学 计算机学院，武汉 430011）

支持向量机（SVM)在机器学习中的有着广泛应用，参数优化则是SVM需要解决的重要问题。本文提出了使用多主体进化算法(multi-agent genetic algorithm, MAGA)，通过设计自学习、协作、变异、竞争四个遗传算子，在参数空间进行搜索，实现SVM参数的优化选择.仿真算例表明该算法明显优于传统算法。

SVM；multi-agent；遗传算法；参数优化

0 引言

支持向量机(support vector machines, SVM)[1]是在统计学习理论的基础之上发展起来的新一代机器学习算法，它能较好的解决传统机器学习算法难以解决的小样本、高维、学习机器的结构、学习算法的局性收敛等问题，目前在复杂系统建模、预测、控制、时间序列分析、函数估计和模式识别等各个领域得到了广泛的应用。但是如何选择合适的参数则是支持向量机算法理论和应用中需要解决的主要问题，直接影响SVM的性能，对支持向量机的发展有重要的理论和实际意义。对于回归型支持向量机则首先需要确定三个自由参数[2]：不敏感值，正则化参数以及核参数，然后才能采用支持向量估计方法进行回归估计。

一般研究人员采用既直观又简单的试验确定参数来获得较优参数，这种方法需要大量的试验，而且通常得不到的最优参数。经典的“留一法”[2]（Leave-One-Out）采用的是方法是先根据人工选择近似最优值参数范围，然后在参数集合上进行穷举搜索得到最优参数，计算量相对较大，而且人工选择范围相对较难。Chapelle[3]提出用梯度下降法来完成SVM参数的自动选择，该方法在计算时间上有明显的改善，但是GD对初始点要求比较高，而且比较容易陷于局部最优解，而且初值选择不当，则更难获得局部最优解。Keerthy[4]采用拟牛顿法进行Gaussian核函数SVM模型的参数优化。Leung[5]提出了基于实值遗传算法（genetic algorithm, GA）实现了SVM模型参数的自动选择，该方法基于遗传算法的隐含并行高效性和全局最优的性能选择了SVM模型参数，提高了SVM的构造效率，而且进一步提高了分类器的识别率。但是GA算法存在适应度函数的适应性是局部的，同时没有考虑到生物之间协同的可能性，还不具备后天的学习能力等局限性。邵信光[6]提出了基于粒子群算法的SVM参数优化方法，该方法是通过个体之间的协作来寻找最优值的，其主要优点是较易实现。

多主体进化算法[7,8](multi-agent genetic algorithm, MAGA)是从智能体的角度出发，把进化算法中的个体作为一个具有局部感知、竞争协作和自学习能的智能体，通过智能体与环境以及智能体间的相互作用达到全局优化的目的。这种方法在搜索空间较大时，由于考虑到进化过程中个体的协作性及学习能力，搜索效率远远高于传统的遗传算法。该方法已经应用于函数优化，多目标优化，组合优化等理论问题，并解决了时延受限组播，VLSI布局等实际问题。

本文提出了基于智能体遗传算法的回归型支持向量机参数优化方法，利用多主体进行计算快速全局的搜索能力实现模型的优化选择，并采用两个常见的函数算例进行算法测试，表明该算法的优越性。

1 支持向量机的基本算法描述

其中L(.)表示损失函数。通过核函数把非线性数据映射到高维空间，在高维空间进行线性回归。二次规划优化形式可以转化为：

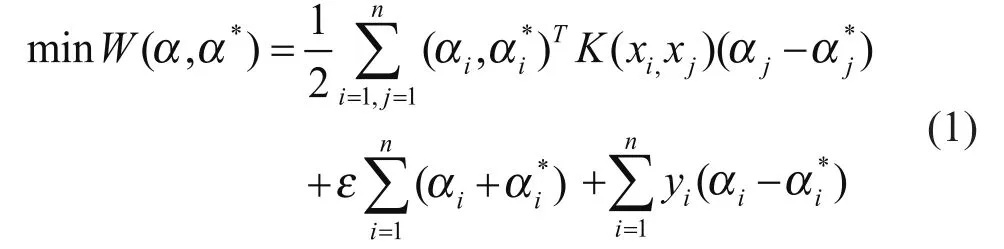
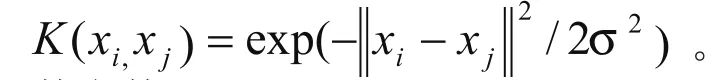
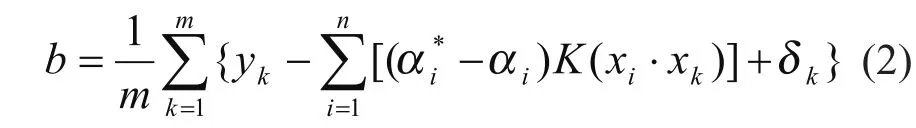
由此可以知道，在回归型支持型向量机中，正则化参数c，以及核参数σ均是需要选择的，为了SVM具有良好应用能力，有必要使用优化算法对该上述参数进行调整。

2 基于智能体遗传算法的回归型 SVM参数优化

SVM的参数优化实质是一个目标优化问题，首先确定SVM参数优化的性能评价指标，然后在搜索空间进行搜索，求解出最优参数。多主体进化是一种基于协同组织进化原理的优化算法，其在超高维函数优化、多目标优化及分解函数优化上有巨大潜力，并证明有较强的收敛性[8]。故本文采用多主体进化算法来实现SVM的参数优化。

2.1 回归型SVM参数优化性能指标

对于回归型参数优化性能指标是参数优化的基础，一般采用推广能力估计的方法。常用的方法有留一法、k-fold交叉验证法、支持向量率法、VC维方法。由于留一法的简洁实用性，一般采用该方法进行误差检验。

留一过程中首先得确定其误差数的上界，由半径-间隔界反映，表示为[10]

至此，可由标准SVM算法求得其α和β值，故Gaussian核函数SVM的问题是优化正则化参数c和核函数参数σ，使得W最大而T最小。

2.2 智能体遗传算法的原理

智能体遗传算法通过设计每个主体的目的，生存环境，局部环境定义，行为来设计用来优化的主体。将主体定义为待优化目标的一个候选解，记为，它的能量等于目标函数取反，即E(p)=-f(p)，其中Q表示变量个数。为了实现主体的局部感知能力，将生存环境组织成网格状结构，称为主体网格，记为G，相应的固定在网格点(i,j)不能移动的主体记为pi,j，所以主体均与其邻域的局部主体发生作用，具体为竞争与协作，通过扩散实现信息的全局共享，通过自学习与变异实现自身信息的更新。由自学习、竞争、协作与变异四种机制完成主体的进化，进行寻优。多主体进化算法的关键在于算子的设计。

主体拥有与所求解问题相关的知识，可以利用这些知识进行自学习来提高性能，在此用局部搜索来实现：

2.2.2 协作算子X(pi,pj)[12]

协作算子可能理解为主体之间的信息共享，在此先用邻域正交交叉算子[12]生成主体集合P，|P|=M。再用P中能量最高的主体作为协作算子的结果：

2.2.3 变异算子v(P)[13]

变异采用普通的标准正态分布随机数方法：

U(0,1)为(0,1)区间均匀分布的随机数，Pv为变异概率，Pv=(e1,e2,...,eQ)，且t为进化代数。

2.2.4 竞争算子r(P)[14]

与邻域主体的竞争只需要与邻域中能量最大者竞争，记其为Pmax，则竞争行为准则为：

其中Pnew为通过自学习、正交交叉和变异后产生的主体。

2.3 基于智能体遗传算法的支持向量机的参数调整

为了用智能体遗传算法优化SVM的参数，首先必须对参数进行编码，对正则化参数c和核参数 σ的编码用主体P=(C,σ)表示，定义Bestt和CBestt分别为前t代产生的最优主体和第t代产生的最优主体，ts为最大能量不变代数，即ts=max{τ|Bestt=Bestt+τ}，为了改善算法的收敛性能，设定以最大进化代数tmax与最大能量不变代数tsmax为双重进化终止准则。算法的流程如下：

1）令t=0，初始化主体网格G中的所有主体pi,j，由于没有先验信息，采用随机生成方案，即pi,j=rand(P)，P为解的编码空间，更新Bestt，Bestt+τ，ts ；

2）对第t代的每个主体pi,j分别用式3.4～3.7进行自学习、协作、变异和竞争，产生新一代主体，其中E(pi,j)由标准SVM算法求得；

3）更新Bestt，Bestt+τ，ts ；

3 仿真算例

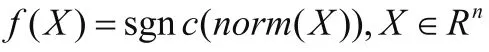
3.1 一维函数算例

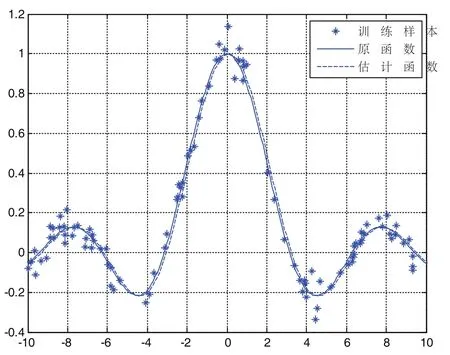
图1 一维函数SVM仿真算例

3.2 二维函数算例

图2 二维函数SVM仿真算例

3.3 试验结果分析

将上述算法与使用正交优选方法、遗传算法、以及基于PSO遗传算法的结果进行比较，一维函数算例实验结果比较如表1所示，二维函数仿真算例实验结果比较如表2所示，从表中可见，利用本文方法所得的SVM模型的支持向量个数最少，测试误差最小。

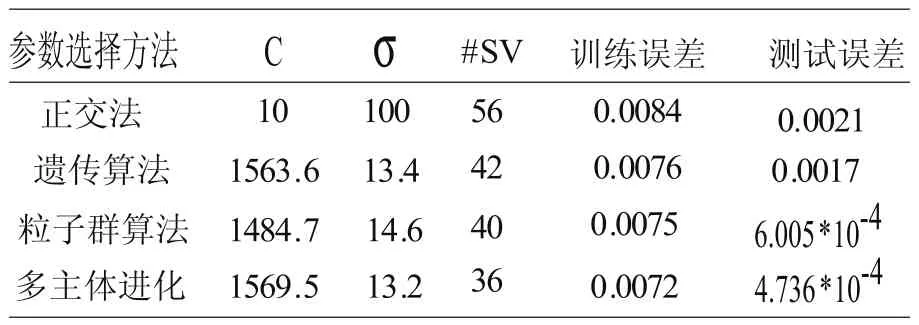
表1 一维函数仿真算例结果对比表

表2 二维函数仿真算例结果对比表

4 结论

本文提出了基于智能体遗传算法的支持向量机参数估计方法，通过设计自学习算子、协同算子，避免了传统进化算法中只考虑基因的竞争因素而未考虑到基因的协同，加快了收敛速度，提高了变异的有效性，实现了支持向量机的参数优选。

[1] Marti Hearst.Support Vector Machines[J].IEEE Transaction On Intelligent Systems,July/August,1998.

[2] Lee J H,Lin C J.Automatic Model Selection for Support Vector Machines[R].Taipei：Taiwan University,2000.

[3] Chapelle O,Vapnik V,Bousquet O,et al.Choosing Multiple Parameters for Support Vector Machines[J].Machine Learning,2002,46(1-3)：131-159.

[4] ZHENG Chunhong,JIAO Licheng.Automatic parameters Selection of SVM based on GA[C].Proc of the 5th World Congress on Intelligent Control and Automation.Piscataway, NJ：IEEE press,2004：2035-2040.

[5] Leung Y W,Wang Y.An orthogonal genetic algorithm with quantization for global numerical optimization[J].IEEE Trans Evolutionary Computation.2001,5(1)：41-53.

[6] 邵信光,杨慧中,陈刚.基于粒子群算法的支持向量机参数优化及其应用[J].控制理论与应用.2005,5(23)：740-743.

[7] Zhong Weicai,Liu Jing,Xue Mingzhi,etal.A muti-agent genetical-algorithm for global numerical optimization[J].IEEE Transactions on Systems,Man,and Cybernetics partB：Cybernetics,2004,34(2).

[8] 钟伟才,刘静,焦李成.多智能体遗传算法用于线性系统逼近[J].自动化学报,2004,30(6)：933-938.

[9] F.E.H.Tay,L.-J Cao,Application of support vector machines in financial forecasting[J].Omega.2001,4(9)：309-317.

[10]F. Friedrichs and C.Igel. Evolutionary tuning of multiple SVM parameters[J].Neurocomputing, 64：107 -117,2005.

[11]C.Gagne,M.Schoenauer,M.Sebag,and M.Tomassini.Genetic programming for kernel based learning with co-evolving subsets selection[C].In Proceedings of Parallel Problem Solving in Nature,2006.

[12]T. Phienthrakul and B.Kijsirikul.Evolutionary strategies for multi-scale radial basis function kernels in support vector machines[C].In Proceedings of the Genetic and Evolutionary Computation Conference,pages 905-911,Washington,DC, June 2005.ACM Press.

[13]C.-L.Huang and C.-J.Wang.A GA-based feature selection and parameter optimization for support vector machines.[J]Expert Systems with Applications,31：231-240, 2006.

[14]Smeaton,A.F.,Over,P.,and Kraaij,W.2006. Evaluation campaigns and TRECVid[C].In Proceedings of the 8th ACM International Workshop on Multimedia Information Retrieval(MIR 2006),Santa Barbara,California,USA,October 26-27,2006.

TP391.9

A

1009-0134(2010)09-0146-04

10.3969/j.issn.1009-0134.2010.09.45

2009-11-11

赵璐华（1972 -）,女，河南平顶山人，副教授，研究方向为计算机应用技术。