量子粒子群算法在面向再制造的flow-shop问题中的应用
2010-04-11胡金涛叶春明
胡金涛,叶春明,叶 林
HU Jin-tao, YE Chun-ming, YE Lin
(上海理工大学 管理学院,上海 200093)
量子粒子群算法在面向再制造的flow-shop问题中的应用
Application of quantum particle swarm optimization algorithm in flow shop scheduling based on remanufacturing
胡金涛,叶春明,叶 林
HU Jin-tao, YE Chun-ming, YE Lin
(上海理工大学 管理学院,上海 200093)
对再制造的各环节进行分析,研究出再制造生产阶段的目标——流水线生产。针对 粒子群优化算法搜索空间有限、容易出现早熟现象的缺陷,采用量子粒子群算法设计单一生产商再制造系统流水线生产的机制,通过随机初始种群,修正非法解,量子旋转门更新,运用MATLAB编程仿真测试得到大规模生产的优化结果,取得较好结果。
再制造;量子粒子群;修正非法解;flow-shop
0 引言
再制造概念的提出打破了传统的“从摇篮到坟墓”的单生命周期,实现了废旧产品新生的过程。再制造(Remanufacturing)是指通过回收、拆卸、分拣、清洗、喷涂、翻修、及再装配等环节,修复或改造废旧产品,恢复零部件或产品性能的技术和活动[1],是实现绿色循环经济的有效途径。目前,欧美等国汽车零部件再制造利用基本上达到80%以上,并已在技术、加工、销售等方面形成一套完整体系,而国内产品还主要集中在发动机、变速器、电机等附加值较高的汽车零部件上,对于其他零部件无论从技术、资金还是设备上,还无暇顾及。因此,再制造工业是未来中国制造业的必经之路。
量子计算(quantum computation, QC)的研究开始于1982年,现已经成为世界各国紧密跟踪的前沿研究领域之一。相对于经典算法而言,其最本质的特征就是利用了量子态的叠加性和相干性,以及量子比特之间的纠缠性,由此,研究者们依据量子比特的特性提出了量子进化算法(QEA)。虽然理论上已经证明QEAZ在寻优过程中要比一般算法好,然而,QEA本身存在着缺陷,在操作和更新量子比特过程中,设定的参数比较多,操作繁琐,容易早熟,特别是没有利用其他未成熟个体携带的全局最优值信息。因此,一些学者将量子计算中的一些基本概念引进到经典计算中,从根本上改善算法的性能。例如:Han[2]将量子概念和遗传算法相结合,在解决经典的组合优化问题上,显示出很好的性能。Sun[3]提出了基于量子行为的微粒群算法(PSO),将微粒群算法的寻优理念纳入QEA,保留了PSO中的极值跟踪及邻域搜索,加速算法的收敛,Sun的算法本质是模拟薛定谔方程,是封闭量子系统演化的一种方式,表现出了非常好的性能。
本文提出的量子粒子群算法利用量子比特进行编码,通过量子旋转门进行粒子更新,保留了粒子群算法的进化方程,加入了全干扰交叉拓宽搜索的范围,引入了变量搜索加强局部搜索能力,加速算法的收敛。
1 量子进化算法和粒子群算法
1.1 量子进化算法
量子进化算法(QEA)是在概率进化算法的基础上发展起来的新的进化算法。它采用量子比特染色体编码,通过量子门变异来进化染色体,然后观察量子染色体的状态来生成二进制解,最后通过量子旋转门实现进化操作。
在量子进化算法中,最小的信息单元为1量子比特。1量子比特的状态可以取值0或者1,或者任一叠加态,表示如下:
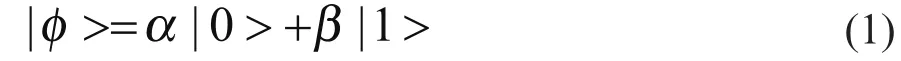
因此,粒子的量子表示方法可以通过使用概率幅或相位加以表示。如第t代的种群为Q(t)={q1t,q2t,...,qnt},qnt即为染色体,具体形式可以描述如下:
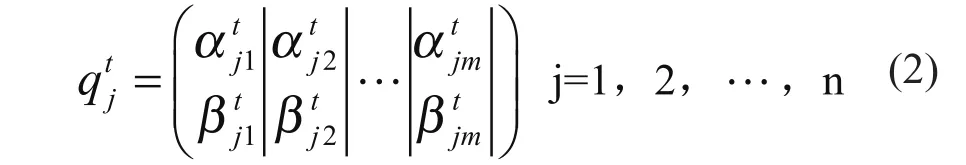
QEA的一般步骤如下:
1)初始化种群Q(t),t=0;
2)由Q(t)生成二进制序列P(t);
3)评价P(t)的适应度,并保存最优解;
4)停止条件判断:如果满足停机条件,则输出当前最优个体,算法结束,否则算法继续;
5)更新Q(t),t=t+1,返回2)。
算法中,Q(t)表示量子染色体的种群,P(t)表示二进制染色体种群,在第t代中,Q(t)={q1t,q2t,...,qnt},P(t)= {X1t,X2t,...,Xnt}(n表示种群大小),每个二进制解 Xjt(j=1,2,...,n)是长度为m的二进制串,它是由量子比特幅|αit|2或者|βit|2得到的,对应二进制情况的过程是随机产生一个[0,1]数,若它大于|αit|2,取1,否则取0。在第5)步更新Q(t)中,采用量子旋转门对Q(t)进行更新,量子门的设计有多种形式,如非门、受控非门、Hadamard门等,最常用的量子旋转门如下:
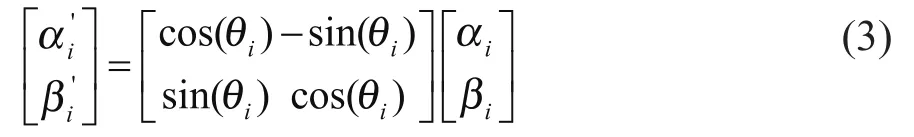
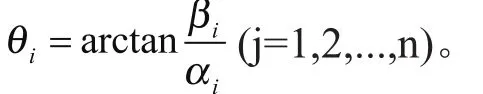
1.2 粒子群算法(PSO)
PSO最早是由Kennedy和Eberhart于1995年提出的[4]。受到人工生命(Artificial Life)的研究结果启发,PSO的基本概念源于对鸟群捕食行为的研究。PSO算法首先初始化一群随机粒子,然后通过进化(迭代)来找到最优解。在粒子的每一次进化中,通过跟踪两个极值来更新自己,一个极值是粒子本身所能找到的最优解,即个体极值pbest,另一个是整个群体目前找到的最优解,即全局极值gbest。粒子找到这两个极值后,就根据下面两个公式更新自己的速度和位置:

其中,d表示粒子的维度,i表示第i个粒子(j=1,2,...,n),t表示迭代的次数, Xit(Xi1t,Xi2t,...,Xidt)表示t时刻d维搜索空间中的第i个粒子的位置,Vit(vi1t,vi2t,...,vidt)表示t时刻d维搜索空间中的第i个微粒的速度,ω表示惯性权因子,c1,c2为正的加速常数,rand()为在0到1之间均匀分布的随机数[5]。
1.3 量子微粒群优化算法(QPSO)
为了改善微粒群算法的缺点,我们在原有的算法基础上引入了量子计算,形成量子微粒群算法,使得算法具有强大的领域搜索能力以及极值跟踪能力,能够改善微粒群算法后期搜索能力。
借鉴微粒群算法的速度更新公式,QPSO算法粒子的更新方式是:
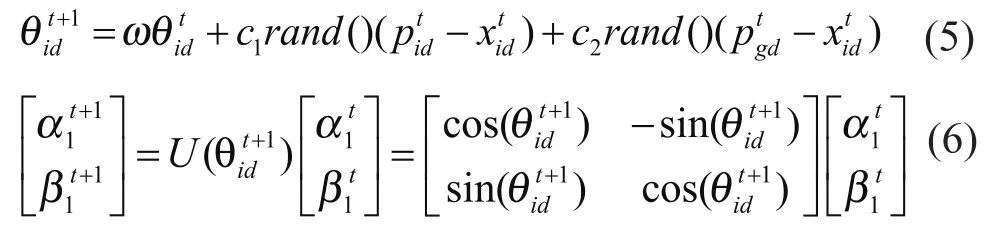
其中pid,pgd,c1,c2,xid的定义与PSO中的定义相同。
2 面向再制造的流水车间调度问题(FSP)的QPSO算法
2.1 再制造描述
在过去的十几年时间里,越来越多的人关注产品的回收,一方面绿色循环经济的出现为国家的发展提供了道理,一方面制造企业间竞争的加剧促使领导人员想方设法所见成本提高质量,再制造对于企业的长远发展举足轻重,为企业带来了额外利润。如今,发达国家工业领域销售的设备60%是再制造生产出来的。卡特彼勒上海再制造中心市场总监肖绍成曾向《中国投资》解释了再制造的生产流程:旧件从消费者手中收上来后,被全部拆解到最后一颗螺钉,进行清洗;然后,进行筛选,其中易损件需要100%更换,一部分是可以恢复到原状的,比如气缸盖,还有一部分是不需要修复的,比如螺钉,它只要清洗后就可以再次使用。把这三个部分:经过修复的、经过更换的和不需要修复的,重新组合成新的部件,这个过程就是再制造,如图1所示。
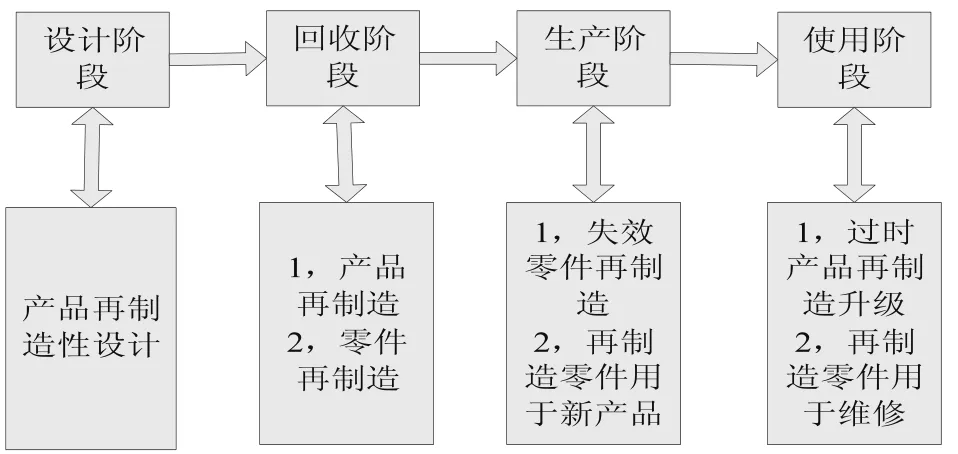
再制造流程[6]
图1为再制造的流程图,从回收阶段到使用阶段企业需要对回收产品做多方面处理,其技术难点就是寿命评估和修复,这就对企业的再制造能力形成了考验,虽然再制造为制造业的生产趋势,不过再制造本身具有很大的不确定性,主要表现在产品的回收质量,检测拆卸及再制造可靠性,对于生产调度提出了很高的要求。在生产阶段,我们不讨论回收产品质量,拆卸,可靠性及成本的不确定性,由于回收的产品再制造企业在设计阶段将其分门别类,对于一般通用件,企业再制造生产过程仍然是基于flow-shop的调度。
2.2 fl ow-shop描述[7]
Flow-shop调度问题是一种典型的组合优化问题,一般可以描述为:n个工件在m台机器上加工,一个工件分为k道工序,每道工序要求不同的机器加工。n个工件在m台机器上的加工顺序相同,工件i在机器j上的加工时间是给定的,设为tij(i=1,2,…,n;j=1,2,…,m)。调度问题的目标函数是求n个工件的最优加工顺序,使最大流程时间最小。
对流水车间调度问题常作如下假设:
1)每个工件在机器上的加工顺序相同,且是确定的;
2)每台机器在每个时刻只能加工某个工件的某道工序;
3)一个工件不能同时在不同机器上加工;
4)工序的准备时间与顺序无关,且包含在加工时间中。
车间调度问题的完工时间可以表示为:
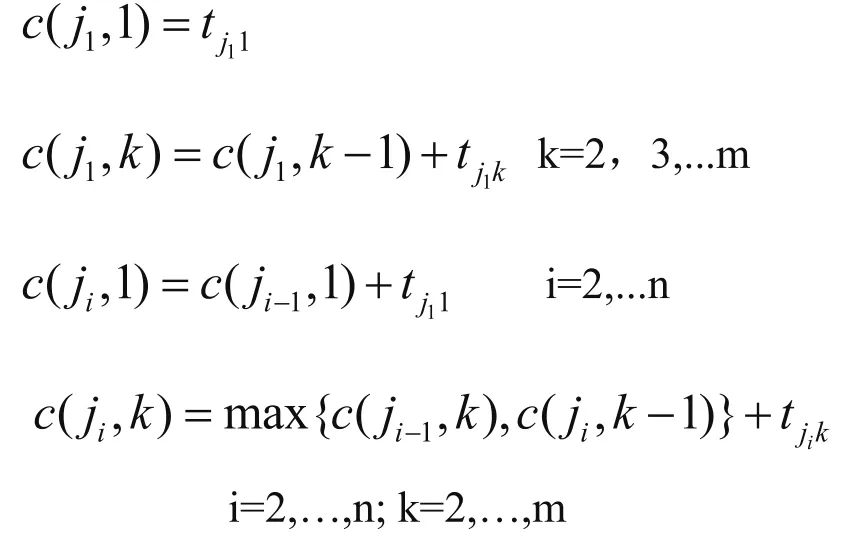
最大流程时间为cmax=c(jn,m)
2.3 粒子编码方式
本文采用二进制的基于工件的编码方式,对于n个工件,m台机器的flow-shop问题,每个粒子对应n维向量,每个向量用ceil(log2(n))位二进制染色体编码表示,即每个粒子用ceil(log2(n))*n位二进制量子染色体表示,量子染色体由量子比特坍缩而成。
例如工件数为3,若某粒子的染色体表示如下:

将粒子二进制编码解码为十进制数:

按元素值大小顺序对x重新整数序规范:

则该粒子x的调度顺序为:j3-j1-j2
2.4 修正非法解
将量子坍塌得到的每组二进制串xjt都转化为n个十进制工件编号,此时每个个体都变成了n个十进制数,因此整个种群可以得到N(N 为维数)个解,也就是N中调度安排,但是由于初始化时,编码是通过随机产生的,所以必然存在不可行的工件编号,因此需要对不可行编码进行修复:
1)通过ceil(log2(n))得到x的范围,将工件号对应的x从编码范围内除去;
2)判断编码中的工件号对应的x是否重复,若重复,则找出相同的数,在剩余的编码范围内随机选择一个数,以进行工件排序,保证每行的工件对应的x值都不相同,且均在编码范围内。
QPSO流程步骤:
1)初始化参数;
2)令t=0,初始化Q(t);
3)由Q(t)观测得到P(t);
4)由P(t)生成序列Y(t);
5)由于生成的十进制整数Y(t),因此对该十进制序列进行修正非法解,使之成为每行的数值都不相等。
6)在修正非法解后,对该十进制序列进行二进制转化,再通过一定机制将其转化为概率幅矩阵,以便得到更新后的相位阵;
7)采用上文提到的编码方式将十进制序列转换成工件的排列,本文的维度为10,因此将得到10个工件的排列X(t)。
8)评价X(t)的适应度(加工时间);
9)标记本代粒子最优的相位为pbest,并标记粒子全局最优的相位为gbest;
10)t=t+1,采用量子旋转门更新种群;
11)更新pbest和gbest;
12)如果满足算法终止条件,停止,否则转3)。
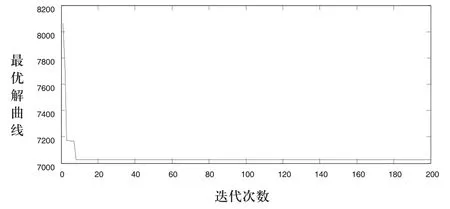
图2 迭代最佳适应值情况
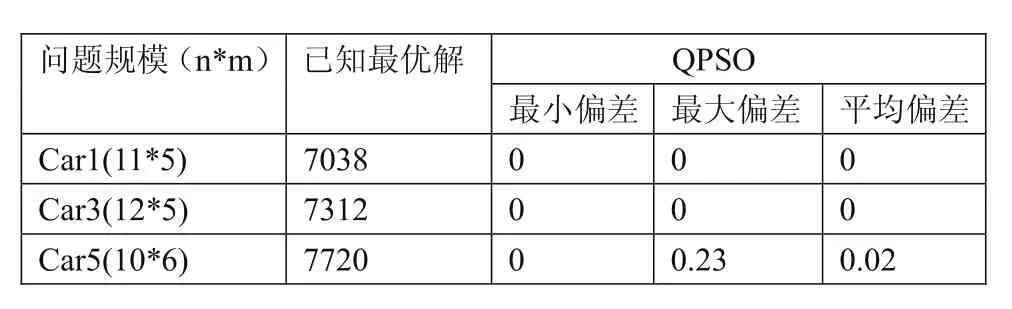
表1 Flow-Shop Benchmark问题求解结果
本文对表1中的三种问题规模进行随机20次运行,最小偏差指的是算法运行20次找到的最小时间,与已知最优解之间的相对误差;平均偏差指的是20次计算得到的最小时间的平均值与已知最优解之间的相对误差。
图2采用了QPSO对Car1(11*5)优化的结果,参数设置如下:种群规模为10,最大迭代次数为200,C1和我C2为2,采用动态权重法,从曲线的收敛情况来看,算法在第7代求得最优解,收敛速度快,很好把握了多样化搜索的分散性和保证种群质量的收敛性之间的平衡。
3 结束语
本文是量子粒子群算法的面向再制造的flowshop调度,对于再制造下的flow-shop问题设计较为理想,仅仅考虑再制造企业生产阶段的生产方式,相对生产阶段,设计阶段技术要求比较高,多一些有效的管理方法,就会少一些纰漏,本文运用MATLAB编程测试改进的量子粒子群算法求解flop-shop问题,取得较好的结果。
[1] 徐滨士.汽车发动机再制造效益分析及对循环经济的贡献[J].中国表面工程,2005(1):1-7.
[2] Han K,Kim JH.Genetic quantum algorithm and its application to combinatorial optimization problems[C]//Proceedings of the 2000 IEEE Conference on Evolutionary Computation,Piscataway,IEEE Press,2000:1354-1360.
[3] Sun J,Feng B,Xu WB.Particle swarm optimization with particles having quantum behavior[c]//Proceedings of IEEE Conference on Evolutionary Computation,2004:326-331.
[4] Kennedy J,Eberhart R.Particle Swarm Optimization[C].In:IEEE International Conference on Neural Networks, Perth,Australia,1995:1942-1948.
[5] 王凌,刘波.微粒群优化与调度算法[M].北京:清华大学出版社,2008.
[6] 崔培枝,姚巨坤,许艺.面向再制造全过程的管理.新技术新工艺·机械加工与自动化,2004,7.
[7] 王万良,吴启迪.生产调度智能算法及其应用[M].北京:科学出版社,2007.
TH166
A
1009-0134(2010)09-0064-04
10.3969/j.issn.1009-0134.2010.09.19
2009-10-26
上海市本科生创新基金(SH081025227)
胡金涛(1985 -),男,硕士研究生,研究方向为工业工程。
