基于视觉感受的曲面建模优化研究
2010-04-11陈定方
肖 文,陈定方
XIAO Wen 1, CHEN Ding-Fang2
(1. 武汉理工大学 艺术设计学院,武汉 430070;2. 武汉理工大学 智能制造与控制研究所,武汉 430063)
基于视觉感受的曲面建模优化研究
The optimization research of surface modeling based on the visual perception
肖 文1,陈定方2
XIAO Wen1, CHEN Ding-Fang2
(1. 武汉理工大学 艺术设计学院,武汉 430070;2. 武汉理工大学 智能制造与控制研究所,武汉 430063)
虚拟现实技术的主要目标就是使虚拟现实系统中的虚拟物体给人以真实存在的感觉。以当前的计算机图形学的发展水平来说,只要计算时间足够,就可以生成非常精细的画面。但VR系统是实时系统,它不仅需要追求场景效果的真实感,还需要顾及硬件系统的反应速度。因此,在高质量图形的实时生成要求下,如何减少三维模型的复杂程度,同时保证三维场景视觉上的精度,已成为数字模型的创建工作中的研究重点。本文以人的视觉感受为基准对模型优化所需达到的精度进行研究,并根据不同应用情形提出一些优化方案,从源头上就控制面数,其效果要比后期用程序进行优化,不仅在优化程度上要高得多,而且在视觉效果上也更优越。
曲面;仿真;建模;视觉感受;模型优化
0 引言
前段时间,我们实验室与有关单位合作进行复杂装备训练模拟器的开发,十分重要的一部分工作就是对复杂装备进行数字模型的创建工作。有关单位对于模拟器的真实感有很高的要求很多,建模要求达到与真实的装备在视觉上高度一致,保证训练时的虚拟操作与实际操作装备感受完全一致。
整个工作分为两大部分进行——利用Solid works软件专长于机械设计的特点进行建模,利用3D Max软件优秀的表现能力设定材质、设置动画。这样安排工作思路清晰,亦充分了利用各软件的特点。
在用Solidworks软件建模工作部分完成后,我们发现出现了一个很大的问题:输出到3D Max中的模型面数非常巨大,据不完全统计约有二千万个面之多。这是一个非常大的数据量,导致后面的工作几乎不能继续进行下去。
1 问题产生的原因
为了找到问题出现的原因,我们对整个模型进行了仔细分析、研究。初步发现面数过多的部分主要在物体倒圆角处和曲面的部分。
为了更准确地分析原因,从而找到优化的方法,我们做了一系列试验:首先在Solidworks中创建立方体、球体、八棱柱和圆柱各一个(图1),然后,将其转换成3D Max文件,在3D Max中分别查看各个物体的面数,结果转换后立方体有12个面,球体有22200个面,八棱柱有28个面,而圆柱则有556个面。

图1 创建的立方体、球体、八棱柱、圆柱
从上面几个物体面数来看,立方体和八棱柱等面数不产生变化,只是由于3D Max中统一采用三角形面描述物体,因此,物体实际的面数变多了;球体和圆柱体面数很多,通过仔细观察,发现主要是曲面表面被分割成很多细小的三角面造成的。这是在转换到3D Max的过程中,由于程序固有的原因,采用了很高的转换精度而产生的。我们试图通过调整转化参数也未能解决好这一问题。
从上面的试验可以看出,造成面数过多的原因主要在于造型中曲面或曲线的存在。
2 关于真实度视觉感受的讨论
真实感表现是计算机仿真发展的重要方向,在个人计算机性能不断提高的今天,追求对仿真对象更真实的表现成为自然而然的事。然而,无论计算机性能有多高,它的性能和资源毕竟是有限的,不可能满足我们对真实度的无限要求。因此,我们在开展建模工作以前必须确定一个合适的真实度的标准,而这一标准应该是以能够满足人眼的视觉感受为前提的。任何超过人眼能够感受到的精细程度都是多余和不必要的,是对人力资源、计算机资源和时间的浪费。
那么,什么是我们的眼睛能感受到的精细程度的极限呢?我觉得有两个条件限制了我们的视觉感受:显示装置的像素分辨率和人眼对色彩的分辨率。
首先,我们模型中的结构在光栅化的过程中,如果细小到小于一个像素的大小,可以想象得到它的任何形态已经毫无意义了,在屏幕上它仅仅是一个点而已。
其次,如果相邻两个面的色彩差别小于人眼对色彩的分辨率,则在我们的眼中就会视为同一颜色。因此,以下的讨论皆以此为依据进行。
在仿真中,物体的真实感主要体现在形体和质感(包括色彩、纹理、在光照下的反映等方面)的真实感两方面。本文主要讨论形体的真实感,它体现在两方面视觉感受的平滑度上:一是边缘的平滑度,二是表面的平滑度。
2.1 边缘平滑度的讨论
对于曲面物体形状的精度以往一直没有一个判断的标准,大多数都根据制作者的经验来调整,对于多数人来说不太好把握。
那么怎么确定这样一个标准呢?从前面我们知道显示装置的像素分辨率是曲面物体边缘平滑度的极限,由于曲面物体的曲线边缘是由一段一段的短小线段组成,首先从直觉就可以知道线段的长度不能小于两个像素,其次,我们假设用一个等边多边形来拟合一个圆,如果将这个等边多边形画在屏幕上与通过圆形方程直接在屏幕上画出的图形误差很小时,我们就可以认为这两个图形是等价的。
根据上面两条限制条件,我们以圆形为例分别进行推导,看看最少需要多少边形才能满足视觉上的光滑度。这里,假设一个半径为R像素的圆。
根据条件一,则有:
n>2*π*R/2 (n为多边形的边数,R为半径)
即n>π*R
根据条件二,则有(图2):
OA-OC<0.5 (OA与OC的差小于0.5像素,其中OA=R)
∴有R-R*cosθ<0.5 (其中θ=360°/2n,n为多边形的边数)
则n>180°/arccos((2R-1)/2R)
这表明在一定的半径条件下,只要多边形的边数达到n,在屏幕上看起来就是很光滑的圆了。
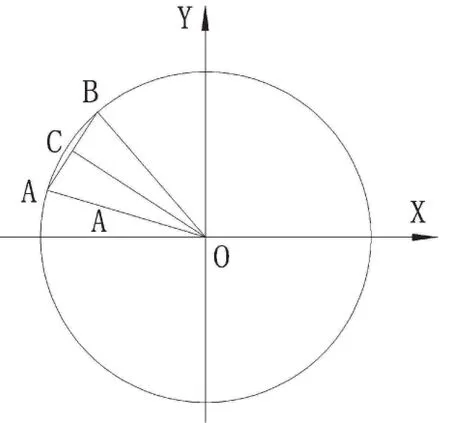
图2 等边多边形拟合圆的精度分析
最后,由两个条件取小值就可以确定多边形的最小边数。
2.2 表面平滑度的讨论
这里讨论的表面平滑度是指物体表面经渲染引擎渲染后在屏幕上显示效果的平滑程度。
在讨论前,我们先了解一下渲染引擎的基本工作方式。在各种渲染引擎中其核心都是以光照模型为基础的,因为至今视觉工业还是主要基于经验而不是物理定律,所以,Lambert、Blinn、Phong、Cook-Torrance、Strauss、Anisotropic等经验模型今天还可有生命力,而不至于被Radiosity和Raytrace等物理模型代替。Radiosity和Raytrace都有自己的光照定律,在各软件中还经常和以上经验模型混用,是因为他们还有很强的生命力。由于计算速度的限制,一般实时仿真引擎一般都使用上述经验模型。因为模型种类很多而且多数比较类似,在这里以最实用的Blinn-Phong模型为例[1]。
1975年Phong Bui Tong发明的Phong模型(图3),提出了计算镜面高光的经验模型,镜面反射光强与反射光线和视线的夹角α相关:
Ispecular = Ks*Is*(cos α) n
其中,Ks为物体表面的高光系数, Is为光强,α是反射光与视线的夹角,n为高光指数,n越大,则表面越光滑,反射光越集中,高光范围越小。
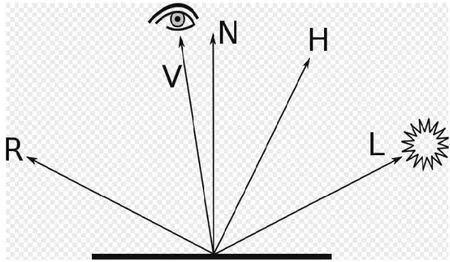
图3 Phong模型
Blinn-Phong模型也称Blinn模型,是Phong模型最常见的变化类型。作为CG领域的先驱,Blinn改进了Phong模型的一些高光上的问题。Blinn模型混合了Lambert的漫射部分和标准的高光,在速度上相当快,因此成为许多CG软件中的默认材质。此外它也集成在了大多数图形芯片中,用以产生实时快速的渲染。
对于各表面为平面的物体,渲染软件在对一个面进行光照效果计算的时候,首先确定该面的法线方向,带入光照模型中,就可以计算出每个像素的颜色值。
而对于曲面表面的物体,曲面被分解为一个个小的平面,在渲染的时候对相邻两个面之间的法线方向进行插值,便形成连续过渡的效果。这样,就可以用很少的面表现复杂的曲面。
我们可以做几个对比试验(图4),看看模型精度对于表面平滑效果的影响。
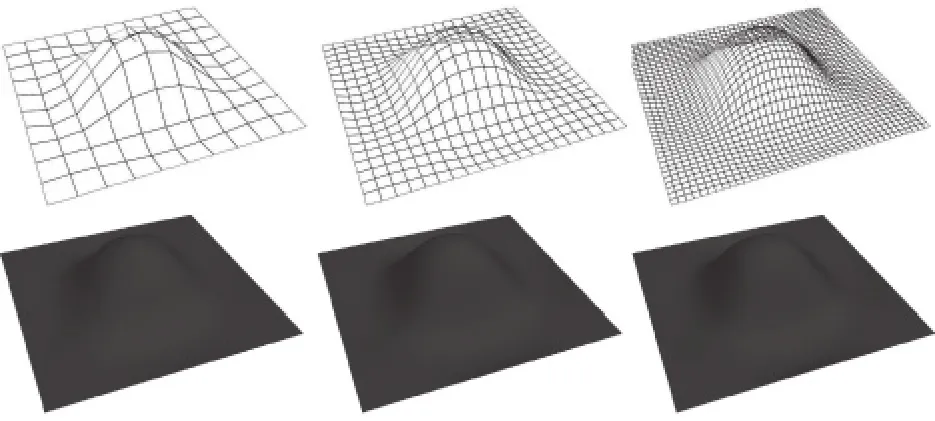
图4 几个对比试验(从左到右分别为10X10、20X20、40X40网格)
从图中可以看出由于运用了插值计算,模型精度对于表面平滑效果的影响不是太明显。
2.3 结论
从上面的讨论可以看出,从视觉感受方面来看,影响真实度的主要因素是边缘的平滑度,曲面的网格精度与边缘的精度是相关联的,由于人眼对曲面平滑度不及边缘平滑度敏感,因此,在考虑设定模型精度时以边缘的平滑度为标准确定就可以了。
3 优化方法
通过前面的讨论,可以知道要达到我们所需要的视觉真实感,很多时候并不需要很多的分段数,合理安排曲边的分段数才是曲面优化的关键。关于模型的优化已经有人做过了一些研究和探索,网上也有一些相关的文章和论文[2],也编写了一些优化模型的程序,比如Polygon Cruncher软件就是一个强大的模型减面工具,3D Max中也自带有一个优化工具,但通过实际运用,我们发现它们还是存在很多问题,如对于部分模型存在优化后物体外形产生了变形(图5),对于有的模型则基本不能优化。因此,在实际运用中,作者认为,需要从源头上就控制面数,其效果要比后期用程序进行优化,不仅在优化程度上要高得多,而且在视觉效果上也更优越。

图5 模型在优化后物体外形产生了变形(优化后圆倒角不见了)
在制作过程中,针对不同类型的物体可以采取两类优化方法:模型方法和纹理方法,下面分别进行阐述。
3.1 模型方法
这种方法主要针对较大的曲面,曲面中间很少开孔。在建模时首先根据曲面在屏幕上显示的尺寸(像素尺寸)按照前述的公式估算出边界的分段数,将曲面的边按需要的精度用折线绘制,相应的曲面则变为折面,在模型被转换到3D Max中后,选择组成曲面的各面,将其组成一个光滑组,这样在渲染输出的时候渲染程序就会对光滑组内的各个面进行插值运算,从而得到一个完美平滑的曲面了。其实,考虑到人眼对运动物体的分辨率会适当降低,在确定边界分段数的时候可以设为估算子的1/2甚至1/4,以进一步减少模型的面数。
3.2 贴图方法

图6 不透明贴图运用(从左到右分别为贴图、线框模型、贴图后的渲染效果)
对于一些次要的表面开有很多孔洞的物体,则可以采用一种更简洁的方法,即采用贴图的方法,可以用一张只具有黑白两色的图作为蒙板作用于一个面上,定义蒙板的黑色部分在渲染时呈现透明状态,而白色部分呈现不透明状态(图6)。这样,无论是多么复杂的模型,均可以十分方便地制作出来了,仅需制作一张黑白的图片即可。
4 结论
通过以上优化方法,可以减少模型中大多数的面,我们尝试优化了系统的场景中的几个物体,模型面数大约平均减少了70~80%左右,优化效果非常显著,而且即使经过这样大量精简构成模型的三角面,仍能保证物体在视觉上的真实感和平滑度而不至于失真。
[1] 彭群生,鲍虎军,金小刚.计算机真实感图形的算法基础[M].科学出版社,2002.
[2] 张攀,周庆龙.VRML三维模型文件的优化技术[J].后勤工程学院学报,2005,02.
TP311
A
1009-0134(2010)09-0088-04
10.3969/j.issn.1009-0134.2010.09.26
2010-03-05
武汉市科技攻关项目“桥式起重机虚拟操纵系统研究与开发”(200711021381);国家检验检疫局科技计划重点项目“桥(门)式起重机作业人员仿真操作培训考核专家系统”(20070K0229)
肖文(1970 -), 男,讲师,在读博士,主要从事计算机仿真研究。
