倒立摆的自调整模糊控制器设计及稳定性分析

杨桂华，陈 静

YANG Gui-hua, CHEN Jing

（桂林理工大学 机械与控制工程学院，桂林 541004）

倒立摆的自调整模糊控制器设计及稳定性分析

The design of inverted pendulum’s adjustable fuzzy controller and its stability analysis

杨桂华，陈 静

YANG Gui-hua, CHEN Jing

（桂林理工大学 机械与控制工程学院，桂林 541004）

本文针对倒立摆多变量的系统特性，提出双模糊控制器设计方案，分别对倒立摆的摆角和小车位移设计模糊控制器。然后根据摆角的不同进入不同的控制阶段，调整两个控制器的输出权重，实现倒立摆的平衡控制。实验证明用Matlab实现的控制算法在对倒立摆的控制中表现出很好的控制效果。

模糊控制；倒立摆；Matlab

0 引言

倒立摆系统是一个比较复杂的不稳定、多变量、带有非线性和强耦合特性的高阶机械系统，它的稳定控制是控制理论应用的一个典型范例[1]。倒立摆系统存在严重的不确定性，一方面是系统参数的不确定性，另一方面是系统受到不确定因素的干扰。通过对它的研究不仅可以解决控制中的理论问题，还可将控制理论涉及的相关主要学科：机械、力学、数学、电学和计算机等进行综合应用。

近些年来，国内外不少专家、学者一直将它视为典型的研究对象，提出了很多控制方案，对倒立摆系统的稳定性和镇定问题进行了大量研究，都在试图寻找不同的控制方法实现对倒立摆的控制[2,3]。模糊控制作为一种智能控制方法，在控制领域发挥着重要的作用，尤其是针对一些不确定的系统，然而传统的模糊控制方法在应用中也有一些局限性，如多变量模糊控制系统，可能的控制规则数随着输入变量的增加而呈指数增加[4]，使得控制器的设计非常复杂，也不适合实时性要求较高的场合。本文针对直线一级倒立摆控制系统多变量特性，采用双闭环模糊控制器设计方案，实现对倒立摆的摆角和小车位移控制。

1 倒立摆的数学模型

在忽略了空气阻力，各种摩擦之后，可将一级倒立摆系统抽象成小车和允质杆组成的系统，如图1所示。

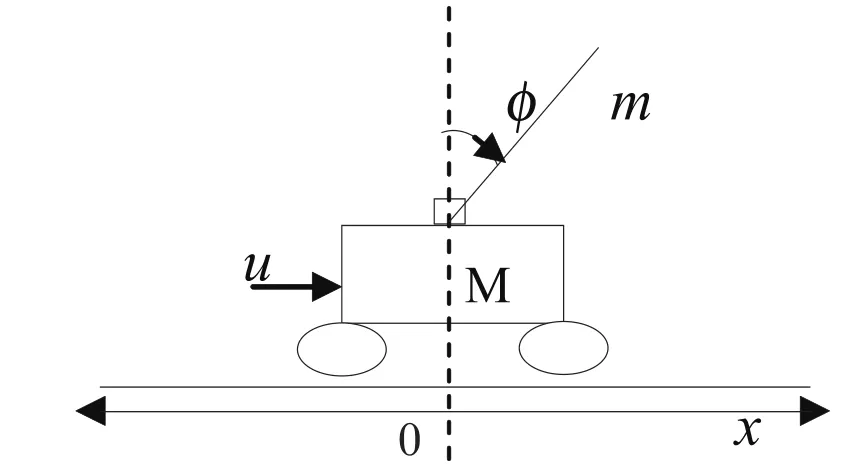
图1 倒立摆系统示意图

图1中φ为摆杆与垂直向上的夹角(rad)，x为小车的水平位移(m)，小车质量M，摆杆质量m，半杆长l，摆杆转动惯量I，u为加在小车上的控制量。运用牛顿力学定律建立系统运动方程，消掉中间变量，并将方程在平衡点(φ=0,x=0 )附近线性化处理，经整理得到倒立摆系统的状态方程如下[5]：

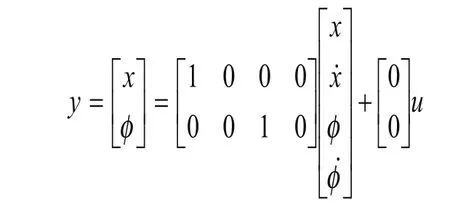
2 倒立摆模糊控制器设计

2.1 模糊控制方案

由倒立摆系统数学模型，倒立摆系统是一个具有两输出变量的不稳定系统，按照传统模糊控制设计方法[6]，一个两输入的模糊控制器不可能实现对输出变量摆角和小车位移的控制，得需要一个四输入的模糊控制器。对于多变量模糊控制系统，由于可能的控制规则数目是输入变量数的指数，但模糊规则的建立给系统的设计带来了很大难度[7]，为此，本系统采用双闭环的模糊控制器控制策略，如图2所示。

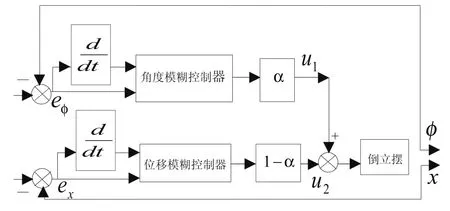
图2 模糊控制系统结构图

2.2 模糊控制器设计

由图2，该控制系统由摆角控制回路和位移控制回路双闭环控制回路构成，分别独立设计角度模糊控制器和位移模糊控制器。

2.2.1 角度模糊控制器设计

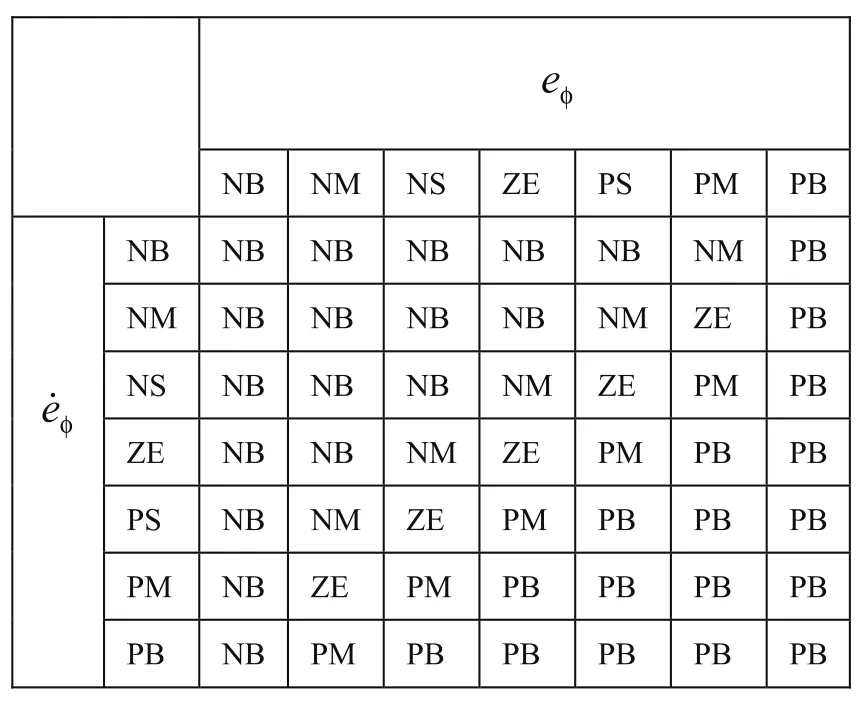
表1 角度模糊规则集

2.2.2 位移模糊控制器设计

小车位移模糊控制器的两个输入变量为位移偏差ex和位移偏差变化率，其中 论域为[-0.3,0.3]，论域为[-1,1]，分别定义5个模糊子集{NB,NS,ZE,PS,PB}，输出u2控制论域为[-2.4，2.4]，分割成5级模糊子集，分别为{NB,NS,,ZE,PS,PB}，量化等级为{-2.4,-1.2,0,1.2,2.4}。选择输入量的隶属函数为三角形（trimf）。输出u2的隶属函数为单点常数。根据电机输出力的大小与小车位移、速度的关系，小车位移模糊控制规则库如表2所示，考虑到有些情况不允许发生，不设定模糊规则，如小车位移为NB的同时小车速度为NB的状态不可控，应预先加以调整。设定模糊决策采用Mamdani型推理算法，解模糊用重心平均法。

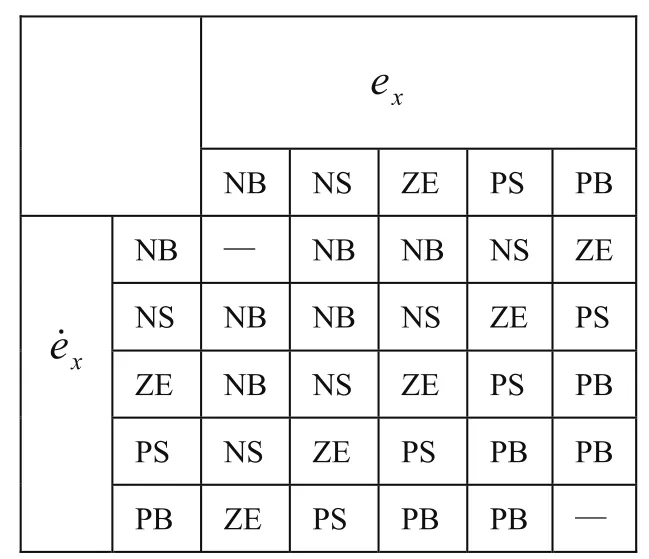
表2 位移模糊规则集

3 控制效果分析

选用固高科技（深圳）公司的GLIP2001型直线一级倒立摆作为实验平台，实际控制系统的模型参数如下：

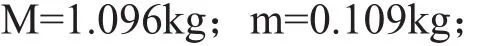
b=0.1N/(m.s)；I=0.0034kg*m*m;在simulink环境下构建模糊控制系统，完成系统中各参数的整定，即系统中加权系数a取0.3，比例因子ke,kecku对控制效果的影响很显著,因而对量化因子的优化设计就显得非常重要[8]，经过大量仿真实验，确定最理想的一组参数：角度模糊控制器输入比例因子kφ=0.8，keφ=0.95， 输出比例因子ku1=5。位移模糊控制器输入比例因子kx=1，kex=0.5，输出比例因子ku2=5。根据实际系统参数及状态方程，在matlab环境下编写控制程序，进行仿真试验研究，双模糊控制器的输出权重经过不断地试验得到，仿真后的系统输出曲线如图3，图4所示。

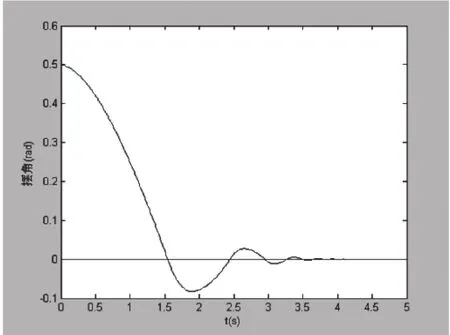
图3 倒立摆偏角仿真曲线

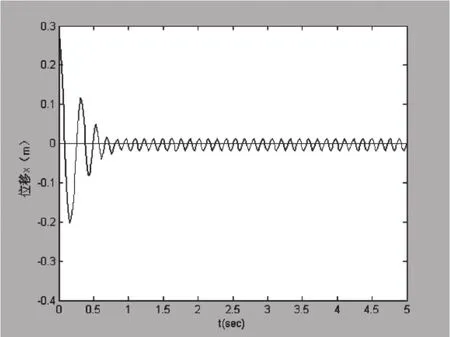
图4 倒立摆位移仿真曲线

本次试验是在初始状态 T下起摆，由仿真曲线可知，摆杆随后一直处于倒立位置,角度偏差几乎为零， 小车位置保持在平衡位置附近来回移动, 其控制效果比较理想。

4 结束语

所设计的单级倒立摆控制系统在摆杆偏离垂直站立角度一定范围时，自动启动起摆模糊控制算法，再次使其稳定在垂直站立状态。本文通过合理地设计模糊控制器的各个输人量和输出量的论域、控制规则及其它重要参数, 在Matlab平台上建立倒立摆的仿真模型，得到了理想的仿真曲线。

[1] Meier,H.,Zu.Farwig,Unbehauen,H.Discrete computer control of a triple_inverted pendulum[J].Optimal Control Apple cations & Methods.1990,11(2)：157-171.

[2] K.Furuta,Katsuhisa,H.,Kaijiwara and K.Kosuge.Digital control of double inverted pendulum on an inclined rail[J].Int.J. of Control,1980,32(5)：907-924.

[3] Eltohamy K G,Kuo C Y. Real-time Stabilization of a Triple-link Inverted Pendulum Using Single Control Input[J].IEEE Proc-Control Theory.1997,144(5)：498-504.

[4] 杨世勇,王培进,徐莉苹.倒立摆的一种模糊控制方法[J].自动化技术与应用.2007,26(7)： p10-12.

[5] 固高科技(深圳)有限公司.固高摆系统与自动控制实验[Z].2002.

[6] 廉小亲.模糊控制技术[M].中国电力出版社.2003,8.

[7] 陈莉,陈华,谢丽蓉.直线一级倒立摆模糊控制器设计[J].兰州大学学报(自然科学版).2008,7(44)：295-296.

[8] 过润秋,洪旭,苏旺旺.基于模糊控制理论的二级倒立摆控制算法[J].西安电子科技大学学报(自然科学版).2006,33(1)： P111-P115.

TP273

A

1009-0134(2010)09-0072-03

10.3969/j.issn.1009-0134.2010.09.21

2009-10-30

广西科学基金项目（桂科自0991252）

杨桂华（1971 -），广西兴安人，讲师，研究生，研究方向为计算机测控技术。