对双摆线钢球行星传动减速器的研究

王向华，吕锦辉

（1.山西省特种设备监督检验所，山西 太原 030002；2.山西北方风雷工业集团有限公司，山西 太原 030009）

对双摆线钢球行星传动减速器的研究

王向华1，吕锦辉2

（1.山西省特种设备监督检验所，山西 太原 030002；2.山西北方风雷工业集团有限公司，山西 太原 030009）

文章以“滚动传动——结构简单”为基本思想，以研制国产减速器为目标，进一步对“K－H－V双摆线钢球行星传动减速器”进行研究，根据摆线的形成过程，分析KH－V双摆线钢球行星传动机构的传动原理与组成，解决内外摆线啮合传动中的干涉问题，同时也减少内外摆线的磨损、增大接触面积、提高承载能力和传动效率。

行星传动减速器；双摆线；滚动体

行星齿轮减速器包括渐开线行星齿轮减速器、摆线针轮减速器、谐波减速器等。该减速器的最大特点是传动效率高、传动比范围广，传动功率可从10～50 000 kW，体积和重量比普通齿轮减速器和蜗杆减速器要小得多。行星传动减速器主要应用了传动机构中的一个或几个构件既公转又自转的复合转动而达到减速的目的。2 K－H、K－H－V是常用的两种行星传动机构。行星传动减速器在保证各齿轮直径相差不大的情况下获得较大的传动比，因而结构紧凑，体积小。K－H－V机构还具有构件数目少、传动链短、装配方便等优点，存在的主要问题是内齿啮合容易发生啮合干涉。两齿轮的齿数差愈小，发生啮合干涉的可能性就愈大，行星轮运动时产生的离心力和离心力矩不容易得到平衡，再加上偏心输出机构，致使它的传动受到一定限制。

用摆线齿廓取代渐开线齿廓，并将中心轮的轮齿改成圆柱销（针轮），即形成摆线针轮行星减速器。和内啮合的渐开线齿廓相比，摆线齿廓没有干涉。传动中同时啮合的齿数多，因而重叠系数大，过载能力高；运转平稳振动小、噪声低、传动效率高；传动比大而且范围宽、体积小、重量轻、使用寿命长。尽管摆线针轮行星减速器有许多优点，然而就整体而言，受其结构的限制，它的承载能力还是比较低，散热条件差、温升高；摆线轮加工比较困难，针轮结构也较复杂。因此，关于摆线针轮行星减速器的研究还在发展之中。虽然目前已经研制了一些工作性能都比较高的行星传动减速器，但共同的缺点是结构复杂化了，增加了制造难度，成本提高，得不到广泛使用。

1 行星传动原理

由于钢球摆线减速器的基本原理类似行星传动的原理，所以先介绍行星传动的原理。

在轮系中，如果其中有一个或几个构件的轴线的位置不是固定的，而可以绕其他齿轮的固定轴线回转，则这种轮系称为周转轮系。见图1，外齿轮1和内齿轮3均可绕固定轴线O1、O2回转。套装在构件H上的齿轮2既可以绕自身轴线O2自转，又可随构件H绕OH公转。一般称齿轮1、3为中心轮，齿轮2为行星轮，构件H为系杆。

对于图 1（a）自由度为 F＝3×4－2×4－2＝2，称为差动轮系；

对于图 1（b）自由度为 F＝3×3－2×3－2＝1，称为行形星轮系。

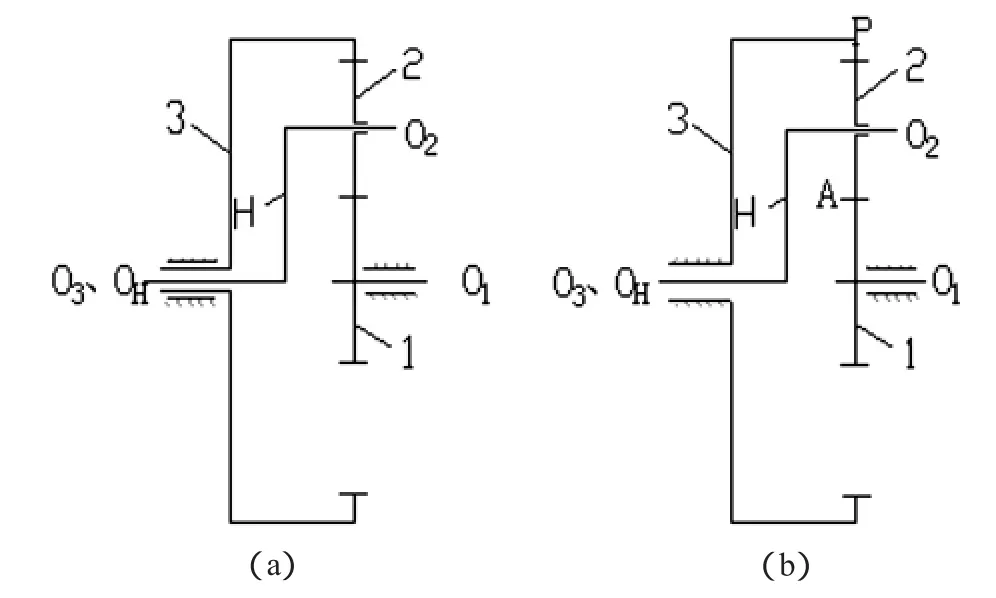
图1 周转轮系的基本结构

由图1可以看出，基本的行星轮系有3个基本的构件，两个中心轮用K表示，一个系杆用H表示，简称2 K-H机构。在这种机构中，固定两个中心轮的任一个，则运动可由另一个中心轮和系杆随意输入、输出，实现传动的目的。按照行星传动机构组成的基本要求，可对基本的行星机构3个基本的构件作适当的演化。如在图1（b）中，取掉中心轮1、3的任一个，以系杆H和行星轮2作为主动件或从动件，也可实现传动的目的。但因行星轮2作平面运动，动力必须通过能够传递平行轴之间的旋转运动的联轴器（偏心输出机构）来传递。一般用V表示偏心输出机构，则把这种行星轮系简称K－H－V行星传动机构，见图2。

图2 K-H-V行星传动机构

行星轮系传动比的计算有好几种方法，如转化机构法、角位移变化分析法、列表法等。根椐速度瞬心法亦可方便的求出传动比。

对于图1（b）中的2 K－H机构，行星轮2沿固定齿轮3内圈作纯滚动，则啮合点P就是行星轮2的速度瞬心。

轮1与轮2的啮合点A的速度Va为：即 r1w1=2r2w2

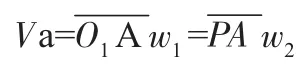
轮2与系杆H的联接点的速度Vo2为：即 r2w2=（r1+r2）wH

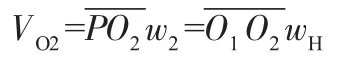
由几何结构关系：

2（r1+r2）=r1+r3

联立以上各式解之：

同理，对于图2中的K-H-V机构，轮2与系杆H的联接点O2的速度V为:即 （r1-r3）wH=r2w2

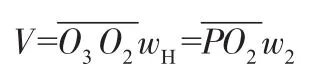
式中：r：各轮半径

Z：各轮齿数由式（2）可以看出，中心轮和行星轮齿数差愈小，传动比愈大。与2 K-H机构相比较，K－H－V行星传动机构结构简单，而且能获得较大的传动比，所以，K-H-V行星传动机构得到广泛的应用。在K-H-V行星传动机构的基础上，采用不同的结构形式啮合齿廓曲线就形成了不同的K－H－V行星传动机构。如摆线针轮行星传动、链条圆弧齿传动、圆弧针齿传动等。

2 摆线的形成

2.1 按无包心形成内外摆线

见图 3，设两个大圆（定圆、基圆）O1、O2半径为 R1、R2，两个小圆（动圆、滚圆）O3、O4半径均为rO。当滚圆O3在基圆O1圆周外作纯滚动时，滚圆上点C的轨迹称为外摆线，见图3（a）。当滚圆O4在基圆O2圆周内作纯滚动时，滚圆上点D的轨迹称为内摆线，见图 3（b）。

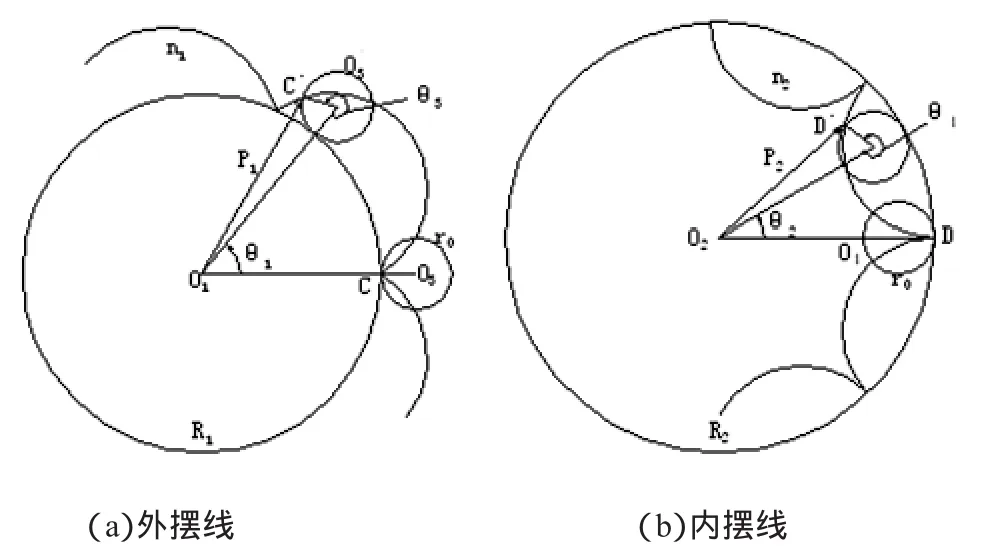
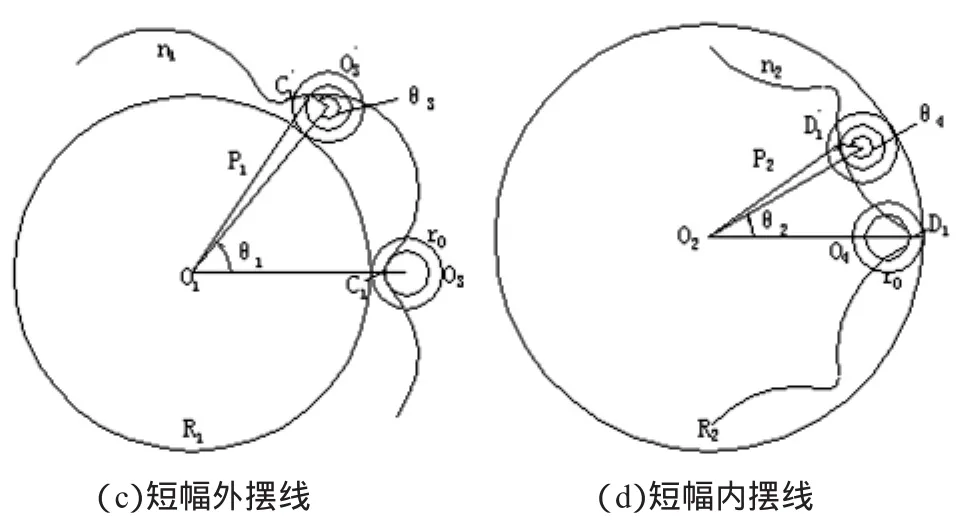
图3 摆线的形成原理

从图中可以看出，摆线是以滚圆自转角θ3、θ4等于2 π为周期的循环曲线。若令：

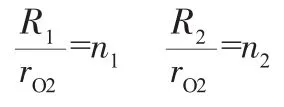
那么，要在基圆上形成一条封闭的具有n1、n2个完整周期的摆线，则n1、n2必须为整数n1、n2称为内外摆线波数。

同时也可以看出，滚圆上任何其他的点都不可能形成和C、D的轨迹完全重合的摆线。这表明，按无包心形成内外摆线时，动点数C、D是唯一的。

若在滚圆内固结一点C1（D1），并使(短幅系数)，这样，当滚圆在基圆上作纯滚动时，C1、D1点的轨迹称为短幅摆线，见图 3（c）、（d）。

2.2 按有包心形成内外摆线

见图 4，设圆 O1、O2半径为 R1、R2；圆 O3、O4半径分别为 R3、R4。当滚圆O2在基圆O1圆周外作纯滚动时，滚圆上点E的轨迹称为外摆线，见图4（a）。当滚圆O3在基圆O4圆周内作纯滚动时，滚圆上点F的轨迹称为内摆线，见图4（b）。

图4 有包心形成内外摆线

同理，若在滚圆圆周外固结一点，则该点的轨迹称为短幅内外摆线。

3 摆线齿廓的啮合原理

由上一节可知，摆线可按有包心和无包心两种方法形成，在满足一定条件时，两种形成法形成的摆线是等效的。

在图5所示的有包心形成法形成外摆线的过程中，开始动圆上的E点与基圆上的P点重合，因动圆较大，那么在动圆上取一点E1，并使动圆上的EE1等于基圆上的PP1，则当动圆逆时针转动时，E1一定与P1相重合，并且E1点一定在E点所形成的外摆线上。由此，在动圆上取若干点 E1、E2、E3、……，并使 EE1＝E1E2＝E2E3＝……。当动圆连续纯滚动时，E、E1、E2、E3……等点的轨迹是一致的，即形成一条连续的外摆线。这表明，按有包心形成外摆线时，E、E1、E2、E3……等点是等效动点。现设形成的外摆线的波数为n1，动圆上的等效动点数为Z1，则有：

图5 有包心形成外摆线的过程

同理，设形成内摆线的动点数为Z2，摆线的波数为n2，则有Z2=n2-1

这表明，n波连续的一条封闭的摆线上有n±1个等效动点。

从图5可以看出：①P、P1、P2……各点是一波摆线在基圆上的起、终点，它们均布于基圆上，等效动点E、E1、E2……是动圆与所形成的各波摆线的交点，它们均布于动圆上，这里定义动圆为“动点圆”。②由等效点E、E1、E2……等形成的摆线在这些点处的法线都通过基圆上的P点，也就是说，过等效动点的法线比交于同一点。动圆和基圆的连心线亦通过P点，所以总有常数。因此，等效动点与摆线啮合能满足啮合基本定律的条件，保证实现定传动比传动。

4 双摆线的啮合传动

前面分析中，我们对等效动点的形状未加任何限制条件，因此它可以是任何曲线，据此，得到这样的结论：若用摆线作啮合轮廓，要保证获得定传动比传动，则与摆线按星形传动原理啮合的任何齿廓的动点圆应与摆线形成中的自身动点圆相重合，并且动点数相等。

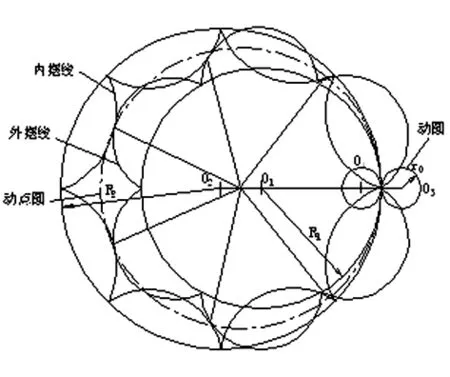
图6 双摆线的啮合过程

按此结论，一条内摆线与一条外摆线必能按行星转动原理进行啮合传动。见图6，其实现定传动比和连续传动的必要条件是：

这里，rO：按无包心形成内外摆线时的动圆半径。

由式（1）、（2）可知，双摆线啮合是两齿差的行星传动。

啮合过程的实质是：形成内外摆线的两基圆按偏心距为2 rO配制（相切）后，两基圆作纯滚动时，内外摆线各自的动点圆重合作平面运动。动点圆圆心位于两基圆连心线的中点，动点圆的半径动点即为内外摆线的啮合点均布于动点圆上，动点数

5 结论

由图6也清楚地看出：内外摆线除在啮合点（动点）处相切，还有若干相交点，因而在实际传动中，内外摆线发生严重的干涉。由此可知：内外摆线很难在同一平面内按行星传动原理进行啮合传动。为此，把内外摆线刻制在两个平盘的表面上，配制后组成一条循环滚道，按动点数放入滚动体（钢球），使内外摆线间接啮合。这样既解决了内外摆线啮合传动中的干涉问题，同时也减少内外摆线的磨损、增大接触面积、提高承载能力和传动效率。

[1] 张彩丽，李思益，张浩，摆线钢球减速器输入机构力学模型的建立与分析[J].现代制造工程，2004（8）:85-87.

[2] 周建军，摆线钢球行星传动机构简介[J]机械设计与研究；1997（2）22-23.

[3] 高东强，姚素芬，李进.基于PRO/E的双摆线钢球减速器的参数化设计技术的研究[J]机械设计与制造，2009，(03).

Research on the Planetary Gear Reducer of Double Cycloid Ball

Wang Xianghua，Lv Jinhui

The article，taking“rolling drive-simple structure”as the basic idea,and developing domestic reducer as the target gear,further does research on “K-H-V planetary gear reducer of double cycloid ball”.Basing on the formation process of cycloid，the article analyzes driving theory and composition of planetary gear mechanism of K-H-V double cycloid，addresses the interference problems of external and internal cycloid gear.In this way，we can reduce wear and tear of external and internal cycloid，increase the contact area,and improve the carrying capacity and transmission efficiency.

planetary gear reducer；double cycloid；rolling object

TH132.46

A

1000-8136(2010)35-0030-03