MIMO信道容量的隐训练序列分析法

邢开开

(桂林电子科技大学信息与通信学院,广西桂林 541004)

0 前言

在无线MIMO系统中,有关空时译码和解调部分的许多工作都是基于信道的状态信息在接收端是有效的前提下完成的[1-2]。通常在研究一种空时编码和调制算法的性能时,一般是假定信道服从某种己知的统计分布(高斯、瑞利或莱斯)[3],这样仿真得到的是该算法的理论性能。然而,在实际应用中或在对某种空时编码和调制算法的实际性能进行评估时,必须对真实信道的状态信息进行合理的估计,而估计的效果或精度,将直接影响系统的真实性能。尽管目前信道估计可以使用一些非数据的辅助技术或盲技术,当然也有完全避免发送训练序列和信道估计的技术,例如酉空时编码调制和差分空时编码调制,但研究表明使用这些技术会或多或少地使系统的性能下降。所以目前还有许多数字通信系统(拟平稳的平坦衰落信道),仍然使用一些数据辅助技术,例如利用训练(导频)序列去探测信道,原因有两点:一是因为使用这项技术来获得信道的状态信息简单而有效;二是可以减少系统性能的不必要的损失。

本文基于隐训练序列的信道估计模型,无需为训练序列专门分配时隙,可在没有带宽损失的情况下有较高的估计精度和低计算复杂度,有利于实时估计,切实可行。又利用最小二乘算法,仿真并分析信噪比、数据传输的帧长、收发天线的数目与信道容量下限的变化关系。

1 系统模型

设信道为平坦衰落的窄带信道,并服从简单的离散时间、块衰落,即某个离散时间间隔 T内,信道系数不变。隐训练序列情况下,信息流帧结构如图1所示,一帧占有时间为T,有 2T个符号,并且由训练符号 P和数据符号 D组成,可表示为S=[Sp,Sd]T,一帧(T个符号的块)内,MIMO信号模型可表示为

图1 隐训练序列情况下信息流的帧结构示意图

其中,Y为2T×N维接收复数信号矩阵;N代表接收天线数;ρ为每根接收天线上的信噪比;S为2T×M维发射复数信号矩阵,平均能量为1;M为发射天线数;H为连接发收天线的复数信道矩阵;V为2T×N维加性复数噪声矩阵;H和V的元素为独立的复高斯随机变量,均值为0,方差为1。

2 估计算法

假定在Tp时间内发送了训练符号矩阵Sp,并为接收机所知,由式(1)可得到下列关系

式中,ρp为训练阶段每根接收天线的信噪比;Yp∈CTp×N为接收的训练数据矩阵。

发射功率在训练和数据传输期间可能不同。训练就是要利用Sp和Yp去产生信道的估计值 即:

最小二乘估计是指以误差的平方和最小的参数为估计值。由上述条件可推知误差的平方和为:

式中ε=Yp-

化简得到:

3 信道容量下界

假设各天线功率均匀分配,则基于训练序列的信道估计的信道容量 Cp可定义为[4-5]:已知发射信号Sp、接收信号Yp和Yd与未知发射信号Sd之间的互信息关于发射信号Sd分布的最大值,用数学公式表示如下:

其中,“sup”表示上确界;I(Yp,Sp,Yd;Sd)=I(Yd;Sd/Yp,Sp)+I(Yp,Sp;Sd)。

由于Sd与Sp和Yp无关,所以上式中的最后一项:I(Yp,Sp;Sd)=0[6],因此得到:

因此,信道容量Cp可以看成是在给定发射和接受训练数据Sp和Yp的条件下,发射信号Sd和接受信号Yd之间的互信息关于Sd分布的上确界[5],即:

其中V′d为加性噪声和信道误差项之和。其归一化方差为:

其中,“tr”为矩阵积运算符;“E”代表求数学期望,下同。如果这时考虑 V′d对数据传输造成的最坏影响,便可得到基于训练序列估计的信道容量的一个下限,即:

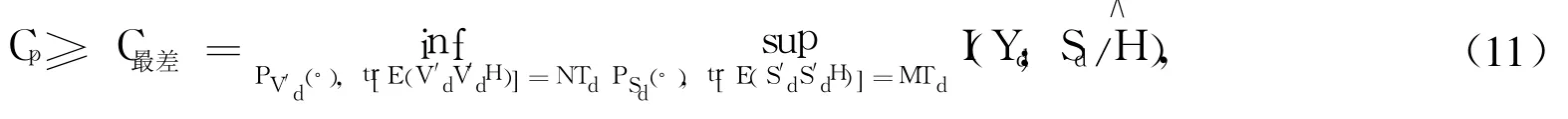
其中“inf”表示下确界。

令Rs=E(SHS)和Rv=E(VHV),可以把式(1)所示的信道容量计算公式推广为:

其中,“det”为行列式运算符;“log”为对数运算符,下同。在最坏情况下,由式(1)所示的加性噪声信道的信道容量下限为:

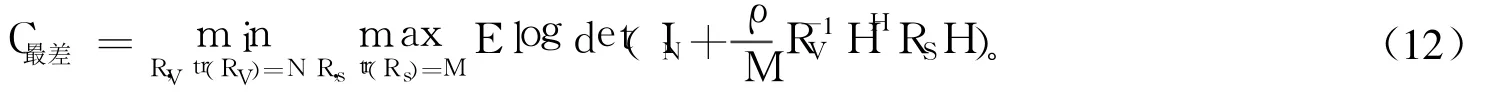
式(12)说明基于训练序列的信道估计的信道容量的下限可以用一个零均值、受相同功率限制的加性噪声取代V′d来得到。由于E(Sd)=TdRs,式(10)变成:

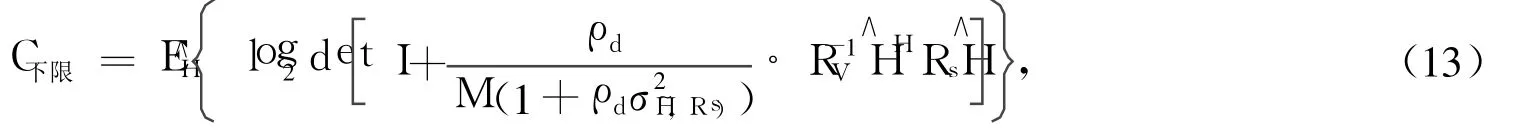
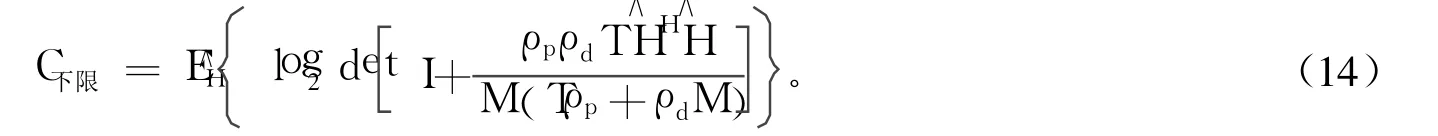
假设发射训练序列和传输数据的功率相等,即ρd=ρp,简化式(14)得到:

由上述分析,可以得出基于LS算法估计的信道容量与信噪比、收发天线数和数据传输的帧长T的变化关系,如图2图4。图2图4中“训练序列”是文献[4]中的结果。

从图2可以看出:当M=N=2,T=100,采用训练序列得到的信道容量的下界与信噪比成正比关系。并且得出采用隐训练序列得到的信道容量下限要比直接采用训练序列得到的容量下限要大,其差值也随信噪比成正比关系。

取ρd=ρp=18 dB,T=100,N=2,两种类型的训练序列得到的信道容量下限与发射天线数目的变化情况见图3。从图3可以看出:采用隐训练序列得到的信道容量下限比直接采用训练序列得到的容量下限大,体现了隐训练序列的优越性能;也可以看出收发天线数量的无限增加并不一直能带来信道容量下限的增大。

取ρd=ρp=18 dB,M=N=2,两种类型的训练序列得到的信道容量下限与传输数据帧长的变化情况见图4。从图4可以看出:增大传输数据的帧长能够提高信道容量下限,同文献[4]比较,发现在相同的条件下,采用隐训练序列能较大提高信道容量,这是由于隐训练序列无需专门为其分配时隙且没有带宽损失。

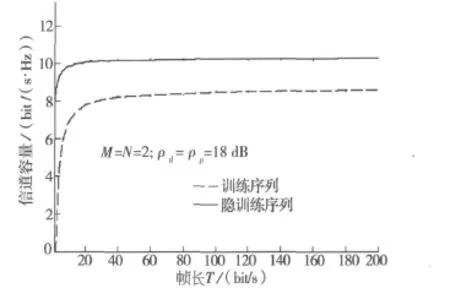
图4 信道容量随帧长变化关系图

4 结束语

本文基于一种隐训练序列的MIMO信道估计模型,推导出最小二乘方法对信道系数进行估计的公式以及容量的下限,并同文献[4]比较仿真了当发送训练序列和数据传输的功率相等时,信噪比、数据传输帧长及收发天线数目与信道容量下限的变化关系。数值模拟结果表明:相同条件下,不恰当的天线数目并非一定能提高信道容量,采用隐训练序列要比直接采用训练序列在很大程度上改善系统的性能,能较大提高信道容量。

[1] Telatar IE.Capacity of Multi-antenna Gaussian Channels[M].[S.l.]:Bell Labs TechnicalMemorandum,1995:1-28.

[2] Foschini G J,Gans M J.On Limits of Wireless Communications in Fading Environment When Using Multip le Antennas [J].Wireless Personal Communications,1998(6):311-335.

[3] Alamouti SM.A Simple TransmitDiversity Technique forWireless Communications[J].IEEE JSAC,1998,6(8):1451-1458.

[4] Hassibi B,Hochwald B M.How Much Training is Needed in Multiple Antenna Wireless Links[J].IEEE Transactions on Information Theory,2003,49(4):951-963.

[5] Cover T M,Thomas JA.Elements of Information Theory[M].New York:John Wiley＆Sons,1991.

[6] 仇佩亮.信息论及其应用[M].杭州:浙江大学出版社,1999.

[7] VosoughiA,Scaglione A.The Best Training Depends on the Receiver Architecture[C]//Proc IEEE ICASSP′04,2004:409-412.

[8] Scaglione A,Vosoughi A.Turbo Estimation of Channel and Symbols in Precoded MIMOSystems[C]//Proc IEEE ICASSP′04.2004:413-416.

[9]Tugnait J K,Luo W.On Channel Estimation Using Super-imposed Training and First-order Statistics[J].IEEE Communications Letters,2003,7(9):413-415.