一种单负材料对的反射型带阻滤波器

张振辉，王政平，赵嫔嫣

(1.哈尔滨工程大学理学院，哈尔滨150001，zhangzhenhui01@163.com;2.黑龙江大学集成电路重点实验室，哈尔滨150080)

Metamaterials是一类由人工设计实现均匀性的、具有特异电磁性质的材料.其中包括介电常数与磁导率同时为负值的双负材料［1］(double-negative materials，NG)、单负材料［2］(single-negative materials，SNG)(其中包括电单负材料(epsilonnegative materials，ENG)和磁单负材料(Mu-negative materials，MNG)).相应地，介电常数与磁导率同时为正值的材料被称为双正材料(doublepositive materials，DPS).Metamaterials具有的特异电磁性质已引起了许多人的研究兴趣.Mandel’shtam［3］首次介绍了负折射现象.Veselago指出了双负材料所具有的一系列反常电磁特性，如负折射、反多普勒效应、反切仑柯夫辐射等.很多研究者也投入到对单负材料上的研究［4－5］.Alù和Engheta等人对由ENG和MNG组成的成对双层结构进行了研究，利用等效传输线方法分析了这种双层结构形成共振隧穿需要的条件，并指出了这种结构在一定条件下具有透明、隧穿和共振的现象，从而为单负材料对结构在微波器件中的应用奠定了理论基础.本文建立了一种基于单负材料对的反射型带阻滤波器的物理模型，提出了这种滤波器的设计原理与方法，并对各相关参量对其滤波性能的影响进行了数值仿真.

1 物理模型及其原理

1.1 物理模型

众所周知，电磁波在SNG材料中传播时其波矢是复数，因而在SNG材料中只存在倏逝场.电磁波在其中是迅速衰减的(换言之是不透明的).但是如果将ENG材料和MNG材料组合在一起构成“单负对”结构，则在一定条件下电磁波是可以通过的.单负对结构的这种性质可用于构造某些微波器件.

本文提出的由双层SNG材料构成的反射型带阻滤波器的结构模型如图1所示.其中，0区是空气;1区由ENG材料构成.其中，ε1＜0，μ1＞ 0;2区由MNG材料构成.其中，ε2＞0，μ2＜0; 3区由金属板构成.

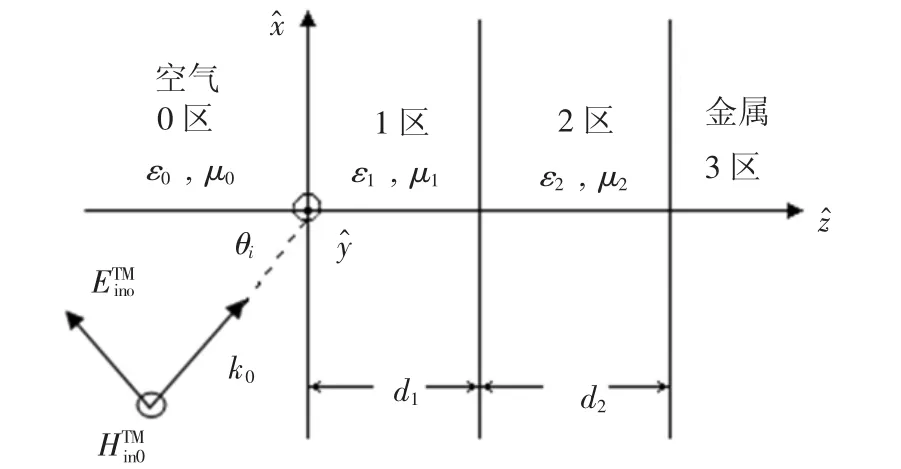
图1 双层单负材料对的结构示意图

本文仅仅考虑ENG材料和MNG材料是各向同性、均匀、损耗的介质.当材料具有明显的损耗效应时，可以在某一频率范围内吸收入射的电磁波能量并实现整体结构的反射率为零;其它频率的电磁波则在结构表面发生反射.

1.2 工作原理

Caloz等［6］指出可利用传输线理论来等效地描述电磁波在metamaterials中的传播特性.无损耗的 metamaterials的传输线等效模型如表 1所示.

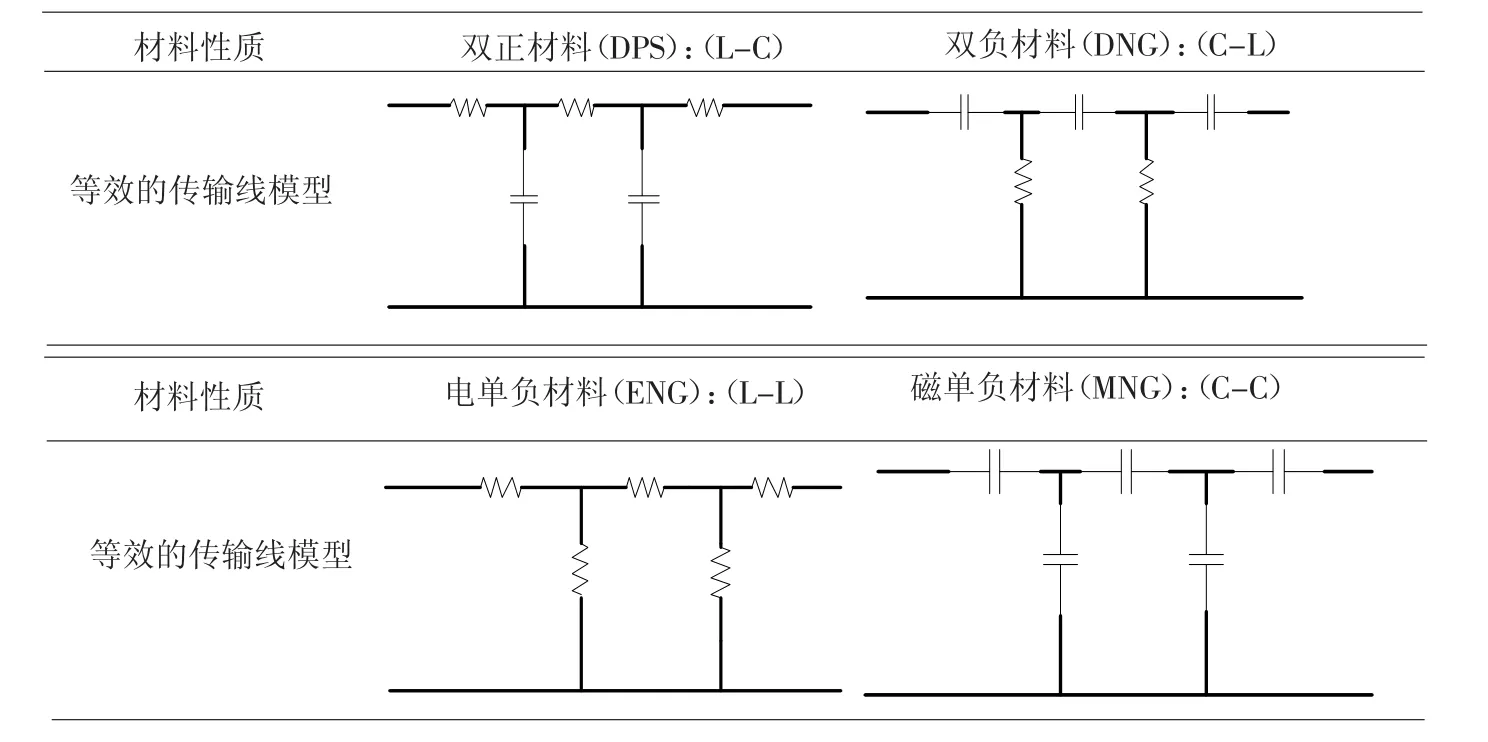
表1 各种无损耗metamaterials的等效传输线模型

由于提出的反射型带阻滤波器设计要求其构造材料是有损耗的，所以本文在上述无损耗等效传输线模型中引入相应的电阻和电导，以构成有损耗metamaterials的等效传输线模型，如表2所示.

根据表2所示有损耗metamaterials的等效传输线模型，结构的传输线模型如图2所示.

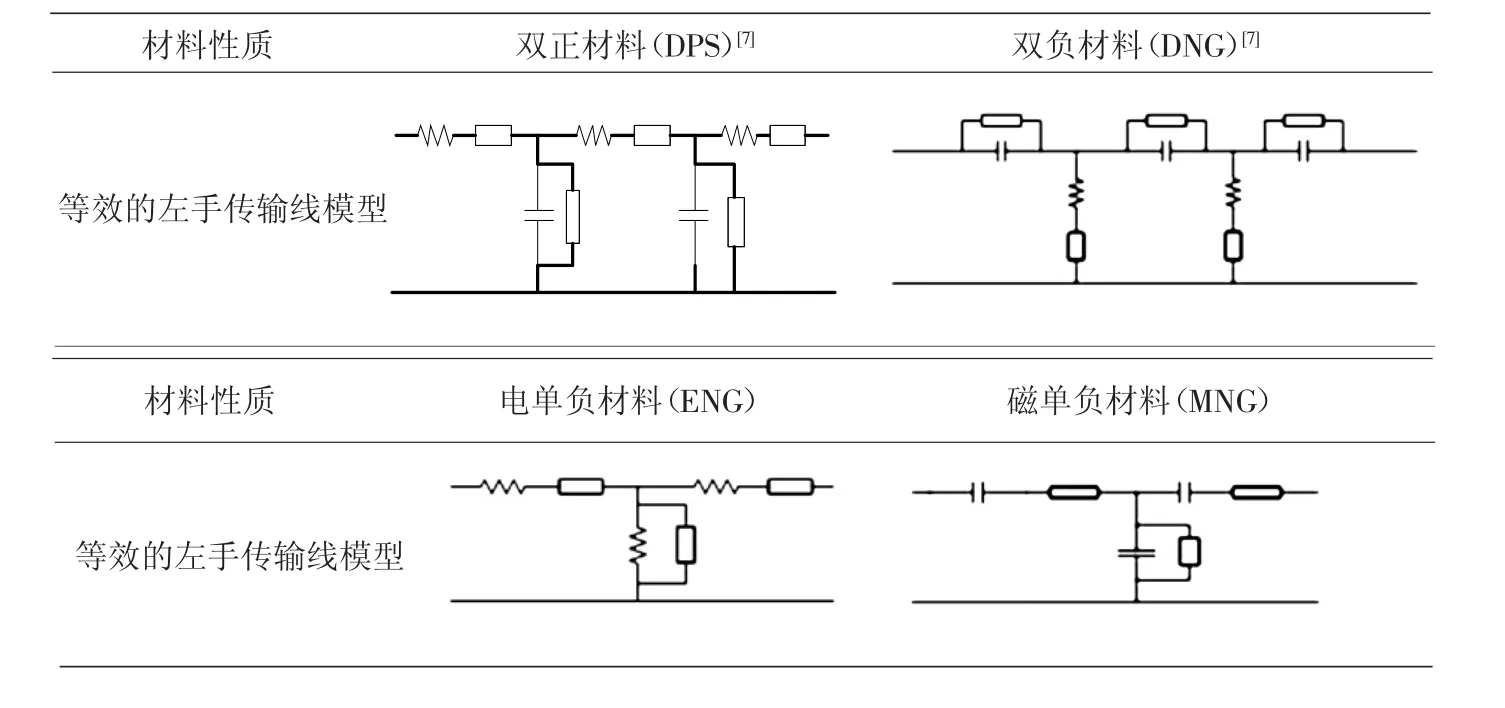
表2 各种损耗性metamaterials的等效传输线模型

根据图2所示的传输线模型可求得这种结构 的等效输入阻抗为

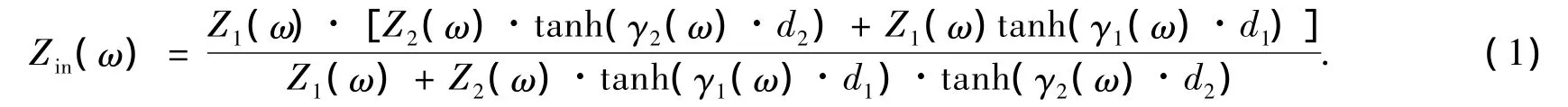
式中:Z1(ω)，Z2(ω)分别为两种单负材料结构本身的特性阻抗，d1，d2分别为传输线结构的单元厚度(单负材料层的厚度)，γ1(ω)，γ2(ω)分别为电磁波在ENG和MNG中的传播常数，γ(ω)可以表示成γ(ω)=α(ω)+iβ(ω)，其中，α(ω)为衰减常数，β(ω)为相移常数［8］.则反射率R可表示为

图2 双层单负材料对结构的等效传输线模型

在工程上通常用反射损失表示其反射特性并将其表示成dB的形式为

其中，

从式(1)～式(7)中可以看出，层厚度、电感(电容)、电阻(电导)的值会影响这种反射型带阻滤波器的反射率.

2 仿真结果

2.1 层厚度对反射率的影响

设传输线的基本单元结构厚度分别为1 mm，其中，曲线r1为两层单负材料厚度均为1 mm的情况(每层各有1个传输线单元);曲线r2为厚度均为2 mm的情况(每层各有2个传输线单元);曲线r3为厚度均为3 mm的情况(每层各有3个传输线单元).其余的单位长度参量值为:L1= L2=2·10－9H/m，C1=C2=0.5·10－12F/m，R1=4 Ω/m，R2=4.8 Ω/m，G1=0.000 1 S/m，G2=0.000 1 S/m，如图3所示.

从图3可以看出:1)厚度的变化不仅影响中心频率的位置，也会影响反射谱的带宽，且对中心频率位置的影响比较明显;2)厚度为1 mm的带阻性能优于厚度分别为2 mm和3 mm的情况:厚度为1 mm的时候反射损失可以达到45 dB，而2 mm、3 mm的情况反射损失分别仅为4 dB和1 dB;3)当双层介质的厚度不断增加时，带阻特性逐渐变差，且随着厚度的增加反射损失中心频率逐渐向高频的方向移动.

图3 厚度的变化对反射率的影响

2.2 电容值变化对反射率的影响

设传输线的单元结构厚度为1 mm，其中，曲线r1为电容值为C1=C2=0.5·10－12F/m的情况;曲线r2为电容值为C1=C2=0.6·10－12F/m的情况;曲线r3为电容值为C1=C2=0.4·10－12F/m的情况.其余的单位长度参量值为:L1=L2= 2·10－9H/m，d1=d2=1 mm，G1=G2= 0.000 01 S/m，R1=R2=4.8 Ω/m，如图4所示.

从图4可以看出:1)电容值的变化对中心频率的影响明显，对反射谱线的带宽也有影响;2)当电容值增大时反射谱线的中心频率向低频方向移动，当电容值减少时反射率向高频方向移动; 3)存在一个最佳电容值使得反射损耗达到最大，其余电容值将降低反射损耗.适当的选择参数可以使反射带宽达到1 GHz左右.

2.3 电感值变化对反射率的影响

设传输线的单元结构为1 mm，其中，曲线r1为电感值为L1=L2=2.0·10－9H/m的情况;曲线r2为电感值为L1=L2=2.3·10－9H/m的情况;曲线r3为电感值为L1=L2=1.7·10－9H/m的情况，其余的单位长度参量值为:C1=C2= 0.5·10－12F/m，d1=d2=1 mm，G1=G2= 0.000 01 S/m，R1=R2=4.8 Ω/m，如图5所示.

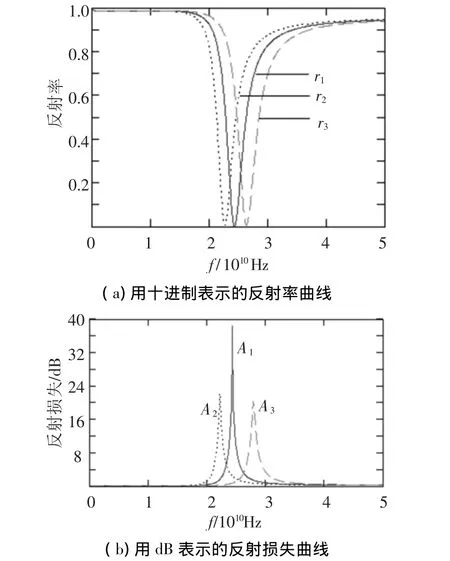
图4 电容值的变化对反射率的影响

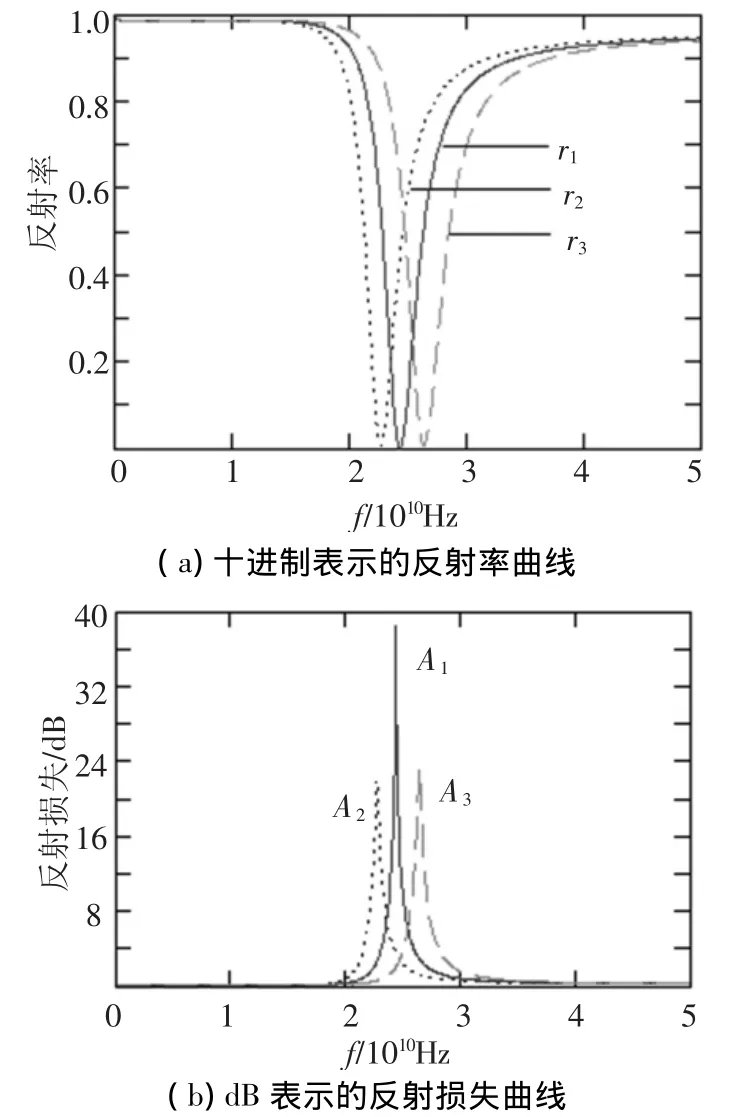
图5 电感值的变化对反射率的影响

从图5可以看出:1)电感值的变化对中心频率的影响很明显，对反射谱宽也有影响;2)当电感值增大时反射谱线的中心频率向低频方向移动，当电感值减少时反射谱线的中心频率向高频方向移动，这点同电容的影响是一致的;3)存在一个最佳电感值使得反射损耗达到最大，其余电感值将降低反射损耗.

2.4 损耗(电阻、电导)值对反射率的影响

损耗(电阻、电导)值对反射率的影响如图6所示.其中，曲线r1为电阻值为R1=R2=3 Ω/m的情况;曲线r2为R1=R2=6 Ω/m的情况.其它的参数参量值为:L1=L2=2·10－9H/m，C1= C2=0.5·10－12F/m，d1=d2=1 mm，G1= G2=0.000 1 S/m.

从图6可以看出:1)电阻的变化对反射谱宽是有影响的;2)增大电阻值时反射率降低，反射谱展宽.

综上所述，电容、电感、材料的厚度、电阻和电导都对反射率有一定的影响，其中，电容和电感值得变化主要对中心频率有一定的影响;电阻和电导的改变主要影响反射率的带宽;厚度既影响带阻滤波器的中心频率也影响带宽.适当的调节参数可以使带阻滤波器的带宽达到1 GHz左右.

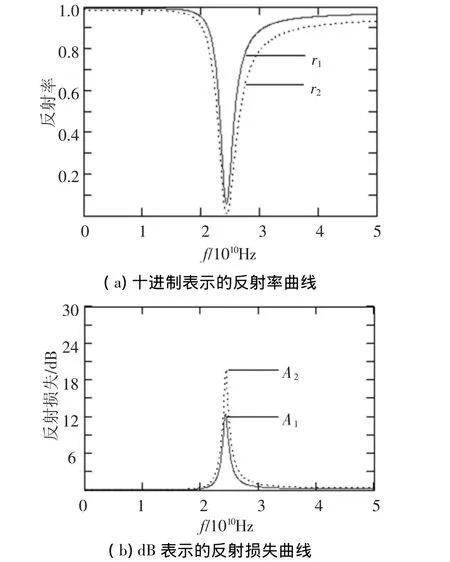
图6 电阻的变化对反射率的影响

3 结论

1)提出了基于单负介质对结构的反射型带阻滤波器的、用等效传输线表征的物理模型;

2)对这种滤波器的界面反射率(及反射损耗)进行了理论推导，指出了这种结构作为反射性带阻滤波器的可能;

3)对影响反射率的因素进行了数字仿真，对仿真结果的物理含义进行了诠释，为其工程设计提供了参考.研究结果表明其在某些频带内具有良好的滤波性能，通过调整等效元件参量(可通过调整单负材料结构参量实现)，可在一定范围内调整该滤波器的中心频率与带宽.这种结构可以使滤波器向微型化、集成化方向发展.

［1］VESELAGO V G.The electrodynamics of substances with simultaneously negative values of ε and μ［J］.Sov Phys Usp，1968，10(14):509－514.

［2］ALÙ A，ENGHETA N.Pairing an epsilon-negative slab with a mu-negative slab:resonance，tunneling and transparency［J］.IEEE Trans Anten Propag，2003，51 (10):2558－2571.

［3］AGRANOVICH V M，GARTSTEIN Y N.Spatial dispersion and negative refraction of light［J］.Physics-Uspekhi，2006，49(10):1029－1044.

［4］JIANG H T，CHEN H，LI H Q，et al.Properties of onedimensional photonic crystals containing single-negative materials［J］.Phys Rev E，2004，69(6):066607－066612.

［5］LI J，ZHOU L，CHAN C T，et al.Photonic band gap from a stack of positive and negative index materials［J］.Phys Rev Letts，2003，90(8):083901(1－4).

［6］CALOZ C，ITOH T.Application of the transmission line theory of left-handed(LH)materials to the realization of a microstrip“LH line”［C］//IEEE Antennas and Propagation Society，AP－S International Symposium (Digest).San Antonio:IEEE，2002:412－415.

［7］CALOZ C，ITOH T.Lossy transmission line metamaterials［J］.Microwave and Optical Technology Letters，2004，43(2):112－114.

［8］POZAR D M.Microwave Engineering［M］.Translated by ZHANG Z，ZHOU L，WU D，et al.3rd Edition.Beijing:Publishing House of Electronics Industry，2006:42－45.