不等长非均匀有损耗传输线FDTD瞬态分析

史凌峰 林 凯 袁 冰 叶 强 赵亚楠

(1.西安电子科技大学超高速电路设计与电磁兼容教育部重点实验室，陕西 西安 710071； 2.西安电子科技大学电路CAD所，陕西 西安 710071；3.陕西广播电视大学，陕西 西安 710068)

1. 引 言

在当今大规模高速集成电路的设计中，信号频率的提高和电路规模的不断增大，使得电路系统内部传输线的耦合问题日趋严重，从而对多导体传输线的瞬态分析成为了研究热点。目前，针对传输线耦合问题的研究多集中在等长均匀传输线的瞬态响应上[1-3]，而对于不等长、非均匀的多导体传输线的研究，多是在忽略传输线损耗的情况下进行的[4-5]，且并没有形成一个比较完善的理论。然而在实际高速电路系统中，连接系统中各信号处理器的传输线通常会出现不等长、非均匀等情况。同时，随着信号频率的提高，传输线损耗对信号完整性的影响越来越大。因此，对不等长非均匀有损耗传输线的研究具有重要的现实意义。

目前，分析多导体传输线的主要方法有数值拉氏反变换法(NILT)[6]、时域有限差分(FDTD)法[3,7]等。数值拉氏反变换法可以单独对取样点上的时域信号进行求解，但误差较难控制[5]。时域有限差分法可以获得传输线上任意点的电压、电流波形，并且结果直观，计算量较小，可以对非线性系统进行分析[5]。

本文基于FDTD法，提出了适用于分析不等长非均匀有损耗多导体传输线的瞬态响应的计算方法，并利用该方法对不等长传输线模型进行了数值计算和理论分析，仿真实验证明了该方法的有效性。

2. 不等长非均匀有损耗传输线的FDTD算法

图1为不等长非均匀多导体传输线模型，其中导体1、导体2为信号线，导体3(未画出)为参考地平面，并在导体1的始端设置激励源。L1为导体1的长度，L2为导体2的长度。由图1可以看出：沿信号传输方向L1距离内，导体1、导体2和参考地平面(未画出)组成了三导体传输线，之后的L2-L1距离内，导体2和参考地平面(未画出)组成了二导体传输线。

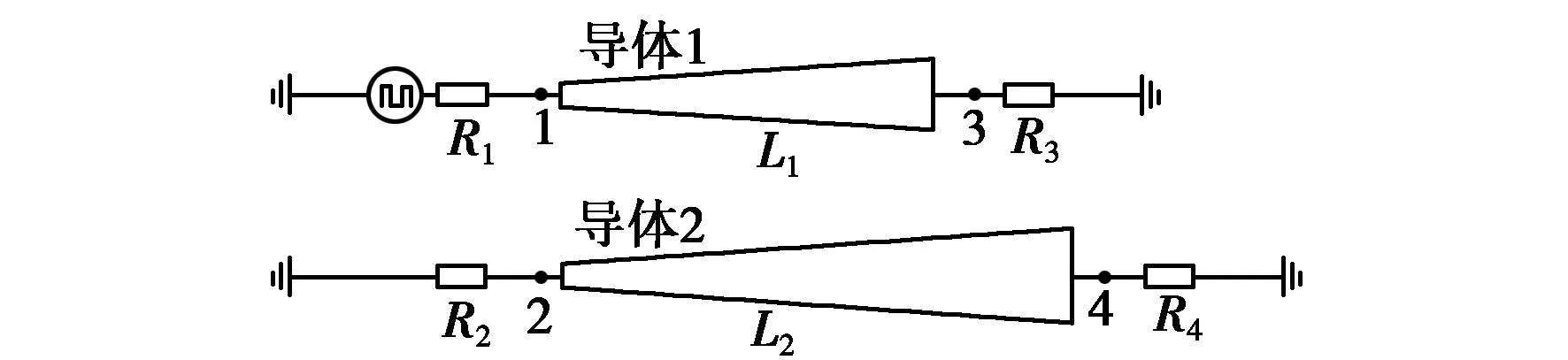
图1 不等长非均匀多导体传输线模型

按照FDTD方法将多导体传输线离散化[7-9]，如图2所示。其中：Vs0为始端端接激励矩阵，Rs0为始端端接电阻矩阵;Rs1为沿信号传输方向L1距离处的端接电阻矩阵;Rs2为终端端接电阻矩阵;图中电压节点与电流节点均相距Δz/2，时间点的间隔为Δt/2。

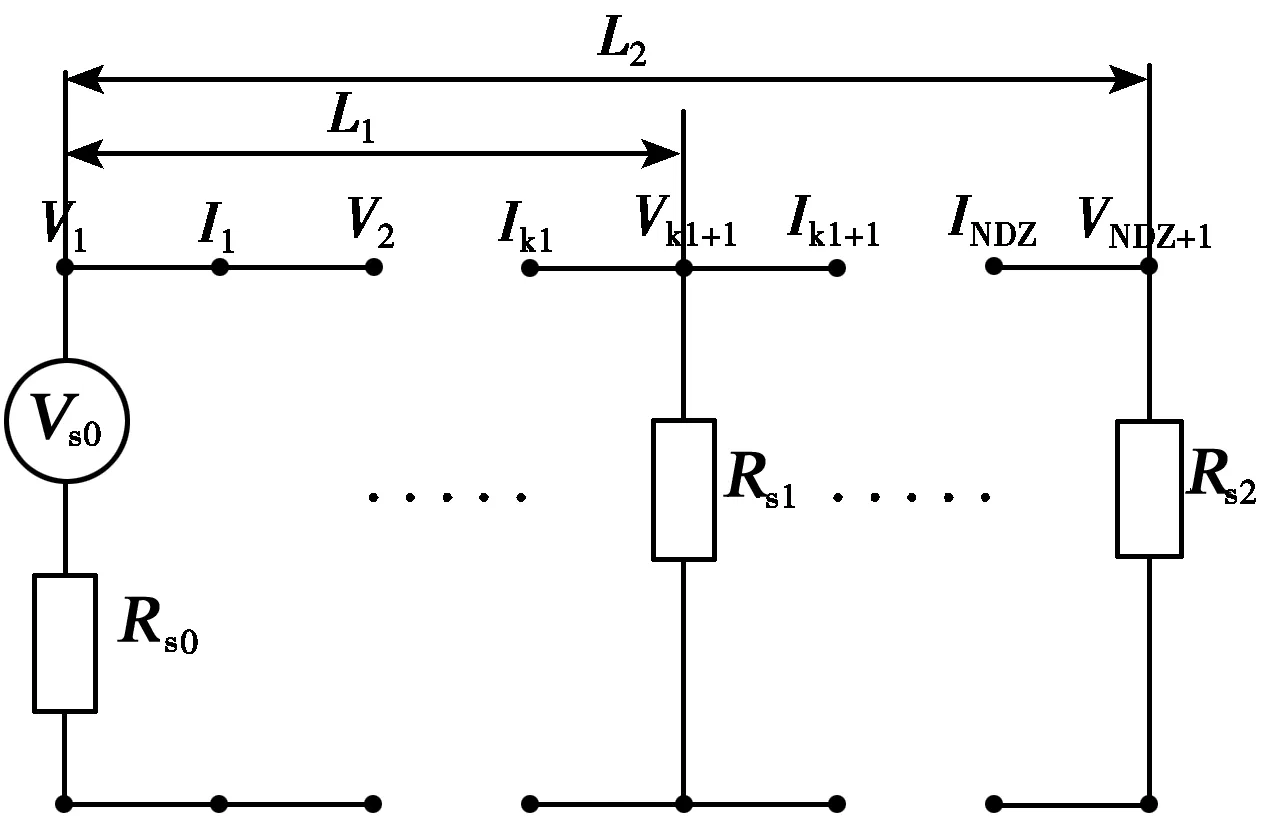
图2 多导体传输线的离散化

根据图2所示，在不考虑外界电磁场作用的情况下，多导体传输线方程的时域形式为

(1)

(2)

式中：V和I分别为多导体传输线上的电压和电流矩阵；R和G分别为多导体传输线上的电阻和电导矩阵；L和C分别为多导体传输线上的电感和电容矩阵。

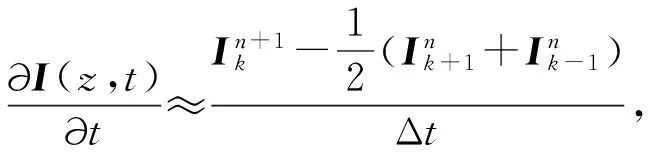
(3)

(4)

式中：E为单位矩阵。

根据传输线始端和终端边界条件，结合式(3)和式(4)可以得到传输线在始端和终端的电压迭代公式

(5)

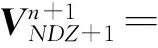
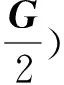
(6)

式中：RS为始端电阻矩阵；RL为终端电阻矩阵。

为计算传输线始端的电流，应用Kirchhoff定律，可以得出其电流的迭代公式[10]

(7)

对于如图1所示的不等长非均匀多导体传输线，在始端以及L1和L2-L1长度范围内的等长多导体传输线处，均满足各自的多导体传输线方程，利用FDTD法对其进行差分，结果即为公式(3)、(4)、(5)、(7)。而在不同段的等长多导体传输线的分段处，电压相等，电流对导体长度的导数相等。因此，在分析不等长多导体传输线时，可以在初始端以及不同的等长多导体传输线段中对其满足的多导体传输线方程进行差分，而在连接处使其满足连接条件[8]。

在两段不同的等长传输线连接处，较短传输线的端接电阻为线路中的实际电阻，而较长传输线与参考地平面为开路，其端接电阻可以看作无穷大。同时，在连接处，较短传输线中只有Δz/2长度起作用，所以与较短传输线相关的电容量与电感量取原来的一半[8]。因此，在计算各段连接处电压时，对于较短传输线使用公式(6)、较长传输线使用公式(3)。而计算连接处电流时，其计算公式与公式(4)相同，只是对于不同的分段及各段连接处代以不同的电感矩阵和电阻矩阵即可。

综上式(3)、(4)、(5)、(6)、(7)为传输线上各点的迭代公式。Δz、Δt分别为空间和时间步长，k，n分别为空间和时间的划分数。为了保证算法稳定，通常要求Δt≤Δz/V，当取等号时，Δt为最佳时间步长。其中V为电磁波在多导体传输线中传播的最大速度[7]。

计算时，交替使用电压递推公式和电流递推公式，对传输线上各点进行迭代，便可以得到不等长非均匀多导体传输线上各点的时域响应。

3. 仿真验证

考虑如图1所示3导体不等长非均匀传输线作为仿真模型。将其按图2的方法进行离散。则1至k1分段为3导体传输线，k1+1至k2分段为2导体传输线。传输线的分布参数为[11-13]：

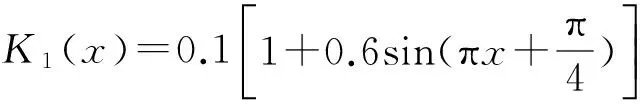
L(x)=387/[1+K1(x)

nH/m

Lm(x)=K1(x)L(x)

nH/m

C(x)=104.13/[1-K2(x)]

pF/m

Cm(x)=-K2(x)C(x)

pF/m

R(x)=30/[1+K3(x)]

Ω/m

G(x)=0.001/[1-K3(x)]

S/m

模型中电磁波在传输线1和传输线2中传播的速度分别为V1=1.521×108m/s，V2=1.482×108m/s.因此，选取V1来确定最佳仿真步长，以保证算法的稳定。在导体1的始端接上升/下降沿为500 ps，脉冲宽度为5 ns，幅值为1 V的激励源，如图3所示。取Δz=0.002 m，根据Δt≤Δz/V，得最佳仿真时间步长为Δt=1.315×10-11s.

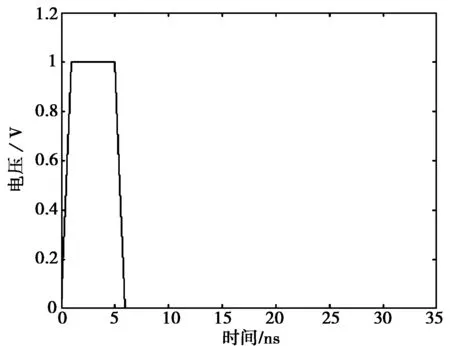
图3 激励波形

对于分段处，以图1形式设置电阻为R1=50 Ω，R2=75 Ω，R3=10 Ω，R4=10 Ω.

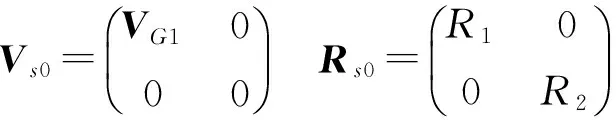
式中：VG1为导体1始端激励电压。

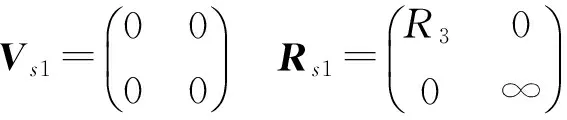
当k=k2+1时，Vs2=(0)Rs2=(R4)

Gs2=(G(k×dz)/2)Cs2=(C(k×Δz)/2)

Ls2=(L(k×Δz)/2)

为验证算法的有效性，取导体1长度为0.1 m、导体2长度为0.104 m.这种情况下，由于两传输线长度相差很小，可以将两传输线近似地认为等长，仿真得到不等长非均匀有损传输线两端各点电压波形，如图4所示。再取导体1、导体2长度为0.1 m，使用文献[13]中提出的等长非均匀有损耗多导体传输线的计算方法(见文献[13]的第29页)，仿真得到传输线两端各点电压波形，如图5所示。比较图4和图5，可以看出：图4中端点4的电压幅值略高于图5中端点4的电压幅值，这是由于图4的仿真模型并不是标准的等长传输线，从而导致了两组仿真试验中受扰线远端串扰的电压幅值有所不同，这一现象与传输线理论是相一致的[14]。除此之外，两者可较好地吻合。由此可得：文中提出的针对不等长有损耗多导体传输线的FDTD算法是可行有效的。

下面分析不等长非均匀多导体传输线的情况，取导体1长度为0.1 m、导体2长度为0.2 m，分别进行两组仿真实验。其中第一组仿真忽略传输线的损耗(R=0，G=0)，第二组仿真考虑传输线的损耗。实验结果分别如图6、图7所示。

将图4与图7进行比较，可以看出：当导体1长度不变，导体2长度变化时，有激励源的导体1两端电压变化不大，而无激励源的导体2两端电压的主要区别为远端串扰的瞬态响应发生时间不同，且由于导体2长度不同，其远端串扰的电压幅值有所下降，同时波形趋于稳定的时间也不同。这与文献[4]所得出的结论一致。

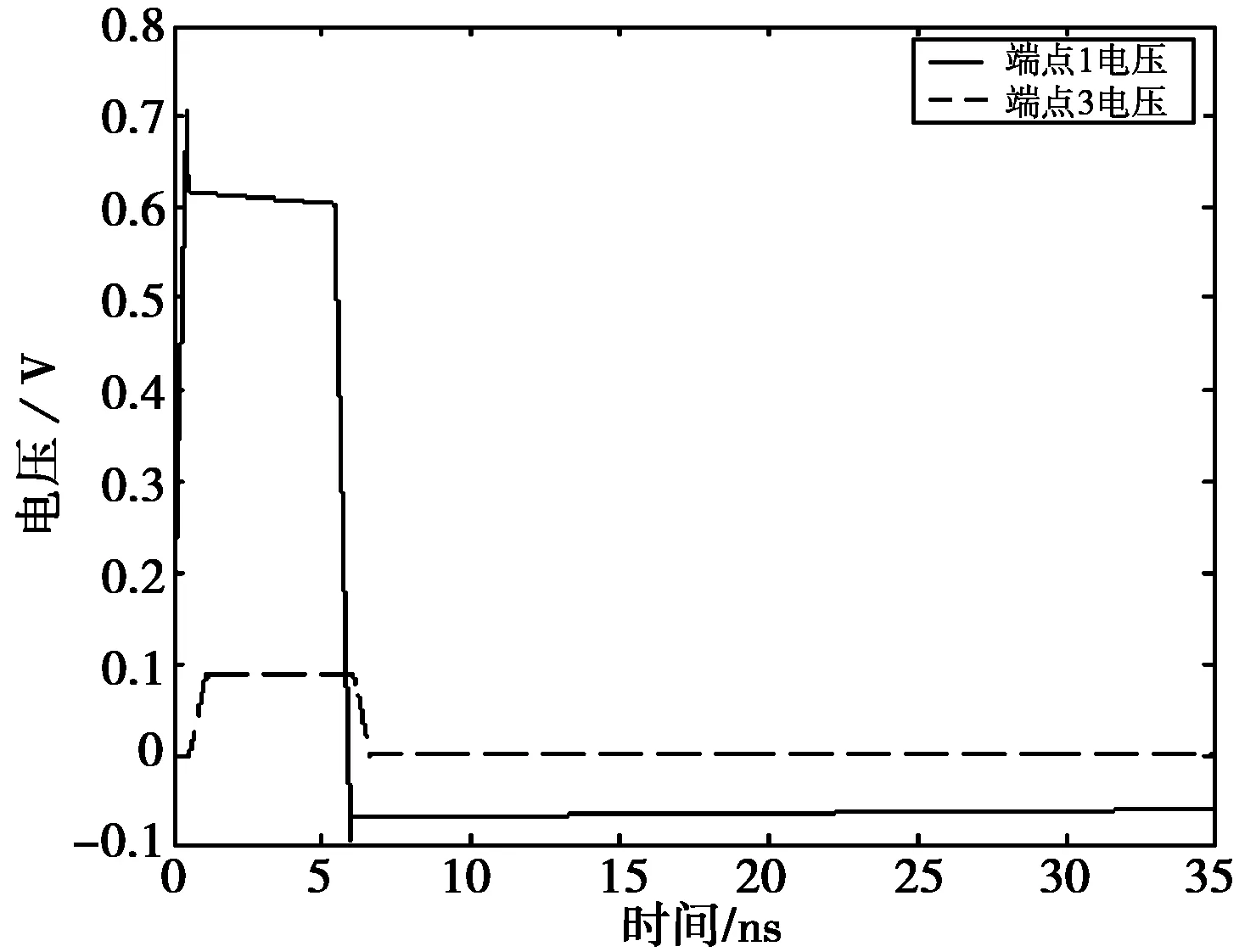
(a) 传输线端点1和3电压波形

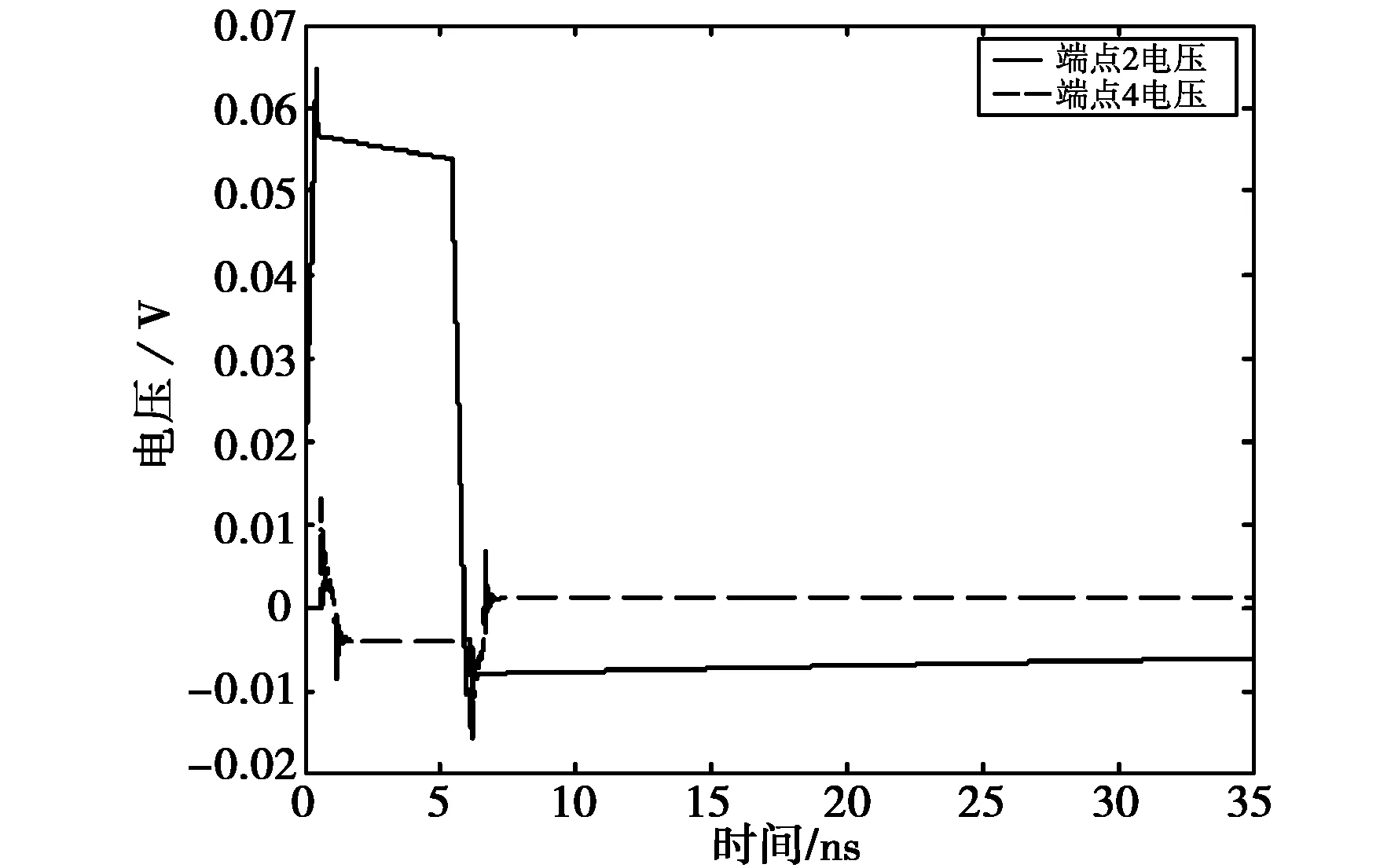
(b) 传输线端点2和4电压波形图4 L1=0.1 m，L2=0.104 m时不等长非均匀有损耗多导体传输线两端电压波形

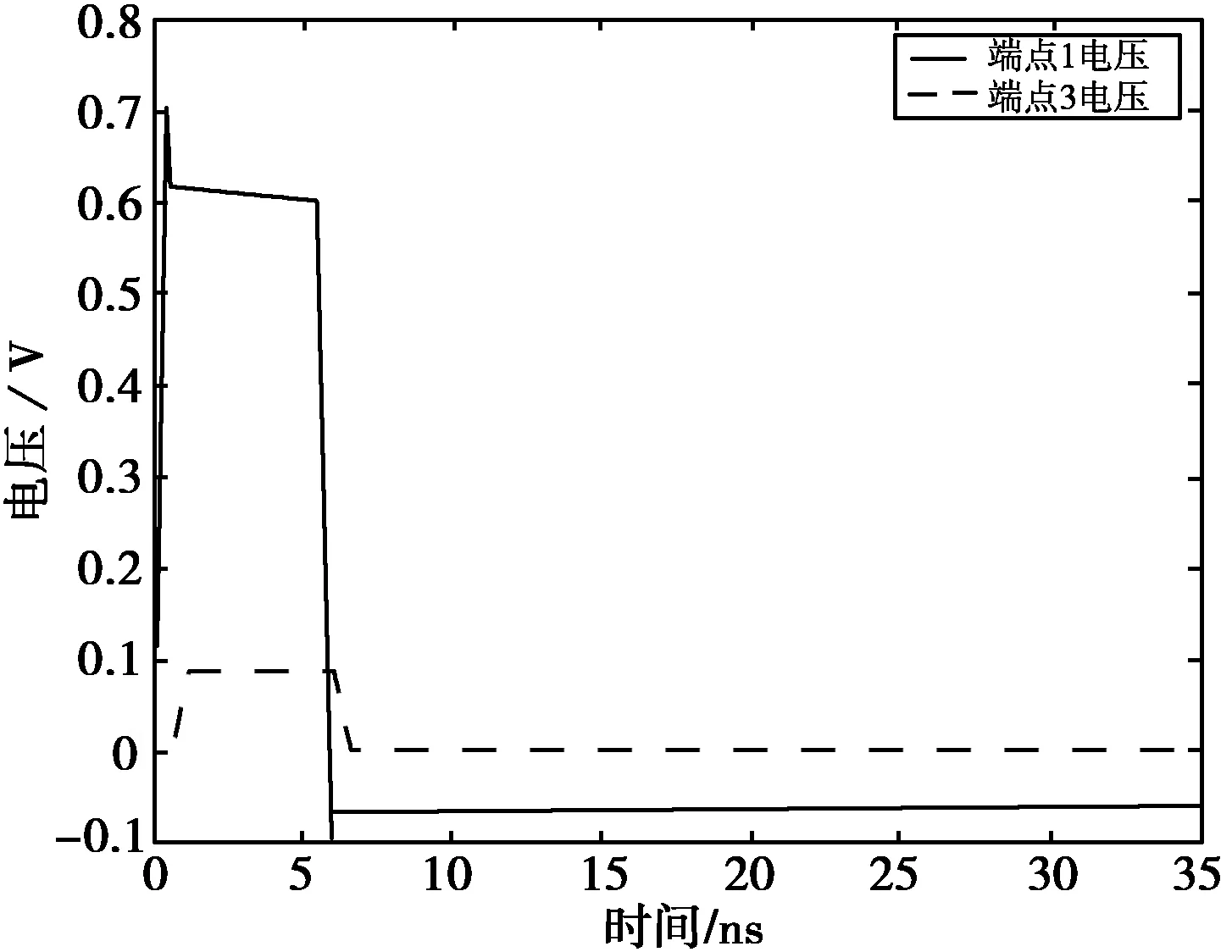
(a) 传输线端点1和3电压波形

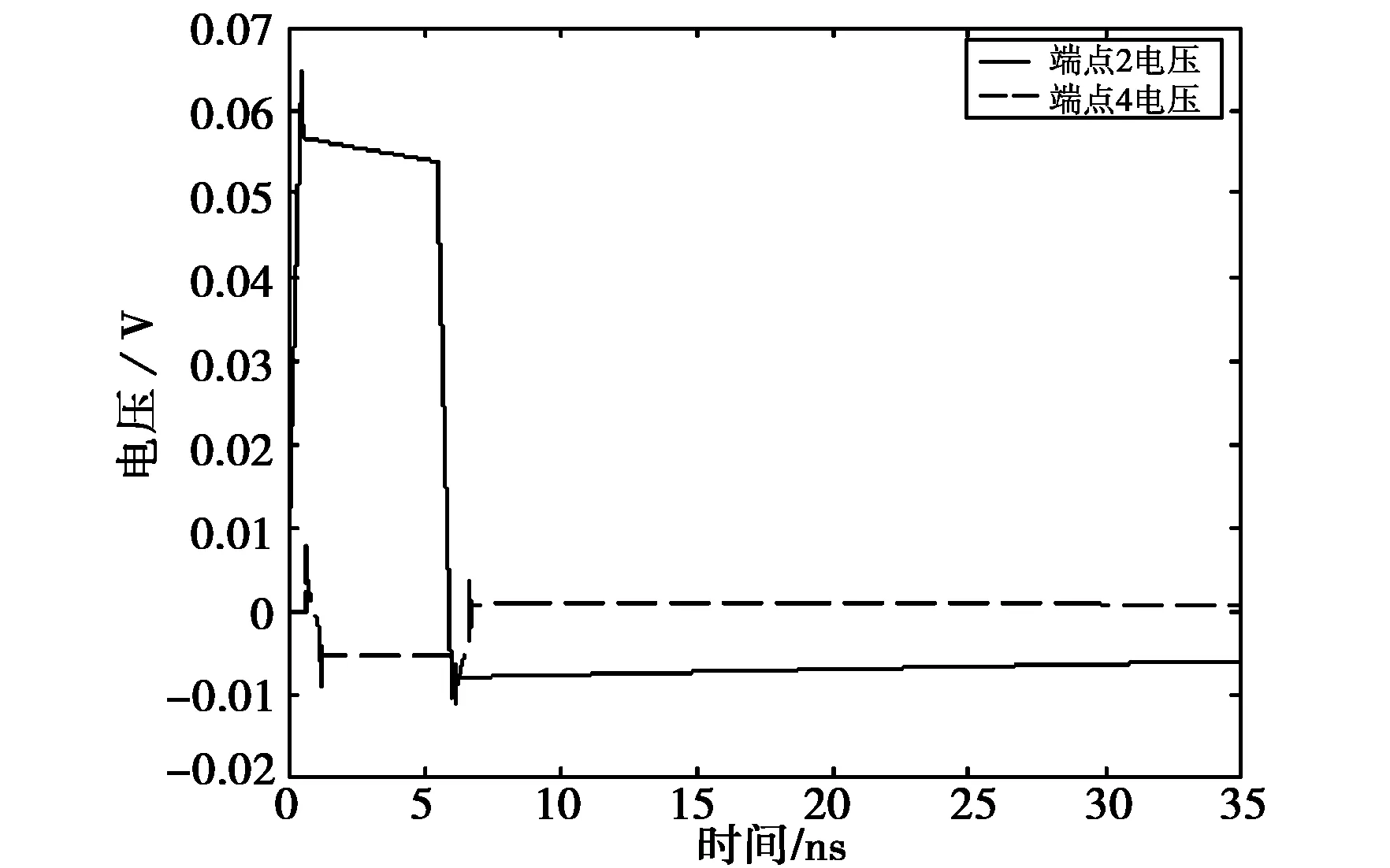
(b) 传输线端点2和4电压波形图5 L=0.1 m时等长非均匀有损耗多导体传输线两端电压波形

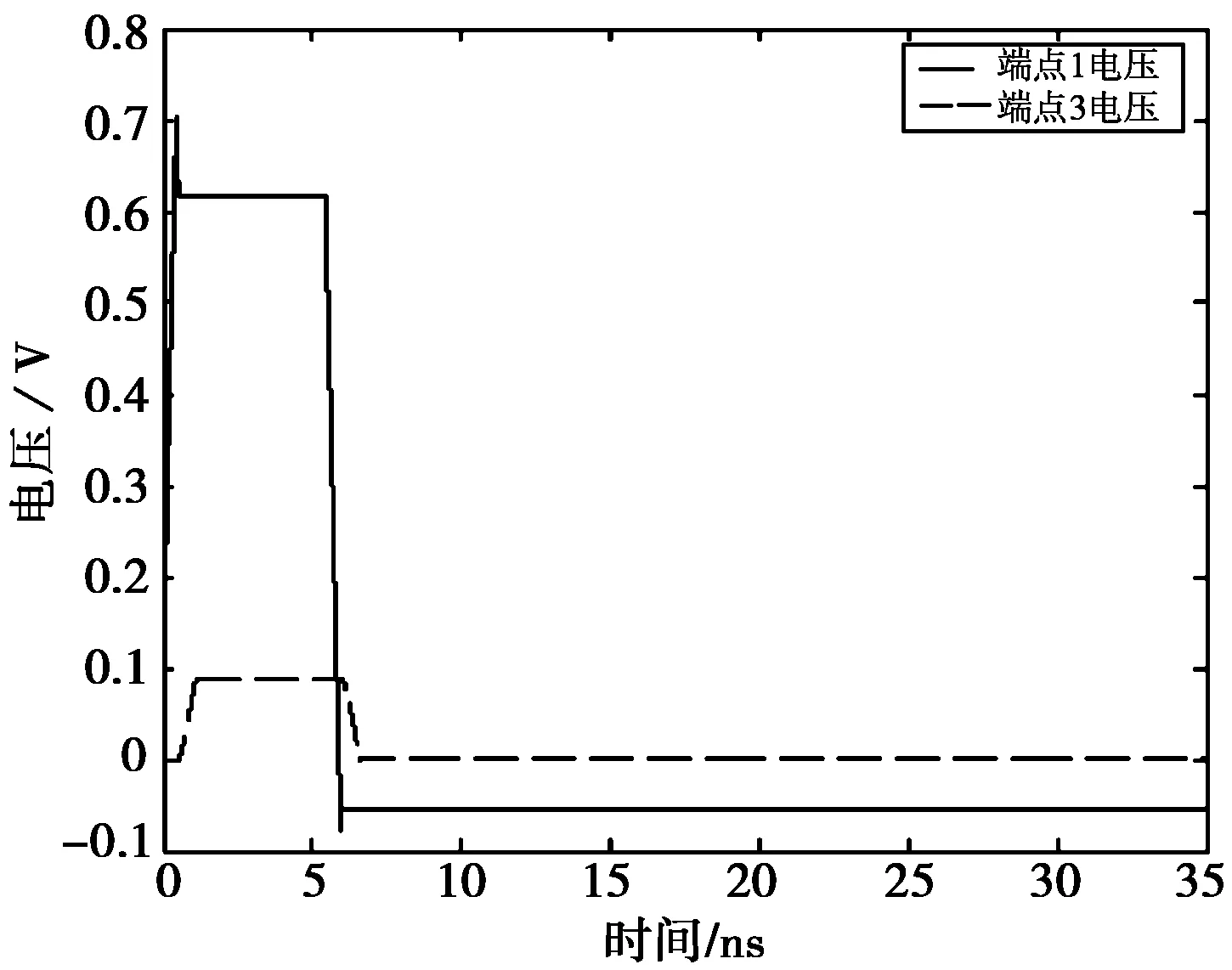
(a) 传输线端点1和3电压波形

(b) 传输线端点2和4电压波形图6 L1=0.1 m，L2=0.2 m时不等长非均匀无损耗多导体传输线两端电压波形

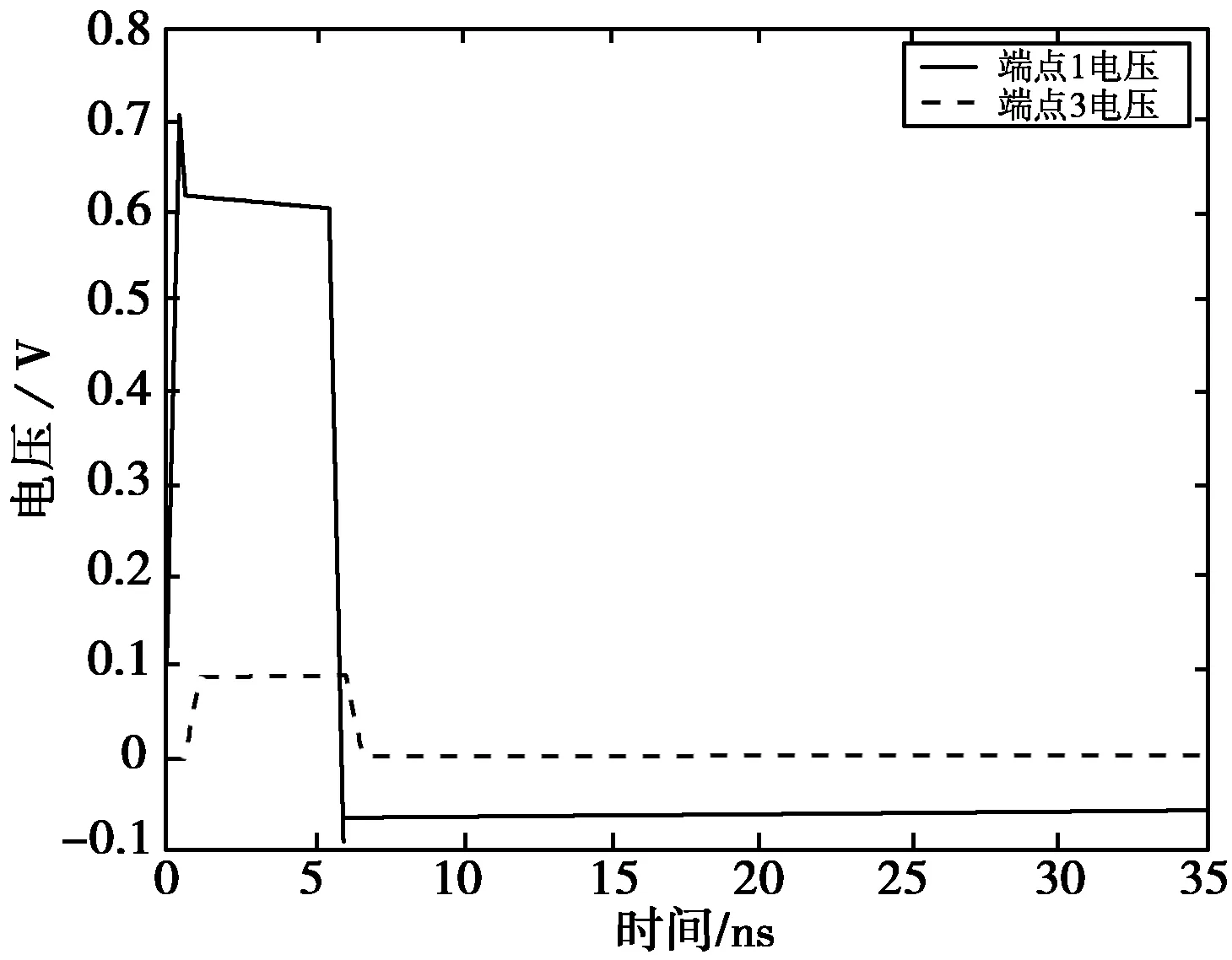
(a) 传输线端点1和3电压波形

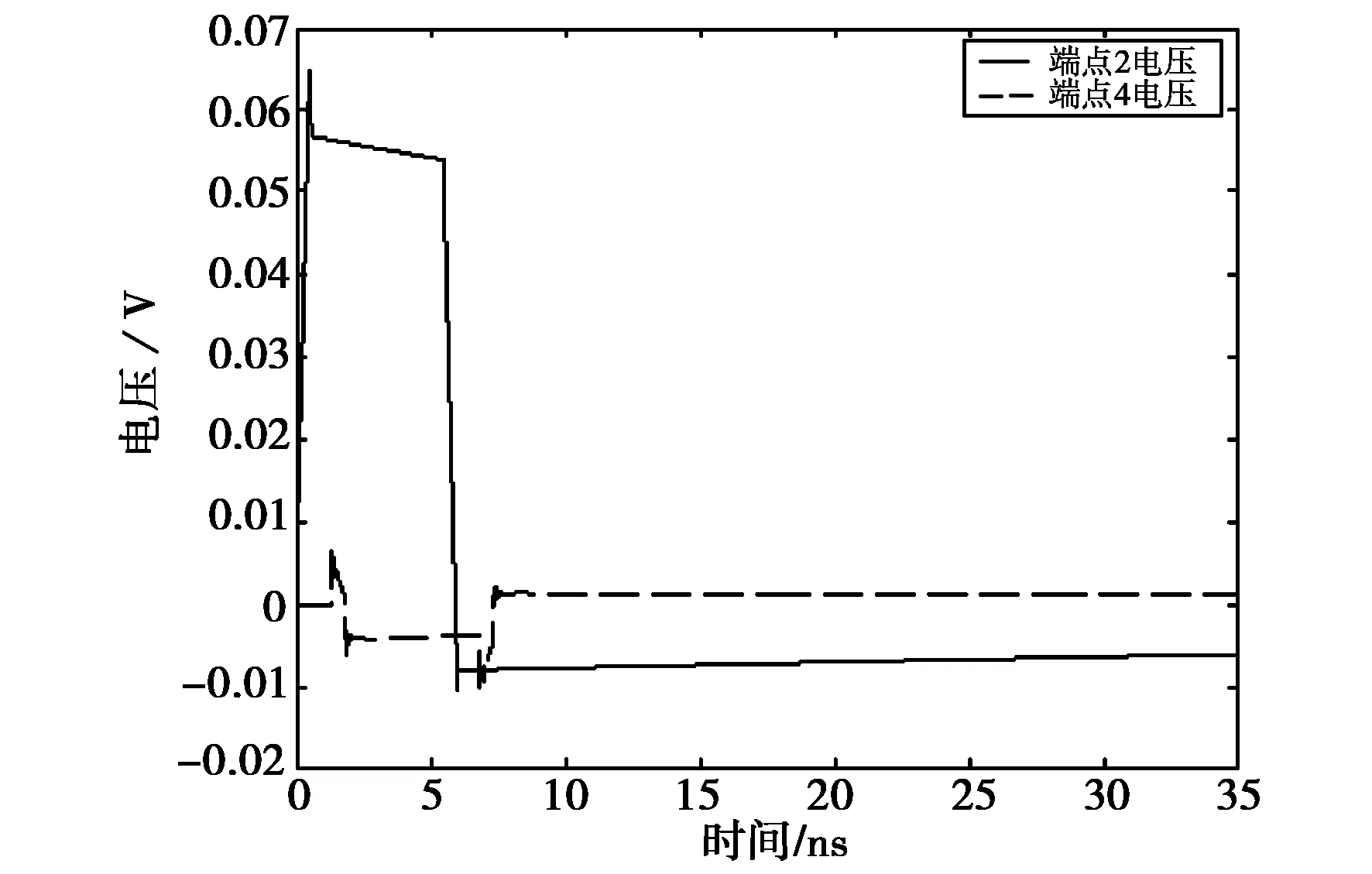
(b) 传输线端点2和4电压波形图7 L1=0.1 m，L2=0.2 m时不等长非均匀有损耗多导体传输线两端电压波形

比较图6与图7，可以看出传输线的损耗导致了导体两端电压有减小的趋势。另外，由于传输线损耗的存在，使得导体1的终端电压幅值、导体2近端串扰与远端串扰的电压幅值均有所下降。这与传输线理论也是相一致的[14]。

4. 结 论

针对传输线损耗以及不等长非均匀多导体传输线之间的耦合是目前大规模高速电路系统的设计难点问题，作者提出了基于FDTD法的不等长非均匀有损耗传输线瞬态响应的算法，并通过实验仿真分析，得出了与参考文献[4]、[14]相一致的结论，证明了该方法在考虑传输线损耗的情况下，可以准确、快速地计算不等长非均匀多导体传输线中各点的瞬态响应。为不等长非均匀有损耗传输线的研究提供理论参考。

[1] YIN Ming, DONG Wenbing. A new method to predict the crosstalk of multiconductor transmission lines[C]// 1997 International Symposium on Electromagnetic Compatibility Proceedings (Cat.No.97TH8218), 1997, 219-222.

[2] ANTONINI G, ORLANDI A, PAUL C R. An improved method of modeling lossy transmission lines in finite-difference, time-domain analysis[C]//IEEE International Symposium on Electromagnetic Compatibility, 1999,1:435-439.

[3] ORLANDI A, PAUL C R. FDTD analysis of lossy, multiconductor transmission lines terminated in arbitrary loads[J]. IEEE Transactions on Electromagnetic Compatibility, 1996, 38(3): 388-399.

[4] 李 莉, 冀维林. 端接非线性负载的不等长传输线瞬态分析[J]. 电波科学学报, 2009, 24(4): 529-532.

LI Li, JI Weilin. Transient analysis of unequal length multiconductor transmission lines loaded by nonlinear devices[J]. Chinese Journal of Radio Science, 2009, 24(4): 529-532. (in Chinese)

[5] 齐 磊, 卢铁兵, 崔 翔. 端接非线性负载的非均匀传输线瞬态分析[J].电波科学学报, 2009, 18(2): 153-156.

QI Lei, LU Tiebing, CUI Xiang. Transient analysis for nonuniform transmission lines with nonlinear loads[J]. Chinese Journal of Radio Science, 2009, 18 (2): 153-156. (in Chinese)

[6] 郭裕顺. 用NILT导出的传输线瞬态分析模型[J]. 电子学报. 2002, 30(3): 381-385.

GUO Yushun. Transmission line model for transient simulation derived using the NILT technique[J]. Acta Electronica Sinica, 2002, 30(3): 381-385. (in Chinese)

[7] CLAYTON R P. Analysis of multiconductor transmission lines[M]. New Jersy: John Wiley & Sons Press. 2008.

[8] 李 莉. 时域有限差分法和多导体传输线理论中若干问题的研究[D]. 北京: 北京邮电大学,1998.

[9] 高本庆. 时域有限差分法[M]. 北京: 国防工业出版社,1995.

[10] 郑生富. 有损均匀传输线的时域有限差分法研究[D]. 重庆: 重庆大学, 2007.

[11] BOULEJFEN N, KOUKI A B, GHANNOUCHI F M. Frequency and time domain analyses of nonuniform lossy coupled transmission lines with linear and nonlinear terminations[J]. IEEE Transactions on Microwave Theory and Techniques, 2000,48(3): 367-379.

[12] XU Qinwei, MAZUMDER P. Accurate modeling of lossy nonuniform transmission lines by using differential quadrature methods[J]. IEEE Transactions on Microwave Theory and Techniques, 2002, 50(10): 2233-2246.

[13] 唐 旻. 高速集成电路频变参数互连线信号响应分析[D]. 上海: 上海交通大学,2007.

[14] BOGATIN E. Signal integrity: Simplified[M]. Beijing: Publishing House of Electronics Industry, 2007: 334-339.