高阶调制LDPC码在水声信道中的仿真分析

李玉祥，梁国龙，张光普，付 进，殷敬伟

(1.哈尔滨工程大学理学院，哈尔滨150001，liyuxiang051111@126.com; 2.哈尔滨工程大学水声技术国防科技重点实验室，哈尔滨150001)

当今的频率资源越来越有限，为了提高频带利用率可以采用具有高阶谱效率的调制方式.正交幅度调制(Quadrature Amplitude Modulation，QAM)通过对相位和振幅的联合控制，在最小距离相同的条件下，QAM星座图中可以容纳更多的星座点，从而可在限定的频带内传输更高速率的数据.因此，以M－QAM为代表的高阶调制技术是一种常用的提高频谱利用率的技术.LDPC［1］编码技术是信道编码领域最受瞩目的研究热点，1/2码率的二元LDPC码在AWGN信道下的性能距信息论中的Shannon限仅差0.004 5 dB，是目前最接近Shannon限的好码［2］.将LDPC码与高阶调制进行结合，能够发挥高阶调制的频谱利用率的优势，又能够利用LDPC码接近Shannon限的特性，提高译码性能，实现有效传输.

1 高阶软解调

LDPC码采用迭代译码方法，是软输入软输出译码.软判决译码与硬判决译码相比，能够提高译码性能，但由于每个高阶调制符号对应着多个比特，计算每个比特对应的软信息是很复杂的.1994年，Goff，S.Le［3］在某种特定的格雷映射方式下，给出了一种计算软比特信息的简化递推公式; 2002年，Tosato，F［4］按照HIPERLAN/2给出的格雷映射关系推导了另一组计算LLR的递推公式.文献［5］在此基础上利用接收点到星座点距离的几何关系提出了简化算法.

1.1 精确的LLR算法

对数似然比(Log-Likelihood Ratio，LLR)是利用接收符号来判断发送比特为0和发送比特为1的概率比值的对数.发送b比特的LLR［6］为

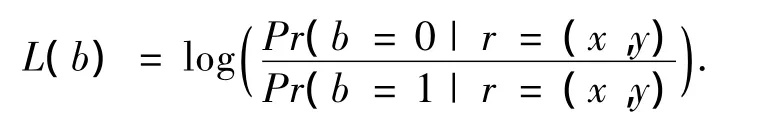
假定所有的符号等概率分布，在AWGN信道条件下的LLR可以表述为

其中:sx，sy表示理想星座点的同相坐标和正交坐标分量;s0，s1表示理想星座点某比特位为0或1的集合.

1.2 近似的LLR算法

近似的LLR算法是考虑接收信号第i比特到最近星座点第i比特的距离，而不用考虑到所有星座点距离的近似算法.它的定义［7］为

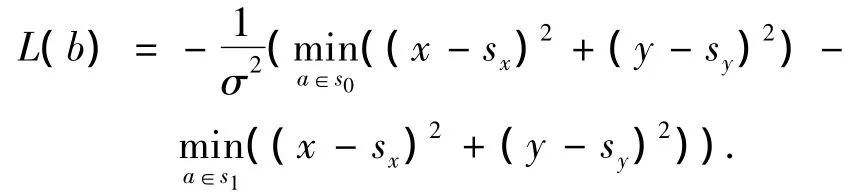
它是利用接收信号点与其相邻星座点的距离特性来判断接收信号的符号.如果L(b)＞0，则判断接收信号r的第i比特为1，L(b)的大小表示其判断为1的可靠性;如果L(b)＜0，则判断接收信号r的第i比特为0，|L(b)|的大小表示其判断为0的可靠性.这个近似算法利用接收信号点与其邻近星座点的距离判断符号，大大减少了运算量.

1.3 简化形式的LLR算法

文献［5］对近似的LLR形式又进行了简化.把对接收信号点与邻近星座点的距离简化成仅计算接收信号点与邻近星座点在水平或垂直方向上的距离，即将二维的距离简化成一维的距离，进一步减少了计算量，且对系统性能的影响较小.其简化的近似LLR为

式中:Di表示接收信号r与判决边界THi的最小欧式距离.其判决边界THi为与接收信号点最近的水平或垂直方向第i比特的0星座点与1星座点的中垂线.

1.4 简化算法的应用

根据对称性，若判决区域在复平面具有左右对称性，则LLR只依赖I路信号绝对值.若判决区域在复平面具有上下对称性，则LLR只依赖Q路信号绝对值.若判决区域THi为常数，则LLR只与实部有关;若判决区域THq为常数，则LLR只与虚部有关.应用这个方法对高阶调制的变量进行LLR判决.以16QAM为例，其星座图如图1所示.下面的二进制序列表示16QAM中与数字0～15对应的格雷码.

图1是16QAM的星座图，根据对称性，可简化至仅对第一象限进行分析.b3简化判决区间和边界是图1的纵轴，复平面左半边部分是b3=0判决区域，右半边部分是b3=1判决区域.可得b3位软信息是LLR3=yi.

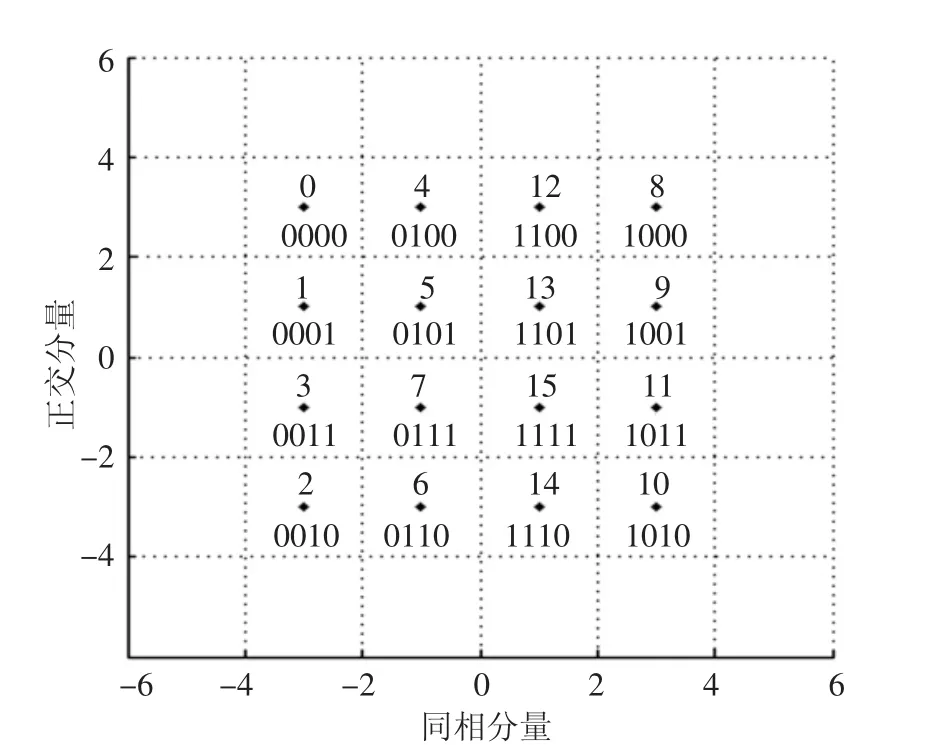
图116 QAM星座图

图2是b2简化判决区间和边界.在判决边界左边b2=1，在判决边界右边b2=0.可得b2位软信息是LLR2=2－|yi|.

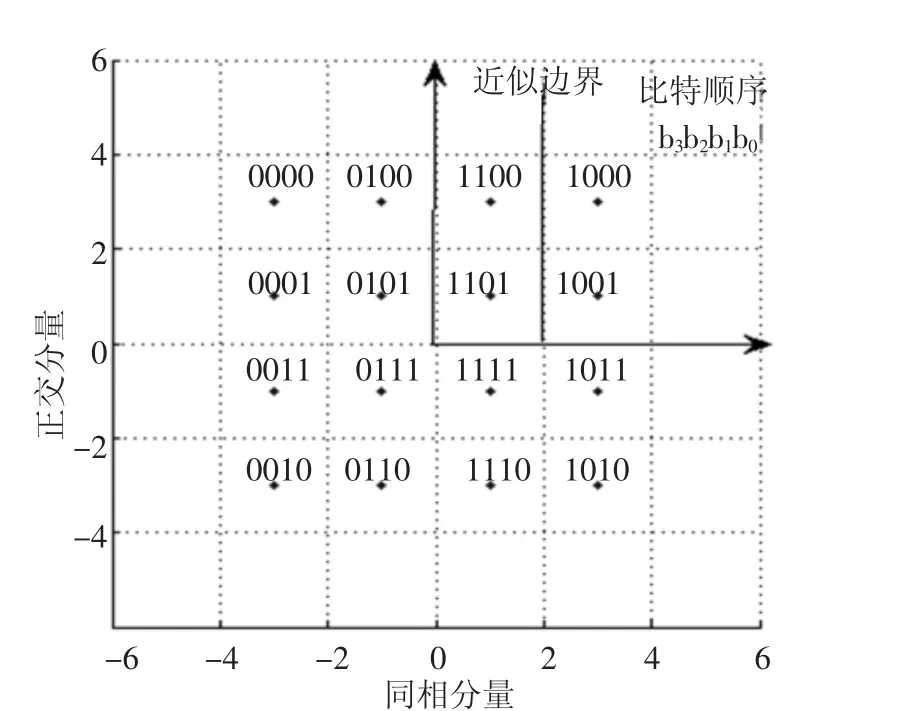
图2 b2简化判决区间

b1简化判决区间和边界是图1的横轴.在复平面上半边部分b1=0，在复平面下半边部分b1=1.可得b1位软信息是LLR1=－yq.

图3是b0简化判决区间和边界.在判决边界上边b0=0，在判决边界下边b0=1.可得b0位软信息是LLR0=2－|yq|.

最终得到对于16QAM各比特的对数似然比为LLR3=yi，LLR2=2－|yi|，LLR1=－yq，LLR0= 2－|yq|.按照同样的方法可得到 32QAM、64QAM、128QAM的软输入对数似然比.

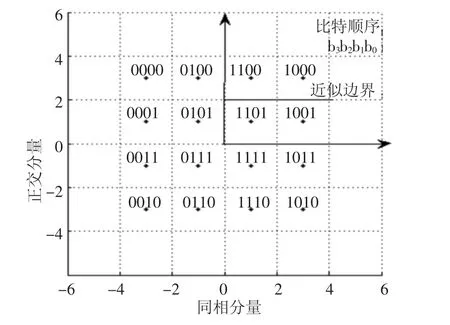
图3 b0简化判决区间

2 高阶调制LDPC码水声通信系统

2.1 系统构成

高阶调制LDPC码水声通信系统的构成如图4所示.信源为所要传输的信息数据，经过LDPC编码，在本系统中采用随机构造的校验矩阵，用基于近似下三角矩阵的编码方式.然后经过MQAM方式调制，经过信道传输.接收端计算高阶调制软输入信息，采用LLR BP译码方式，最终到达信宿.

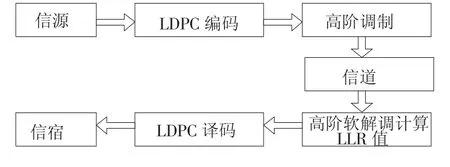
图4 高阶调制LDPC码水声通信系统

2.2 LDPC码性能仿真

2.2.1 信道仿真.在对LDPC码应用在水下无线通信中的性能仿真之前，先要对水下信道特性［8］进行仿真，仿真条件如下:发射换能器距水面40 m，接收换能器距水面40 m，传输距离2 000 m，声速为1 500 m/s.得到水下信道的冲激响应如图5所示，信道的最大延迟时间0.142 s，多途路径数为25.

2.2.2 性能曲线及分析.仿真条件:用随机构造方法构造一个240×480的校验矩阵，码率为1/2，列重为3，行重为6的规则LDPC码，此校验矩阵的密度为0.03.信息传输速率为1 Kbit/s，用LLR BP译码方法进行译码，迭代次数为20次，100帧数据，得到LDPC编码的16QAM与无编码的16QAM调制的性能曲线如图6所示.结果表明，随着信噪比的增加，16QAM-LDPC系统的误码率降低，要明显好于无编码的16QAM系统，实现了较好的传输性能.

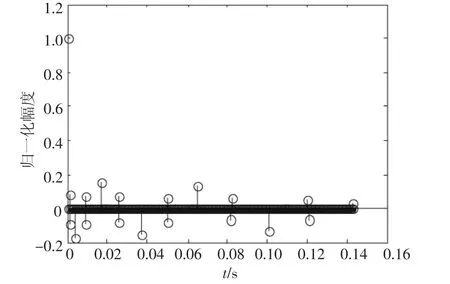
图5 水下信道的冲激响应

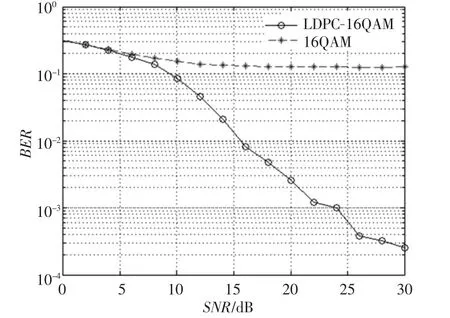
图6 性能仿真曲线

2.2.3 码长对性能的影响.在图7中仿真了码长分别为480，960，2 000的16QAM-LDPC性能曲线.结果表明，在低信噪比区域，随着码长的增加，系统误码率变化不明显，因为低信噪比对高阶调制的符号接收影响较大;随着信噪比的增加，高阶调制对数似然比更加准确，其误码率下降较快，即在高信噪比时增加码长可以改善系统的性能.

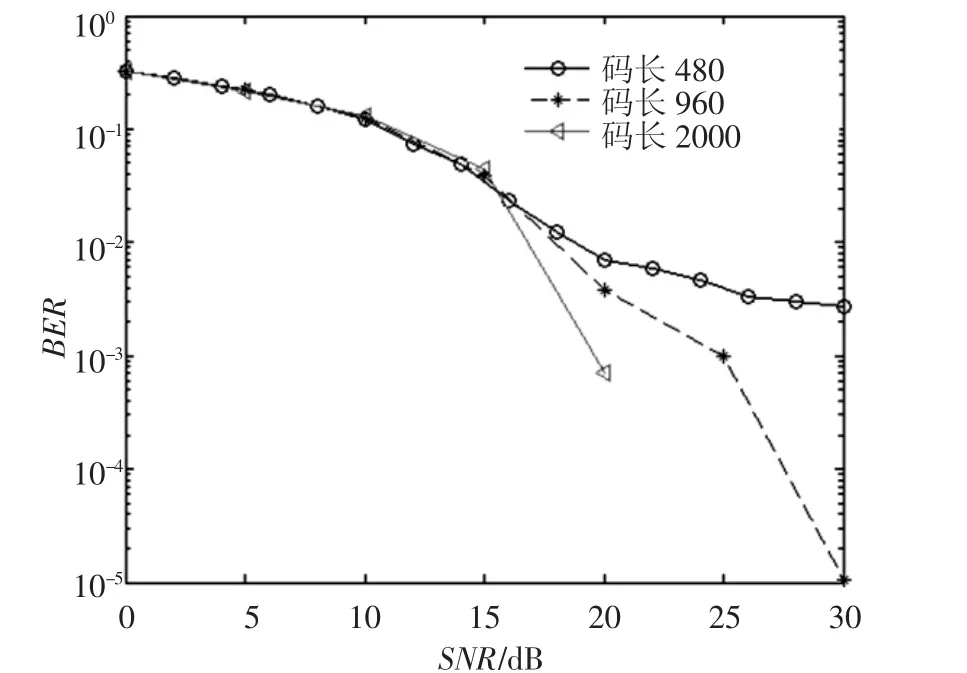
图7 码长不同的性能比较

2.2.4 迭代次数对性能的影响.在图8中仿真了100帧码长为480，迭代分别为5，20，30次时的16QAM-LDPC性能曲线.结果表明，在信噪比较低时，信道条件对高阶调制软信息的判定影响较大，因此增加迭代次数对系统性能提高不大，在高信噪比时，多次迭代能较好的改善系统性能.对于本系统，迭代在20次以上能获得较好的译码性能.

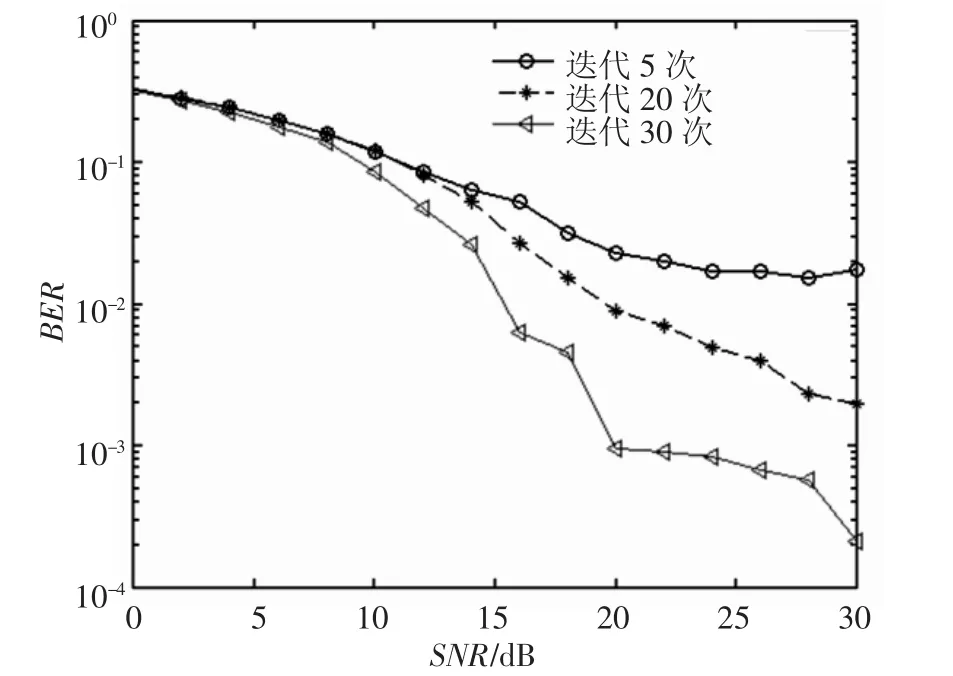
图8 迭代次数不同的性能比较

3 结论

对高阶调制的软信息提取以及影响LDPC码性能的相关因素进行分析，表明高阶调制LDPC码系统适用于高信噪比条件，在信噪比较低时应该采用低阶的调制方式.为了充分研究高阶LDPC码在水下通信中的应用，还应该对更复杂的信道情况，如声速的正梯度分布，负梯度分布以及LDPC码在不同信道条件下的构造等问题进行建模仿真.本文的初步研究表明了高阶调制LDPC码应用在水下无线通信中是可行的，为进一步的研究提供了基础.

［1］GALLAGER R G.Low-Density Parity-Check Codes［R］.Cambridge:MIT Press，1963.

［2］CHUNG S Y，FORNEY J G D，RICHARDSON T J，et al.On the design of low－density parity-check codes within 0.0045dB of the Shannon limit［J］.IEEE Communications Letters，2001，5(2):58－60.

［3］LE G S，GLAVIEUX A，BERROU C.Turbo-codes and high spectral efficiency modulation［C］//Proc IEEE International Conference on Communication.New Orleans，La，USA:［s.n.］，1994，5:645－649.

［4］TOSATO F，BISAGLIA P.Simplified soft－output demapper for binary interleaved COFDM with application to HIPERLAN/2［C］//IEEE International Conference on Commun.Padova，Italy:［s.n.］，2002，5: 664－668.

［5］王晓晴，杨知行，彭克武，等.一种M-QAM软判决解映射的简化算法研究［J］.电视技术，2008，32 (01):17－19.

［6］VITERBI A J.An Intuitive Justification and a Simplified Implementation of the MAP Decoder for Convolutional Codes［J］.IEEE Journal on Selected Areas in Communications，1998，16(2):260－264.

［7］Mathworks.Communications Toolbox［EB/OL］.http://www.mathworks.com/access/helpdesk/help/ toolbox/comm/ug/bqwswmc－1.html.

［8］惠俊英，生雪莉.水下声信道［M］.第2版.北京:国防工业出版社，2007.