敏捷制造中面向盟友选择问题的遗传算法

朱 伟，徐克林，朱 易

(同济大学机械工程学院，上海201804，zhwliuhui@163.com)

随着全球经济一体化、网络化的进程，敏捷制造(Agile Manufacturing，AM)理念应运而生，敏捷制造中具有代表性的组织形式虚拟企业(Virtual Enterprise，VE)，即核心企业通过招投标的形式联合本地或异地的相关优势互补资源，为及时响应市场机遇而结成的动态联盟成为全球学术界和企业界关注的焦点［1］.

盟友选择是结成动态联盟的核心环节，它其实是一个多目标组合优化问题［2］.随着问题规模的不断扩大，传统的运筹学方法及启发式算法在盟友选择问题上的应用受到限制，如文献［3－4］提出了重复启发式算法，算法有效但通用性不强.遗传算法(Genetic Algorithm，GA)受启于自然界优胜劣汰的自然法则，将问题的求解过程表达为染色体的选择、交叉和变异等遗传操作，通过全局搜索求得问题的最优解或满意解.文献［5］提出了以代码串表达基因的编码方式，因代码串长度与候选资源的数量相关，故而易引发解空间爆炸膨胀问题.文献［6］提出的遗传算法编码简单，但遗传算子操作复杂，而且容易产生非问题解.

本文设计了面向敏捷制造盟友选择问题的遗传算法.算法采用字母与数字混合编码，直观、简单且遗传操作均在解空间进行，因而不会产生非法解.实验结果表明，算法在解的质量和稳定性方面有良好性能.

1 盟友选择问题建模

1.1 问题描述

盟友选择问题可以描述为:核心企业根据实际情况将制造任务分解为多个单元任务，把自己无优势或无能力完成的单元任务放于网上投标，搜索参与竞标的所有候选资源并对竞标者考核选择:首先根据实力、信誉、质量、价格、交货情况和时空等指标进行定性分析，选择出可用资源;然后以最优化某指标为手段，选择出完成任务的最满意资源组合［7］.本文以成本最低为优化目标.

1.2 模型假设

1)各制造单元任务内容无重复;

2)一单元任务能且只能被一资源投中;

3)一资源有且仅有一次投标机会;

4)某些单元任务间有制造联结约束;

5)若单元任务i和j存在制造联结，则其相应竞标资源间有物流联结费用发生.

1.3 模型建立

1.4 符号说明

T=(t1，t2，…，tn)为单元任务的编码向量，B=(b1，b2，…，bm)为可用资源的编码向量，D= {(i，j)|i∈(1，2，…，n－1)，j∈(2，3，…，n)}为存在制造联结的两任务集合表示任务 i的投标向量，x'i为 xi的转置向量，表示资源 k的投标向量，xk'为xk的转置向量，c表示资源k对单元任务i的投标价格.

2 面向盟友选择问题的遗传算法

2.1 个体编码

采用字母和数字混合编码方案，设单元任务i的投标资源数为m，将单元任务i和投标资源的对应关系依次编码为Ti1，Ti2，…，Tim.用单元任务对应染色体的基因，设单元任务数为n，则问题空间可表达为一组编码长度为n的染色体(g1，g2，…，gn)，其中，gi∈(Ti1，Ti2，…，Tim)，(i=1，2，…，n).染色体结构意义为:资源b1中标单元任务1，资源b2中标单元任务2，依此类推，资源bn中标单元任务n，基因的位置序列即相应的任务序列.

2.2 初始种群的产生

步骤1 随机产生n个Ti1～Tim之间的编码作为染色体基因的值，生成一条长度为n的染色体.

步骤2 重复步骤1，直到生成的染色体数目满足群体规模.

2.3 适应度函数［8］

在遗传算法中个体的适应度越大越好，而盟友选择问题是目标函数越小越好，所以需要将目标函数f(x)变换为个体的适应度函数F(x).所采用的变换如下:

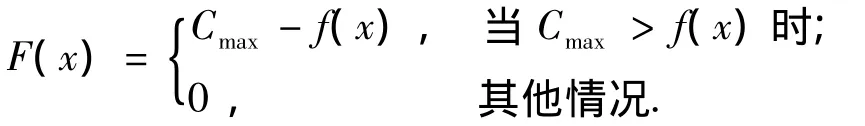
其中:Cmax为足够大的实数且最好与群体无关，这里选取Cmax等于最大适应度值.

2.4 遗传操作

2.4.1 选择操作

选择操作采用基于排序的选择方法，首先对种群个体适应度值排序，按设定比率淘汰低适应度值个体，剩余个体(最优个体除外)按轮盘赌方法参与选择.

2.4.2 交叉操作

为避免产生非法个体，交叉操作限制在等位基因之间进行.选取两父代体A和B，随机产生两个表示交叉点的自然数，不妨取n1=3，n2=7，互换两点外等位段基因的值，形成表达问题的子代体A1和B1.子代体A1、B1的结构形成过程如下:

采用等位分段交叉算子，可以满足资源和单元任务间的约束关系，保证了新个体的合法性.

2.4.3 变异操作

为避免产生表达非法解的个体，算法设计了如下的变异算子:任务号不变，资源号加1，用任务号和资源号的新对应关系编码取代原编码而形成新基因.下面以父代染色体C为例说明变异操作过程:取其两基因T42和T73，分别用T43和T74取代它们而形成新个体C1，其结构如下:

变异操作中，资源号采用循环取值.

2.5 面向盟友选择问题的遗传算法［9］

综合以上讨论，结合局部搜索算法，下面给出求解面向盟友选择问题的遗传算法.

输入可用资源投标价格表、各制造联接资源物流费用表、淘汰率Pe、种群规模Popsize，最大进化代数M、交叉概率Pc、变异概率Pm;

输出最优选择方案;

Begin

染色体编码，根据单元任务规模产生N个初始个体，组成初始种群P(T);

代数T:=0;

利用局部搜索算法对初始种群改进，并评估最终得到的初始种群，如满足设定的终止条件，则输出最优选择方案并退出算法;否则，执行以下步骤;

T代最优个体复制到T+1代;

用轮盘赌方法从T代中选择父体，按交叉概率Pc操作产生交叉子体，按变异概率Pm操作产生变异子体;

交叉子体和变异子体加入T+1代种群P(T+1);

利用局部搜索算法对新种群改进，并评估最终得到的新种群，如满足设定的终止条件，则输出最优方案并退出算法;否则执行以下步骤;

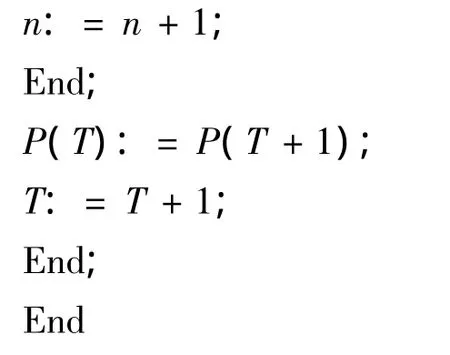
3 算例及分析

3.1 算例

本文以文献［1］案例作为验证算例.某核心企业有一大型制造任务，需选择合作伙伴共同完成.该企业对此任务进行了分解，经过招投标和初步选择考核，确定了完成各个单元任务的可用资源，现欲以制造成本最低为优化目标来确定最佳制造资源组合.

图1为资源联结图，图中bij表示任务i的第j个投标者，箭头方向表示制造任务联结的投标资源之间的物流发生方向.表1为各资源对相应单元任务的投标价格，表2～5为制造联结资源之间发生的物流费用.

图1 资源联接图

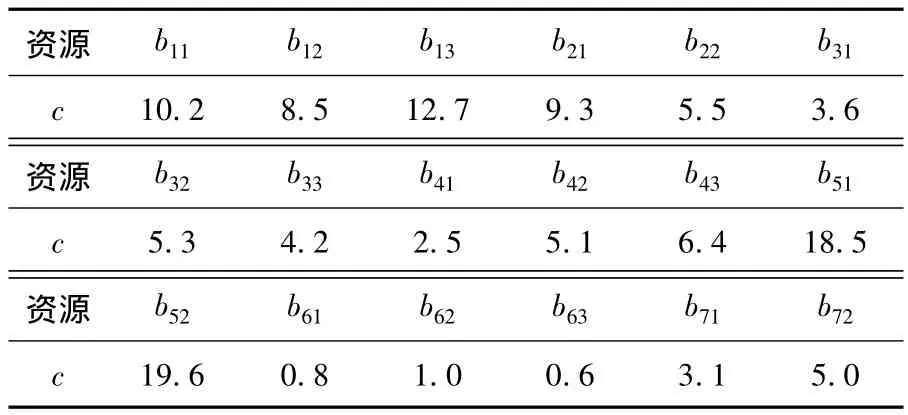
表1 各资源投标价格c 万元

表2 资源b1、b4至b5的物流费用f14－5 万元

表3 资源b2、b3至b4的物流费用f23－4 万元

表4 资源b5至b6的物流费用f5－6 万元

表5 资源b6至b7的物流费用f6－7 万元

3.2 结果及分析

算例中，单元任务数为7，因此，染色体长度为7.取淘汰率Pe=0.2、种群规模为40、交叉概率Pc=0.7、变异概率Pm=0.2、进化代数为80.

在Dell Inspiron1420 PC机、Windows XP环境下运行算法50次，其中44次得到问题最优解，其染色体结构为:T12T22T33T41T51T63T71，表示资源组合R12、R22、R33、R41、R51、R63和R71为最优，对应的总成本为45.5万元;6次得到问题次优解，其染色体结构为:T12T22T31T41T51T63T71，表示资源组合R12、R22、R31、R41、R51、R63和R71为次优，对应的总成本为45.6万元.所得结论和文献［1］一致，证明了算法的可行性和可靠性.

4 结论与展望

1)讨论了面向敏捷制造动态盟友选择的遗传算法，算法采用字母与数字混合编码方式，在等位基因间进行交叉与变异操作，克服了传统遗传算法操作复杂且易产生非法解等缺点.

2)算法寻优效果明显，稳定性强.

3)下一步拟研究约束条件的智能自适应，以增强算法的鲁棒性和可进化性［10］，以便操作复杂大型的制造任务和动态盟友选择问题.

［1］张洁，高亮，李培根.多Agent技术在先进制造中的应用［M］.北京:科学出版社，2004.

［2］李灵能，罗中先，戴跃洪.敏捷制造平台上动态联盟盟友的选择［J］.机械设计与制造，2007(6):194－196.

［3］伍乃骐，苏平.敏捷制造下合作伙伴选择的有效算法［J］.计算机集成制造系统，2004，10(8):971－979.

［4］WU Nai-qi，MAO Ning，QIAN Yan-ming.An approach to partner selection in agile manufacturing［J］.Journal of Intelligent Manufacturing，1999(10):519－529.

［5］冯蔚东，陈剑，赵均纯.基于遗传算法的动态联盟伙伴选择过程及优化模型［J］.清华大学学报:自然科学版，2000，40(10):120－124.

［6］郭怀瑞.敏捷制造系统的重构算法［D］.武汉:华中科技大学图书馆，2000.

［7］张翠军，贺毅朝，王金山.敏捷制造中制造资源选择问题的遗传算法［J］.计算机工程与应用，2007，43 (10):217－218.

［8］王凌.智能优化算法及其应用［M］.北京:清华大学出版社，2001:154－159.

［9］柳林.基于遗传算法的 Job－Shop调度问题求解［J］.计算机应用，2006(7):1695－1696.

［10］WU C G，XING X L，LEE H P，et al.Genetic algorithm application on the job shop scheduling problem［C］//Proceedings of 2004 International Conference on Machine Learning and Cybernetics.Shanghai，China:［s.n.］，2004:2102－2l06.