混沌键控数字保密通信研究新进展

丁 群,王佳楠

(黑龙江大学 电子工程学院,黑龙江 哈尔滨 150080)

0 引 言

混沌键控通信方式是一种用于传输数字信号的调制方式,与前两种通信方式相比,混沌键控抗噪声和参数失配的能力较强,克服了混沌遮掩通信方式中要求混沌载波功率远大于有用信号功率的缺点[7]。混沌键控以其较强的抗干扰能力、较好的发展前景与实际应用价值,使其在数字保密通信中具有非常重要的研究价值。一种通信系统想要很好的应用于实际当中,关键是要有高速的数据传输速率并且存在信道噪声和畸变时要有好的误码率特性,同时要适应现代通信的需要具有较高的保密性和频带利用率[8]。与基于传统的同步的调制方法相比,混沌键控数字保密通信调制方法在信道中更具优越性。

本文着重综述了近年来混沌键控数字保密通信系统技术的主要进展,包括理论、设计思想、目前的研究热点、可能实现的又有一定实用价值的几种保密通信方案,以及各种方案的优缺点和应用研究概况,包括在该领域所取得的研究成果,提出了一种新型的CD-DCSK(相关延迟-差分混沌键控)混沌键控保密通信系统,最后,对今后混沌保密通信技术的问题作了概括,提出一些看法和值得研究的方向。

1 几种典型的混沌键控保密通信系统

混沌键控通信系统的接收端,按照检测方式的不同,可以分为相干解调和非相干解调两种类型。相干解调系统需要在接收端准确地复制出用于携带信息的混沌载波,而非相干解调系统则并不需要。相干解调系统一般需要使用同步来复制出混沌载波,而非相干解调可以有多种形式,但它们的基本原理都是利用发射的混沌信号本身所具有的一些特性。这些特性可以是一些内在的确定性特征 (例如,自相关性、基于回归映射的检测和最大似然方法等),或者通过恰当地安排发射参考信号和信息信号到达接收端的时间顺序,例如,DCSK(差分混沌键控)、CDSK(相关延迟键控)和QCSK (四相正交混沌相移键控)等[9]。

1.1 CSK(混沌移位键控)数字通信系统

CSK调制方式的基本原理是将不同的二进制数据映射到不同的混沌基函数上,再将调制后的混沌信号作为载波发送出去,在接收端,按照相应的接收原理以一定的方法从混沌信号中恢复出二进制数据。当发送端使用一个混沌信号发生器时,可以将CSK调制分为正反极性CSK和COOK(混沌开关键控);当发送端采用两个混沌信号发生器时,根据接收端采用的检测方式,可以分为相干解调和非相干解调两种类型。

相干解调需要在收发两端建立起一个混沌同步系统,它不仅具有保密性,而且其抗噪声性能优于非相干解调。但是,当传输信道的信噪比较低时,相干解调的混沌同步难以建立,杂波会破坏同步过程,容易造成误码;其次,混沌系统达到同步状态需要一定的时间段,因此最大数据传输速率不高,此时宜用非相干解调。非相干解调不具有保密性,通过观察一些传输信号的统计数量进行辨析,结果就有可能恢复加密的二进制信息,但其方法简便,易于实现,电路简单。所以在实际应用中,非相干解调相对于相干解调要更加实用,还有很大的发展空间。在保持良好同步的条件下,相干解调的CSK其噪声性能要优于COOK,而COOK的抗噪声性能要优于非相干解调的CSK系统[10]。同时, CSK系统信号的解调是基于比特能量的估计,因此检测器的阈值应当随着噪声水平的变化而变化,否则就会产生很多误码,所以CSK系统在实际应用上还存在很大的局限性。

1.2 DCSK和FM-DCSK数字通信系统

DCSK是一种采用非相干解调的调制方式,在DCSK调制方式中,每个信息符号的周期划分为两个相等的时隙。第一个时隙用于传输混沌参考信号,而第二个时隙则用来传送携带信息的信号。当发送的数字信号为 “+1”时,发射信号就是参考信号本身;当发送的数字信号为“-1”时,发射的是反向的参考信号。DCSK的调制和解调的框图见图1,Tb为一个符号周期的时间,在第l个符号周期内,DCSK发送端的输出信号s(t)为:

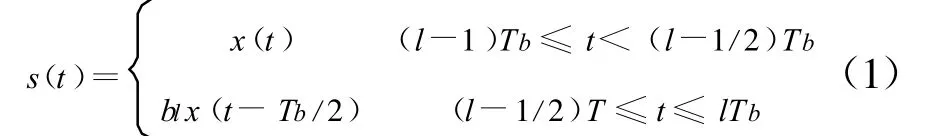
式中x(t)为混沌序列;bl是值为±1的数字信号。在接收端,将符号周期后半段接收到的与前半段接收到的信号进行相关计算,即可以解调出发送的有用信号;r(t)表示发射信号s(t)经过噪声信道,混有噪声信号。

图1 DCSK系统解调电路框图Fig.1 Flowchart of the DCSK system

由于现有的DCSK非相干解调只区分信息信号和参考信号的同相和反相,所以其保密性较低,在信道中传输的信号被截获后很容易被破译[11-12],而且在一个符号周期内,仅有一半时间用于传输携带信息的信号,而另一半时间则只是用来传输参考信号,降低了带宽利用率。接收端的相关运算结果与每一比特时间长度Tb有关,如何提高数据传输速率,同时希望运算结果稳定,减少误码率,是信号传输的关键。

C组(12.458±0.882)MPa，3种不同表面处理方式的抗剪切强度均达到临床要求，但差异具有统计学意义(P<0.05)。

由于混沌信号具有非周期的特性,DCDK调制方式使得单位比特能量随着时间而改变,从而造成了接收端出现估计问题。随后为解决这一问题提出了FM-DCSK(调频差分混沌键控)。FMDCSK调制器的结构与DCSK调制大体相同,只是其混沌基函数是经过FM调制后的混沌波形。因为混沌调频信号的幅度是恒定的,FM-DCSK信号中所有比特的能量都维持不变,所以FM-DCSK比DCSK具有更良好的性能[13]。但是由于基函数中的参考信号和信息承载信号的关系未变,因此FM-DCSK的解调过程与DCSK的相同,这就使得FM-DCSK和DCSK一样存在数据传输速率不高和系统保密性低等缺点。

1.3 CDSK数字通信系统

为了提高带宽利用率和连续发射信号,Sushchik等提出了CDSK(相关延迟键控)方式[14]。CDSK调制方式克服了DCSK的不足,发送端的开关用加法器取而代之,使发送端可以连续工作,而且也不会有信号的重复发送,使系统的安全性得到提高。在发射端,延迟后的混沌信号经待发送的信息调制后,加到原来的混沌信号中构成发射信号s(t)。在第l个符号周期内,发射信号s(t)为:

其中τ表示延迟时间。

在接收端,一个基于相关器的接收机用于还原发送的信号。CDSK采用的是非相干调制通信方式,发送端将参考信号与携带信息的延迟信号相加,然后一并发射出去,使系统的数据在信道中传输的安全性得到保证,但是系统的性能要比DCSK略有不足[15-16],而且CDSK传输信号的每比特能量仍然不恒定,不能满足高速传输的要求,所以其传输性能还有待提高。

1.4 QCSK数字通信系统

QCSK是在非相关DCSK系统的基础上提出的调制方案,QCSK系统在一个符号周期内,也分为参考信号与数据信号两部分,它在信道中不需要传送正交信号,并且使单个符号所代表的信息变为2比特,得到双倍的频谱利用率。选择两组经过归一化处理的正交混沌基信号cx(t)和cy(t),且在半个符号周期内满足:

QCSK调制解调的原理框图见图2,信号a,b是传输信号K通过串并转换后得到的有用信号, QCSK调制就是利用两个互相正交的混沌基函数在一个码元时间内传输两比特的信息,比DCSK提高了一倍的传输速率。

类似于DCSK调制,QCSK调制也是在前半个符号比特内发送混沌参考信号,后半个符号周期内用于传输承载消息信号的已调混沌参考信号。发送端发送的调制的信号可表示为式 (4),其中Eb表示每个传输符号的能量:

图2 QCSK调制解调框图Fig.2 Flowchart of the QCSK system

QCSK与DCSK相比,具有相同的带宽,近似的BER性质[17-18],但更高的数据传输速率,可看作是混沌键控通信发展的一大亮点,为后继的研究工作提供了很多思路。如果将QCSK应用于实际中,还存在许多问题:QCSK系统可以看成是2个DCSK系统的组合,QCSK用系统的复杂性换取了双倍的数据速率[19-20]。在占用相同带宽的情况下,虽然利用2个正交混沌函数的生成,可以提高数据传输速率,但是和DCSK类似,透过观察传输信号的频谱,很容易得知系统的比特率,所以其保密性也和DCSK一样差。并且QCSK系统在实际硬件电路的实现上要用到2个Hibert变换,所以系统要复杂的多,在实际电路应用中很难实现。

2 一种新型的CD-DCSK数字通信系统

考虑到现有混沌键控系统存在的这些问题,我们提出了一种新型的混沌键控系统:CD-DCSK (相关延迟-差分混沌键控)。它的调制解调原理框图见图3,改进后的CD-DCSK在前后1/2符号周期内,分别将2位有用信号a、b调制到发送信息内,得到了双倍的频谱利用率。a、b两位信号可以分别选取“+1+1,-1+1,+1-1,-1-1”4种情况。在调制器端,前1/2符号周期内,发送的信号s(t)a是混沌信号x(t)和延迟τ/2后并经a信号调制后的混沌信号x(t-τ/2)的叠加;在后1/2符号周期内,延迟τ后的混沌信号经b信号调制后,加到原来的混沌信号中构成发射端输出的信号s(t)b。可以看出在信道中传输是均匀的,没有重复的信号,保密性较DCSK得到提高,CDDCSK发送端的输出信号s(t)可以表示为下式:

在前半段和后半段符号周期,信道中传输的都是混沌信号与延迟后并经发送符号调制后的叠加信号,所以在信道中,信号传输的保密性得到了保证。同时在和DCSK相同的符号周期内,两个半段符号周期都有携带有用信号,提高了频带的利用率,数据传输速率是DCSK的2倍。

图3 CD-DCSK通信调制系统框图Fig.3 Flowchart of the CD-DCSK system

在接收端,经过相关器的相关运算,在第l个符号周期内,输出信号Za和Zb可表示成下式:

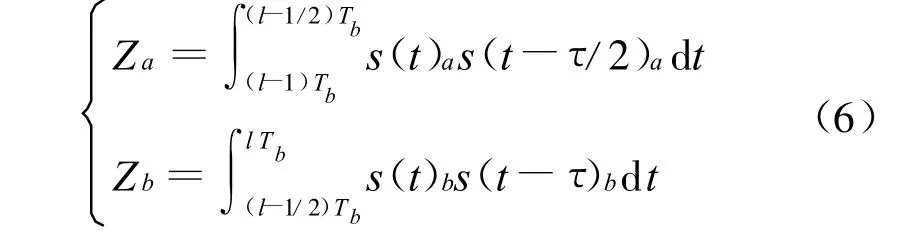
在无噪声环境中,输出信号为:

由Za和Zb表达式可以看出,第一项为有用信号项,第二、三、四项为相邻混沌信号的相关积,由混沌所特有的随机性可以知道,除了第一项有用信号,其余项的积分值均为零。将判决门限设定为零,因为x2(t-τ/2)＞0,x2(t-τ)＞0,所以当Za或Zb＞0时,则可以判断发送的信号a或b为 “+1”;当Za或Zb＜0时,则可以判断发送的信号a或b为“-1”,然后通过并/串转换,即可以恢复原信号。

当信道中存在噪声时,r(t)表示发射信号s(t)经过噪声信道,混有噪声信号ζ(t),此时,相关器的输出Za和Zb分别为:

在AWGN信道中,比较CD-DCSK系统和码元传输速率相等的QCSK系统的误码率性能见图4。M为半个符号周期内所产生的混沌样值的个数。

图4 改进的CD-DCSK系统和QCSK系统误码率性能比较Fig.4 Comparison of BER performance of the improved CD-DCSK system and QCSK

通过分析CD-DCSK和QCSK系统误码率曲线可以知道,系统性能主要受限于参数 M,降低M可以降低误码率,但是这样也就会限制信号的传输速率。从图4可以看出,在AWGN信道下,当信噪比比较低时,CD-DCSK和QCSK的误码率性能比较接近;在Eb/N0＞8 dB条件下,CDDCSK系统误码率性能要远远好于QCSK系统,并且随着Eb/N0的增大,QCSK的误码率相对于CD-DCSK逐渐增大;在给定BER=10-3条件下, CD-DCSK较QCSK调制方式的信噪比提高了2.2～2.7 dB。所以总体上看,CD-DCSK系统的误码率性能要优于QCSK系统。通过分析可以看出CD-DCSK结合了CDSK和DCSK共有的优点,在数据传输的保密性和误码率性能上都有所提高,数据传输速率更是提高到了DCSK的2倍。而且在硬件电路的实现上,CD-DCSK较QCSK简单得多。

3 结 论

近年来混沌通信的研究逐渐向经典通信领域靠拢,提出了许多新的混沌键控调制方法。将混沌通信理论尽快融入到现有的通信理论的研究中,应用到现有的实际通信系统里,充分发挥混沌保密通信的优势,成为混沌通信理论研究的一个重要方向。如今基于混沌同步性能的相干解调还不能满足实际通信中的中、低信噪比要求,因此非相干解调的混沌键控通信技术是目前最有希望进入实用化阶段的混沌通信方式。目前混沌键控通信系统研究的主要方向是,注重与实际应用关系密切的关键技术研究,如保密性能,实际信道中高数据速率状态下的误码率,多用户能力,抗多路传播以及频带和功率的利用率问题。本文提出了一种新型的CD-DCSK(相关延迟-差分混沌键控)混沌键控保密通信系统,通过分析可以看出CD-DCSK结合了CDSK和DCSK共有的优点,在数据传输的保密性和误码率性能上都有所提高,数据传输速率更是提高到了DCSK的2倍,而且利于电路实现。通过不断地研究和发展,混沌键控数字通信技术必将在通信理论和工程应用中发挥重要作用。

[1]Xinlei An,Jianning Yu,Jiangang Zhang,et al.A New M ultistage Chaos Synchronized System for Secure Communications[C]//Fifth International Conference on Natural Computation.2009:437-441.

[2]高金峰,廖旎焕,梁占红.一种超混沌混合保密通信方案[J].电路与系统学报,2005,10(4):128-130.

[3]He Si-Yuan.The Research of Synchronization Communication Technology Based on Chaotic Masking[C]// IEEE International Conference on Intelligent Computing and Intelligent Systems.2009:267-270.

[4]纪 飚,陆佶人.基于混沌参数调制的数字通信方式[J].通信学报,1999,20(11):50-54.

[5]Alvarez G.,Montoya F.,Romera M.,et al.Breaking Two Secure Communication Systems Based on Chaotic Masking[J].IEEE Transactions on Circuits and Systems II:Express Briefs,2004,51(10):505-506.

[6]于 娜,丁 群,陈 红.异结构系统混沌同步及其在保密通信中的应用 [J].通信学报,2007,28 (10):73-77.

[7]Ji Yao,Anthony J.Lawrance.Performance Analysis and Optimization of M ulti-user Differential Chaos-shift Keying Communication Systems[J].IEEE Transaction on Circuits and Systems I:Regular Papers,2006,53 (9):2 075-2 091.

[8]LI H,SI F F.UWB DCSK System Design and Simulation[C]//IEEE International Conference on Test and M easurement,2009:311-314.

[9]李 辉.混沌数字通信[M].北京:清华大学出版社, 2006:35-46.

[10]W.M.Tam,Francis C.M.Lau,Chi K.Tse.Analysis of Bit Error Rates for Multiple Access CSK and DCSK Communication Systems[J].IEEE Transaction on Circuits and Systems I:Fundamental Theory and Applications.2003,50(5):702-707.

[11]韩建群,朱义胜.一种提高调频差分混沌移相键控调制传输效率方法 [J].电子学报,2005,33(6): 1 032-1 035.

[12]MIN X,XU W,WANG L,et al.Promising Performance of a Frequency-modulated Differential Chaos Shift Keying Ultra-wideband System Under Indoor Environments[J].IET Communications,2010,4(2):125-134

[13]Shaoyuan Chen,Lin Wang,Guanrong Chen.Data-Aided Timing Synchronization for FM-DCSK UWB Communication Systems[J].IEEE Transactions on Industrial Electronics.2010,57(5):1 538-1 545.

[14]SUSHCHIK M,TSIM RING L S,VOKKOVSKII A R.Performance Analysis of Correlation-based Communication Schemes Utilizing Chaos[J].IEEE Transactions on Circuits and Systems Part I,2000,47(12): 1 684-1 691.

[15]葛志平,蒋铃鸽,何 晨.一种改进的差分混沌键控通信方案及其性能分析 [J].上海交通大学学报, 2004,38(Z1):14-17.

[16]TAM W M,LAU F C M,TSE C K.Generalized Correlation-delay-shift-keying Scheme for Noncoherent Chaos-based Communication Systems[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2006,53(3):712-721.

[17]GALIAS Z,MAGGIO G M.Quadrature Chaos-shift Keying:Theory and Performance Analysis[J].IEEE Transactions on Circuits and Systems I:Fundamental Theoryand Applications.2001,48(12):1 510-1 519.

[18]LAU F C M,YE M,TSE C K,et al.Anti-jamming Performance of Chaotic Digital Communication Systems[J].IEEE T ransactions on Circuits and Systems I:Fundamental Theory and Applications,2002,49 (10):1 486-1 494.

[19]王光义.混沌数字通信研究新进展[J].计算机工程与应用,2003,39(21):28-30.

[20]WREN T J,YANG T C.Orthogonal Chaotic Vector Shift Keying in Digital Communications[J].IET Communications,2010,4(6):739-753.