无线传感器网络中一种躲避障碍物的地理路由算法

李金宝,郭晓行,张守娟

(1.黑龙江大学 a.计算机科学技术学院;b.物理科学与技术学院,哈尔滨 150080;2.黑龙江省数据库与并行计算重点实验室,哈尔滨 150080)

0 引 言

地理路由因其简单易用而被广泛地应用在无线传感器网络中。地理路由中每个节点需要确定其位置坐标,该坐标分为真实坐标和虚拟坐标两类。真实坐标一般需要通过定位设备(如GPS)来确定,而定位设备存在着价格昂贵、不能在室内操作以及容易出现测量错误等缺点。然而,采用基于跳数建立虚拟坐标的方法不需要额外的硬件支持,而且能够较好地反映节点间的相对位置以及相通性。

在真实的传感器网络中,常常会存在形状不规则的障碍物,这使得数据包转发到障碍物附近时容易产生 “死端”节点。当出现 “死端”节点时,无论是基于真实坐标还是虚拟坐标的地理路由,通常只能通过局部洪泛或FACE[1]算法来解决死端节点问题,但上述方法耗费能量较多,而且会增加路径长度及丢包率。因此,文献 [2]、文献 [3]提出了基于虚拟坐标的地理路由算法,这些算法能够有效地躲避障碍物,避免遇到障碍物附近的 “死端”节点,但增加了路径长度。为了在不增加路径长度的同时解决 “死端”节点问题,可以沿着障碍物的凸点建立路径。根据计算几何学[4],该路径是最短路径。

针对存在障碍物的网络,本文提出了一种躲避障碍物的分布式地理路由算法 (A Geographic Routing for avoiding obstacles,GRdo)。在使用该算法前的网络初始阶段,本文首先提出一种建立虚拟坐标的方法,并引入可见图 (简称CS图),该图辅助路由阶段以最短的路径绕开障碍物。在以上准备工作的基础上,GRdo采用沿着障碍物凸点建立路径的策略,不仅可以避免障碍物附近的 “死端”节点问题,而且可以得到较短的路径。理论分析与实验结果表明:本文提出的路由算法以较短的路径绕开障碍物,有效地完成路由选择过程,降低数据丢包率。

1 相关工作

在对传感器网络地理路由协议的研究中,一些研究人员提出了支持地理路由协议的虚拟坐标建立方法。文献 [5]选择3个边界节点作为信标节点,每个节点根据到信标节点的跳数建立虚拟坐标,该方法所确定的坐标并不唯一,这可能导致路由的失败;文献 [6]选择更多的节点作为信标,这提高了算法的正确性,但是却增加了空间开销;文献[7]提出了一种建立唯一坐标的方法,从而保证了传输的可靠性。在上述路由协议中,都没有考虑障碍物问题。

针对存在障碍物的网络,文献 [8]将网络划分成多个子区域,源节点将数据包从当前子区域发送到目的节点所在的子区域。由于子区域形状不规则,在子区域内仍然存在障碍物,这将导致 “死端”节点的出现从而降低算法性能;文献[2]将网络划分成多个凸形状的子区域,由于子区域内无障碍物而避免了 “死端”节点的产生,但是划分区域的算法比较复杂,需要大量的洪泛信息;文献[3]针对形状规则的障碍物,建立中轴图(MAG)作为路由的向导,每个节点需要计算和存储反映全局拓扑特征的MAG,但由于MAG信息量较大,增加了存储空间的开销;文献 [2]、文献 [3]提出的路由算法虽然可以有效地绕开障碍物,但是却增加了平均路径长度。

2 网络初始化

本文基于以下假设:①网络环境中存在着形状复杂的障碍物,并且障碍物的面积较大;②不存在障碍物互相包围的情况。

2.1 预备知识

网络初始时有N个节点,每个节点p有一个唯一的ID,表示为ID(p);障碍物所形成的“空白区”称做 “面”,每个面对应着一个唯一的标识号,记为FID;边界节点是面边界上的节点,内角＜(＞)180°的边界节点称为凸点(凹点)。应用文献 [9]提出的算法,可以确定边界节点,每个边界节点记录所在面的FID。应用文献[2]中的算法可以确定面的凸点及凹点。对于任意节点p和q,若p到q的最短路径不经过任何凸点,那么q和p是可见的,p是q的一个可见点。如图1,s对于凸点5是可见的,但s对于凸点q是不可见的,因为最短路径是经过凸点1的折线。

定义1:凸面。凸面是面对应的最小凸多边形区域。如图1,face2本身就是凸面,而face1对应的凸面是由凸点 {1,q,2,3,4,5}围成的凸多边形区域。构成凸面的凸点称为顶点。

定义2:CS图。整个网络构建成一个CS图= (V,E),其中V是顶点集合,E是可见顶点对间建立的最短路径集合,即V={v|节点v是顶点},E={(v1,v2)|v1和v2是可见的}。如图1,CS图的顶点集合为 {1,q,2,3,4,5,6, 7,8},边集合为{(1,q),(q,2),(2,3), (3,4),(4,5),(5,1),(5,6),(5,7),(6, 7),(7,8),(6,8),(4,7),(4,8)}。

2.2 CS图的建立

2.2.1 确定CS图的顶点集

定义3:关键邻居。边界节点p的两个关键邻居为节点p在顺(和逆)时针方向沿着所在面的边界遇到的第一个凹点或凸点。用CN(p)表示边界节点p的关键邻居集合,如图1中,CN(p)= {1,q}。

为了构建CS图,首先需要确定顶点集合V。对于每个凸点p,CN(p)={p1,p2},若p1和p2不同时为凹点,则节点p是一个顶点。如图1,该方法确定的顶点集合为 {v1,v2,v3,v4,v5, v6,v7,v8},但此时忽略了顶点q,在2.2.2节建立CS图的边时将检测出顶点q。

以上方法要求每个凸点知道其关键邻居的信息。确定关键邻居的具体过程如下:每一个凹点和凸点发起包含自身信息的消息包,收到该消息的邻居节点q做以下处理:

1)若q为普通节点或者q的FID与发起者p的FID不同,那么q丢弃该消息包,不予处理;

2)若q的FID与p的FID相同,则继续转发;

3)若q为凸点或凹点,则停止转发该消息,q设置p为自己的关键邻居,并记下p的信息。

2.2.2 确定CS图的边集

CS图的边集合E定义为顶点集合中所有可见的两个顶点建立的最短路径集合。在确定CS图的顶点后,可见的两顶点建立最短路径即完成CS图边的建立。

判断两个顶点是否可见的方法如下:每个顶点建立到其他所有顶点的最短路径,如顶点v1和v2建立了一条最短路径,若该最短路径经过其他顶点,则说明v1和v2这两个顶点不可见;否则可见,且该路径则为CS图的一条边。CS图边上的点简称为边点,每个边点记录到其邻居顶点的跳数。如果存在凸点q在该最短路径上,则q为在2.2.3部分忽略的顶点。

每个节点需要存储CS图,只需存储CS图的顶点集合及顶点间的距离即可。CS图的大小与网络规模无关,只与网络中障碍物复杂度有关。

2.3 建立虚拟坐标

对于凸面上的节点,若其不是凸面边(即可见边)上的节点或顶点,则为凸面内部节点。我们观察到,当前网络中有以下4类节点:顶点、CS图边点、凸面内部节点以及网络中的其他普通节点。

每个节点p建立虚拟坐标向量,该向量包括两部分:VID坐标和距离坐标,分别记录p的可见顶点的ID号和到可见顶点的距离。建立坐标的方法如下:

1)若节点 p不是凸面内部节点,则p建立VID坐标{ID(v1),ID(v2),…,ID(vk)},vk是p的可见顶点,k是p的可见顶点个数;p建立距离坐标 (d1,d2,…,dk),dk是p到可见顶点vk的跳数距离;

2)若节点p是凸面内部节点,则p的坐标与距离p最近的边点坐标相同,并记录到边点的距离为偏移距离。如图 1,s的可见顶点集为 {v1, v5},假设s到v1的跳数为5,到v5的跳数为10,则s节点建立的 VID坐标为 (ID(v1),ID (v5)),距离坐标为(5,10)。

3 躲避障碍物的路由算法GRdo

为了以较短的路径躲避障碍物,GRdo首先依据源和目的节点的VID坐标判断两节点是否存在共同的可见顶点,若不存在,则借助CS图确定路径,否则,根据距离坐标确定路径。给定源节点s和目的节点t,s根据s和t的VID坐标判断出它们共同的可见顶点集合为CV={v1,v2,…,vk}, GRdo根据CV=Ø或CV≠Ø两种情况给出两个相应的子算法。

3.1 GRdo的两个子算法

3.1.1 GRdo_NCV算法

此算法针对源节点s和目的节点t无共同的可见顶点的情况,即CV=Ø。s根据可视图在多条路径中找出到t的最短路径,并记录该最短路径经过的可视图顶点数据包沿着该最短路径到达 t的可视顶点,然后递归调用VCBR策略确定到目的节点t的路径。如图1,s根据可视图确定最短路径为。

定理1:GRdo_NCV算法确定的路径为最短路径。

证明:首先证明该情况下的s和t互不可见。假设s和t不可视即线段st(用st表示)不与任何凸面相交,则一定存在距离st最近的顶点v,使得sv和tv都不与任何凸面相交,即v是s和t的共同可视顶点,这与s和t无共同可视顶点的条件相违背,所以s和t互不可视。由计算几何学可知,此时s到t的最短路径经过凸面上的某些顶点,该最短路径即为GRdo_NCV算法所确定的路径。

3.1.2 GRdo_CV算法

此算法针对s和t有共同的可见顶点的情况,并根据共同顶点所在面的信息分以下3种情况:

1)不存在两个共同可见顶点在一个面的情况,即CV≠Ø且任意两顶点vi、vj∈CV满足FID(vi)≠FID(vj)。s确定最短路径为s→vi→t,其中vi∈SV且使得路径最短。如图1,v6的VID坐标为(ID(v5),ID(v6),ID(v7),ID(v8)),s与v6只有一个共同可见顶点v5,确定路径为s→v5→v6。

2)存在两个共同顶点在同一面的情况,即CV≠Ø,vi、vj∈CV且FID(vi)=FID(vj),此时显然存在边 (vi,vj)∈CS图。源节点s采用如下算法判断s和t在直线vivj的同侧还是异侧:设与s距离最近的可见顶点为vk且FID(vk)= FID(vi),若vk≠vi∧vk≠vj,或者t符合上述情况,说明s和t在直线vivj异侧,否则s和t在直线vivj同侧。

定理2:上述判断算法总能正确地判断出s和t在直线vivj的同侧还是异侧。

证明:如图2,区域2和4内的所有节点的可见顶点集合中都包含vi和vj,在区域2内的节点,到该凸面的最近可见顶点一定为vi或vj,而区域4内的节点到该凸面的最近可见顶点一定不是vi和vj,如图中是vk(忽略了使区域4内节点对于vk不可见的小凸面),因此该算法可以判断出区域2和区域4内的节点在直线vivj的异侧且互不可见。

1)GRdo_CV异侧路由算法:若s和t在直线vivj异侧,此时可以应用GRdo_CV的情况1)算法确定最短关键路径为s→vi→t或s→vj→t。如图2,s与t有共同的可见顶点vi和vj,s在该面最近的可见顶点为vi,t在该面最近的可见顶点为vk,则s判断出其与t在直线vivj的异侧,并确定最短路径为

源节点s估算出d(s,t)后,采用贪心算法在邻居节点集合中选择d(s,t)最小的邻居作为下一跳节点,n表示s的邻居。若s采用贪心算法到达中间节点p,且p的邻居节点的可见顶点集合中不包含或时,说明p与t不是可见的,p递归调用GRdo算法确定到t的路径。如图4,s判断s、t有共同可见顶点且在直线的同侧,应用余弦定理估算出d(s,t),采用贪心转发算法,当到达节点p时,p无法应用贪心算法找到下一跳,且p存在邻居节点q,q对于不可见,则p递归调用GRdo算法判断属于GRdo_CV的情况1),采用GRdo_CV的情况1)算法确定路径为最终s到t的路径为

3)存在两个以上的共同可见顶点在同一面上的情况。即存在顶点集合CV,其中根据距离坐标,从CV中选择距离s最近的可见顶点和距离t最近的可见顶点vj,若则和作为被选择的两个共同可见顶点,此时s和t应用GRdo_CV同侧路由算法;否则任意选择vi的邻居顶点vk,应用GRdo_CV同侧路由算法。

3.2 GRdo算法描述及理论分析

基于以上两种子算法,GRdo的算法如下所示。

算法1 躲避障碍物的路由算法GRdo当前节点为u(包括源节点s),目的节点t 1:If(u、t的坐标相同)如果u、t的ID也相同,则GRdo算法成功找到目的节点t;否则说明 t是凸面内部节点,采用贪心算法根据偏移距离到达目的t。3:Else(判断由u、t的共同可见顶点情况) 4:If(u、t无共同可见顶点) 2:根据G Rdo_NCV路由算法,确定最短路径经过的可视图顶点为vi→vk→…→vl,→vj,此时应用贪心算法转发数据包到达vj,u=vj,goto行1。6:If(u、t在某面有一个共同可见顶点) 7: 根据G Rdo_CV情况1)路由算法,确定最近的可见顶点v,贪心地将数据包转发到顶点v,u=v,goto行1。8:If(u、t在某面有两个共同可见顶点vi和vj) 9:If(u、t在直线vivj异侧) 10:goto行7; 11:else 5: 12:应用G Rdo_CV同侧路由算法,贪心地选|sp(n,t)|最小的邻居节点 n,直到成功转发给 t,若遇到点p,且p的邻居节点的可见顶点集合中不包含vi或vj,u=p,goto行1。13: If(u、t在某面有两个以上共同可见顶点)根据GRdo_ CV情况3)下的选择算法选择出两个共同可见顶点vi和vj,g oto行9

综上所述,给定源节点及目的节点的坐标,源节点首先通过VID坐标判断共同可见顶点的情况,然后根据距离坐标或CS图采用相应的算法到达目的节点。若目的节点是凸面内部节点,到达坐标相同的边节点后,贪心地选择偏移距离递增的节点作为下一跳,最终达到目的节点。下面证明GRdo算法总能找到路径。

定理3:在网络空间连续的条件下,GRdo算法总是能够找出s到t的路径。

证明:根据GRdo算法的描述,GRdo首先判断源与目的节点间是否存在障碍物,若存在,则总是成功地将数据包转发到某个中间顶点,此时只需某顶点v总是能够找出到达t的路径。下面证明v与t至少有一个共同可视顶点v1,v1≠v,即可应用GRdo策略。因为v是t的可视点,即vt不与任何凸面相交,设v1是距离vt最近的顶点,则线段vv1和tv1都不与任何凸面相交,即v1是v与t的共同可视顶点,且由于网络中每个节点至少有两个可视顶点,所以必存在顶点v1,得证。

综上所述,GRdo在连续空间内总能保证找到路径。对于离散空间,由于GRdo_CV情况1)路由算法是以欧氏距离来度量路径长度,因而不能保证绝对避免死端节点,但网络节点密度较大时,节点间跳数距离近似于欧氏距离[8],保证了GRdo算法的有效性。由上述分析可知,GRdo_NCV, GRdo_CV情况2)和情况3)路由算法总能正确地判断出源与目的节点是否可见,并根据距离坐标或CS图确定最短路径,虽然GRdo_CV情况1)不能总是保证其确定的路径最短,但实验表明, GRdo总体确定的路径近似最短。

4 实验与结果分析

本节对GRdo和其它路由算法进行模拟对比实验以验证GRdo的实际性能。模拟环境设置如下: 7 989个传感器节点均匀随机地分布在一个存在障碍物的网格网络内,其面积为100 m×100 m。如图5所示,白色区域表示障碍物,黑点表示传感器节点。不失一般性,设每个节点随机分布在1 m× 1 m的网格内。通信半径设置为2 m;网络平均密度为8.66。本节将GRdo与以下两个基于虚拟坐标的路由算法进行比较:

1)VCAP路由算法:VCAP是一种基于3个信标节点的路由算法;

2)GLIDER算法:GLIDER考虑了网络中形状规则的障碍物问题,试验中共选择13个节点作为信标节点,其中8个位于网络边界,剩余5个位于障碍物边界。

本节共选取600组源与目的节点对进行实验,其中100组为随机选取的可见节点对;200组为随机选取的不可见节点对;剩余300组为随机的节点对。并通过贪心转发成功率和平均路径长度近似比两个参数来比较GRdo,VCAP和GLIDER的性能。

图5 网络拓扑图Fig.5 Network topology graph

定义4:贪心转发成功率(GFSR)。若一个数据包能够利用贪心转发算法到达目的节点,称该包贪心转发成功,即该类数据包不包含通过局部洪泛到达目的节点的数据包。贪心转发成功的数据包与总数据包数的比值称为贪心转发成功率。

定义5:平均路径长度近似比(APLS)。贪心转发成功的数据包所经过的路径长度与应用最短路径算法所确定的路径长度的比值称为平均路径长度近似比。

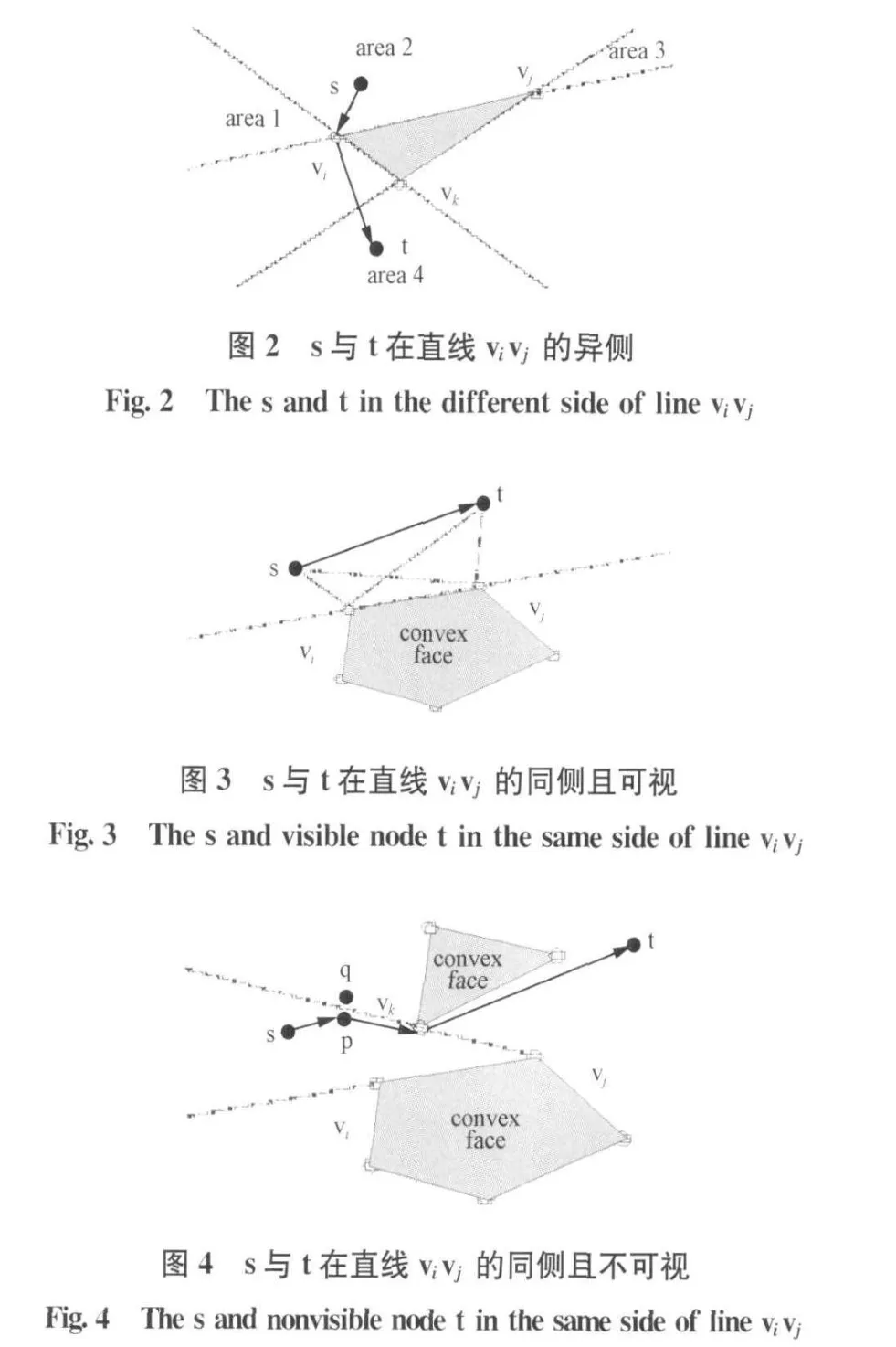
A.贪心转发成功率(GFSR)

GFSR的实验结果见图6。对于100组可见节点对,VCAP的GFSR为63%;对于200组不可见节点对,VCAP的GFSR为31%;而对于300组随机节点对,VCAP的GFSR仅为42%。这主要是由于VCAP算法仅利用3个节点作为信标节点,因此该机制确定的虚拟坐标不能够较好地反映出节点间的相对位置。所以,在存在障碍物的网络中,VCAP算法由于障碍物的干扰产生大量的“死端”节点,而这些 “死端”节点降低了该算法的GFSR。与VCAP相比,GLIDER算法的性能较好,该算法的平均GFSR可以达到75%。这是因为GLIDER算法随机选择多个障碍物附近的节点及障碍物的边界点作为信标节点,从而以这些信标节点为基准划分的子区域的复杂度与整个网络的复杂度相比有所降低,见图7。但是由于GLIDER算法随机地选取信标节点,不能保证较为规则的子区域划分。所以在GLIDER算法中,障碍物附近仍然容易产生 “死端”节点,这就降低了其GFSR。而本文针对障碍物的干扰提出的GRdo路由算法,对于3类节点对,其平均GFSR都可达到90%以上,相对于其它两种算法性能有较大提高。这表明GRdo在较大程度上解决了VCAP算法和GLIDER算法中 “死端”节点较多的问题,提高了转发成功率,减少了局部洪泛次数,从而节省了由洪泛产生的能量消耗。

B.平均路径长度近似比(APLS)

APLS的实验结果见图 8,其纵轴的参数APLS反映了该算法确定的路径长度。APLS越接近于1,表示该算法确定的路径越接近于最短路径。从图中可以看出,VCAP和GRdo算法的APLS值＜1.05,其路径长度与最短路径长度相差较小。而GLIDER的平均APLS为1.129,这是由于GLIDER为了避免数据包转发到障碍物附近的“死端”节点,采取 “绕道”的策略来躲避障碍物,该策略虽然有效地提高了GFSR,却增加了路径长度。

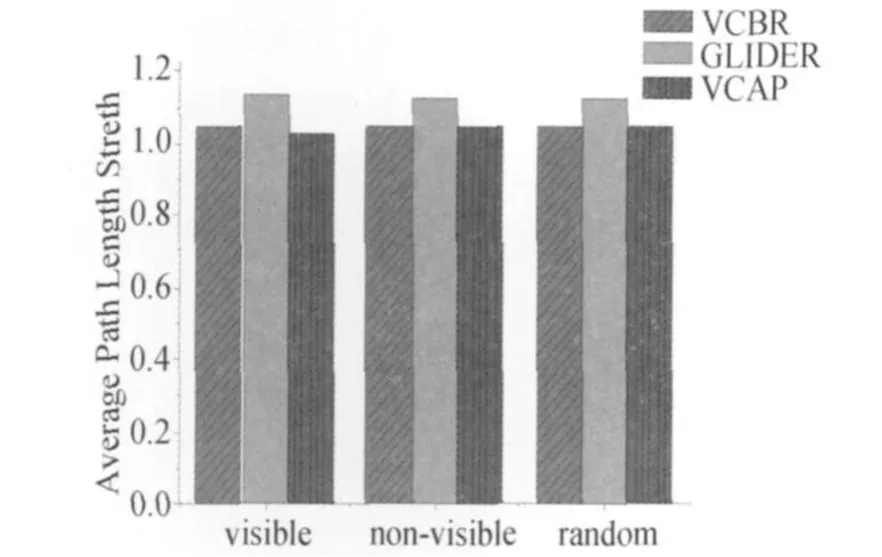
图8 平均路径长度近似比Fig.8 Simulation results of APLS

5 结论与未来工作

针对WSN中障碍物的存在问题,本文提出了一种分布式的路由算法GRdo。GRdo由节点的虚拟坐标估算出最短路径,针对不同情况根据距离坐标或CS图确定路径。理论分析和实验结果表明:在存在障碍物的网络中,本文提出的路由算法能够有效地降低丢包率,并得到较短的路由路径。未来工作包括设计一种考虑链路质量或时延等多方面因素的路由算法。

[1] Yujun Li,Yaling Yang,and Xianliang Lu.Routing Metric Designs for Greedy Face and Combined-Greedy-Face Routing[C]//INFOCOM'09,April,Rio de Janeiro,Brazil,2009:64-72.

[2]G.Tan,M..Bertier,and A.M.Kermarrec.Convex Partition of Sensor Networks and Its Use in Virtual Coordinate GeographicRouting[C]//.INFOCOM' 09,April,Rio de Janeiro,Brazil,2009:1 746-1 754.

[3]J.Bruck,J.Gao,and A.Jiang,MAP:Medial Axis based Geometric Routing in Sensor Networks[C]// MOBICOM'05,August,Cologne,Germany,2005: 88-102.

[4]H.Alt and E.Welzl.Visibility Graphs and Obstacleavoiding Shortest Paths[J].Zor-Zeitschrift fur Operation Research,1988,32:145-164.

[5]A.Caruso,A.Urpi,S.Chessa,and S.De.GPS Free Coordinate Assignment and Routing in Wireless Sensor Networks[C]//INFOCOM' 05,March,Miami, 2005:150-160.

[6]R.Fonseca,S.Ratnasamy,J.Zhao,et al.Beacon VectorRouting:Scalable Point-to-point Routingin Wireless Sensornets[C]//NSDI'05,May,Boston, 2005:329-342.

[7]Y.Liu,L.M.Ni,and M.Li.A Geography-free Routing Protocol for Wireless Sensor Networks[C]// HPSR'05,Hongkong,May,2005:351-355.

[8]Q.Fang,J.Gao,L.Guibas,et al.GLIDER:Gradient Landmark-based Distributed Routing for Sensornetworks[C]//INFOCOM'05,March,Miami,2005: 339-350.

[9]Y.Wang,J.Gao,J.S.B.Mitchell.Boundary Recognition in Sensor Networks byTopological Methods [C]//MobiCom'06,September,Los Angeles,CA, USA,2006:122-133.