基于数字脊波和样条权神经网络的高光谱图像融合分类

赵春晖,尤 佳

(哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001)

0 引 言

对于高光谱遥感图像进行数据融合和分类是当前研究的热点。文献 [1]提出了基于有限脊波变换(FRIT)的遥感图像融合算法,由于该变换存在 “折叠效应”,在脊波重构中不可避免地引入环绕噪声。针对有限脊波的这一缺点Donobo[2]等人构造了基于真实脊函数的脊波,并用快速 Slant Stack算法将其进行了数字化。人工神经网络 ( ANN)是实现高光谱图像分类的一种有效手段[2],但传统的神经网络(如:BP,RBF)存在着局部极小,收敛速度慢和初值敏感等缺陷,文献 [3]提出了一种全新的神经网络,并将其命名为样条权神经网络(SWNN),由于该网络的权值是输入样本的函数,因此它包含有训练样本的特征信息;由于该网络的计算量主要集中于线性方程组的求解,因此能很好地克服传统神经网络的缺点。本文将基于真实脊函数和快速Slant Stack算法的数字脊波和样条权神经网络引入高光谱遥感图像的融合分类中,结合局部信息熵(LIE)和主体投票(MV)规则实现了特征级和决策级的数据融合,结合AVIRIS图像进行了地物分类,并给出了仿真试验结果。

1 数字脊波变换

根据E.J.Candes提出的脊波变换模型,脊波变换是在Randon域进行的小波变换。实现脊波变换的数字化中最重要的一步就是Randon变换的数字化,其中较广泛应用的方法之一就是采用有限Randon变换 (FRAT),由于这种方法是在代数直线上的求和,因此存在 “折叠效应 (wraparound effect)”,在具体实现中会产生环绕噪声。文献[4]提出了一种基于快速slant stack算法的数字化方案,由于该方法是在几何直线上进行的求和运算,因此不存在 “折叠效应”的问题。Donoho等人将快速Slant Stack方法与脊波结合,建立了基于真实脊函数的数字脊波算法[5]。

1.1 快速Slant Stack算法

它实际上是沿直线y=sx+z对(u,su+z)的n个值进行求和,求和的值不是来自图像的原始空间,而是来自原始图像在v上的插值得到的图像˜I1(u,y),其第一个变量离散取值,第二个变量则是连续的。沿变量y方向的插值运算由式(3)给出,令m=2n,定义m阶Dirichlet核为:

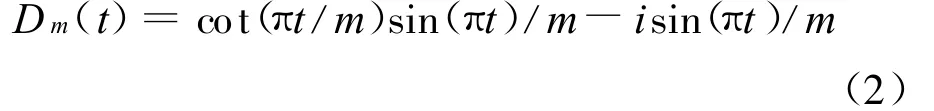
则有插值图像:

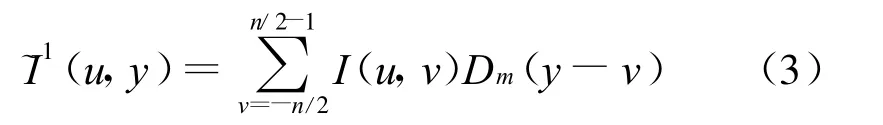
注意到这是一个内插核,因此有:

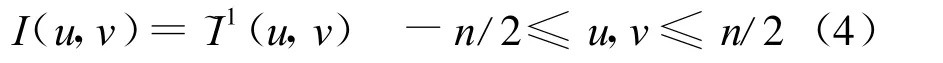
交换变量x和y,定义关于基本垂直直线组的Randon变换为:

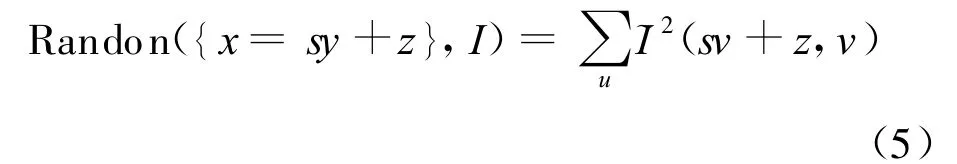
其中

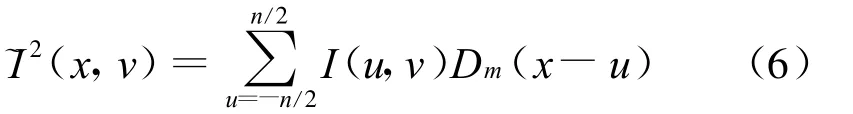
Slant Stack算子S:L2(dx)→L2(dtdθ)定义如下:

对于θ∈[-π/4,π/4]

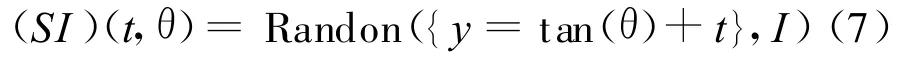
对于θ∈[π/4,3π/4]

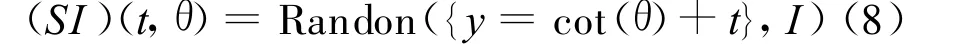
其中截距t满足-n≤t＜n。

它将n×n的矩阵I映射为2n×2n的矩阵SI。文献 [1]给出了相应的快速算法,并指出对于大小为n×n的图像,其计算量为O(NlogN),其中N=n2。

1.2 Meyer小波

设Ψj,k(t)≡Ψj,k(t;m)是m点离散周期Meyer小波,0≤k＜2j。对作离散Fourier变换得:

再作Fourier逆变换,得:

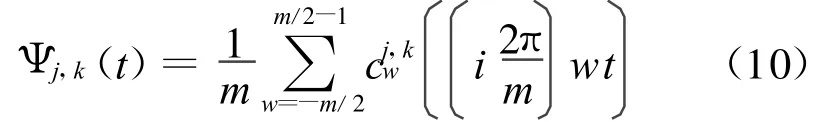
定义分数微分的Meyer小波如下:

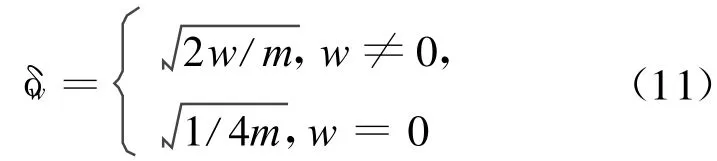
1.3 数字脊波

对于大小为n×n的图像I(u,v),中心为(0,0),且-n/2≤u,v＜n/2。定义满足:

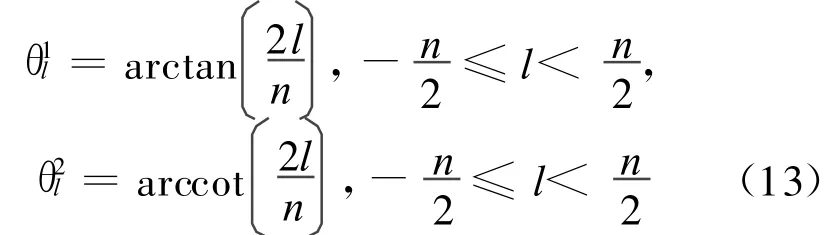
设n为给定的正整数,数字脊波ρj,k,s,l是一个从Meyer小波构造的n×n的脊函数矩阵,与Meyer小波的关系由式(14)给出:

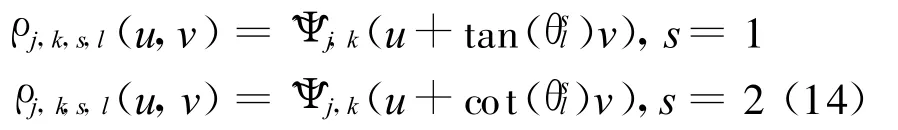
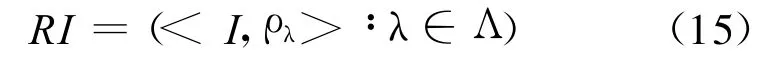
定理1指出了数字脊波变换 R和离散Slant Stack变换S以及Meyer小波变换W之间的关系:

定理1[5]数字脊波变换等价于作Randon变换后关于变量t作一维小波变换,即:

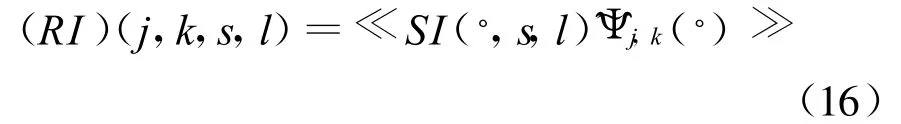
其中＜＜.＞＞表示仅对变量t进行的内积运算。且有下式成立:

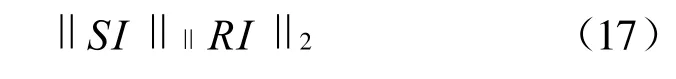
2 样条权函数神经网络

张代远提出了一种全新的人工神经网络[3],并将其命名为样条权函数神经网络。该神经网络与以往的经典神经网络(如:BP,RBF神经网络)存在着许多显著的优点:如训练后的神经网络是输入样本的三次样条函数,而不是常数,且能反映样本的信息特征;拓扑结构简单,只有两层(传统神经网络至少为3层),且只有输入层的权与神经元互连,输出层没有权;算法需要的神经元个数与样本数无关,仅取决于输入输出的节点个数;算法可将问题转化为显性方程组的求解,因而速度快,不存在传统算法的局部极小,收敛速度慢,初值敏感等问题。

2.1 神经网络的投影方程

一般而言,可认为神经网络完成的工作是实现多维(m维)输入到多维(n维)输出之间的映射。即:

由上式可知,只要给定输入 x,每个zi就确定了,即:

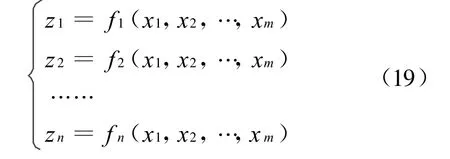
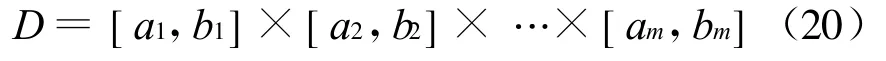
则一般来说,方程组(19)中的每一个方程都可以看成是给定区域的m+1维超曲线。对于给定参数t∈[ta,tb],xi(t)(i=1,2,…,m)在给定的区域有定义,则式 (19)中的每一个方程可以由以下参数方程表示:

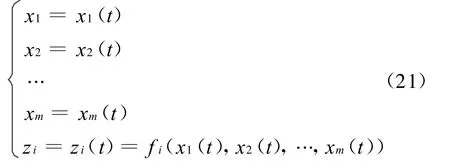
考虑将zi(t)(i=1,2,…,n)分别向xj(j=1,2,…,m)投影,可以得到xjOzi平面上的投影柱面方程:

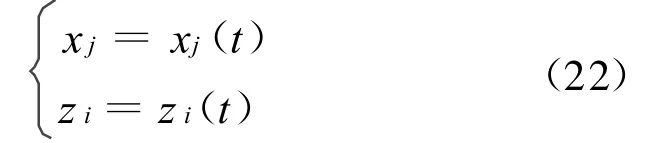
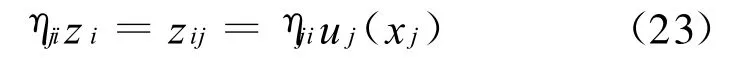
则参数方程(21)可以写成:

其中

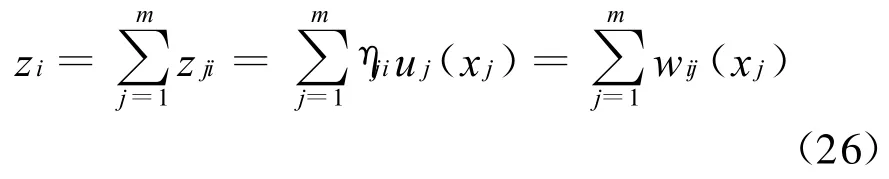
其中wij(xj)=ηjizi=ηjiuj(xj)=zji称为理论权函数,简称权函数。根据理论权函数的定义可以看出,它包含有投影曲线ui的信息,能在一定程度上反映原来空间曲线的特征,因此该权函数是具有真实物理意义的。由式(26)构造的基于理论权函数神经网络拓扑结构见图1。

2.2 样条权函数神经网络的拓扑结构与训练算法

神经网络训练的目的是为了求得权函数 wij (xj),一般来说,只有离散的有限样本点是已知的,这就意味着要通过有限个已知的样本点来求得理论权函数,而这一般来说是不可能做到的,但是可以通过插值的方法求得近似的权函数。

对于图1的结构,假设每个输入由m维向量构成,对于每个输出样本zi,共有N+2个需训练的样本,()表示对应第i个输出的神经元(由加法器Add构成)与第j个输入节点相连的理论权函数。由于有N+2个需要训练的样本,因此节点 xj将有N+2个输入量,可构成一个向量,记为:

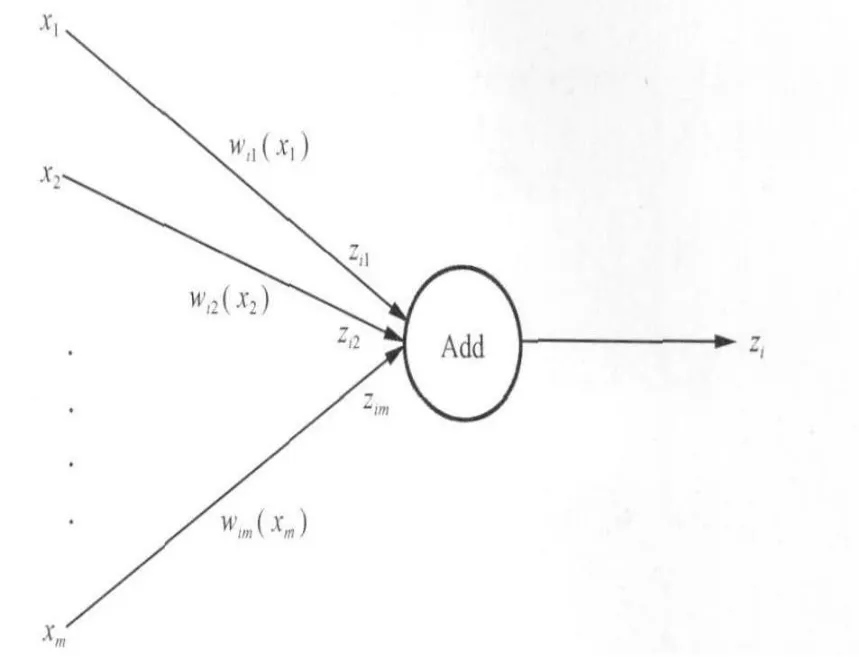
图1 基于理论权函数神经网络Fig.1 Neural network based on theoretical weight function

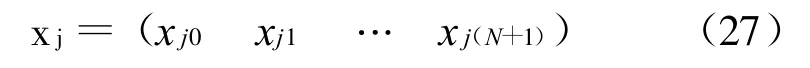
同样,将其对应的目标向量组成一个N+2维向量

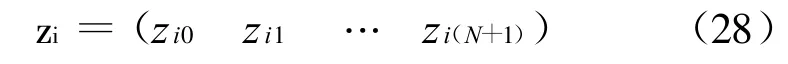
其中

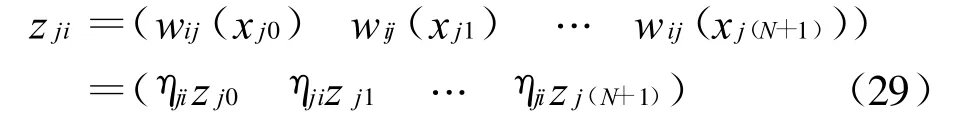
按照理论权函数对目标样本的分配方法,权函数wij(xj)的输入量由式 (27)给出,输出式由式(29)决定,所以对应的插值点为:

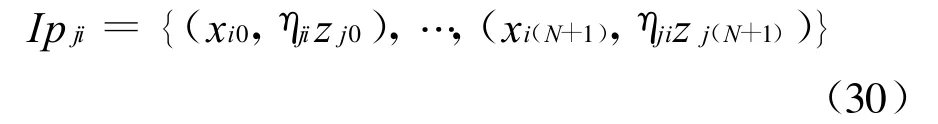
采用三次样条插值,样条函数为

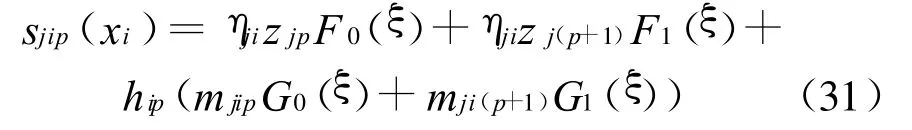
其中,F0、F1、G0、G1为 Hermit插值公式的参数,可以通过解线性方程组得到,结合具体的边界条件,可以求得三次样条函数的具体表达式,其详细过程参见文献 [2-3]。通过三次样条插值得到的上述神经网络被称为第一类样条权函数神经网络,其拓扑结构如图2所示。

3 高光谱遥感图像融合与分类

由以上讨论的基于快速Slant Stack算法的数字脊波变换和第一类样条权函数神经网络构造的高光谱图像融合系统可以实现特征层和决策层两个较高层次的数据融合。

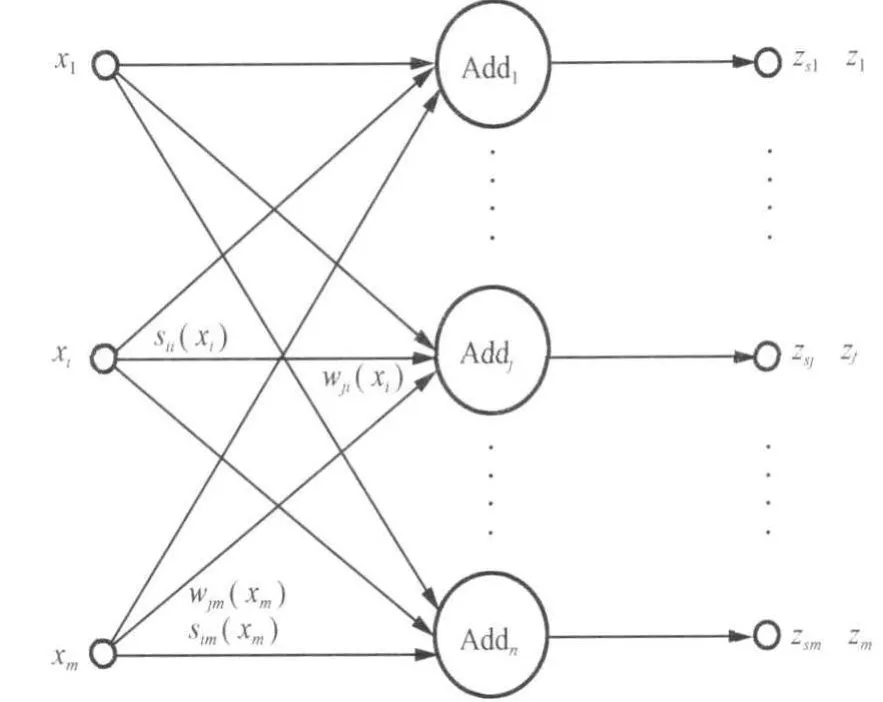
图2 第一类样条权函数神经网络Fig.2 First class spline weight function neural network

3.1 特征级融合及分类实现

特征级融合可以表述为FI-FO[6](Feature In -Feature Out),即实现由高维特征空间到低维特征空间的映射。基本思想是利用数字脊波变换在不同分辨率的数据中提取特征信息,然后送入样条权神经网络,神经网络输出分类结果。其中特征提取是该层次融合的关键。由式(16)可知数字脊波变换实质上是在Randon域进行的一维小波变换,因此本文提取的特征是基于一维小波变换后在不同分辨率水平上的局部信息熵。

窗口W(大小为M×Ni,Ni表示第i分辨率水平的步长)内的局部信息熵LIE(Local Information Entropy)为:

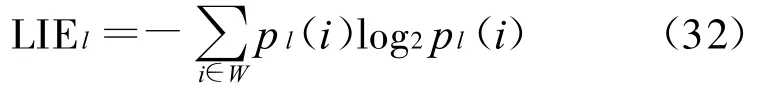
其中pl(i)表示第l波段图像局部窗口内出现像素值为i的概率。

考虑到基于快速Slant Stack算法的数字脊波变换将N×N的原始图像空间映射为2N×2N的像空间窗口选择M=2,Ni=2N/(2i)=21-iN, i表示小波分解的第i层 (i=1,2,3)。

局部信息熵可以用来衡量经小波变换得到的各低频分量和细节分量包含的局部信息的大小。因此基于局部信息熵的特征融合算法是对于各低频和细节分量根据其不同波段对应分量包含的信息量的大小给以不同的权值,信息量越大,权值越大。最终的融合权值还需要归一化,即在式(32)的基础上除以各波段同一位置局部信息熵之和。

以上可以实现高光谱图像的基于数字脊波的特征级融合,采用相应的重构算法即可实现图像的重建。

上述融合过程实际上是一个数据降维的过程,将降维后的数据送入样条权函数神经网络,结合由代表各类特征的标定样本训练得到的三次样条权就可以得到最终的分类结果。

3.2 决策级融合分类实现

决策级融合实现预分类器输出结果到最终分类结果的映射,即DEI-DEO(Decision In-Decision Out)。设为高光谱图像传感器的输出向量,将它分为N个波段组,则X=[]T,其中(i=1,…,N)可以表述为=[…,xi,di],di为第i个波段组包含的波段数。决策级融合分类原理框图见图3,先进行局部分类(Local Classification),然后将各局部分类器输出结果进行决策融合,输出最终分类结果。

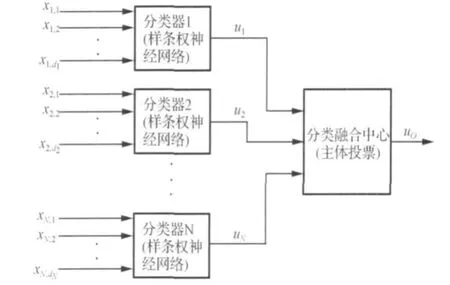
图3 决策融合系统框图Fig.3 Decision level fusion system flowchart

考虑到所处理的高光谱图像具有数据维数高的特点 (如AVIRIS图像包含220个波段的数据),为使实现局部分类的神经网络结构不至于太复杂和提高分类效率,在进行局部分类之前先将输入数据进行降维。降维方法有波段选择、自适应波段选择[7](ABS)、自适应子空间分解[8](ASD)、数据融合等。本文采用基于像素层的数据融合方法实现数据降维,融合策略是对于经过数字脊波变换的数据进行归一化方差加权[9]。

本地分类器选用第一类样条权函数神经网络,其拓扑结构见图2,其输入是经融合降维后的脊波系数,输出是局部分类判别结果。由于数字脊波系数包含有伪极傅里叶域[2](Pseudopolar Fourier Domain)的信息,因此此处权函数反映了原始图像在极坐标下的频域信息。对于分M类的情况本地分类器进行预分类输出结果ui=k(k=0,1,…,M-1),表示当前输入样本被判为属于第k类。

决策融合策略采用文献 [6]提出的基于主体投票法的思想:对于各本地分类器输出的分类结果进行主体投票,加权融合后得到最终的分类结果。主体投票规则 (Majority Voting Rule)可以表述为:

其中p(xi|wk)表示当前输入样本在第i个波段组被判为第k类的概率密度函数。若

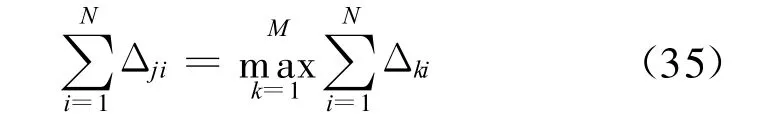
则该样本被判为属于第j类。

4 仿真及结果分析

采用典型的AVIRIS高光谱遥感图像作为实验图像,该图像取自1992年6月拍摄于美国印第安纳州西北部遥感实验区松树试验场,它包含了农作物和森林植被的混合区,它共有220个波段,每个波段图像大小为145行145列,其空间分辨率为20 m ×20 m,数据深度为16 bit。原始图像50(R)、27 (G)、17(B)波段假彩色图像见图4。

图4 假彩色图像Fig.4 Pseudo-color picture

去掉噪声和水汽吸收带,实验从220波段原始数据中选取200个波段作为研究对象,选取4类典型地物:大豆、玉米、草地、林地。所用训练样本和检验样本数见表1,其中训练样本总数为630,检验样本总数为1 406。

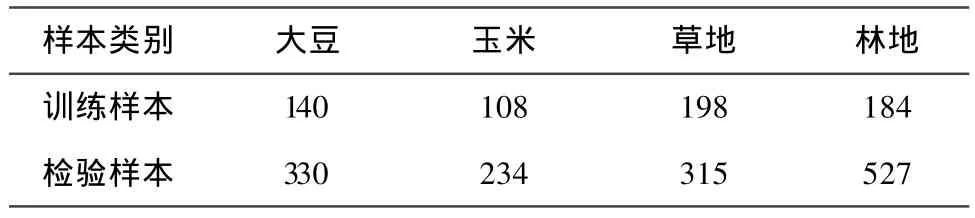
表1 类别及样本的选取Table 1 Type and sample selection

4.1 特征级融合分类结果分析

对于特征级融合,将200波段图像等间隔的分为5组,然后采用基于快速Slant Stack算法的数字脊波变换和局部信息熵进行融合。图5是基于以上融合策略和采用文献 [3]提出的基于局部对偶框架算法实现脊波重构得到的5个特征级融合图像之一。可以看出该图像存在一定程度上的模糊,分析原因,除了计算过程数据的截断误差(由双精度型数据直接转化为16bit无符号数据)这一主要原因外,另一方面也是由于特征降维带来的信息的丢失所引起的。

图5 数字脊波融合图像Fig.5 Digital ridgelet fusion picture

图6给出了基于特征级融合的不同方法得到的分类精度,所采用的训练与检验样本均相同。其中前4组是用作实验对照,它们都选择传统的极大似然(ML)分类器,特征融合处理手段依次为决策边界特征提取(DBFE)、文献[7]采用的基于小波变换(DWT)的特征融合、基于有限脊波变换(FRIT)的特征融合、基于本文所提到的用快速Slant Stack算法实现数字脊波变换 (DRT)和局部信息熵的特征融合。最后一组是采用2.1节提出的基于数字脊波变换和样条权神经网络(DRTSWNN)的特征级融合分类,其分类精度最高,可达到95.87%。以上分类精度的提高是以数据运算量的增大为代价的:对比第3组和第4组实验,它们的不同之处仅在于第3组采用的是有限Randon变换,它存在 “折叠效应”,第4组采用快速Slant Stack算法实现几何域的Randon变换,它避免了 “折叠效应”的出现,不会有环绕噪声的引入,但是处理数据量增大了4倍;对比第4组和第5组实验,它们的差别仅在于分类器的选择,第4组采用传统的极大似然(ML)分类器,第5组采用样条权神经网络(SWNN),前者结构简单分类的效率要高于后者。

另外,单从分类精度的数值结果上来看,文献[6]提出的基于投影追踪 (Projection Pursuit)算法的特征融合在较少的训练样本情况下分类精度可以达到96.2%,分析其原因,该方法充分考虑了样本的先验知识和真实地物空间信息,而本文提出的方法中均未加以考虑。

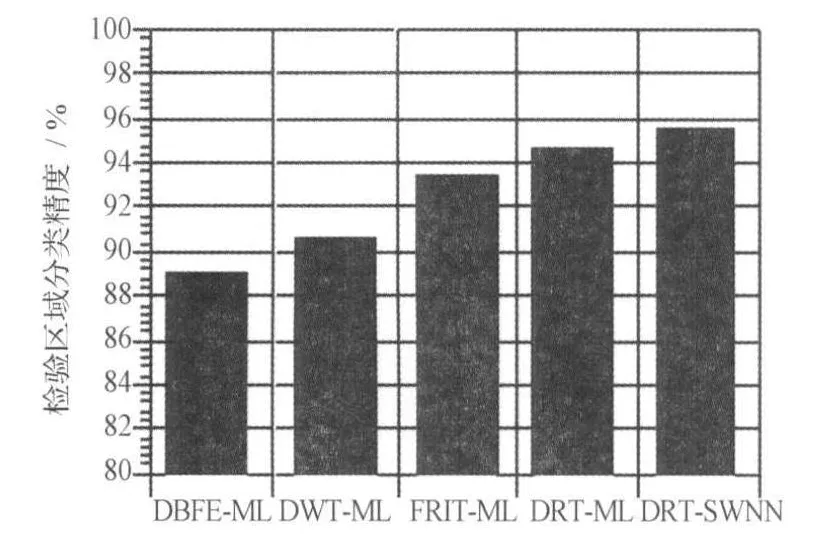
图6 特征融合分类精度Fig.6 Feature fusion classification accuracy

4.2 决策级融合分类结果分析

决策级融合先将各波段信息等间隔分成5组,每组将40个波段信息进行像素层融合得到4组融合后的脊波系数图像,然后将其送入局部分类器完成预分类。局部分类器选用第一类样条权函数神经网络。然后再用主体投票规则进行决策融合,得到最终的分类结果。局部分类器和决策中心分类器均采用与特征级融合分类相同的训练样本和检验样本。

分类精度见图7,其中第3组为本文采用的基于样条权神经网络(SWNN)和主体投票(MV)规则得到的,其分类精度为92.65%。其余3组用作实验对照:第1组为采用BP神经网络(BPNN)得到的结果,由于该方法效果与BP网络的初值的选取有很大关系,且容易陷入局部极小,图7中的结果是多次实验得到的最佳值;第2组是单独采用样条权神经网络(SWNN)得到的结果,由于该方案权函数求解可以转化为线性方程组求解来实现,因此不存在局部极小,初值敏感和收敛速度慢等传统神经网络存在的问题,因此该方法无论在分类精度的提高方面还是在计算复杂度上都明显优于第1组采用的BP神经网络的方法;第4组在预分类中选择极大似然 (ML)分类器实现局部分类,然后采用主体投票法实现分类决策融合。对比第3组和第4组实验,它们的不同之处仅在于局部分类器的选择上,本文方法略优于ML-MV方法,但其计算复杂度也要高于该方法。

对比图6和图7可以看出,以上决策级融合分类得到的分类精度较特征级融合分类有所下降,文献 [6]指出了其原因:这是由于在决策级融合策略中本地分类器和决策融合中心采用了相同的训练样本,这样容易使训练得到的结果不太具有一般性。避免该问题的方法可以选择不同的训练样本,但本文讨论的都是在非常有限的训练样本下实现融合分类的情况,这样做势必增加所需的训练样本数。

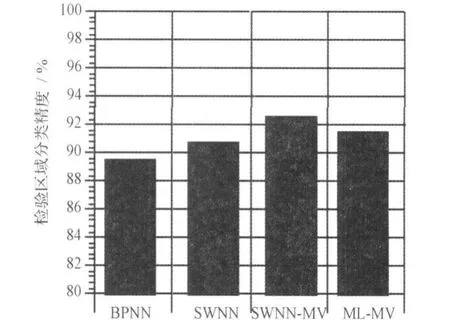
图7 决策级融合分类精度Fig.7 Decision level fusion classification accuracy

5 结 论

通过研究基于快速Slant Stack算法和真实脊函数的数字脊波变换和一种全新的样条权神经网络,本文提出了基于数字脊波变换和样条权神经网络的高光谱遥感图像融合分类的具体算法,实现了基于局部信息熵的特征级融合和基于样条权神经网络和主体投票理论的决策级融合,并在此基础上针对典型AVIRIS图像进行了地物分类,用较少的训练样本获得了良好的分类效果。实验表明采用数字脊波变换和样条权神经网络进行特征级和决策级融合是有效的。

以上方案均未考虑高光谱数据的先验知识和真实地物空间信息,这在一定程度上制约了分类精度的进一步提高。若能将各种先验知识也考虑进去进行多源数据融合必将获得更好的融合和分类性能。关于多源、多层次数据融合的研究是今后该开展的工作之一。

另外,采用快速Slant Stack算法实现的Randon变换数字化方案是以数据冗余的增加为代价的,若能找到既不会引入数据冗余又不存在 “折叠效应”的数字脊波实现方案,将能更好的为高光谱图像数据融合服务。数字脊波和样条权神经网络的这种松散式结合很容易让人联想到小波和神经网络的紧致性结合构成的小波神经网络,将脊波的良好时频局部特性和神经网络的良好自学习能力和容错性进行结合构造出脊波神经网络,也将能很好的为高光谱图像处理服务。寻求新的数字脊波实现方案和关于脊波和神经网络的紧致性结合也是下一步的研究内容。

[1]Tao Chen,Junping Zhang.Remote Sensing Image Fusion Based on Ridgelet Transform[C]//Geoscience and Remote Sensing Symposium,2005:150-1 153.

[2]张代远.神经网络新理论与方法[M].北京:清华大学出版社,2006.

[3]张代远.样条权函数神经网络的一种新算法 [J].系统工程与电子技术,2006,(9):1 434-1 437.

[4]A.Averbuch,R.R.Coifman,D.L.Donoho,et al. Fast Slant Stack:A notion of Randon T ransform for Data in a Cartesian Grid which is Rapidly Computable, Algebraically Exact,Geometrically Faithful and Invertible[EB/OL].http://stat.stanford.edu/～donoho/reports.

[5]Donoho D L,Flesia A G.Digital Ridgelet Transform based on T rue Ridge Functions[EB/OL].http:// stat.stanford.edu/～donoho/reports.

[6] Luis O.Jimenez,Anibal M orales,Antonio Creus. Calssification of Hyperdimensional Data Based on Feature and Decision Fusion Approaches Using Projection Pursuit,Majority Voting,and Neural Networks[J]. IEEE Trans on Geoscience and Remote Sensing.1999, 37(3):1 360-1 366.

[7]Chunhong Liu,Chunhui Zhao,Wanghai Cheng.Hyperspectral Image Classification by Second Generation Wavelet Based on Adaptive Band Selection[C]// IEEE ICM A Proceedings.NiagaraFalls,Canada. 2005.

[8]Zhang Ye.Adaptive Subspace Decomposition for HyperspectralData Dimensionality Reduction[C]// ICIP99 Proceedings.1999:326-329.

[9]刘春红,赵春晖.基于提升算法的超谱遥感图像融合分类研究 [J].哈尔滨工程大学学报,2004,25(6): 794-798.