拦截导弹自适应动态滑模制导

陈兴林,花文华

(哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001)

0 引 言

滑模控制方法对于外部干扰和系统参数的摄动具有较强的鲁棒性,且并不局限于系统类型的约束,已在目标拦截情形中获得了广泛研究。周荻[1]基于线性化的拦截导弹和目标相对运动关系给出了一种自适应滑模制导律;佘文学[2]考虑一阶目标机动动态特性,对其进行了扩展;周军[3]研究了基于二阶滑模控制的驾束制导导弹一体化制导系统设计方法;Brierley[4]将滑模控制应用于拦截导弹与目标非线性相对运动情形以实现空空拦截;Moon[5]基于滑模控制方法给出了一种目标机动有界的比例导引类制导律。

在滑模控制中,如果控制结构的切换具有理想的开关特性,则能在切换面上形成理想的滑动模态,渐进趋近于原点。但是在实际的工程中,由于时间上的延迟和空间上的滞后等原因,滑动模态呈抖振形式,光滑的滑动上叠加了抖振,因此抖振是影响滑模控制广泛应用的主要障碍。而上述文献都采用了准滑模控制[6],即将符号函数采用饱和函数或连续化的继电特性代替,虽然一定程度上削弱了抖振,但系统性能也被折中。为降低抖振,本文将不连续的项,即符号函数项转移到控制的一阶导数中去,得到一种在时间上本质连续的动态滑模控制律。同时与自适应控制思想相结合,给出了一种自适应动态滑模制导律。

1 自适应滑模控制

在对文献 [1]和文献 [2]深入研究的基础上,针对多变量非线性系统给出自适应滑模控制的一般方法。系统状态方程为:

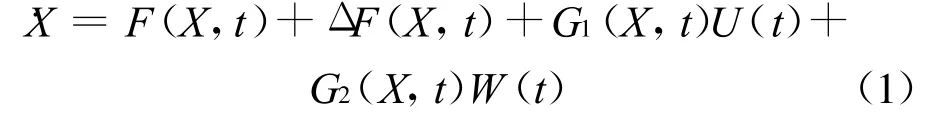
其中X∈Rn,U∈Rm,W∈Rl分别为系统的状态变量,控制输入和外界干扰;F(X,t),G1(X, t),G2(X,t)为已知的相应维数的状态变量X和时间的函数;Δ F(X,t)为系统的结构摄动。

假设非线性系统式(1)满足如下假设条件:

1)0＜‖W(t)‖≤a,a＞0定常;

2)Δ F(X,t)=E(X,t)δ(X,t),E (X,t)∈Rn×n已知,‖δ(X,t)‖≤b,b＞0定常。

在滑模控制系统设计中,为了消除系统中结构摄动以及外部扰动的影响,一般需要预先设定不确定性的范数界,然而在工程实际中,这个范数界往往很难精确给出。为了更好地解决这一类系统中实际可能存在的不确定性控制问题,采用自适应的思想实现对于系统结构摄动和外部干扰的不变性。

定义滑模切换面:

其中,C∈R1×n为定常的。

基于Lyapunov稳定性理论进行滑模控制律设计。定义Lyapunov函数为:

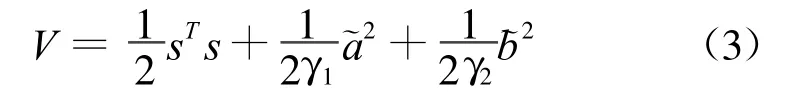
对式(3)两边求导:

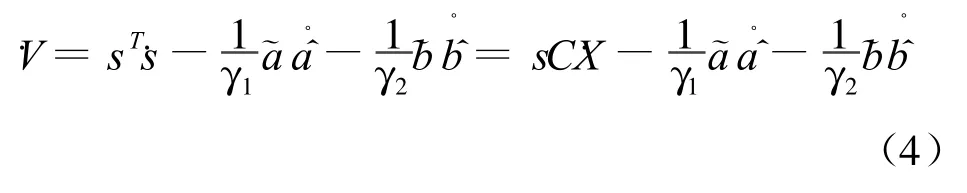
结合式(1),

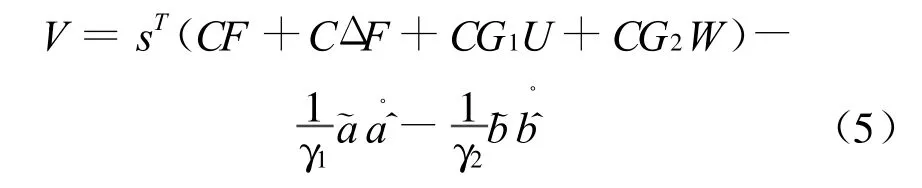
假设CG1非奇异,取控制向量U为:

其中,K,ε＞0为指数趋近律系数。

将(6)式代入式(5),并结合干扰和不确性有界假设,由式(5)可得到:

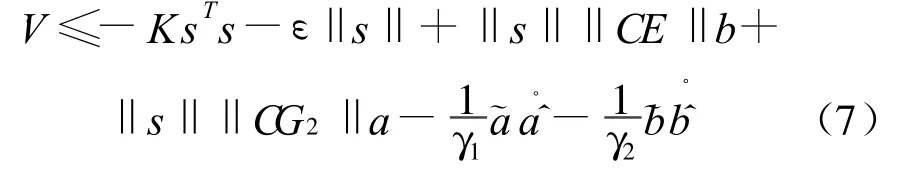
取

则由式(7)可以得:

取自适应律为:

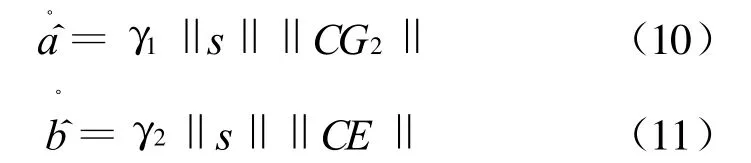
故

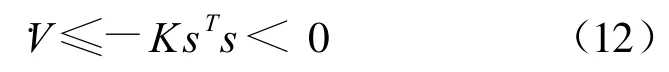
由式(12)可以得到:

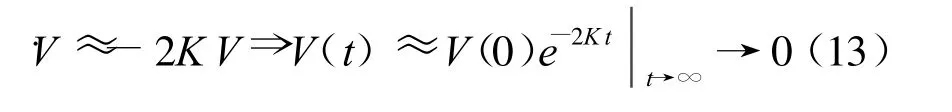
综合以上分析,对于如系统(1)所示的多变量非线性系统,有下述定理成立:

定理(自适应滑模控制律):由式(1)所描述的多变量非线性系统在干扰和不确性有界及CG1非奇异条件下,采用控制律式(14)和自适应律式(10)和式(11),可实现滑模切换面式(2)的渐近收敛。

2 动态滑模制导律

拦截导弹和目标相对运动关系,如图1所示。图中θ为视线角;r为拦截导弹和目标的相对距离;θm和θt分别为拦截导弹弹道角和目标航向角。建立相对运动方程:

其中,vr,vθ分别为沿视线方向上和视线法向方向上的相对运动速度。

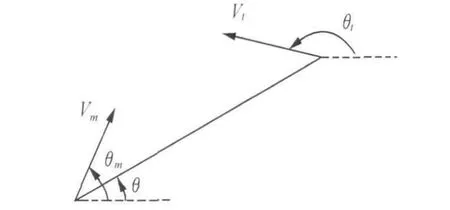
图1 平面导弹和目标运动关系Fig.1 Planar geometry of missile and target

假设拦截导弹和目标速率为常值,对式 (15)和式(16)两边求导,并进一步转化可以得到:

其中˙θ表示视线转率;uθ和ωθ分别为视线法向上的拦截导弹控制量和目标机动干扰。

式(18)可进一步表示为:

两边求导:

Δ F=[0 0]T无系统结构摄动,G2为二维单位阵。

定义滑模切换面和Lyapunov函数:

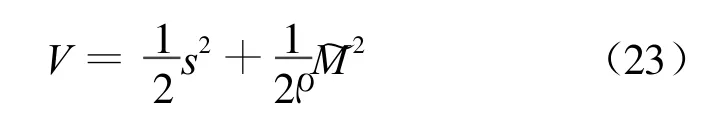
则结合自适应滑模控制律定理可以得到拦截导弹渐进收敛滑模制导律为:

自适应律为:

由式 (24)可以发现,第一项c|vr|˙θ为传统的比例制导律,而最后一项为不连续控制项,将不连续项,即符号函数项转移到控制uθ的一阶导数˙uθ中,以得到在时间上本质连续的动态滑模控制uθ,从而降低抖振的影响。K＞0为滑模趋近速率调节参数,取K=μ|˙r|/r,μ＞0,使得趋近速率同样具有自适应性,其物理含义为由于|˙r|在整个拦截过程中变化较小,滑模趋近速度随着导弹和目标之间的距离进行调整,特别是当导弹和目标相对距离r→0,趋近速度显著增大,可以避免视线转率的发散,减小抖振,确保对目标的稳定跟踪,从而减小脱靶量。

3 仿真验证

假设目标在拦截平面内视线法向上做正弦机动ωθ=10gsin(π t),初始拦截导弹和目标相对距离r0=5 000 m,vr0=500 m/s,vθ 0=30 m/s,c=4, ρ=0.1,μ=4。仿真结果见图2～图5。

图2 视线法向上相对速度变化曲线Fig.2 Relative velocity normal to line of sight

从图中可以看出,采用所给出的自适应性的动态滑模制导律,视线法向上相对运动速度及其导数经过1.5 s左右的调整时间以后,最终稳定在零值附近,实现了对滑模切换面的收敛,且抖振现象不明显;所需的指令加速度与目标的机动加速度可以较好的保持一致,说明该滑模制导律等速趋近项对目标机动具有较好的自适应能力;视线转率变化幅值不大,基本是稳定的,表明系统可以获得良好的制导精度,可实现对连续高机动目标的有效拦截。

4 结 论

1)滑模制导律对于系统中存在的结构参数摄动和外界干扰具有不变性,将目标机动视为一类具有有界扰动的不确定因素,因此所提出的滑模制导律具有很强的鲁棒性。

2)基于Lyapunov稳定性原理所确定的自适应律,实质上是对外界不确定因素的估计,引入这种适应律可以改善系统的稳定性和控制特性,从而提高导弹的制导精度。

3)采用动态滑模进行制导律的设计,将不连续控制项转移到控制的一阶导数中去,得到在时间上本质连续的动态滑模控制,有效降低了抖振的影响。

4)所设计的滑模制导律对于连续高机动目标具有很好的跟踪性能,而且不需要太多的观测信息,控制结构相对简单,易于工程实现。

[1]Zhou D,Mu C D,Xu W L.Adaptive Sliding-mode Guidance of a Homing Missile[J].Journal of Guidance,Control and Dynamics,1999,22(4):589-594.

[2]佘文学,周 军,周凤岐.一种考虑自动驾驶仪动态特性的自适应滑模制导律 [J].宇航学报,2003,24 (3):245-249.

[3]Zhou J,Wang T.Integrated Guidance Control System for Beam-riding Guidance Missiles Based on Second Order Sliding Mode Control[J].Journal of Astronautics, 2007,28(6):1 632-1 637.

[4]Brierley S D,Longchamp R.Application of Slidingmode Control to Air-air Interception Problem[J]. IEEE Transactions on Aerospace and Electronic Systems,1990,26(2):306-325.

[5]Moon J,Kim Y.Design of Missile Guidance Law Via Variable Structure Control[J].Journal of Guidance, Control,and Dynamics,2001,24(4):659-664.

[6]刘金琨.滑模变结构控制MATLAB仿真 [M].北京:清华大学出版社,2005:44-45.