角加速度边界层观测器设计
2010-03-14邓红星王宪彬
邓红星,王宪彬,刘 咔
(1.东北林业大学交通学院,哈尔滨150040,1969dhx@163.com;2.哈尔滨工业大学航天学院,哈尔滨150080)
伺服控制系统大多以位置和速率跟踪为目标,经典的PID控制在控制工程中受到了广泛的应用.但是,对于机器人、数控机床、机械手等许多高精度伺服系统,存在着负载、模型参数的大范围变化以及显著的非线性因素,使得传统的伺服控制方法难以满足高速高精度定位和跟踪以及低速平稳运行等要求.目前,尽管基于现代控制理论提出了多种先进控制方法,如自适应控制、非线性补偿控制、智能控制等,但均因实现十分复杂而很少被实际应用.因此,如何既能实现相对简单的控制方法,又能解决高速高精度和低速平稳性问题,已成为伺服控制系统研究的重点.研究表明,引入加速度反馈是解决这一问题的有效途径.
基于加速度反馈的控制方案多用在机器人控制方面,它不仅很好地解决了系统对于外界扰动的抑制问题,而且能很好地克服摩擦非线性、谐振等,从而对系统的跟踪精度也有很大提高,是一种强鲁棒控制方法.但是,由于加速度信号的获取一直是个难点,因而,加速度反馈没能得到广泛的应用.由于加速度反馈所需的加速度计存在价格过高以及加速度计本身的限制性条件,使得直接对加速度进行测量的代价很大,在很多场合下甚至难以使用.因而,根据光电码盘或其他位置测量元件的信号处理技术来获得加速度信号不失为一种很好的策略.G.Sulligoi和R.C.Kavanagh[1]提出了一种基于DSP和FPGA的CSDA测量方法,利用高精度时钟来检测低速时相邻角位置输出脉冲之间的时间间隔,试验表明具有一定的实用性; Toshiaki Tsuji[2]等人在M/T测速法的原理基础上,提出了一种S法来测量加速度,根据角位置变化来实时同步地更新加速度值,其精度比直接差分然后低通滤波要好很多;J.D.Han[3]等人利用卡尔曼滤波与牛顿预测相结合来估计角加速度,并应用到实际的机器人控制中,在10 Hz带宽内取得了很好的控制效果;Mariko Mizuochi[4]等人将倍频采样法运用到基于干扰观测器的加速度控制系统中,并用DSP和FPGA实现了这一方法,试验表明具有很好的控制效果;其他不同的方法诸如FIR[5]滤波以及基于观测器理论的Luenberger观测器[6-8]、自适应观测器[9-11]也分别得到了广泛的研究.但是,这些算法多考虑线性系统的加速度观测问题,动态响应性能不够理想[12].
本文以光电编码器角位置传感器输出的离散信号作为角加速度观测器的输入信号,考虑机电系统内部Stribeck摩擦、负载变化及外部扰动等非线性确定因素的影响,基于滑模控制的思想,提出一种边界层观测器设计方法,提高角加速度的观测性能,并给出相应的观测器动态性能分析和实验结果.
1 边界层观测器结构

图1 永磁同步电机系统方框图
角加速度观测器原理是通过综合测得的反馈信号和被控对象模型的知识,利用一定的控制原理来重构系统的状态,能更精确地认知被控对象的特性,并给系统控制律提供反馈信号.常规的Luenberger观测器针对线性系统具有很好的观测性能,但对于非线性伺服系统,Luenberger观测器对于外扰的观测收敛速度过于缓慢,缺乏对参数摄动的自适应能力,因而有必要研究非线性观测器.
1.1 对象模型
本文以交流永磁同步电机系统作为研究对象,其结构框图如图1所示.其中,u为计算机发出的模拟电压指令,Ku为电机驱动器的等效增益,KT为电机的力矩系数,Ke为电机的反电势系数,Kp分别为电流回路控制器的增益系数,J为电机及负载的总惯量,L为等效电感,r为电机绕组的等效电阻.摩擦力矩、负载变化以及电机的波动力矩均可看成包含在扰动力矩Tl内.
系统输入u到角位置输出θ的开环传递函数表示为

式中:R=r+Kp为系统等效电阻,K0=KuKp/Ke为系统开环等效增益,Tm=RJ/KTKe和Te=L/R分别为机械时间常数和电气时间常数.
1.2 观测器结构
基于1.1小节中的伺服系统数学模型,与实际系统相比,没有考虑实际系统中存在参数不确定因素,如不同负载条件下转动惯量J的变化,不同运行条件下电机驱动器等效增益的变化Ku等,也没有考虑实际系统中存在的摩擦或饱和非线性特性以及系统运行过程中电压波动、风扰等外部扰动因素的影响.
假设被控对象的所有参数不确定性、非线性和外扰均可用总扰动Tl表示,忽略电机系统的电气时间常数,则被控对象模型可用二阶系统来表示,因而,可得到用微分方程描述的被控对象的标称模型:
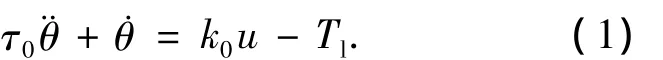
式中:θ为测量的角位置,u为控制输入,τ0和k0分别为实际对象的标称机械时间常数和等效增益.
本文将滑模控制与边界层观测器理论将结合,研究角加速度观测器的设计问题.
结合式(1),若以实际角位置θ和控制输入u作为观测器的输入,以观测的角加速度作为输出,则边界层观测器可用如下方程描述:
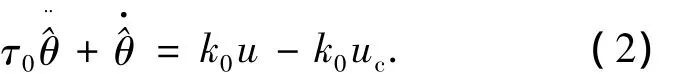
式中:^θ为观测器的角位置输出,uc为观测器的控制输入.如果^θ能完全跟踪系统的真实角位置θ,比较式(1)和(2),则有

由此可见,若uc能理想地观测系统中所有参数不确定性、非线性和外部扰动,则^θ可以很好地跟踪系统的真实角位置θ,从而得到理想的角加速度输出值,此时,uc的设计尤为重要.
本节将基于滑模控制思想来设计uc.由于滑模控制具有迅速响应,对参数变化及扰动不灵敏等特点,因而根据标称模型建立起来的边界层观测器,即使实际系统存在较大不确定性或外部扰动,观测器也能根据角位置误差的变化及时地调整控制量uc,使得^θ快速地跟踪系统的真实角位置θ,从而获得期望的角加速度估计值.
边界层观测器的结构如图2中虚线框所示,其中,u和θ分别为实际系统的控制输入和测量角位置,G(s)表示实际系统,G0(s)为实际系统的模型表示,e=θ-^θ为角位置观测误差,^a为角加速度的观测值.滑模控制用于在线估计扰动力矩Tl,其输入为角位置观测误差e,输出为控制量uc.

图2 边界层观测器结构
2 观测器的设计
基于滑模控制的观测器的设计关键在于如何确定观测器的输入控制量,本节重点阐述控制量uc的确定方法和观测器的动态分析.
2.1 控制量的确定
边界层观测器的设计主要在于设计控制量uc,为了得到控制输入uc,令
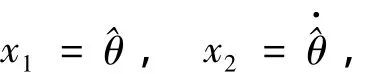
将边界层观测器(2)表示为状态空间形式,有

令

则式(3)可写成更一般的形式

定义如下的滑模面函数:

式中:θ为测量的角位置,λ为一正常数.当观测器的状态向量到达滑模面σ=0后将在滑模面内滑动,此时系统的动态品质由滑模面的参数λ决定,而与系统参数、扰动的影响无关,从而实现不变性.
若令

则滑模面函数可写成

观测器设计的目的是使观测器的状态满足σ=0.为了使观测器的状态能从任意初始位置到达滑模面,采用常数趋近律

定义Lyapunov函数

则对于任意非零σ,均有

上式表明,在任意初始位置均能保证σ→0.根据上述趋近律,可得误差微分方程

可以看出,观测器的暂态由极点-λ,-D决定.由滑模面函数(4)和趋近律(5)可得

令
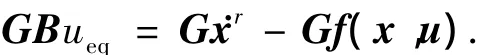
考虑到实际系统采用计算机实现边界层观测器,将上式应用Euler近似可得

式中:T为采样时间,k为正整数.进一步变换,有
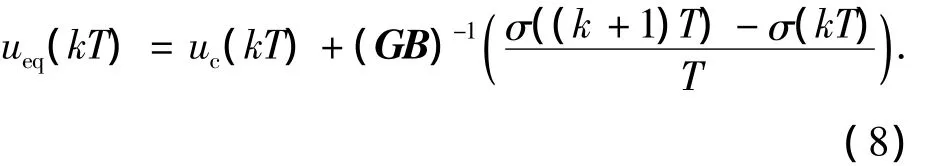
式(8)表明,为得到第k步的控制量,需要k+1时刻的σ((k+1)T)值,这对于实际物理系统显然是无法实现的.
考虑到ueq是一个连续函数,则认为ueq的当前值近似等于前一时刻的值,即

再由式(7)的Euler近似表达式可得到控制量uc的离散化表示

其中:离散滑模面函数σk表示为

令ek=θk-^θk,从而得到观测器的控制输入为


2.2 角加速度观测器的性能分析
2.2.1 动态性能分析
由式(6)可见,边界层观测器的暂态性能由极点-λ,-D决定,D选取过大,实际系统将因惯性等原因在滑模面高频穿越,而D选取过小,观测器趋近于系统真实状态的调节时间过长,不能实现快速跟踪.
2.2.2 稳定态精度分析
由于在计算离散控制律时,采用了Euler近似法,因而式(2)近似的结果必然会带来跟踪误差,即σ必将偏离期望的滑模面σ=0,首先分析因采用Euler近似计算对角加速度估计误差的影响.将式(7)进行积分可得到

应用Euler积分,式(10)可表示为

式中:O(T2)为Euler积分引入的积分误差,与式(9)联立可得

由式(11)可见,稳态误差取决于采样时间T的选择.
2.2.3 收敛区间分析
由于 ˙xr与f均为有界平滑函数,若令

则有
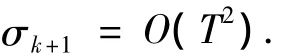
同样可以证明,在采样时刻

仍然有


当|σk|>O(T2),则有

式(12)表明,σk总是收敛到滑模面σ=0领域内的一个边界层内,这个边界层厚度的数量级为O(T2),而式(13)表明,σk一旦到达这个边界层,它将总是保持在这个边界层内.
3 实验结果
考虑图1所示的机电系统,其摩擦力矩约为10 N·m,摩擦力采用Stribeck模型,在系统开环情况下,角加速度观测器输出的角加速度与系统的真实加速度做如下两组对比实验,实验分析中,取λ=500,D=500,T=0.1 ms.
3.1 带有摩擦非线性的角加速度信号观测结果
图1所示的机电系统以频率1 Hz,幅值350 (°)/s2做角加速度正弦运动时,角加速度信号受摩擦等扰动力矩的影响,在峰值附近发生突变,角加速度信号观测结果如图3所示.图3中,实线为真实角加速度,虚线为观测角加速度,图4为图3的局部放大.

图3 含有摩擦时的角加速度观测响应

图4 角速度过零时的角加速度观测
可以看出,边界层观测器对加速度的观测能力很好,在摩擦力占主导成分的零速阶段,观测器有一定的超调和振荡,但是很快趋于稳定,相比于传统的角加速度观测方法,边界层观测器的观测结果动态特性好,跟踪精度高.
3.2 带有负载变化的角加速度信号观测
图1所示的机电系统做频率为15 Hz的正弦运动,边界层观测器在10 kg负载条件下的角加速度信号观测结果如图5所示,当负载增大到10倍(100 kg)时,角加速度信号观测结果如图6所示.由结果可以看出,即使对于负载变化很大的系统,边界层观测器仍然具有良好的跟踪性能和观测精度.这正是由于边界层观测器利用了滑模控制的不变性,实现了边界层观测器良好的观测性能.

图5 标称负载下角加速度信号观测结果

图6 角载变化时角加速度信号观测结果
4 结论
1)针对角加速度反馈所需的角加速度信号,提出了基于滑模控制的角加速度边界层观测器设计方法.
2)基于滑模控制方法设计的边界层观测器具有很好的动态观测性能和鲁棒性,观测误差处于期望滑模面的一个很小的边界层内.
3)本文提出的观测器算法简单,适合应用计算机实现,具有很好的实用性,为实现角加速度反馈控制提供了有力的基础.
[1]SULLIGOI G,KAVANAGH R C.An Innovative method for improved real-time measurements of angular acceleration in motion control systems[J].International Symposium Power Electronics,2006,21:1-5.
[2]TOSHIAKI T,HIROSHI K.Robust Acceleration Control Based on Acceleration Measurement Using Optical Encoder[C]//IEEE International Symposium on Industrial Electronics.Caixanova-Vigo,Spain:Institute of Electrical and Electronics Engineers Inc,2007:3108-3113.
[3]HAN J D,HE Y Q,XU W L.Angular acceleration estimation and feedback control:An experimental investigation[J].Mechatronics,2007,17(9):1-9.
[4]MARIKO M,TOSHIAKI T.Multirate sampling methed for acceleration control system[J].IEEE Transactions on Industrial Electronics,2007,54(3):1462-1471.
[5]VALIVIITA S,VAINIO O.Delayless Differentiation Algorithm and Its Efficient Implementation for Motion Control Applications[J].IEEE Transaction on Instrumentation and Measurement,1999,48(5):967-971.
[6]LORENZ R D,VAN PATTEN K W.High-resolution velocity estimation for all-digital ac servo drives[J].IEEE Trans Industry Application,1991,27(4):701-705.
[7]BODSON M,CHIASSON J,NOVOTNAK R T.Nonlinear speed observer for high-performance induction motor control[J].IEEE Trans Industrial Electron,1995,42(4):337-343.
[8]DAMIANO A,GATTO G,MARONGIU I,et al.Rotor speed estimation in electrical drives via digital second order sliding differentiator[C]//European Control Conference.Kalrsruhe,Germany:[s.n.],1999:15-21.
[9]KOUHEI I,SEIICHIRO K,KIYOSHI O.Wideband Motion Control by Acceleration Disturbance Observer[C]//International Power Electronics and Motion Control Conference.Portoroz,Slovenia:Institute of Electrical and Electronics Engineers Inc,2006:361-366.
[10]DE JAGER B.Acceleration assisted tracking control[J]. IEEE Control Systems Magazine,1994,14(5):20-27.
[11]GODLER I,INOUE M,TAMOTSU,et al.Robust comparison of control schemes with disturbances observer and with acceleration control loop[C]//IEEE International Symposium on Industrial Electronics.Bled,Slovenia:IEEE Piscataway,1999:1035-1040.
[12]HAN J D,WANG Y C,TAN D L,et al.Acceleration feedback for Direct-Drive motor system[C]//Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems.Takamatsu,Japan:Institute of Electrical and Electronics Engineers Inc,2000: 1068-1074.
