基于窗口无关均值滤波的MSR图像增强

王科俊，熊新炎，任 桢，付 斌

(哈尔滨工程大学自动化学院，哈尔滨150001，wangkejun@hrbeu.edu.cn)

Retinex方法由Edwin Land［1］提出，用来表示人类视觉中对光照和色彩的感知模型，将图像视为亮度图像和反射图像的组合.Land［2-3］进一步将随机步进计算(全局Retinex)进行了扩展，提出了中心/环绕对立操作(局部Retinex)［4］.Hurlbert等［5-6］研究了Retinex和其它光照理论的特性，发现了共同的数学函数，认为中心/环绕的这种空间对立形式对于在任意的光照条件下估计相应的反射光是一种通用的解决方法.对于局部Retinex，很多文献给出不同的方法，如单尺度Retinex(Single Scale Retinex，SSR)［7-8］，多尺度 Retinex (Multi-scale Retinex，MSR)［9-10］.这些方法都采用高斯核函数提取图像低频信息.这就需要在处理过程中进行大量的卷积运算，尤其是在多尺度Retinex方法中，需要进行3次大尺度的高斯滤波，当处理的图像为彩色图像时，要对RGB颜色频段分别进行3次大尺度高斯滤波，这将大大降低算法的运算效率，尤其是对实时性要求比较高的场合，是完全无法满足要求的.文献［10］中采用递归快速近似高斯方法(RMSR)，代替高斯卷积，使算法的速度得到了很大的提高，但仍不能满足实时的效果.Wang等［11］根据大尺度高斯卷积模板的加权值相近的特性，提出用量化均值滤波的方法替代高斯卷积，从而大大减少了运算时间.但其所采用的均值滤波方法效率不高，也无法满足实时处理的要求.本文在采用量化均值模板替代高斯卷积模板的基础上，提出一种与滤波窗口无关的快速量化均值滤波方法，从而大大提高了处理速度，并能实现良好的图像增强效果.通过与几种快速Retinex方法进行比较，采用RMSR的方法相比，则运算速度提高了近20倍，比文献［11］中的方法速度提高了近10倍.试验结果证明了该方法的有效性.

1 多尺度Retinex(MSR)方法

Land的Retinex理论认为图像由光度图和反射图两部分构成，如S=R·L.其中，R为反射图，L为光度图，S为实际获得的图像.Jobson等在文献［7］中用环境函数对原图像的卷积来近似光度图，并给出了单尺度Retinex变换的表达式

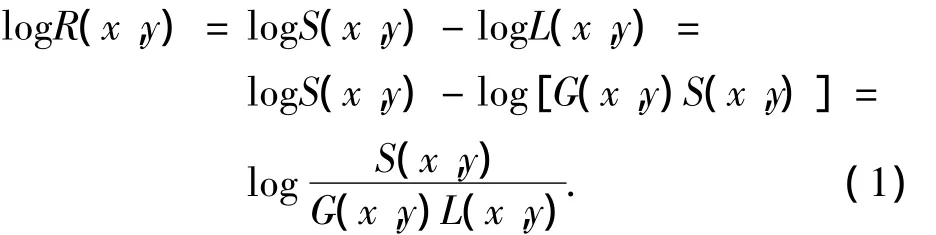
式中:G为环境函数，通常选用高斯函数［12］.

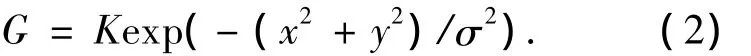
Hurlbert等对SSR进行了扩展，采用不同尺度的环境函数Gn对原图像进行卷积来近似光度图，通过Retinex变换得到一组不同尺度下的Retinex输出，将这些Retinex输出进行加权求和，提出了MSR方法.

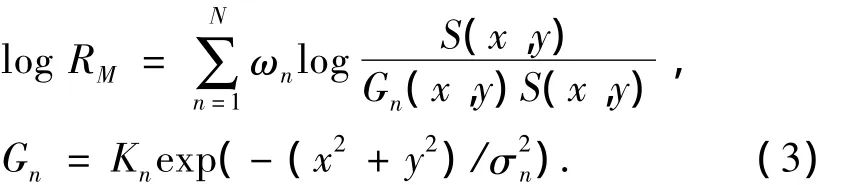
式中:ωn为加权系数，通常n取3，ωn取1/3，结合式(3)可以看出，执行1次MSR变换，需要进行3次高斯卷积，通过大量试验可知，标准差σ的范围通常选择σ1＜50，50＜σ2＜100，σ3＞100，这种选择的依据主要是由于光谱由不同频段的光线组成的缘故［13］.在本文的实验应用中，对于不同尺寸的图像，MSR的高斯标准差σ的取值根据大量实验分析都选定为30，90和200.可以看出，如果采用高斯卷积的方法进行计算，运算量是巨大的.

2 高斯卷积模板的均值特性

高斯卷积后的图像信息为图像的低频信息，高斯模板卷积可认为是加权平均过程.当选用较大的高斯尺度时，其卷积模板数值近似相等.如图1中的高斯卷积模板所示，为σ=200，模板大小为129×129的高斯加权矩阵.由于高斯模板中的数值非常接近，而且高斯模板权值的和近似等于1，所以可以用该129×129的模板均值近似代替模板中的权值.如图1中可取高斯模板的近似均值为0.609 4×10-4.

图1 大尺度高斯卷积模板

可以看出0.609 4×10-4≈1/(128)2，由此对1/(128)2的求取可以用移操作来代替，即右移14位.进一步可以看出，当高斯尺度选择适当时，可以用量化的均值模板代替高斯卷积运算.由文献［11］可知，当σ=30时，卷积模板大小取值33× 33，近似均值为9.4×10-4.当σ=90时，卷积模板大小取值65×65，近似均值为2.367×10-4≈1/(64)2，可以用右移12位替代.通过上述分析，可以看到，大尺度高斯卷积可以由3次大尺度量化均值滤波替代.图2给出了几个大尺度的高斯滤波图与对应尺度的均值滤波图的比较.可以看到大尺度的高斯滤波图与对应尺度的均值图十分接近.采用均方差当量表达式(M·N)进行分析，其中，M，N分别为图像的宽和高，gi，j，mi，j分别为高斯滤波图像和均值滤波图像上对应的(i，j)点的像素值.当σ=30均值模板为33×33时，求得均方差为V=1.298，当σ=90均值模板为65×65时V=2.526.当高斯核的标准差选定为30，90和200时，分别采用高斯滤波和均值滤波的方法对多幅图像进行滤波分析，并利用给出的均方差公式求解两种滤波方法的滤波图方差V，进一步确定，对应σ=30，90，200的高斯模板，均值模板大小分别在(30-40)，(60-70)，(125-135)之间时，方差V能获得最小值.

图2 大尺度高斯滤波图与对应尺度的均值滤波图

3 窗口无关快速均值滤波

3.1 FMF(Fast mean filter)方法

FMF方法是由Rakshit等［14］提出的快速均值滤波方法，该方法利用相邻滤波窗口之间的递归关系，对两相邻滤波窗口中重叠部分的像素和进行保存，仅对变化部分进行计算，实现计算的简化，提高运算速度，如图3所示.

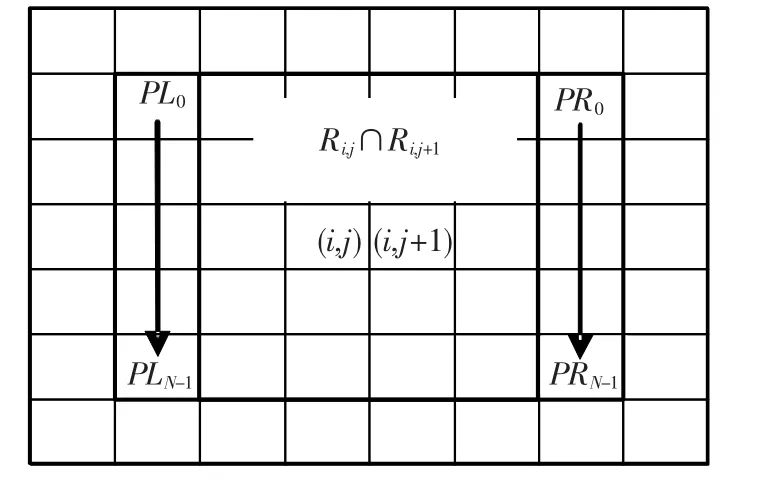
图3 相邻滤波窗口之间的递归关系

由图3可以看出，当滤波窗口中心由(i，j)点横向移到(i，j+1)点时，两窗口的相交区域为图3中部黑色框区.那么在求(i，j+1)的均值时，交集中像素点灰度值之和便不用重新计算，其滤波均值可以通过(i，j)点为中心的窗口区域的滤波值减去其最左边一列像素点PLn(n=0，…，N-1)灰度值之和后(图中左侧黑色框区)，然后用再加上(i，j+1)点滤波窗口中最右边一列像素点PRn(n=0，…，N-1)灰度值之和(如图3中右侧黑色框区)就可以得到.同理当窗口沿纵向移动时，也可通过上述递归方式进行计算.由于每次都要计算滤波核窗口的左右两侧像素列的和，所以该方法的运算量与窗口的高度是相关的，而不是与滤波窗口无关的.窗口递归公式为

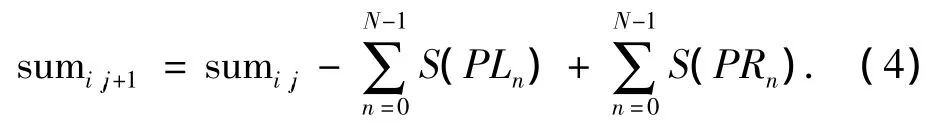
3.2 窗口无关均值滤波算法

FMF方法在对每个点进行均值滤波时，都要对当前滤波窗口的最左列和下一滤波窗口的最右列像素值进行累加，如滤波窗口大小为N，则对每一点将产生额外的2N次加运算.如果能先建立一个数组，其中已经分别存储了这两列像素灰度值的和，那么这2N次加法操作就能够避免.

从这个角度出发，建立一个维数为图像宽度M的一维数组s，每个数组元素中的值如图4所示，为滤波窗口横向所经区域的每一列的像素和，例如s［1］的值就是图4中黑色框所圈列的像素和.数组s在滤波窗口每一次换行后，还要进行更新，如图5所示，当滤波窗口由第i行换到i+1行后，原s数组的元素si［j］的值要加上对应列的(i+1+ry，j)点的元素值，同时减去(i-ry，j)点的元素值，生成更新后的si+1［j］值.其中，i为行，j为列，ry为滤波窗口纵向的半径.由此窗口递归公式为

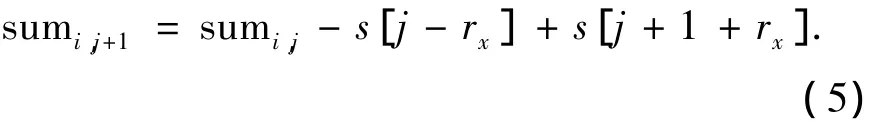
式中:rx为滤波窗口的横向半径.由式(4)和式(5)可以看出，式(5)在每一个像素点处减少了2N次加法操作时间.

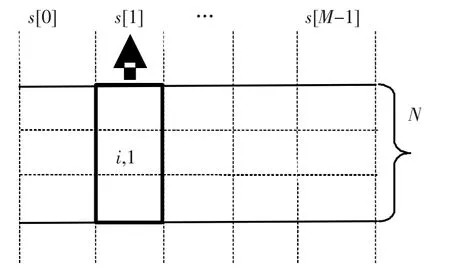
图4 横向滤波对应的s数组

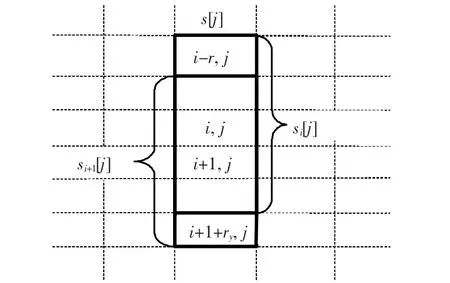
图5 滤波窗口换行时s数组的更新

本文的窗口无关滤波算法的关键就是建立数组s，数组s的建立分2个阶段:1)初始化;2)数组更新.其初始化过程为:

循环1:j:0～W-1

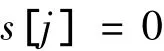
循环2:i:-ry～ry

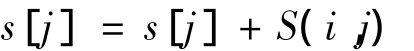
终止2

终止1

其中:ry为滤波窗口y轴方向半径，S(i，j)为(i，j)点的像素值.

对数组s的更新，更新公式为

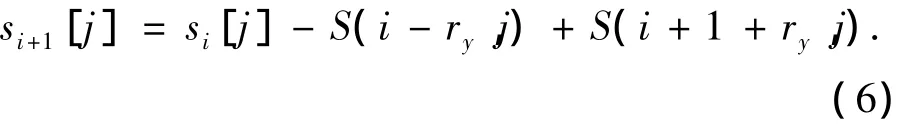
式中:S(i-ry，j)为在(i-ry，j)点的像素值.

由此窗口无关快速均值算法的实现过程为:循环1:i:0～H-1

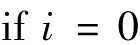
初始化数组s else

循环2:j:1～W-1

计算sum=sum-s［j-1-rx］+s［j+rx］和D(i，j)=sum/NK

终止2终止1

其中:H为图像的高，K为滤波窗口的宽.

结合提出的量化均值滤波，将滤波过程中的1/NK由高斯模板的近似均值量代替.

4 实验比较分析

采用窗口无关均值滤波的MSR方法对图像的增强效果与SSR和MSR方法的比较如图6所示，可以看出，本文的方法在图像增强的效果上与MSR方法基本一致，而SSR方法在对阴影中的猫的处理中可以看到，由于只采用单尺度高斯滤波，产生了光晕失真.由此可见量化的均值滤波对大尺度高斯卷积的近似替代是合理的.实验中，原始MSR的高斯标准差σ的3个值选定为30，90和200;SSR的高斯标准差选定为90;用于替换MSR的高斯滤波模板的均值滤波模板的尺寸，分别为33×33，65×65和129×129.

图6 几种Retinex方法的增强处理效果比较图

表1中给出了用均值卷积核代替原高斯核时，对图像增强效果的损失的定量分析.分析的图像为图6中给出的山坡、猫和街道图.用均方差当量表达式计算两种情形下增强后图像的均方差大小.对于彩色图像，则分别对RGB 3个通道进行了比较.可以看出采用均值卷积核代替高斯核对图像的MSR结果产生的损失很小，对图像的亮度和RGB彩色通道的像素数值改变都很小，不影响增强的效果.

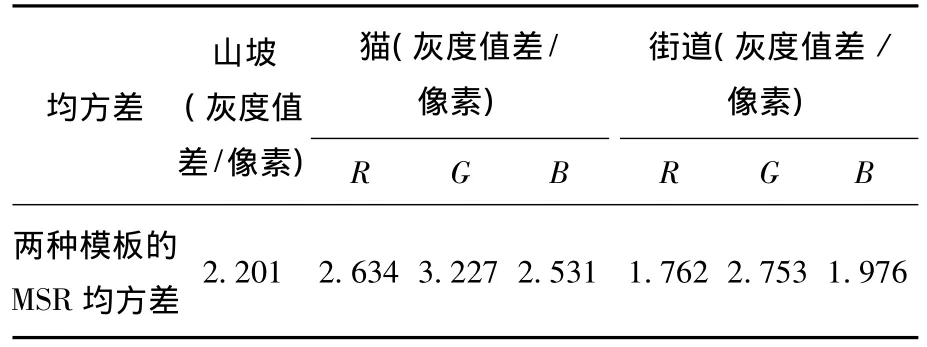
表1 均值卷积核代替原高斯核的图像均方差分析

均值卷积核的MSR方法和高斯卷积核的MSR方法在对图像的增强效果上十分接近，它们对于自然场景下单光源和多光源的图像都具有非常好的增强效果，对红外图像也具有很显著的增强效果［15］.本文方法在保持增强效果的同时，针对算法的速度进行了很大的改进.表2给出了本文方法与MSR方法和快速递归高斯滤波的MSR方法(RMSR)以及文献［11］中的方法在对不同尺寸的图像，在RGB空间上进行处理时，所用的时间的比较.表2中所列算法均在CPU为Pentium III 1200 MHz，内存为512 M的电脑上运行.

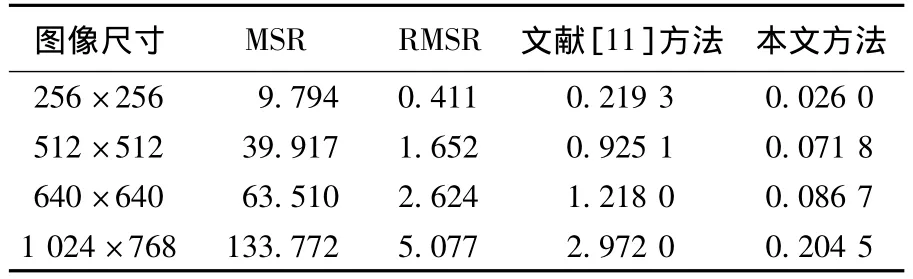
表2 多种Retinex方法在处理时间上的比较 (t·s-1)

由表2可以看出，文献［10］中采用的RMSR方法也是与卷积模板大小无关的，其计算效率相比MSR虽然有了极大的改进，但是仍无法令人满意.相比RMSR文献［11］的方法在计算效率上又有了进一步的提高，但是其滤波算法却是和滤波窗口的高相关的，因此其运算效率在图像尺寸进一步增大时，将无法满足实时处理的效果.而本文提出的窗口无关量化均值方法不但满足了图像增强的需要，在处理速度上也更加迅速，完全可以满足实时处理的需要.

5 结论

1)从大尺度高斯卷积模板可由量化的均值模板近似替代这一角度进行分析，提出了一种窗口无关的量化均值Retinex方法，并将该方法与其它几种快速Retinex方法在处理时间上和处理效果上进行了比较;

2)提出了一种与滤波窗口无关的快速均值滤波方法，并在多尺度Retinex方法中利用提出的快速均值滤波近似替代大尺度高斯卷积;

3)通过与其他多种快速多尺度Retinex方法在处理时间和处理效果上进行比较，证实了本文提出的快速多尺度Retinex方法在处理时间上的快速性和处理效果上的显著性.

［1］LAND E H.An alternative technique for the computation of the designator in the retinex theory of color vision［J］.Proceedings of the National Academy of Science，1986，83(10):3078-3080.

［2］LAND E H.Recent advances in retinex theory and some implications for cortical computations［J］.Proceedings of the National Academy of Science，1983，80(16): 5163-5169.

［3］LAND E H.Recent advances in retinex theory［J］.Vision Research，1986，26(1):7-21.

［4］HURLBERT A C.The Computation of Color［D］.Massachusetts:Massachusetts Institute of Technology，1989.

［5］HURLBERT A C.Formal connections between lightness algorithms［J］.Journal of the Optical Society of America，1986，A(3):1684-1693.

［6］HURLBERT A C，POGGIO T A.Synthesizing a color algorithm from examples［J］.Science，1988，239 (4839):482-485.

［7］JOBSON D J，RAHMAN Z U，WOOSELL G A.Properties and performance of a center/surround Retinex［J］.IEEE Trans on Image Processimg，1997，6(3):451-462.

［8］刘家朋，赵宇明，胡福乔.基于单尺度Retinex算法的非线性图像增强算法［J］.上海交通大学学报，2007，41(5):685-688.

［9］RAHMAN Z U，JOBSON D J，WOODELL G A.Retinex processing for automatic image enhancement［J］.Journal of Electronic Imaging，2004，13(1):100-110.

［10］王彦臣，李树杰，黄廉卿.基于多尺度Retinex的数字图像X光图像增强方法研究［J］.光学精密工程，2006，14(1):70-76.

［11］WANG Wen，LI Bo，ZHANG Jin，et al.A fast multiscale Retinex algorithm for color image enhancement［C］//Proceedings of the 2008 International Conference on Wavelet Analysis and Pattern Recognition.Hong Kong:IEEE，2008:30-31.

［12］KIMMEL R，ELAD M，SHAKED D，et al.A variational framework for Retinex［J］.International Journal of Computer Vision，2003，52(1):7-23.

［13］笍义斌，李鹏，孙锦涛.一种图形去薄雾方法［J］.计算机应用，2006，26(1):154-156.

［14］RAKSHIT S，GHOSH A，SHANKAR B U.Fast mean Filtering Technique［J］.Pattern Recognition，2007，40(3):890-897.

［15］雷美容，杨进华，张金泉.基于Retinex理论的红外图像的边缘增强算法［J］.长春理工大学学报，2008，31(2):11-13.