潜艇近水面舵减横摇的改进变结构控制

金鸿章，潘立鑫，王琳琳

(1.哈尔滨工程大学自动化学院，哈尔滨150001，panlixin1@sina.com;2.内蒙古工业大学信息学院，内蒙古呼和浩特010051)

航向调节和航迹保持是潜艇水平面操纵控制的两种主要形式.潜艇在近水面航行时，水平面操纵控制的重点一般放在航向调节上［1］.当对潜艇操纵方向舵作水平面的回转运动时，由于潜艇水平面运动方程具有强烈的非线性和耦合影响，会伴随出现另外两个坐标平面上的耦合运动，即横摇、纵摇和潜浮运动.造成横摇的原因在于回转中各横向力的作用点与艇的重心不在同一高度，横向力对重心形成了横摇力矩.此外，潜艇在近水面航行时所受的波浪干扰力矩也是产生横摇的主要原因.以往的水平面航向调节系统对转向过程中的横摇运动不采取主动控制，只是设置一个最大横摇限制器，通过主动降速的方法来减小过大的横摇幅值，因而横摇过程的控制品质一般［2］.为解决这一问题，Ming Chung Fang等［3-5］进行了深入的理论研究.他们从分析潜艇非线性运动模型入手，采取了对航向、横摇的主动控制，成果较为显著.

本文依据潜艇舵减横摇的原理［6-7］，在近水面非线性运动模型基础上，利用变结构控制方法分别设计了航向控制器和横摇控制器，这样既可以保证航向调节，又实现了对横摇运动的主动控制.由于变结构控制理论本身所带来的抖动影响及一阶波浪力的作用，使潜艇横摇、航向保持是围绕平衡位置上下变化，同时，舵角的输出也发生了抖动.为了削弱抖动，减小系统存在的稳态误差(艏摇和横摇)，必须要对原变结构控制方法进行改进.神经元具有自学习，自适应能力强的优势，利用自适应神经元的学习能力对变结构控制的趋近率进行在线修正，解决变结构控制系统中的抖振问题，这对于进一步改善潜艇水平面操纵性能具有重要意义.

1 近水面潜艇航向、横摇控制器设计

1.1 潜艇近水面运动模型

1967年由美国泰勒海军研究和发展中心(DTNSRDC)提出的潜艇标准运动方程已被广泛承认和应用，具有很高的权威性，但标准运动方程非常复杂，并且存在严重的非线性和参数的不确定性.因此，为了对实际运动研究的方便，提出了简化的运动仿真方程.考虑到控制系统设计的简单性和航向机动时运动的非线性，通过计算机仿真实验进一步筛选，得到如下用于进行变结构控制器设计的潜艇水平面运动数学模型:

1)横向方程.

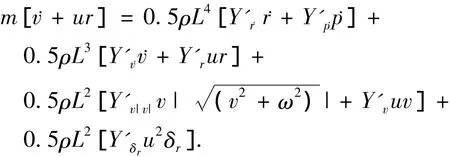
2)横摇方程.

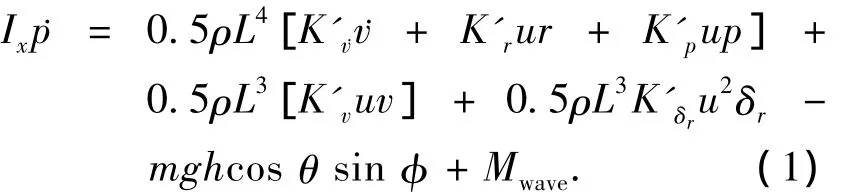
3)偏航方程.

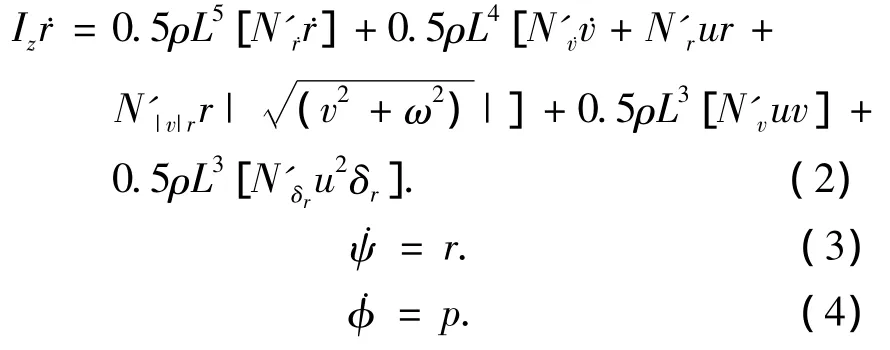
其中:m为潜艇质量(kg);L为艇长(m);h为潜艇稳心高(m);u为潜艇航速(m/s);v为横荡速度(m/s);ω为垂向速度(m/s);p为横摇角速度(rad/s);φ为横摇角(rad);q为纵摇角速度(rad/s);θ为纵摇角(rad);r为艏摇角速度(rad/s);ψ为航向角(rad);δr为 方向舵舵角(rad);g为重力加速度(m/s2);ρ为海水密度(kg/m3);Ix，Iy，Iz分别为绕x轴，y轴，z轴的转动惯量;X'(·)，Y'(·)，Z'(·)为无因次水动力系数; K'(·)，M'(·)，N'(·)为无因次水动力矩系数.

横摇方程(1)中，Mwave是潜艇所受到的横摇波浪力矩，当潜艇在近水面航行时，横摇波浪力矩作为干扰项，是必须加入的.实际采用的操舵角δrreal的取值如下:

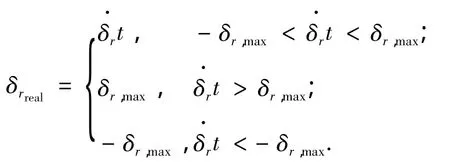
1.2 波浪干扰的描述

在研究舰船运动时，常采用的波谱是单参数的Pierson-Moskowitz波谱［8］，Pierson-Moskowitz波谱密度公式为

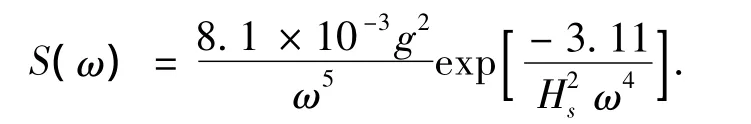
式中:S(ω)表示波谱密度(m2·s);ω是波浪频率(rad/s);Hs是有义波高(m).计算波浪力矩时，在频域范围内将波谱S(ω)分成宽度为δω的N(N=30)个波段，再将每个成分波的力矩累加，可得潜艇受到的瞬时波浪力矩为

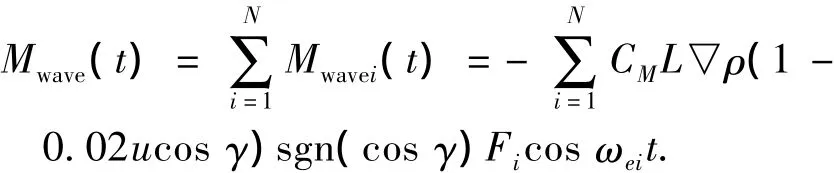
1.3 变结构控制器的设计

1.3.1 航向控制器的设计

将式(3)代入式(2)得无因次潜艇偏航方程如下:

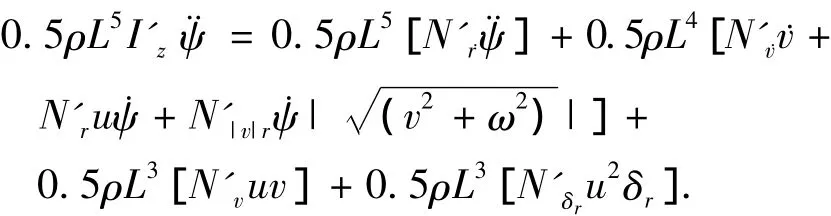
进一步简化得

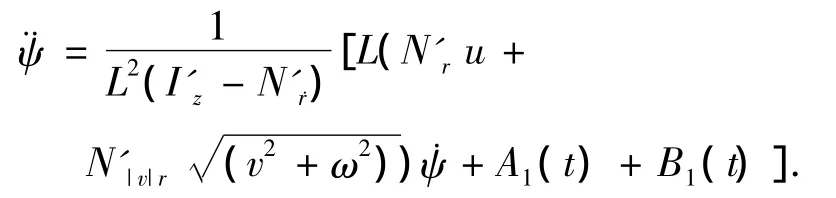
设ψd为给定航向角，ecourse=ψd-ψ(t)为引入的航向角偏差.选择航向变结构控制器切换面:

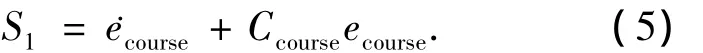
其中:Ccourse是航向切换面中的常数.

选取指数趋近率

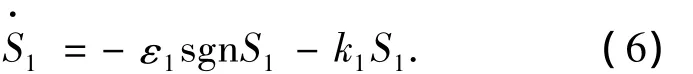
其中:ε1为趋近速度，k1为常数，并有ε1＞0，k1＞0.为减小抖动，可以减小到达S1(X)=0时的速=-ε1;增大k1，减小ε1可以加速趋近过程，减小抖动［9］.对式(5)两边求导数，得

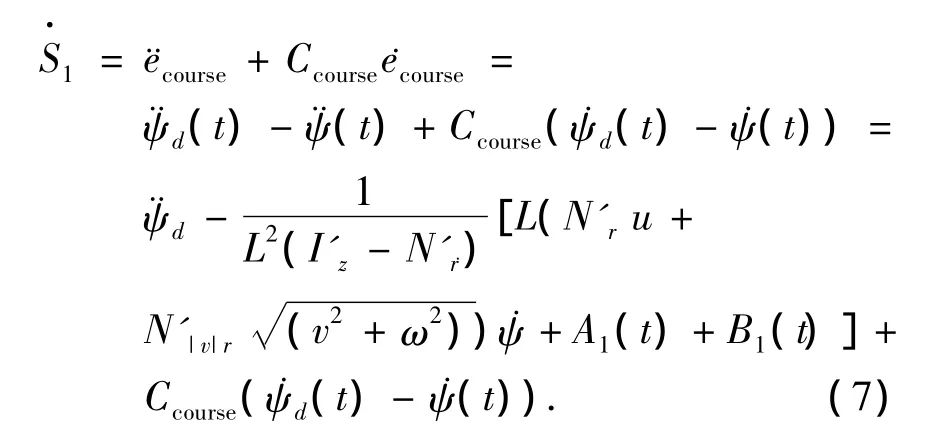
由式(6)，式(7)得航向控制方向舵控制规律为

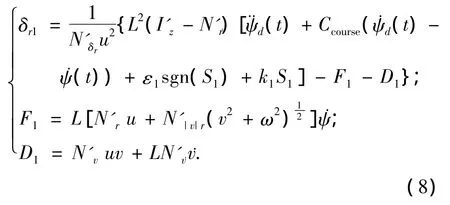
采用光滑函数法来进一步减小变结构控制带来的抖振，取小量正数ε，则式(8)改为

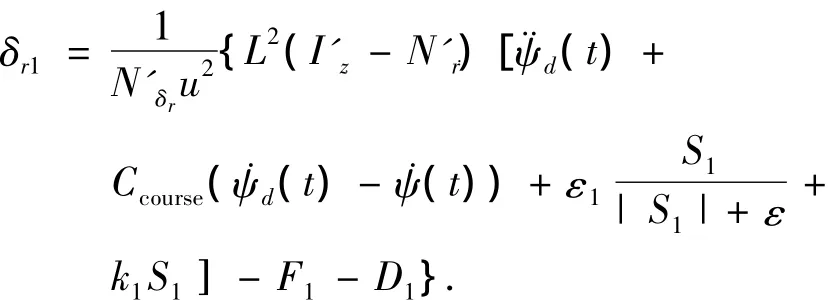
上述过程完成了航向控制器的设计，接下来可以按类似的方法设计出横摇控制器.

1.3.2 横摇控制器的设计

将(4)式代入式(1)得无因次潜艇横摇方程如下:

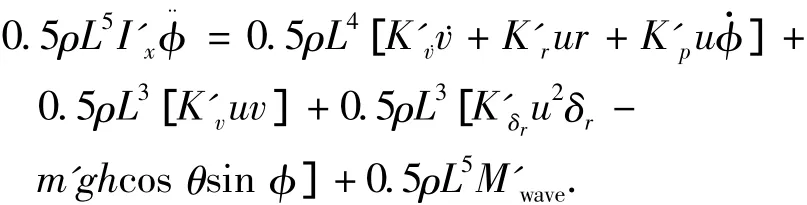
当横摇角很小时，可以近似认为sin φ≈φ，进一步对上面的无因次横摇方程进行简化得

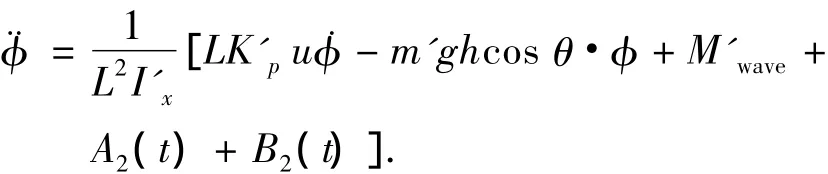
式中:

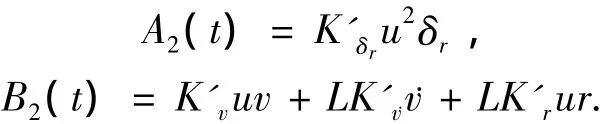
设φd为给定横摇角，eroll=φd-φ(t)为引入的横摇角偏差.选择横摇变结构控制器切换面

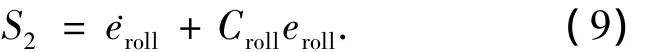
其中:Croll是横摇切换面中的常数.

选取指数趋近率

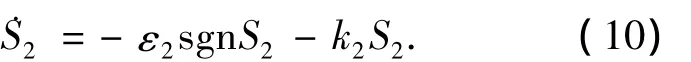
这里ε2为趋近速度，k2为常数，并有ε2＞0，k2＞0.对式(9)两边求导数，得

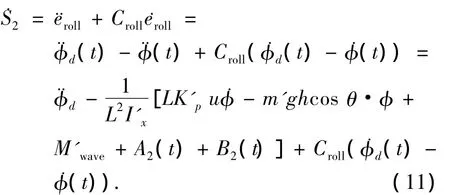
由式(10)，(11)得横摇控制时，方向舵控制规律为

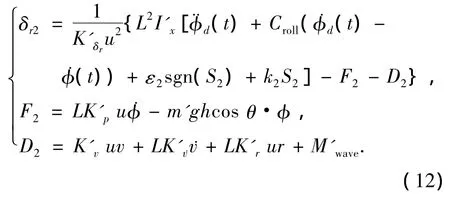
同理，采用光滑函数法对式(12)进行修正，得

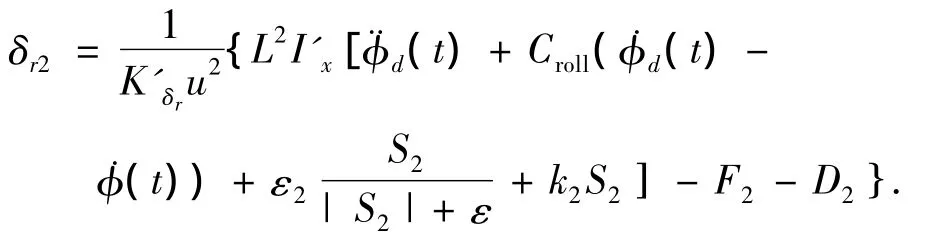
1.3.3 同时对航向、横摇进行变结构控制

通过对航向控制器和横摇控制器的设计，分别得到了控制规律δr1和δr2，综合上述结果，利用加权的方法便得到方向舵总的变结构控制律为

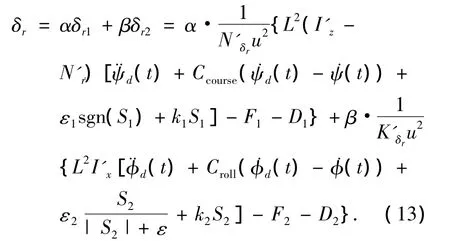
式中:α，β为比例项，一般来说，α，β的值在0～1之间变化.选取比例项的方法通常有两种:一是凭借设计者经验选取;二是根据定深回转过程中及回转结束后横摇角变化的剧烈程度来选α，β.

2 潜艇航向、横摇变结构控制器的改进

变结构控制VSC(Variable Structure Control)的突出优点是对系统参数变化和外界干扰的鲁棒性，而它的明显缺点就是系统存在抖振.当系统参数大范围变化或系统存在较强的不确定性时，必须选择较大的k和ε，才能确保滑动模态存在，而这样又会增大系统的抖振，影响系统的性能.因此，如何根据系统的不确定性和参数变化进行自适应调整，是改进变结构控制器时要研究的一个问题.

近些年来，神经元以其结构简单、自适应、自学习能力强等优良品质引起了研究人员的广泛兴趣［10］.本文在研究了潜艇水平面运动的变结构控制策略后，进一步提出了潜艇自适应神经元变结构控制AVSCT(Adaptive Variable Structure Control with Twin-neuron)的改进方法，原理框图如图1所示.图1中共使用了两个神经元来构成变结构控制系统，其中一个神经元用来调整航向控制器的趋近率参数ε1，另一个神经元用来调整横摇控制器的趋近率参数ε2.采用的控制算法为

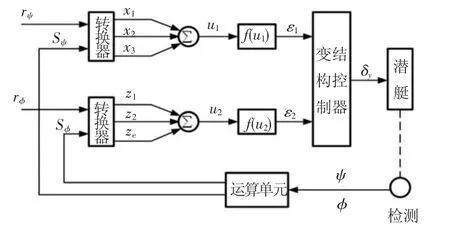
图1 自适应神经元变结构控制系统框图

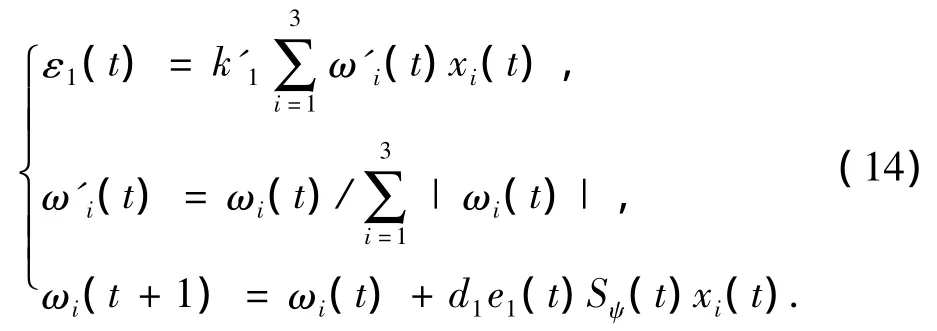
式中:d1＞0为学习速率，ωi(t)为神经元权值，k'1为神经元增益系数，取e1(t)=rψ(t)-Sψ(t)，则神经元输入量为

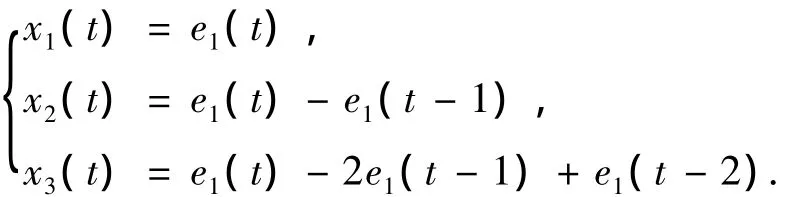
其中，rψ(t)=0为给定的目标函数，Sψ为实际的切换函数.同理

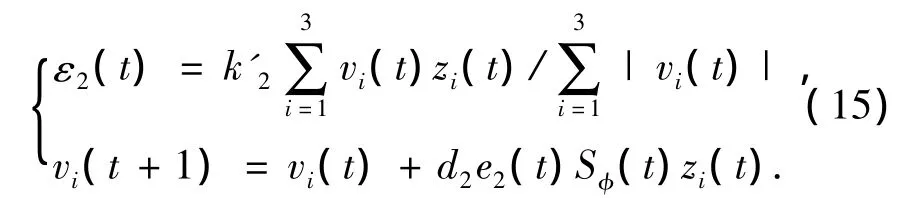
取e2(t)=rφ(t)-Sφ(t)，则神经元输入量为

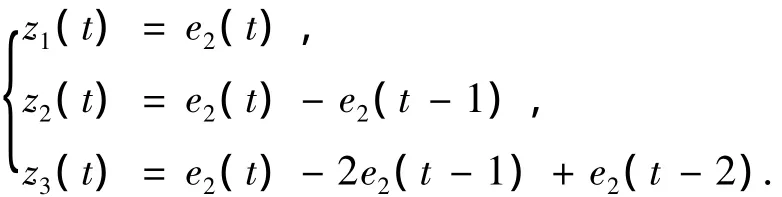
其中:rφ(t)=0为给定的目标函数，Sφ为实际的切换函数，d2＞0为学习速率，vi(t)为神经元权值，k'2为神经元增益系数.图1中的运算单元为

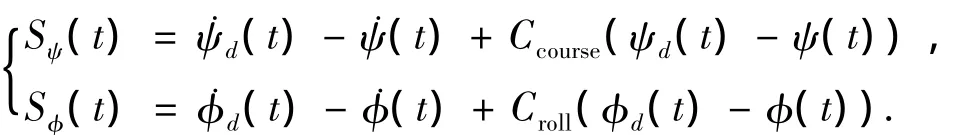
式(13)～(15)组成了具有自适应、自学习、可实时调整参数ε的自适应神经元变结构控制算法.

3 仿真研究

仿真条件是四级海况，有义波高为3 m，采用Pierson-Moskowitz单参数谱，浪向为90°，潜艇在距海面10.5 m处航行，航速为6 kn，指令航向角ψd=60°，指令横摇角 φd=0°，最大舵速为10((°)/s).

3.1 转向过程中，无横摇主动控制

在潜艇转向过程中，未采取横摇主动控制时，α=1，β=0.利用遗传算法，得到此时潜艇方向舵变结构控制器参数.航向控制器参数Ccourse= 0.3，k1=0.7，ε1=0.000 005，ε=0.003 5;横摇控制器参数 Croll= 0.3，k2= 0.6，ε2= 0.000 004，ε=0.003 5.横摇仿真如图2.

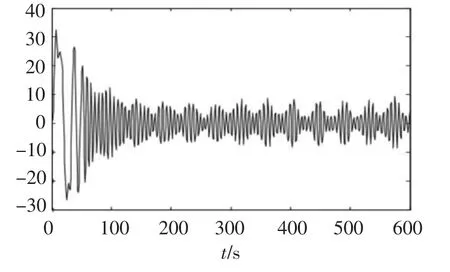
图2 无横摇主动控制时的仿真结果

3.2 转向过程中，采取横摇主动控制

潜艇方向舵变结构控制器参数同3.1节，取α=0.7，β=0.3，即在潜艇转向过程中，加入对横摇的主动控制，潜艇横摇仿真结果如图3所示.

3.3 改进前，对航向、横摇进行的一般变结构控制

取α=0.7，β=0.3，潜艇方向舵变结构控制器参数如下:航向控制器参数Ccourse=0.3，k1= 0.7，ε1=0.5，ε=0.003 5;横摇控制器参数Croll=0.3，k2=0.6，ε2=0.4，ε=0.003 5.横摇仿真结果如图4所示.

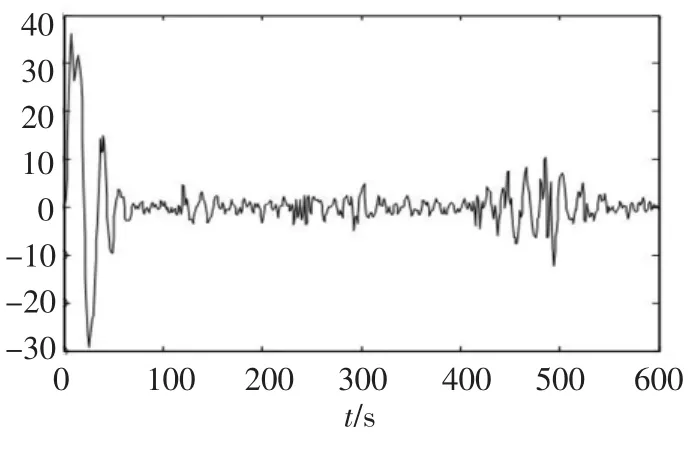
图3 采取横摇主动控制时的仿真结果

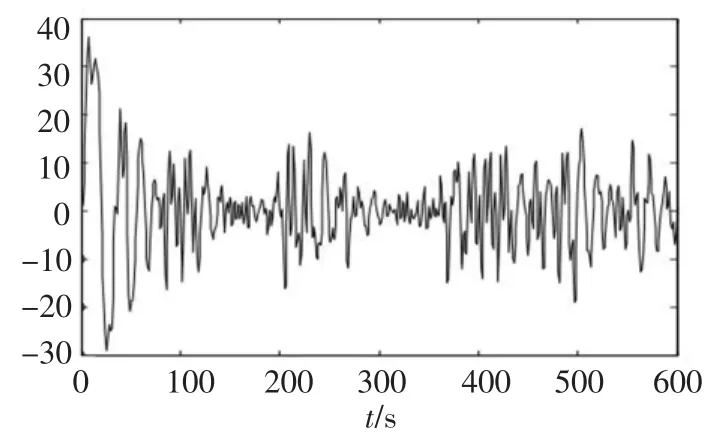
图4 改进前的变结构控制仿真结果

3.4 对航向、横摇进行的自适应神经元变结构控制

取α=0.7，β=0.3，潜艇方向舵变结构控制器参数同3.3节，自适应神经元参数为k'1= k'2=0.5，d1=d2=2，横摇仿真如图5.

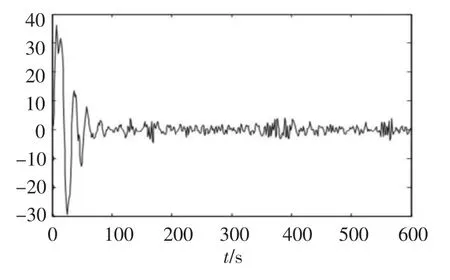
图5 自适应神经元变结构控制仿真结果

4 结论

1)由图2和图3的对比可以看出:加入横摇主动控制后，潜艇在转舵时，横摇角明显减小，这说明所设计的横摇变结构控制器的性能是令人满意的，但是由于采用了舵减横摇的方法，因而该设计存在的缺陷在于航向调节的稳态误差会有所增加.

2)由图4和图5的对比可以看出:采用自适应神经元调整变结构趋近率参数，明显优于改进前的固定趋近率方法.固定趋近率方法对参数变化缺乏自适应性，当系统参数发生变化时，系统性能变差;而本文提出的AVSCT系统，它能根据环境的变化，利用神经元的自学习，在线自适应调整ε1，ε2，与单纯用变结构方法相比，横摇角的稳态误差明显减小，系统抖振的频率也降低了.

［1］ROBERTS G N.Trends in marine control systems［J］. Annual Reviews in Control，2008，32(2):263-269.

［2］冯俊梅，连琏，葛彤.潜艇操纵控制方法的现状与发展［J］.海洋工程，2005，23(1):114-122.

［3］FANG M C，LUO J H.A combined control system with roll reduction and track keeping for the ship moving in waves［J］.Journal of Ship Research，2006，50(4): 344-354.

［4］FANG M C，LUO J H.On the track keeping and roll reduction of the ship in random waves using different sliding mode controllers［J］.Ocean Engineering，2007，34 (3-4):479-488.

［5］FANG M C，LUO J H.The ship track keeping with roll reduction using a multiple-states PD controller on the rudder operation［J］.Marine Technology and SNAME News，2008，45(1):21-27.

［6］MOLLAND A F，TURNOCK S R.Marine rudders and control surfaces:principles，data，design and applications［M］.London:Butterworth-Heinemann，2007.

［7］赵希人，唐慧妍，彭秀艳，等.利用航向舵减横摇控制研究［J］.系统仿真学报，2005，17(1):174-177.

［8］张瑾，连琏，葛彤.潜艇近水面运动鲁棒控制及仿真研究［J］.海洋工程，2006，24(4):32-37.

［9］吴汉松，黄凯，徐袭.舰船航向保持的变结构控制及仿真［J］.海军工程大学学报，2004，16(3):27-32.

［10］ALARCIN F，GULEZ K.Rudder roll stabilization for fishing vessel using neural network approach［J］.O-cean Engineering，2007，34(13):1811-1817.