基于不同航行状态无人艇的水动力模型研究
2010-03-06朱齐丹刘志林于瑞亭
陈 铭 朱齐丹 刘志林 于瑞亭
哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001
基于不同航行状态无人艇的水动力模型研究
陈 铭 朱齐丹 刘志林 于瑞亭
哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001
无人艇操纵灵活,机动性强,在很多方面都有着广泛的应用。但相关研究还比较少。以往的单一水动力模型只是针对特定航行状态进行研究,对于不同的航速,单一的水动力模型已不再适用。因此随着航速不同,建立同一艘无人艇在不同航行状态下的水动力模型,并研究在此模型下无人艇的运动特性成为一个难点,也是研究真实无人艇的一个关键环节。论文在以往学者的研究成果基础上,给出了一种全新的水动力模型,并就某一真实无人艇,研究从静止到高速起滑整个过程的水动力与航速之间的开环变化关系。仿真结果表明了所给模型的有效性。
无人艇;航行状态;水动力模型;操纵性
1 引言
无人艇的研究始于20世纪末21世纪初,成为现在研究的一大热点。文献[1]针对高性能槽道无人艇的运动特性进行过研究;文献[2]针对低速排水型无人艇的水动力模型进行过总结;文献[3]用神经网络的方法针对高速无人艇进行过水动力与航速关系的离散拟合;文献[4]针对高速喷水推进无人艇进行过设计处理;另外,文献[5]针对一些类型的高性能水面艇的水动力计算进行过讨论。
这些研究的共同点是:1)都是只针对排水,半排水,或滑行状态中单一航行状态水动力模型的无人艇研究;2)未进行过开环运动特性的分析;3)未将不同航行状态的水动力模型应用于同一艘无人艇上。而随着航速的增加,无人艇水动力模型随航速不同而变化[6],所以将单一的水动力模型应用于同一艘无人艇的研究不能准确地反映无人艇真实的状态,具有一定的局限性。
本文将不同航速下的水动力模型加以归纳和推导,得出不同航行状态的水动力模型,针对纵向水动力模型进行研究,并将不同航行状态的纵向水动力模型应用于某一真实无人艇,最后给出纵向速度和纵向水动力随时间的开环变化关系,进而得到纵向水动力随航速的开环变化关系,可应用于真实的无人艇纵向水动力研究及真实艇体参数设计研究中。
2 动力学模型分析
无人艇在排水量一定的情况下,随着速度的增加,其航行状态相应改变:低速时为排水状态;中速时为过渡状态(半排水状态);高速时为滑行状态。不同航行状态下,沿航行方向上的水动力即纵向水动力各不相同,以往的排水型艇的纵向水动力模型随着航速的增加已不再适用。
当艇进入半排水状态后,随着航速的增加,艇首逐渐抬起,摩擦阻力正比地随浸湿面积的减小而减小,此时无人艇水动力的急剧增加主要是由于喷溅阻力和兴波阻力的增加引起的。半排水状态的水动力曲线呈驼峰型,处在水动力峰值区域航行对艇不利,对动力装置和推进器的运行也会带来不利影响。当运动速度达到容积傅汝德数大于3时,艇首抬出水面并开始滑行,艉纵倾减小,水动力越过峰值后迅速下降,这是因为除摩擦力减小外,兴波阻力也减小了。
滑行状态是指艇越过起飞水动力峰后的航行状态。此时,艇的部分重量依靠艇底水流产生的流体动举力来支撑,排水体积产生的浮力所占比例较排水和半排水状态小。对滑行状态来说,其速度有一个下限,用容积傅汝德数来衡量,当傅汝德数大于3时,艇就已经进入滑行状态了[5]。
本研究采用的是喷水推进艇型,在平野模型[2]的基础上结合喷水推进的特性以及海浪干扰建立四自由度船舶运动数学模型。因此本文讨论的无人艇运动模型采用平野模型中关于船舶姿态和轨迹的运动学方程,得到如下方程:
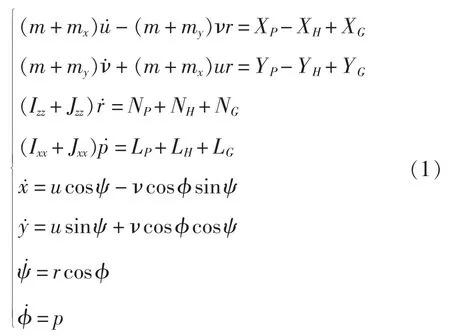
式中,XP,YP,NP,LP为推力和推力力矩;XH,YH,NH,LH为水动力和水动力力矩;XG,YG,NG,LG为环境干扰力及力矩;m 为艇的质量;mx,my,Jzz分别为艇的附加质量和附加惯性矩;Ixx+Jxx为横摇附加惯性矩;u,ν分别为艇的纵向速度和横向速度;r,p分别为艇的转向角速度,横摇角速度;ψ,φ分别为艇的首摇角和横摇角;x,y分别为艇的纵向位移和横向位移。
3 无人艇纵向水动力理论模型

1)排水航行状态:当 0≤FrΔ≤1,为排水状态[5]。此时航速比较低,纵向水动力所占比例较小,艇基本上由静浮力支持。在此状态下,把受横向及回转运动影响的水动力简化成ν、r交叉耦合项,用如下公式:
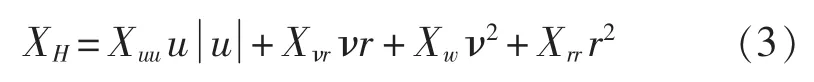
其他纵向水动力导数的方法计算如下。
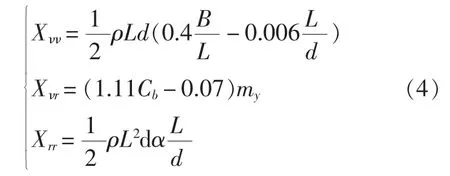
其中,α 为一个系数,通常取 0.0005[2-3];Cb为艇的方形系数;d为艇的平均吃水深度。
本论文研究的是没有转向情况下的纵向水动力,所以ν=0,r=0,此时航速将ν =0,r=0 代入式(2-2),结合式(2)、式(3),得到结果如下。


式中,Ct=Cf+Cr+ΔC +Ca+Cap为总阻力系数;Ca为附体阻力系数;Cap为空气系数;Ct大小的确定详见文献[5]。
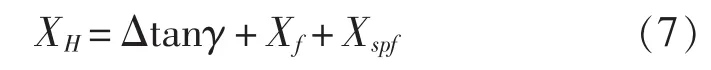
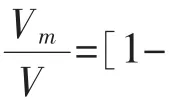
综合以上分析,得到无人艇不同航行状态纵向水动力方程为:

式中,XHL为低速排水状态时的纵向水动力;XHM为中速半排水状态时的水动力,XHH为高速滑行状态时的水动力。
4 仿真实验研究
文献[4]研究了一种水面滑行艇,其具体参数如表1所示。纵向水动力模型用最终推导出的式(8)。

表1 艇的基本参数
在仿真过程中,有些参数是随艇的状态变化的,由于变化量微小,而且对仿真结果影响甚微,故在误差允许范围内均设定为定值,这些参数具体为:Cf= 0.002 4,ΔC = 0.000 5,Cr= 0.004 1,Ca=0.000 9,Cap= 0.000 9,l= 2.5 m,β = 10.4°,γ = 7.5°,ρ=1 000 kg/m3,Δλ =0.1 m。
由上得 Ct=Cf+Cr+ ΔC +Ca+Cap=0.008 8,由表 1 得到 λ=l/B=0.794;而且未考虑海面波浪干扰,即在静海面进行的仿真研究。
排水和半排水状态时,由于艇在静水面悬浮,大部分重量由浮力来支撑,故仿真过程中取排水量 Δ 等于艇的质量m,即Δ=6 700 kgΔ。 由式(2)和表1可以得到排水和半排水状态时 =Δ/ρ=6.7 m3;而滑行状态则不然,浮力所占比例较排水和半排水状态小,故本研究中取=0.85 m3,故由式(2)得到滑行状态的排水体积== 5.695 m3。
仿真分别研究无人艇由静止到高速起滑整个过程的开环纵向速度和纵向水动力随时间变化的关系,因此得到纵向水动力随纵向速度的变化关系。具体如实验1和实验2,实验仿真验证如实验3。
实验1:纵向速度u随时间t开环变化规律仿真,如图1所示(图中dewatering表示排水状态;transiting表示过渡状态 (半排水状态);sliding表示滑行状态)。

实验2:不同航行状态下纵向水动力与时间开环变化关系仿真,如图2;不同航行状态下纵向水动力随纵向速度开环变化关系仿真,如图3。图中纵坐标中出现的N表示牛顿。同时,图3中根据上述推导出的速度范围分别标出了排水、半排水和滑行状态的转折航速。

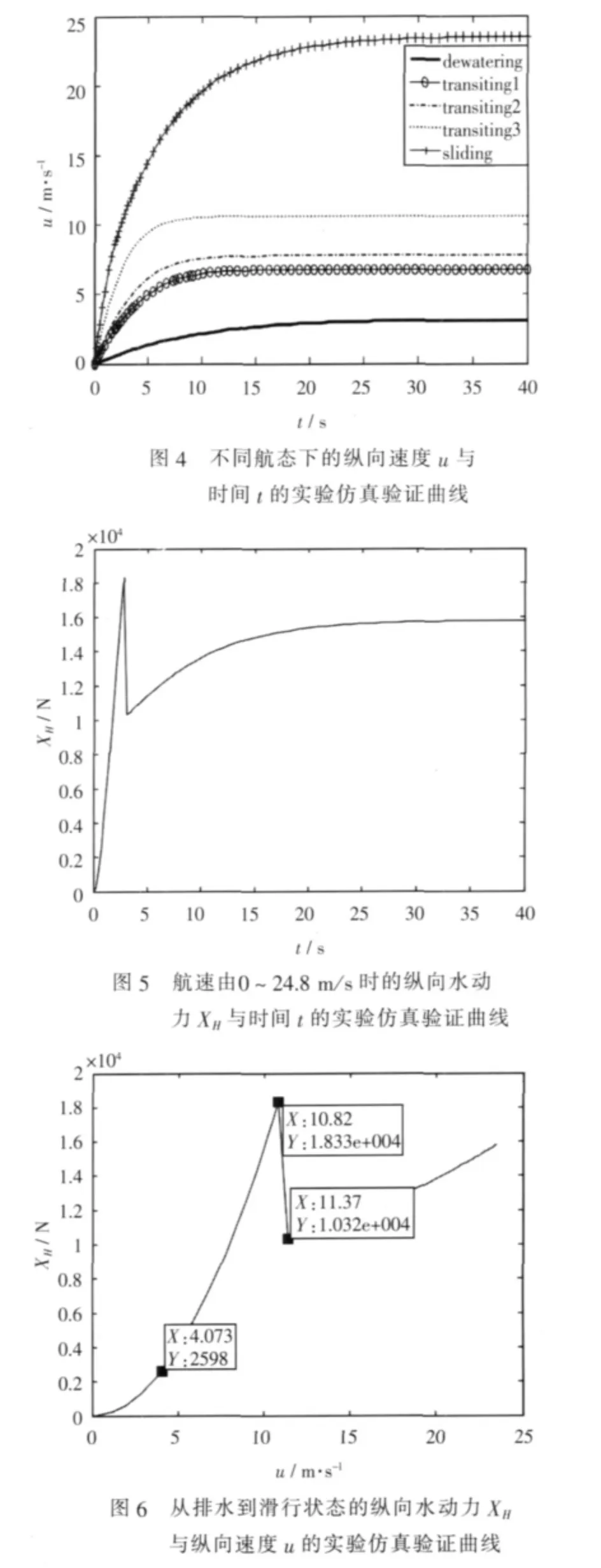
实验3均在无人艇初始静止,且打了一个20°的舵角时进行的实验仿真验证,纵向速度u随时间t开环变化规律,不同航行状态下纵向水动力与时间开环变化关系和不同航行状态下纵向水动力随纵向速度开环变化关系实验仿真验证结果分别如图4~图6。
5 仿真结果分析
实验1 分析图1:同样的喷水推进器,纵向速度随所输入的功率增大而增大,纵向水动力随纵向速度增大而增大,但喷水推力随纵向速度增大而减小[8-9],直至纵向推力和纵向水动力相等时,纵向合外力为零,纵向速度达到稳定。
实验2 分析图2:纵向水动力随纵向速度增加而增加,但是不同航速下的纵向水动力模型是不同的,排水状态下的纵向水动力较小,因为排水状态较半排水状态航速较小;在半排水状态下,纵向水动力随纵向速度增大而增大,是排水、半排水和滑行3个状态中最大的;当航速达到稳定时,纵向水动力恒定。
分析图3:由于艇的参数选取适当,将排水状态和滑行状态之间的过渡状态,即半排水状态的速度范围限定在了一个较小范围内,既缩短了过渡时间,又避免了半排水状态的较大水动力对艇的影响。在半排水状态下,即使输入很高的功率,也难以获得较高航速,这样会降低艇的效能,故要尽快过渡到滑行状态。进入滑行状态,艇的纵向水动力比半排水状态的小得多,故纵向水动力突然降低,但由于半排水状态和滑行状态的航速范围有重叠,故图3中排水状态和滑行状态的切换不是瞬间达成的,而是经历了一个微小的航速变化后达到滑行状态的。在滑行状态,虽然纵向水动力仍随纵向速度增加而增加,但较半排水状态的水动力峰值下降很多,直至航速达到稳定并足够大时,此阶段的水动力最终会超过在半排水状态时的水动力峰值,根据图3的变化趋势,航速约达到40 m/s时,滑行状态下的水动力开始超过半排水状态的水动力峰值,但这速度对一般的无人艇来说很难达到。总的来说,随着航速的增加,纵向水动力增加,基本符合理论[10]变化趋势。(本研究中未标注单位的均为国际标准单位。)
通过实验3与实验1和实验2对比可见,在误差允许的范围内,本文提出的无人艇纵向水动力模型的仿真结果基本符合实验验证结果,因此本文提出的无人艇纵向水动力模型是可靠的。而且经本实验可知,以往单一的水动力模型均是采用排水阶段纵向水动力模型(见式(8)的第一行)或滑行阶段的纵向水动力模型(见式(8)的第三行),不论用哪种模型,纵向水动力随航速和时间都是全程单调递增的 (如图6的第一段或第三段曲线),与前述实际情况不符,不能准确真实地反映出无人艇在海面航行时纵向水动力变化情况。
6 结束语
本文对无人艇在排水、半排水和滑行等状态下的运动特性进行分析,并把不同航速下的纵向水动力模型应用于真实无人艇,得到开环纵向速度和纵向水动力随时间变化的关系。比以往采用单一水动力模型应用于无人艇的分析有了改进,对无人艇运动状态分析更接近于真实的航行状态。本研究总结推导的不同航行状态的纵向水动力模型为真实艇的纵向水动力研究及真实艇的总体设计提供了一定的理论参考依据。
[1]苏永昌,赵连恩.高性能槽道滑行艇的运动特性[J].中国造船,1996(1):11-16.
[2]KIJIMA K,KATSUNO T,NAKIRI Y,et al.On the maneuvering performance of a ship with the parameter of loading condition[J].日本造船学会论文集,1990(168):141-148.
[3]高双,朱齐丹,李磊.基于神经网络的高速无人艇模糊PID 控制[J].系统仿真学报,2007,19(4):776-779.
[4]沈奉海,梁仲德,周亿洪,等.高速喷水推进滑行艇处理[J].舰船科学技术,1982(6):62-65.
[5]赵连恩,韩瑞峰.高性能船舶水动力原理与设计[M].哈尔滨:哈尔滨工程大学出版社,2007.
[6]ZHANG Y,WEN C,SOH Y C.Adaptive back stepping control design for systems with unknown high-frequency gain[J].IEEE Trans on Automatic Control,2000,45(12):2250-2254.
[7]朱珉虎.滑行艇水动力计算[J].船舶工业技术经济信息,2005(2):30-33.
[8]金平仲.船舶喷水推进[M].北京:国防工业出版社,1986.
[9]ALLISON J,BECNEL A,PURNELL J.Unified propulsion package for the very high speed sealift trimaran (VHSST)design application [C]//Symposium of Waterjet Propulsion III.RINA, 2001.
[10] AHMED M S.Neural-net based direct adaptive control for a class of nonlinear plants on Neural Networks [J].IEEE Trans.2000,45(1):119-124.
Hydrodynamic Modeling of Unmanned Surface Vehicle in Different Sailing Conditions
Chen Ming Zhu Qi-dan Liu Zhi-lin Yu Rui-ting
College of Automation,Harbin Engineering University,Harbin 150001,China
The Unmanned Surface Vehicle (USV) can be easily manipulated and maneuvered and has been extensively used for both military and commercial application.However, the hydrodynamic modeling of USV was rarely researched,the single hydrodynamic models previously employed in the related literature were merely designed for specific sailing condition.USV's sailing status will change with the variation of speed, so the single hydrodynamic model is not acceptable all the time.The establishment of hydrodynamic models in different sailing conditions for various speeds and analyzing motion features of USV based on these models are necessary and of particular interest in this area.A new hydrodynamic model according to the results of related literature was rebuilt.The open-loop concern of hydrodynamic performance with speed from zero to high-speed sliding was studied with a real USV.The results of simulation show that the hydrodynamic models proposed are better than the single hydrodynamic models.
USV; sailing condition; hydrodynamic model; maneuverability
TN911.6
A
1673-3185(2010)06-01-05
10.3969/j.issn.1673-3185.2010.06.001
2010-03-15
国家自然科学基金资助项目(50909026),中国博士后科学基金资助项目(20090450949)
陈 铭(1985-),男,博士研究生。研究方向:控制理论与控制工程。E-mail:chenmingb09@ hrbeu.edu.cn
朱齐丹(1963-),男,教授,博士生导师。研究方向:控制理论与控制工程
