水下结构物舱壁振动控制的结构参数优化研究

刘监波 刘文玺 周其斗 吴崇健 徐志云

1中国舰船研究设计中心，湖北武汉 430064

2海军工程大学 船舶与动力学院，湖北 武汉 430033

水下结构物舱壁振动控制的结构参数优化研究

刘监波1刘文玺2周其斗2吴崇健1徐志云1

1中国舰船研究设计中心，湖北武汉 430064

2海军工程大学 船舶与动力学院，湖北 武汉 430033

舱壁结构参数选择对舱壁振动性能有直接影响。为减小舱壁振动，采用有限元法，选择舱壁板厚度、加强筋数量、加强筋截面大小为变化的结构参数，分析振动随激振力频率、激振力作用方向、舱壁结构参数的变化规律，得到在动载荷作用下，舱壁振动的均方法向速度频响曲线，并以此为依据，设计了潜艇舱壁的结构形式和结构参数。优化的结果可以为舱壁结构参数选择提供理论依据。

振动；结构设计；均方法向速度；结构参数

1 引言

研究舱壁等弹性结构的振动指标随结构参数的变化规律，是结构降噪设计和结构声学优化的重要内容之一，一般对水中兵器和舰船隐身具有十分重要的意义。对于复杂的弹性结构的振动问题，采用数值计算方法进行分析。通用、有效的数值方法是有限元法［1］、有限元 ／边界元耦合法［2］。 文献［3］对船舶上层建筑整体振动有限元建模方法进行研究，讨论了不同计算模型、边界条件、附加水质量以及装载情况对上层建筑整体振动固有频率的影响。文献［4］利用耦合的有限元／边界元法分析了复合材料板在谐频和随机激振力作用下的响应特性。文献［5］采用耦合的有限元／边界元法对双层加筋柱壳在单点和两点随机激振力作用下的振动进行了数值仿真和实验测试，显示了该方法的优越性。文献［6］利用有限元法、有限元／边界元法耦合法计算了带有舵翼结构的水下航行器尾部结构模型的动态特性，与实验结果的比较表明了该方法的有效性。文献［7］利用有限元法，研究了水下结构物舱段的结构振动响应对双层隔振系统主要设计参数的灵敏度，从而为结构的优化设计和模型修正提供理论基础。

上述研究给出了较好的预报结果，但大多都是对某一结构进行研究，系统地对舱壁结构的振动指标随结构参数的变化规律进行研究的较少。本文研究单舱壁结构在空气中的振动性能，因此采用有限元法，选择舱壁板厚度、加强筋数量、加强筋截面大小为变化的结构参数，得到了在动载荷作用下，舱壁振动的均方法向速度频响曲线，分析总结了各种参数对舱壁振动的影响规律，给出了某水下结构物舱壁结构的设计方案。

2 结构振动分析的理论公式

2.1 结构动力响应

采用有限元法，对结构进行动力响应分析，方程为：

式中，［M］为质量矩阵；［C］为阻尼矩阵；［K］为刚度矩阵；｛δ｝为节点位移；｛δ˙｝为节点速度；｛δ¨｝为节点加速度；｛F｝为节点载荷。

给定结构的边界条件，求解式（1），得到结构节点处的位移、速度和加速度。

2.2 均方法向速度

为了衡量舱壁的振动性能，采用表面均方法向速度作为主要衡量指标，计算公式为：

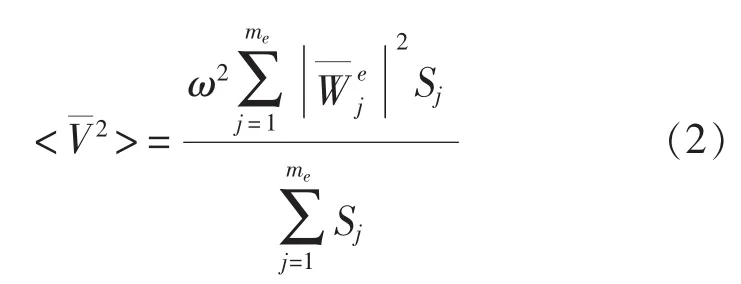
3 舱壁振动响应数值计算

3.1 舱壁约束边界的处理

舱壁结构实际上是作为一个部件与整艇相连，舱壁的振动与整艇其他部分的振动是相互耦合的，即舱壁的振动会传递到该舱壁以外的其他部分，其他部分的振动也会传递到该舱壁上，从而相互影响。

目前，对舱壁结构振动边界的处理没有规范性的方法，多数文献用弹簧模拟，但对弹簧参数的确定没有比较统一的合适方法，为了尽可能考虑所研究的舱壁与其他部分的相互影响，根据舱壁的实际位置，创建了合适的舱段模型作为舱壁的边界，将舱壁安装在舱段中间，动载荷大小为1 N，作用在加强筋上，频率范围从10～300 Hz，间隔是1 Hz，计算模型如图1所示。

3.2 舱壁板厚度对舱壁结构振动的影响

以舱壁板厚度为变化参数，计算舱壁振动的均方法向速度，板厚取10 mm～30 mm，以5 mm为间隔，结果如图2～图3所示，图2是动载荷沿纵向的计算结果，图3是动载荷沿垂向的计算结果，根据图2得到板厚不同时均方法向速度峰值出现的频率点和峰值大小，将最大峰值频率及最大峰值、10 Hz和20 Hz后第一个峰值频率和峰值列出，如表1所示。由图2可以看出，当动载荷沿纵向时，以15 mm板厚为分界点，均方法向速度峰值随板厚增加呈先增大后减小的趋势；整体上，峰值数量随板厚增加而减少，峰值分布的频率范围明显减小。

表1 板厚不同时均方法向速度峰值（纵向力）

根据图3得到板厚不同时均方法向速度峰值出现的频率点和峰值大小，将最大峰值频率及最大峰值、10 Hz和20 Hz后第一个峰值频率和峰值列出，如表2所示。由图3可以看出，整体上，随板厚增加峰值大小呈减小趋势，峰值数量明显减少，且分布在较小的频率范围内，与激励纵向作用时的规律一致。

表2 板厚不同时均方法向速度峰值（垂向力）

3.3 加强筋数量对舱壁结构振动的影响

以加强筋数量为变化参数，计算舱壁振动的均方法向速度，加强筋数量分别取7、11、15、21，间距分别是 1.163 m、0.775 m、0.581 m、0.422 m，结果如图4、图5所示，图4是动载荷沿纵向的计算结果，图5是动载荷沿竖向的计算结果，根据图4，得到加强筋数量不同时均方法向速度峰值出现的频率点和峰值大小，将最大峰值频率及最大峰值、10 Hz和20 Hz后第一个峰值频率和峰值列出，如表3所示。由图4可以看出，当动载荷沿纵向时，以加强筋数15根为分界点，均方法向速度峰值随加强筋数量增加呈先增大后减小的趋势；整体上，均方法向速度峰值主要分布在150 Hz以下。

表3 加强筋数量不同时的均方法向速度峰值（纵向力）

根据图5得到加强筋数量不同时均方法向速度峰值出现的频率点和峰值大小，将最大峰值频率及最大峰值、10 Hz和20 Hz后第一个峰值频率和峰值列出，如表4所示。由图5可以看出，当动载荷沿垂向时，均方法向速度峰值随加强筋数量增加呈减小的趋势；峰值点分布的频率范围随加强筋数量增加呈减小趋势，峰值点向高频移动。

因此，在确定舱壁加强筋数量时，要综合考虑载荷作用方向、载荷频率范围、舱壁重量等各方面因素。

3.4 加强筋截面对舱壁结构振动的影响

以加强筋截面为变化参数，计算舱壁振动的均方法向速度，取一较小截面尺寸为基础尺寸，其余3种尺寸是在基础尺寸基础上分别增加10%、20%、30%，结果如图6、图7所示，图6是动载荷沿纵向的计算结果，图7是动载荷沿竖向的计算结果。根据图6，得到加强筋截面大小不同时均方法向速度峰值出现的频率点和峰值大小，将最大峰值频率及最大峰值、10 Hz和20 Hz后第一个峰值频率和峰值列出，如表5所示。由图6可以看出，整体上，均方法向速度峰值随加强筋截面尺寸增加呈明显的减小趋势，且峰值点主要分布在250 Hz以下。

表4 加强筋数量不同时均方法向速度峰值（垂向力）

根据图7，得到加强筋截面大小不同时均方法向速度峰值出现的频率点和峰值大小，将最大峰值频率及最大峰值、10Hz和20Hz后第一个峰值频率和峰值列出，如表6所示。由图7可以看出，当动载荷沿垂向时，均方法向速度峰值随截面尺寸的增加呈明显减小的趋势，峰值的数量呈减小趋势，且分布在较窄的频率范围内。

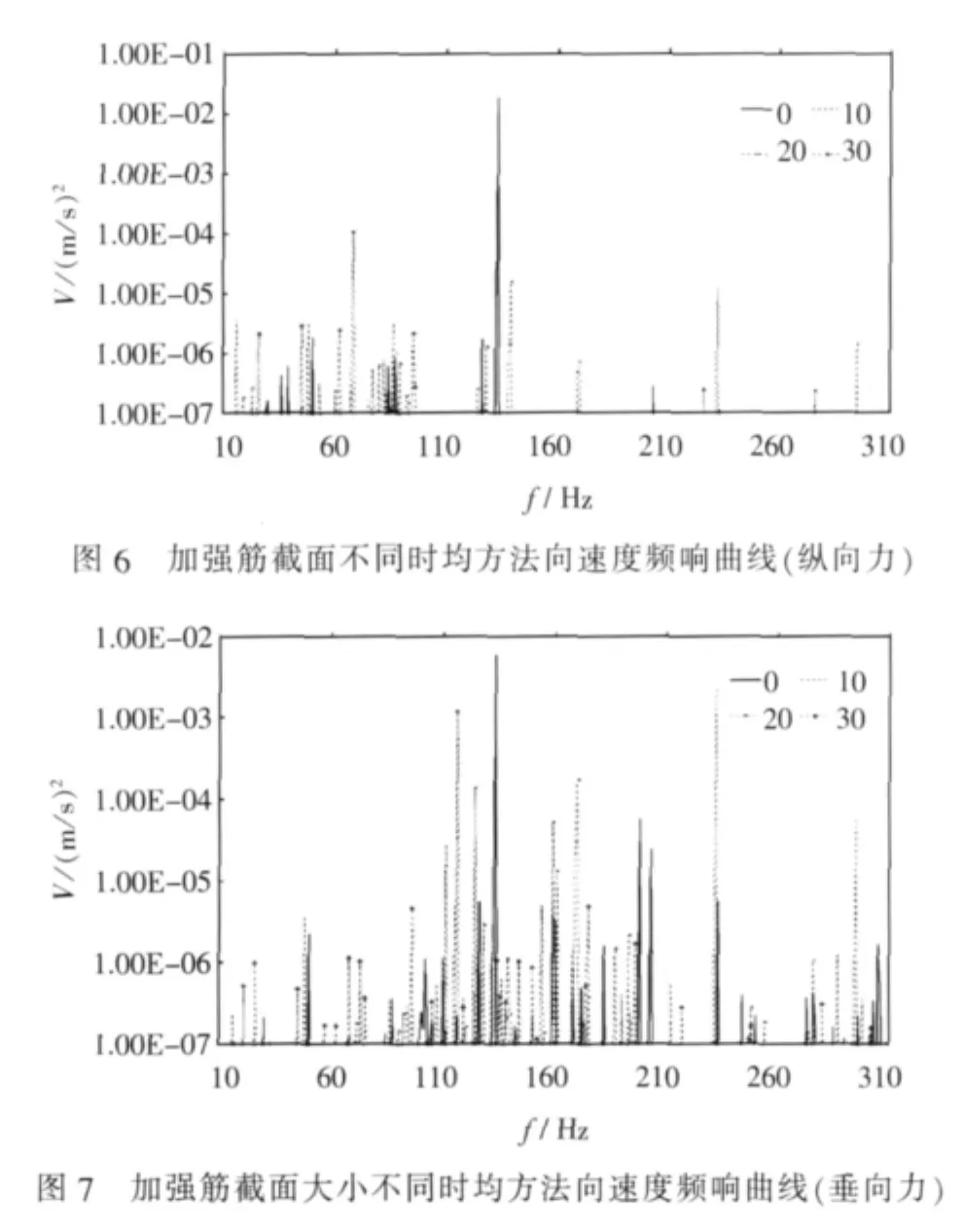
表5 加强筋截面不同时均方法向速度峰值（纵向力）

表6 加强筋截面不同时均方法向速度峰值（垂向力）

3.5 舱壁设计

以 3.2～3.4 节的结论为依据，设计舱壁结构。

要设计的舱壁属于强舱壁，位于水下结构物耐压壳体部分两舱段的连接处，其中一舱的水平横梁上安放设备基座，因此，舱壁主要受到垂向周期性激振力的作用，激振力的频率在300 Hz以下，同时考虑到重量和强度方面的要求，横向加强筋中，有3根较大的加强材，垂向加强筋是13根，舱壁板厚取22 mm，加强筋截面取较大的尺寸，设计的舱壁结构如图8所示。

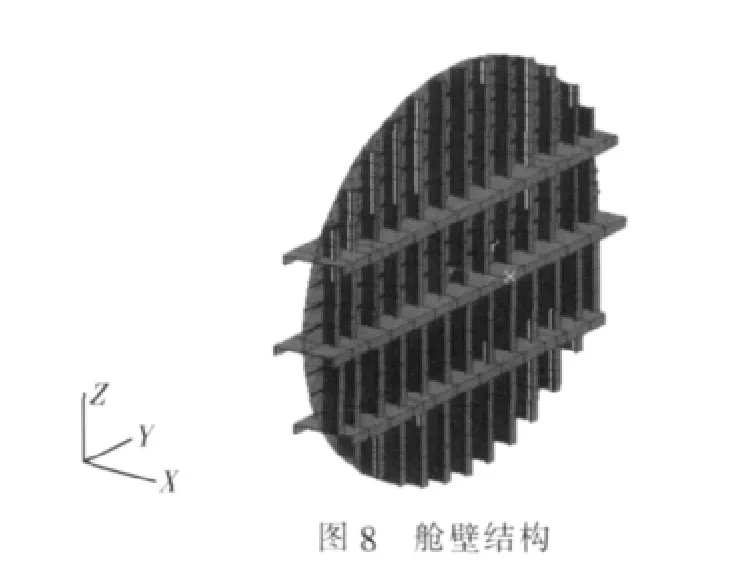
在上述结构中，横向的3根加强筋可以在两侧分别用角钢模拟，也可以用在舱壁与横向加强筋的连接方式上采用2种方式：1）舱壁两面分别焊接角钢；2）舱壁分3段与横向加强筋焊接，采用有限元分别针对两种结构形式进行计算，结果如图9、图10所示。它们分别是动载荷沿纵向和垂向作用时舱壁振动的均方法向速度频响曲线，可以看出，用角钢，峰值比槽钢的小很多，且峰值分布在较小的频率范围内，因此采用角钢对舱壁进行加强的方式较为合理。根据图9和图10，得到设计舱壁均方法向速度峰值出现的频率点和峰值大小，将最大峰值频率及最大峰值、10 Hz和20 Hz后第一个峰值频率和峰值列出，如表7所示。

为了能够更清楚地看出设计舱壁振动性能的优劣，从结构参数对结构振动灵敏程度的角度进行说明。为了衡量结构参数对结构振动的灵敏程度，采用均方法向速度频率曲线作为基本依据，并以均方法向速度的频率曲线在一定频率段下围出的面积作为振动特性的另一标准。如果某结构参数的均方法向速度频率曲线在一定频率段下的面积大，则相应的结构振动大，反之则结构振动小。

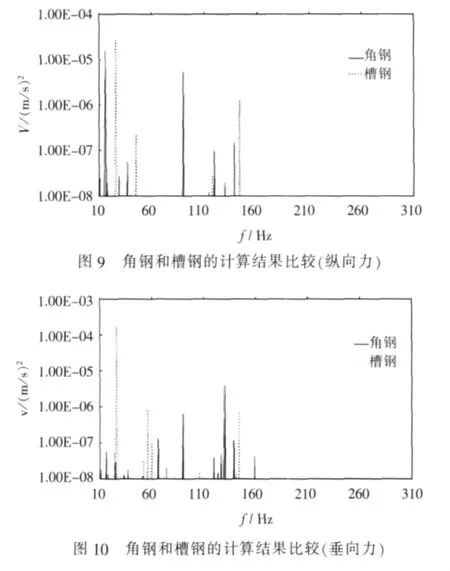
表7 设计舱壁的均方法向速度峰值

设计舱壁在10～300 Hz频率范围内均方法向速度频率曲线下的面积为 A0，3.2 ～3.4 节中的其中一种结构形式舱壁，其相应频率曲线下的面积为A1，则只改变一种结构参数的舱壁比设计舱壁的均方法向速度在10～300 Hz频率范围高出的分贝数为 lg（A1／A0）。

表8～表10分别是取不同板厚、加强筋数量、加强筋截面尺寸时，lg（A1／A0）的计算结果，表中数值为正的代表增大，数值为负的表示减小，从表8～表10的计算结果可以看出，按上述方法设计出的舱壁，振动性能良好。

4 结论

1）可以根据舱壁振动响应随板厚不同的变化规律，为舱壁选择合适的板厚。

2）为得到较好振动性能的舱壁，在确定舱壁加强筋数量时，要综合考虑载荷作用方向、载荷频率范围、舱壁重量等各方面的因素。

表 8 板厚不同时的 lg（A1／A0）

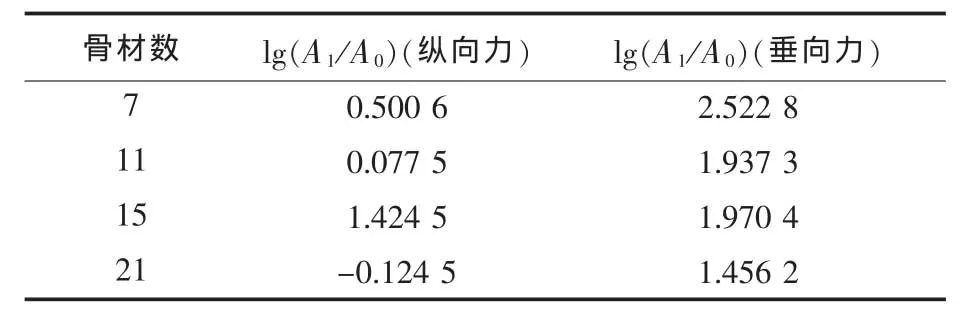
表9 加强筋数不同时的lg（A1／A0）

表10 加强筋截面不同时的lg（A1／A0）

3）选取大截面的加强筋，有利于舱壁振动的减弱。

4）以上述3点结论为依据，尽可能选取最优的结构参数，可以设计出振动性能良好的舱壁。

［1］金咸定，赵德有.船体振动学［M］.上海：上海交通大学出版社，2000.

［2］ZHOU Q D，JOSEPH P F.A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure［J］.Journal of Sound and Vibration， 2005， 283（3－5）：853－873.

［3］殷玉梅，赵德有.船舶上层建筑整体振动有限元建模方法研究［J］.中国造船，2009，50（3）：49－56.

［4］MEI C，SHIRAHATTI U.Coupled boundary／finite element methods for random structral－acoustic interaction problem［R］.Norfolk：AIAA，1995.

［5］纪纲.充水双层柱壳声辐射实验研究［D］.武汉：海军工程大学，2004.

［6］TONG Z， ZHANG Y，ZHANG Z，et al.Dynamic behavior and sound transmission analysis of a fluid－structure coupled system using the direct－BEM／FEM ［J］.Jounal of Sound and Vibration， 2007，229（3）：645－655.

［7］邹春平.船舶结构振动响应灵敏度分析［J］.中国舰船研究，2006，1（2）：26－31.

Optimal Parametric Design of Bulkhead Vibration Control for Underwater Structure

Liu Jian－bo1 Liu Wen－xi2 Zhou Qi－dou2Wu Chong－jian1 Xu Zhi-yun1
1 China Ship Development and Design Center， Wuhan 430064， China
2 College of Naval Architecture and Power， Naval University of Engineering， Wuhan 430033， China

The approach of structural parameter selection may have obvious impact on the vibration characteristics of bulkheads of underwater structure.For purpose of reducing the structural vibration，variations of bulkhead plate thickness， numbers and cross－sections of reinforced rib were investigated numerically by the Finite Element Method （FEM）.On that basis， various characteristics changing with the vibration frequency－response， direction of excited force and structural parameters were analyzed，and the results of mean square normal velocity versus frequency－response subjected to dynamic loads were obtained.This research provides a basis for parameter selection and structural configuration in the design of similar bulkheads.

vibration； structural design； mean square normal velocity； structure parameter

U661.44

A

1673－3185（2010）06－21－05

10.3969/j.issn.1673-3185.2010.06.005

2010-07-20

刘监波（1973－），男，博士研究生。研究方向：减振降噪。E-mail：wangxia@csoc.cn

吴崇健（1960－），男，研究员，博士生导师。研究方向：噪声与振动控制。E-mail：wcj2002@163.com