改进遗传算法在驳船配载中的应用
2010-03-06夏华波纪卓尚张明霞
夏华波 纪卓尚 张明霞
大连理工大学船舶工程学院,辽宁大连 116024
改进遗传算法在驳船配载中的应用
夏华波 纪卓尚 张明霞
大连理工大学船舶工程学院,辽宁大连 116024
驳船是大型海洋结构物下水作业的一种常用运输工具。驳船的配载主要是依据静力学平衡原理和船舶基本知识对船舶浮态的调节。为了在较短时间内完成配载作业,对遗传算法进行了改进,提出种群全部交叉和分布式动态惩罚函数法等改进机制,对驳船配载中的调载水量分布进行优化。计算结果表明,改进遗传算法的配载方案比基本配载方案时间更短、效率更高。运用本改进遗传算法对驳船配载进行方案优化,能够满足工程要求,缩短上驳作业时间。
驳船;遗传算法;适应值;惩罚函数;配载
1 引言
海洋结构物下水上驳船过程中压载水的调载作业一般都是操作人员利用以往的经验完成,但是,这种方式对操作人员的依赖性很大,作业过程效率不高,精确程度不够。
近年来大型海洋结构物不断增加,为了更好地控制产品上驳过程,一些基于驳船的智能配载方式便相应诞生。目前在国外,如挪威、美国、墨西哥等国家在驳船配载方面主要是通过不断地调节驳船的压载水来实现海洋结构物的下水安装作业[1-3]。但是,这些方法都没有进行方案优化,本文便是在此工程背景下,利用改进的遗传算法优化配载结果,使结构物上驳作业安全稳定、快捷高效。
2 遗传算法及其改进
遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。本文通过对遗传算法进行改进,采用种群全部交叉、1+n连续位扰动机制、劣种淘汰、分布式动态惩罚函数等多项比较灵活的处理种群基因的方式,使每一代种群既有良好的适应值又兼多样性。同时为了增加子种群之间的交流,在一定代数的子种群计算后,把子种群融合为一个种群进行大范围交流,限制子种群的非理想局部收敛。
本文中以一个大种群为例(多子群类似)把过程分为以下几个方面:
1) 计算染色体串长[4]
如果要求计算的精度达到小数点后K位,同时为了让参与遗传运算的每个变量为非负数,则二进制串长度及其解码方法可分别用式(1)和式(2)计算:

其中,LLi、ULi分别为自变量的下限和上限;decimal(substringi)代表变量 xi的十进位值。
2) 确定初始种群[5]
(1)每个变量在区间内进行离散,自变量的上下限要包括进来,即分别为首尾两个点。
(2)依次在每个变量内取一个划分的离散点xi,组成目标函数的可行解点列X = (x1,x2,…,xn),计算每个可行解的染色体适应值(不是目标函数值)。
(3)按照适应值的高低进行排序,从前到后取Popsize个染色体形成初始种群。
这种初始种群使自变量在可行解范围内均匀分布且适应值相对较高,利于后续的进化计算。而随机形成的初始种群很难在可行解范围内均匀离散分布,不利于全局收敛。
3)选择运算
本文选择操作的基本思想[5]是:
(1)计算群体中各个个体在下一代群体中的数目indivnumi

(2) 用整数 Int(indivnumi)确定各个对应个体在下一代群体中的生存数目。
(3)按照(2)中的方法一直取到第popsize-1个个体在下一代种群中的数目,剩余的种群基因数即为当代适应值最大的个体在下一代种群中的数目。
另外,本文的选择算子采用了“劣种变异”原则。其指导思想是:对每一代适应值比较靠后的个体(20%)用上一代保留的优秀个体进行变异若干次,取与劣种数量相同的适应值较大的变异个体作为劣种的替换。这种劣种淘汰方法提高了整个种群的竞争力。
4)适应度评价
种群适应值的计算是整个遗传算法的关键,关系着算法能否快速有效的收敛到全局极值。适应值的评价重在约束处理,对于约束的处理方法,常用的有算子修正法、可行解搜索法以及惩罚函数法[6],本文以分布式动态参数惩罚函数法对约束进行处理,具体适应度函数评价如(4)所示:
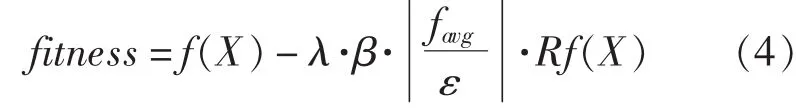
式中,f(X)为个体函数值;λ为固定罚因子,本文经过函数试验取为0.2;β为分段罚因子,即根据个体满足等式约束的程度而定;为自适应惩罚比例因子,其中,favg为当代所有个体目标函数值的平均值,ε为能够允许的超出约束的值,即约束允许误差;Rf(X)为实际满足约束的程度,在文中指超出约束的实际值,即

需要说明的是,在式(4)中分段罚因子β的确定尤为关键,本为是通过多个有代表性的函数试验进行确定的。为了说明β的分段划分情况仅以等式约束为例:针对不同的问题首先要确定一个等式约束允许的误差范围ε,根据种群不满足等式约束的值确定分段罚因子β。如果值越大,则β越大,反之则β越小。但β的分段值也不宜划分过细,过细容易把较好的个体淘汰掉,要针对具体问题具体分析,经过本文的函数试验其范围为0.8~1.5。
5)交叉操作
为了交叉后种群的多样性,本文令每一代种群全部参与交叉运算,其中每两个选中要交叉的父个体需要在不同交叉点进行很多次交叉运算,最后把交叉得到的所有新个体和父个体合在一起选择适应值最高的两个个体取代父个体进入后续的计算。该方法既增加了新个体的种类,也使得新个体适应值是不断增大的,具有良好的效果。
6)变异操作
参与变异运算的个体经过变异算子作用后,产生的新个体直接取代了原有个体,然而,新个体适应值是否有所提高,基本的变异算子是无法确定的。为了取得良好的变异效果,使得变异操作以后的新个体能够有一个较高的适应值,本文采用1+n连续位扰动机制进行变异,即让每个参与变异的父代在每个自变量所在的二进制代码中随机选取几个连续变异点。每个自变量需变异的位数视具体情况而定,文中是选择每个自变量二进制长度的10%的整数(至少为1位)。其中,每个个体进行mutanum(mutanum≥1)次变异,最后把变异产生的大量个体与父代一起进行比较,选择适应值最大的个体作为下一代的初始种群。
3 驳船配载优化
3.1 驳船配载原理及模型
对于不同的码头潮水涨退情况,驳船配载操作需要重点考虑的问题不一样。有些码头潮水涨退维持的时间比较短,驳船配载作业必须在较短的时间内完成,因而对驳船配载方案进行优化非常重要。本文以各待调节水舱调节前后的压载水的变化量为设计对象;以驳船的中纵剖面与基平面的交线为x轴,方向沿船首为正;驳船中横剖面与基平面的交线为y轴,方向沿右舷为正。设驳船压载舱共有N列,每一列有S个舱,从1到N列舱沿船尾到船首分布,第i列各舱从右至左舷的编号分别为:1,2,…,S。 值得注意的是,驳船横向一列舱一般是由一个泵控制,一列舱的排注水情况是相同的,虽然一列中各舱有单独的阀门控制,但是控制一列舱的泵的功率是不变的,从而决定配载操作时间的是一列舱的总流量,而不是一列中某个舱的流量,因此,在本文中以横向每一列为基本单位选择调节水舱。一般来说,选择其中的2列舱参与配载就可以满足工程要求,所以本文每次方案配载时选择其中的2列舱作为调节水舱。
配载操作中各调节水舱的水位确定主要与驳船的要求吃水(假设要保持滑道平齐)、上驳分段的实时重量和重心位置、各调节水舱的舱容要素、调节前各水舱的原有水位以及涨落潮实时水位等有关[7-8],其计算的理论基础是“双零原则”。 以驳船为研究对象,如图1所示,即驳船所受到的合力与合力矩为零。对于最后选定的最佳配载方案,需要校核最大剪力弯矩,如果该方案的最大剪力弯矩都满足要求,则最终确定该方案为本轮配载方案,否则,对次优方案验证,直至找到合适的方案。

图 1 中符号意义如下:Fb和(xb,yb)分别为驳船浮力及浮心坐标;GP和(LP,yP)分别为上驳分段压力及其作用点;GS和(LS,yS)分别为驳船本身的重力及其作用点;GW和(LW,yW)分别为驳船调载水重力及其作用点;G0W和(L0W,y0W)分别为驳船调载前压载水重力及其作用点。
在合力的作用下,驳船最终处于平衡状态,其衡方程可以式(6)表达为:
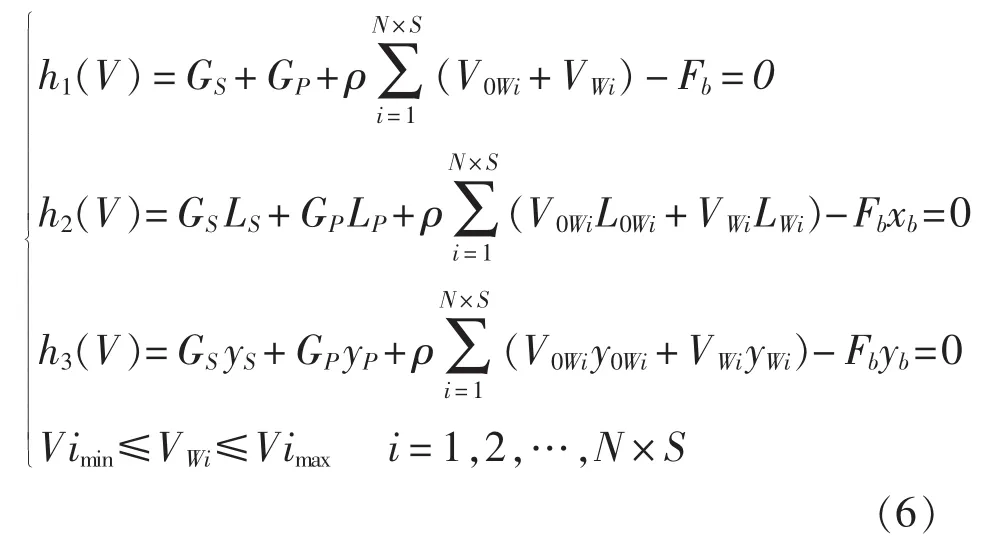
其中,ρ为水密度;V0Wi、VWi分别为第i个舱调载前水的体积和调载变化的水体积;h1(V)、h2(V)、h3(V)分别为力平衡方程、纵向力矩以及横向力矩平衡方程;Vimin、Vimax分别为第i个舱调节水体积的下限和上限,其余参数与图1中意义相同。
方案优化首先要选定两列调节水舱。为了方便遗传算法对数值的处理,首先必须对选定的两列舱进行排注水判断,即两列2S个舱最多只有两个符号。由于驳船横向一列舱的形状大致相同,所以其纵向型心基本相同,从而把一列舱作为一个整体考虑用于判断进出水符号是完全可以的。其具体判断方法可由式(7)~式(9)表达:
设被选择配载的两列舱其调载量分别为V1、V2,纵向力臂分别为 ML1、ML2,驳船达到预定浮态需要调节的水量和纵向力矩分别为ΔG和ΔMx,根据静力学的“双零原则”,则有:

本文中,纵向力臂为一列舱经过叠加得到的合力臂,其计算公式为式(8)。
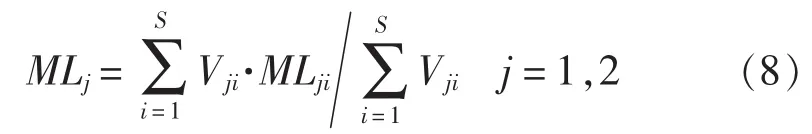
其中,MLji为某一列各舱的纵向力臂。
综上可知,利用简化处理方法可以得到两列舱的整体调水量由式(9)表示为:

如果两列舱整体调水量V1、V2都在允许调节范围内,则该方案继续进行,否则认为该方案不可行,直接进行下一个方案的计算。确定了进水或排水符号后,需要把两列舱中的2S个舱全部单独看做一个变量,其对应的配载优化模型可以写成(10)~式(12)所示的形式。

其中,ai和bi分别为调节水量的下限和上限;V0i和Vi分别为调载前的水量以及调载水量;LxS、Lxi、Lx0i、Lxp分别为驳船、调节水、原有压载水、上驳 分段 各重 心的 纵坐 标;LyS、Lyi、Ly0i、Lyp分 别 为驳船、调节水、原有压载水、上驳分段各重心的横坐标,其余符号意义与图1中相同。
鉴于基本遗传算法计算结果随机性比较大,即结果不稳定,本文以上文中提及的改进遗传算法为配载优化方法。其优化目标可描述为式(10)所示:设A代表所选择的两列舱 (如第1和第3列)优化的结果,即此时该两列的所有可行方案中调水量最大列比较的结果是A方案中调水最大列的调水最少,也就是操作时间最短,B代表所有A方案中(共个计算方案)调水量最大列结果最小的那个方案,则B即为目标函数所求解的最终方案。
3.2 驳船配载实例
上驳初始数据的选定直接影响大型结构物的滑移装船是否能够顺利完成,是产生预配方案的关键,同样也是指导实时配载的依据[9]。本文中以2列舱为研究对象,即上式中M=2。下面以某实际驳船数据为例,任意给定一个状态进行配载分析。其中,驳船有8列舱,每列4舱,左右对称。表1和2为产品和驳船的一些参数。

表1 上驳产品参数

表2 驳船参数
为方便叙述,规定文中符号如下:ΔG和ΔG’分别为需要调节的压载水量和实际调节水量;ΔMx和ΔMx’分别为需要调节的水量和实际调水量产生的纵向力矩;ΔMy和ΔMy’分别为需要调节的水量和实际调水量产生的横向力矩;[N]为配载过程允许出现的最大的剪力,本实例中[N]=1.87 × 103(tf);[M]为配载过程允许出现的最大弯矩,本实例中[M]=6.18×104(t·m);ε 为本次配载允许的超出3个等式方程约束的值,本实例中ε=10。 其约束如式(13):

本次配载为整个驳船配载方案中的一步调载情况,即由目前的驳船状态预配一段时间后(下一步配载)驳船对应的状态,本次方案如表3所示。对整个上驳过程的每一步调载按照本改进遗传算法和基本配载法[10]进行计算即可得到整个驳船配载的所有方案情况。
表3中的“基本”和“改进”分别为基本配载和运用改进遗传算法的配载方案结果,其中,基本配载方法为孙承猛[10]发表的博士论文中提出的“配对法”,其方法中利用了驳船的特殊结构,在压载舱横向和纵向配载的处理上对调节水舱的型心分别采用了类似文中式(7)~式(9)的简化处理。由于基本配载法为解平衡方程组法,所以结果无误差,而改进遗传算法的优化方法有一定的误差,其具体分析结果如表5所示。其中,实际误差为实际自变量满足合力与合力矩3个平衡方程的约束程度,其表达式为:
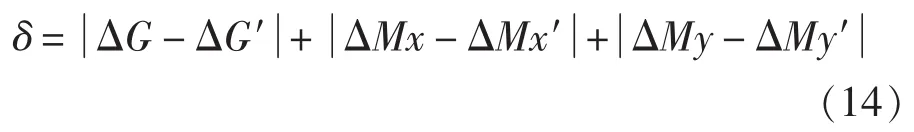
从表3和表4中的数据分析可以看出,相同方案时,基本配载法的单列最大调节水量更大,上驳作业时间更长。而改进遗传算法调节的最终结果显示,本次驳船配载的所有可行方案中的4个最优秀的方案都能满足工程上的要求,且都比相应的基本配载方案单列最大调节水量更少,即上驳作业时间更短,这4个优化方案的单列调节水量最大排列顺序为:354.75 t< 373.16 t<401.07 t<412.4 t,可见方案一中单列最大调载量最小,故方案一配载作业时间最少。同时方案一的最大剪力 Nmax= 1.14 × 103(tf) < [N] = 1.87 × 103(tf),对应产生的弯矩 Mmax=2.76×104(t·m)<[M]=6.18×104(t·m),实际误差 δ=6.47< 允许误差 ε =10,均满足给定要求,此即为本次配载最终方案。可见,应用本改进遗传算法对驳船配载模型的方案优化能够达到理想的效果。

表3 配载方案

表4 方案分析
4 结论
驳船配载问题与浮船坞的浮态调节类似,其实质可归结为求解一个约束优化问题[11],工程处理上一般会简化处理,不需要用很多列来调节,一般2列压载舱完全可以满足驳船配载的要求。本文从配载方案优化的角度出发,以2列压载舱的调水量变化为设计变量(N为舱列数,则有C种配载方案),应用基于分布式动态惩罚函数的改进遗传算法对配载作业时间进行了优化,使得配载作业在时间限制比较大 (较短时间内完成结构物上驳作业)的情况下可以很好地完成任务。此算法优化过程中应用了小生境遗传算法中的多个子群体并行运算模式,对函数多峰值情况处理有很好的效果。经过计算验证,该算法稳定,计算效率较高,对驳船配载实际工程的应用有一定的指导意义。本论文设计中有以下创新点:
1)首次在驳船配载模型中应用了遗传算法。
2)遗传算法的改进中,提出了种群全部交叉、1+n连续位扰动变异机制以及分布式动态惩罚函数法,使得遗传算法每一代能够得到最优秀的个体,利于种群稳定、快速地进化。
[1]COLE L G.The treatment of ship bi1ge, ballast and dock rain-water run-off by an electrox process[J].Ocean Engineering,1996,19 (8):72-74.
[2]HUA H,LEE P,WANG W.Analytical solution on the surge motion of tension-leg twin platform structural systems [J].Ocean Engineering, 2000,27:393-415.
[3]ARUP O.Solution for the shallows[J].Offshore Engineering,1998(1):42-43.
[4]雷英杰,张善文,等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.
[5]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.
[6]敖友云.基于遗传算法的连续函数优化技术研究[D].上海:上海师范大学,2006.
[7]杨星,季永青.集装箱船配载优化方法研究[J].武汉理工大学学报(交通科学与工程版),2002,26(2):223-226.
[8]王鸿鹏.一种优化编制船舶装载计划的新方法[J].集美大学学报(自然科学版),2002,7(1):38-44.
[9]杨晓宁.下水驳船自动配载研究[D].大连:大连理工大学,2008.
[10]孙承猛.下水驳船实时配载关键技术研究[D].大连:大连理工大学,2008.
[11]孙承猛,刘寅东.浮船坞实时配载模型及算法[J].大连:大连理工大学学报,2006,46(6):857-861.
Application of Improved Genetic Algorithm in Barge Stowage Planning Analysis
Xia Hua-bo Ji Zhuo-shang Zhang Ming-xia
School of Naval Architecture and Ocean Engineering,Dalian University of Technology,Dalian 116024,China
The barge is a common transportation widely adopted for launching large marine structures in the ship industry.Barge's stowage planning is conducted mainly depending on the adjustment of floating conditions in accordance with the hydrostatic balance principium and basic knowledge of ships.In order to complete stowage process in a short time,this paper applies an improved Genetic Algorithm (GA)to optimize ballast water's distribution, which propose improved approaches such as all-cross and distributed dynamic penalty function.The results show that stowage planning using improved GA is better than the basic planning in terms of time and efficiency.Improved GA to optimize barge's stowage can meet the engineering requirements and is time-saving for loading onboard the barge.
barge; GA; adaptive value; penalty function; stowage planning
U674.18
A
1673-3185(2010)06-51-05
10.3969/j.issn.1673-3185.2010.06.010
2009-12-18
夏华波(1984-),男,硕士研究生。研究方向:船舶结构物设计制造。E-mail:xiahuabo0303@126.com
纪卓尚(1938- ),男,教授,博士生导师。 研究方向:船舶结构物设计制造。E-mail:jizshang@ dlut.edu.cn
张明霞(1969 - ) ,女,副教授。 研究方向:船舶结构物设计制造。 E-mail:mxzhang@ dlut.edu.cn
