非均匀流场中螺旋桨线谱噪声指向性分析

谢剑波 周其斗

海军工程大学船舶与海洋工程系，湖北武汉 430033

非均匀流场中螺旋桨线谱噪声指向性分析

谢剑波 周其斗

海军工程大学船舶与海洋工程系，湖北武汉 430033

为了对非均匀流场中螺旋桨线谱噪声的指向性特征进行分析，在Ffowcs William－Hawkings方程的基础上，建立了非均匀流场中螺旋桨线谱噪声的频域预报理论，该理论可对声源在真实桨叶表面进行积分。讨论了螺旋桨叶数、来流谐波阶数以及叶片表面力对线谱噪声指向性的影响。结果表明，特征耦合系数是线谱噪声指向性分布形态的决定因素，并且当特征耦合系数等于零时，辐射噪声主要由轴向力和主要谐波所贡献；当特征耦合系数不为零时，轴向力和主要谐波的贡献只集中于桨轴方向，而桨盘面处的噪声贡献则来源于周向力和与叶片数目相等的谐波。

线谱噪声；螺旋桨；非均匀流场；噪声指向性；来流谐波

1 引言

螺旋桨噪声是船舶噪声源中一个很重要的分量。对于无空泡螺旋桨，由于其通常工作在船体形成的非均匀尾流场中，桨盘面处来流在空间上呈非均匀性［1-2］，因此，螺旋桨辐射的主要噪声是指桨盘面处非均匀速度场与旋转叶片相互作用所产生的线谱噪声以及由边界层湍流与旋转叶片相互作用所产生的宽带谱噪声，其中线谱噪声通常具有较高的幅值。非均匀流场中螺旋桨线谱噪声的幅值和指向性特征与螺旋桨参数以及来流情况均有关系，不少文献对噪声的幅值进行了研究［3－6］，然而对指向性的影响因素和变化规律进行研究的文献却很少。

通过将非均匀流场分解为来流谐波的组合，利用Ffowcs William－Hawkings方程，并结合带有平均流效果的格林函数的方法，得到了线谱噪声的频域预报理论，该理论可对声源在真实桨叶表面进行积分。应用该频域预报理论，数值预报了非均匀流场中的螺旋桨线谱噪声，并与试验结果进行了对比。对指向性的分析中，重点讨论了不同流场条件下线谱噪声指向性与螺旋桨叶数之间的变化规律，通过引入耦合系数和特征耦合系数，得到了指向性呈现偶极分布的判别条件。针对整体辐射噪声是所有来流谐波与叶片表面力综合作用的结果，探讨了来流谐波和非定常表面力对整体辐射噪声的贡献，并且讨论了当指向性平面旋转时的指向性变化规律。

螺旋桨噪声的理论设计和工程应用中，需要得到全方位的噪声特性，因此螺旋桨线谱噪声指向性研究对于开展低噪声螺旋桨设计以及衡量舰船噪声性能和进行水下目标识别都具有十分重要的意义。

2 线谱噪声理论

2.1 桨盘面处速度场

螺旋桨盘面处的来流具有不均匀性，根据实验及CFD理论模拟表明，在螺旋桨盘面上，还存在3个方向上的速度扰动，其中以轴向上的速度扰动为主，而径向和周向分量较之要小两个数量级，并考虑到轴向上的速度扰动是产生线谱噪声的主要原因，因此在噪声计算中通常只考虑轴向速度分量［7-8］。

在随螺旋桨平移的坐标系中，轴向来流速度u（r，θ）可表示为：

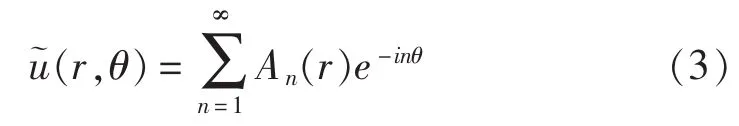
其中，An（r）为半径r处的第n阶来流谐波幅值。

2.2 翼面压力表示

将螺旋桨各截面当作二元机翼进行处理，则可根据Sears理论，得到翼表面的压力差。考虑到吸力面和压力面的压力幅值相等，相位相差π。因此，在桨叶固连坐标系中，桨截面上的压力分布可以表示为［9］：

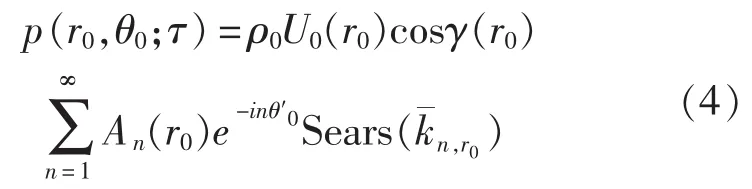
其中，γ（r0）表示半径 r0处的几何螺距角；U0（r0）表示半径r0处的平均来流合速度；n，r0表示第n阶来流谐波在半径r0处对应的无量纲波数；Sears（n，r0）为 Sears传递函数和弦向分布之积，定义为：

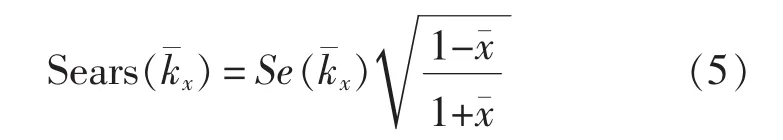
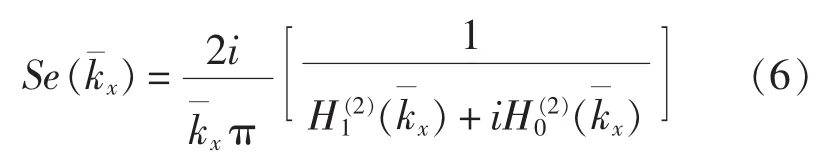
其中，H0和H1分别代表第0阶和第1阶Hankel函数。

2.3 线谱噪声预报

考虑低马赫数情况，在利用Ffowcs William－Hawkings方程时，可以忽略非线性四极子源和叶片厚度引起的体积排挤项，从而螺旋桨辐射声压的频域形式可以表示为：

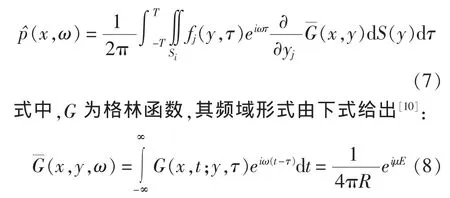
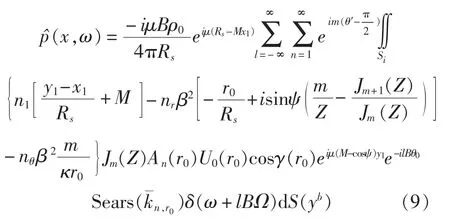
其中，l为辐射阶次；n 为来流谐波数，Z＝κr0sinψ，sinψ ＝r／Rs，m ＝IB-n 定义为桨叶与来流谐波之间的耦合系数。 Jm（Z）为第 m 阶贝塞尔函数，S（yb）为桨叶表面。从式中可以看出，该频域表达式可对声源项在真实桨叶表面进行积分。n1，nr和nθ分别表示叶片表面在轴向、径向和周向上的单位向量，因单位向量与叶表面压力的乘积为叶片非定常作用力，因此，当单独考虑 n1，nr和 nθ时，就可以非常方便的分析桨叶上非定常作用力对整体辐射线谱噪声的影响。

3 非均匀流场

Subramanian 和 Mueller［11］在消声风洞中对非均匀流场中的螺旋桨线谱噪声进行了测量，试验段平均风速为V0＝12.7 m／s，螺旋桨盘面处的非均匀来流由周向间隔的三隔板和四隔板产生，轴向速度Vx通过布置在不同半径上的热线风速仪进行测量。在θ′＝0°平面预先布置一组麦克风，用以测量噪声指向性，并通过旋转来流产生装置来测量不同指向性平面上的线谱噪声，来流装置和指向性平面如图1所示。

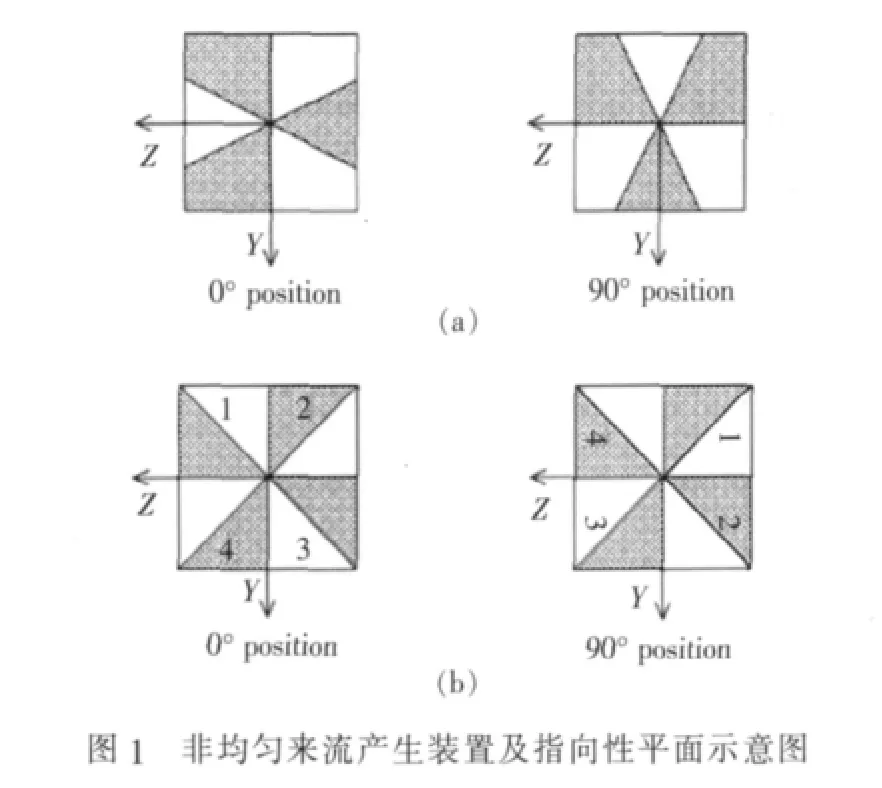
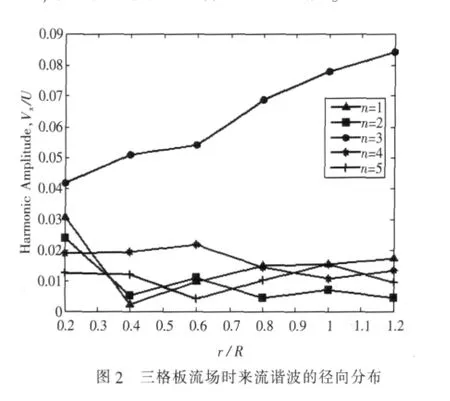
根据文献［11］测量的桨盘面处的轴向速度分布，可由式（1）～式（3）得到各阶来流谐波在径向上的分布。三格板和四格板形成的非均匀流场中，主要谐波分量沿径向的分布如图2和图3所示。

从来流谐波的径向分布图上可以看出，各阶来流谐波幅值取决于来流产生装置中格板的数量及其分布。三格板形成的非均匀流场中，第3阶谐波分量占主要成分；而四格板形成的非均匀流场中，第4阶谐波分量则占了主要成分。

4 线谱噪声指向性分析

文献［11］的试验中，所用桨为David Taylor研究中心设计的航空桨，编号为P3714，桨直径为0.250 4 m，毂径比 0.2，旋转速度为 3 000 r/min。辐射噪声采用麦克风进行测量，测量点位于15倍桨半径处，并通过改变麦克风位置测量噪声的指向性，在整个指向性平面上，共测量了9个点的辐射声压。

将螺旋桨桨叶离散成有限个三角形单元，并确保单元尺寸小于最大频率声波对应波长的1／8或 1／10，从而螺旋桨表面积分 dS（yb）就可转化为所有三角形单元积分的叠加。并将由式（1）～式（3）得到的各阶谐波分布代入式（9）中，可得到各阶线谱噪声的声压，进而根据空气中参考声压pref＝2×10－5Pa，可最终得到各阶叶频处的声压级。应用式（9）对三格板流场和四格板流场中的螺旋桨线谱噪声进行了数值计算，θ′＝0°平面上，预报值与试验结果的比较分别如图4和图5所示。

从图4和图5中可以看出，噪声预报值与试验测量值均符合较好，从而证明了文中所建立的线谱噪声频域预报理论的正确性。下面将在线谱噪声预报公式（9）的基础上，对线谱噪声的影响因素以及指向性变化情况进行详细的讨论。

4.1 线谱噪声指向性

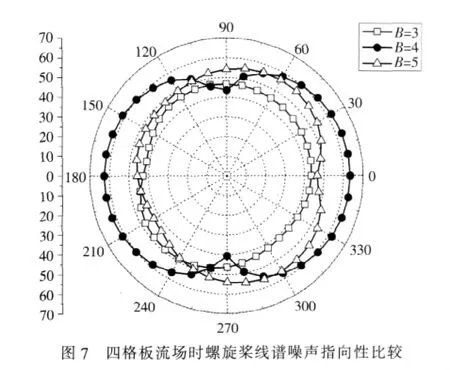
在三格板和四格板形成的非均匀流场条件下，对螺旋桨线谱噪声进行了指向性计算，在指向性平面为θ′＝0°时，不同桨叶数螺旋桨的噪声指向性分别如图6和图7所示。

从图6中可以看出：叶片数B＝3时，噪声在0°和 180°处（即桨轴方向）为最大值，而在 90°处（桨盘面方向）存在一个最小值，并且指向性关于桨轴和桨盘面对称，构成一个对称的轴向偶极子源辐射形式；而当叶片数B＝4，5时，指向性关于桨轴和桨盘面均不对称。

从线谱噪声预报公式（9）及贝塞尔函数性质可知，当耦合系数m＝IB-n＝0时，来流谐波与叶片的耦合作用最强烈。定义非均匀流场中主要谐波与叶片的耦合系数为特征耦合系数mc，所以在考虑第一阶辐射噪声l＝1时，对应于三格板流场，其主要谐波阶数为n＝3，当螺旋桨叶片数目B＝3时，就有特征耦合系数mc＝0，从而在指向性上体现为对称的轴向偶极子辐射形式。同时从线谱噪声预报公式（9）中也可以看出，当mc＝0时，径向力和周向力的影响可以忽略，轴向力部分n1［（y1－x1）／RS＋M］则可以简化为 －cosψ（考虑远场近似，即有 x1＜＜y1），从而预报公式（9）就可简化为：

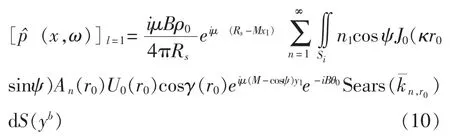
注意到零阶贝塞尔函数和余弦函数都是偶函数，因此上式就是关于ψ的偶函数，从而在指向性上就体现为关于螺旋桨轴对称。

而当叶片数目B＝4，5时，此时特征耦合系数mc＝IB-n≠0，叶片与谐波的耦合作用就相对减弱，同时径向力和周向力的影响也不能忽略，因此线谱噪声预报公式就不能简化为ψ的偶函数，从而在指向性上不构成对称的轴向偶极子辐射形式。

同理，对于四格板流场，当叶片数B＝4时，有特征耦合系数mc＝lB-n＝0，从而线谱噪声关于螺旋桨轴和桨盘面对称，在指向性上形成对称的偶极子辐射形式；而当叶片数B＝3或B＝5时，由于mc＝lB-n≠0，在指向性上就会形成不对称的分布，如图7所示。

4.2 指向性平面变化影响

上节为在θ′＝0°平面上的噪声指向性，实际应用中，有时需要得到全方位的噪声特性，因此，就必须对不同指向性平面上的线谱声进行数值预报，用以衡量全方位的辐射噪声特性。

图8所示为三格板流场时四叶桨在不同指向性平面上的辐射噪声特性。此时，特征耦合系数mc＝lB-n≠0。在所有指向性平面中，桨轴方向和桨盘面上的噪声值基本保持不变，变化最大的角度在30°和330°附近，这种变化特性主要取决于流场的非对称性。在除30°和330°这两个角度以外的其他点，下游噪声值比上游的值要大，呈现出从下游到上游的递减趋势，这与文献［11］的试验测量值结果相近。

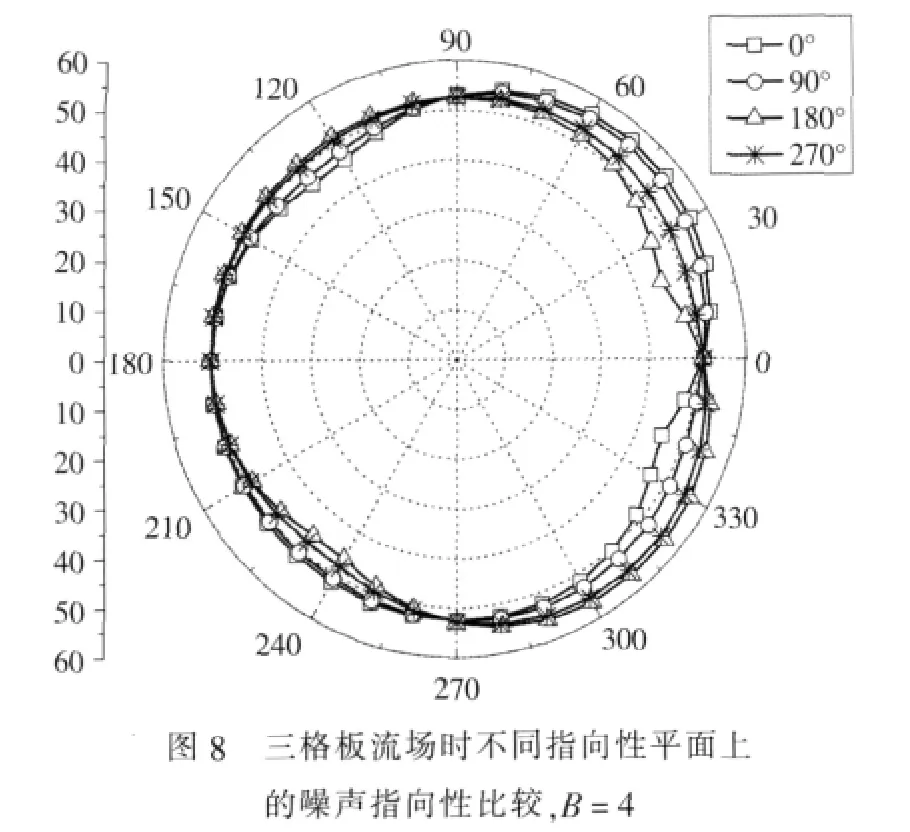
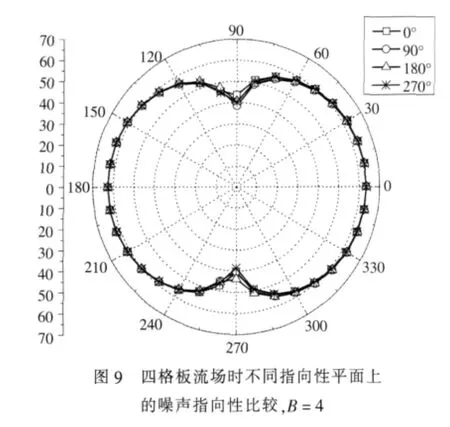
图9所示为四格板流场中四叶桨在不同指向性平面上的辐射噪声特性。此时，特征耦合系数mc＝lB－n＝0。可以看出，当指向性平面旋转时，相同角度处的噪声值基本保持不变。同时从线谱声预报公式（9）中也可以看出，反映指向性平面变化的主要影响项是有 e，从而当特征耦合系数mc＝lB－n＝0时，角度值θ′的变化对线谱声的影响就可以忽略不计。

4.3 谐波数的影响

由线谱噪声预报公式（9）中可以看出，辐射噪声是所有来流谐波与叶片相互耦合的综合作用结果，因此，讨论单个谐波对整体辐射噪声的贡献，有助于分析线谱声的产生机理，并进而为线谱声的控制提供相应的理论支持。图10所示为θ′＝0°指向性平面上，三格板流场时不同来流谐波对整体辐射噪声的贡献比较图。

从图中可以看出，整体辐射噪声主要由两个来流谐波所产生，即流场中的主要谐波n＝3以及与叶片数目相等的谐波n＝4，其中，n＝3阶谐波在桨盘面处起主导作用，而n＝4阶谐波则在桨轴方向起主导作用，并且其指向性呈现轴向偶极分布。

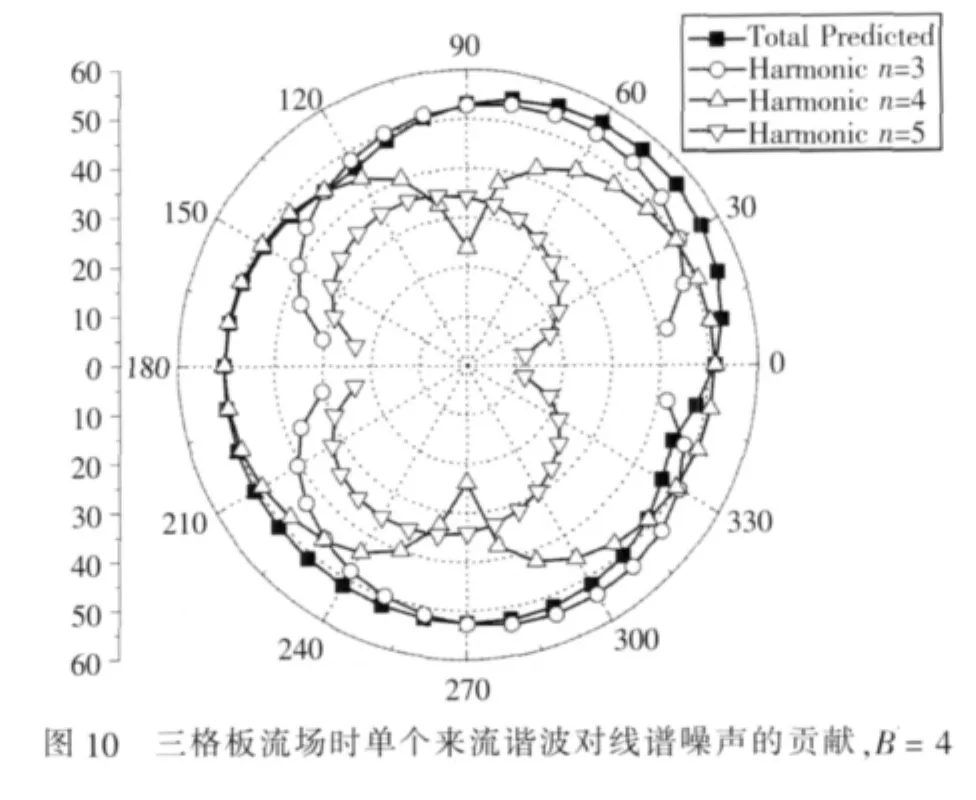
图11所示为四格板流场时不同来流谐波对整体辐射噪声的贡献比较图。此时，流场中主要谐波为n＝4阶谐波，其对应的特征耦合系数mc＝0。可以看出，在整个指向性平面上，整体辐射噪声主要由n＝4阶谐波，即流场中的主要谐波所产生，而其余阶谐波的贡献则相对很小。

4.4 力的影响

非均匀流场中来流谐波与叶片相互作用会在叶表面上产生非定常力，在轴向力、径向力和切向力的综合作用下，向外辐射线谱噪声。因此，分析不同力作用对整个辐射声场的贡献，对于了解线谱声的产生机理和影响因素具有十分重要的意义。

应用公式（9）进行线谱噪声计算并比较不同作用力的影响因素时，需要将叶片表面的单位向量n1，nr和nθ进行单独考虑，例如在计算轴向力对声场的贡献时，可只考虑n1部分，并忽略nr和nθ部分。图12所示为三格板流场中轴向、径向和周向力对整体辐射噪声的贡献比较图。可以看出，在整个指向性平面上，总辐射噪声主要取决于轴向力和切向力的贡献，其中，轴向力在桨轴方向上起主导作用，而切向力则在靠近桨盘面方向上起主导作用。

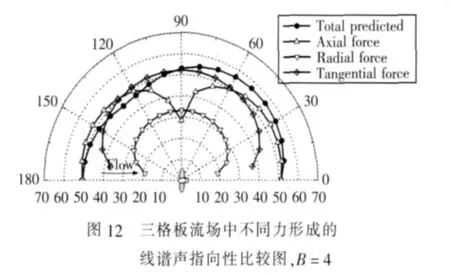
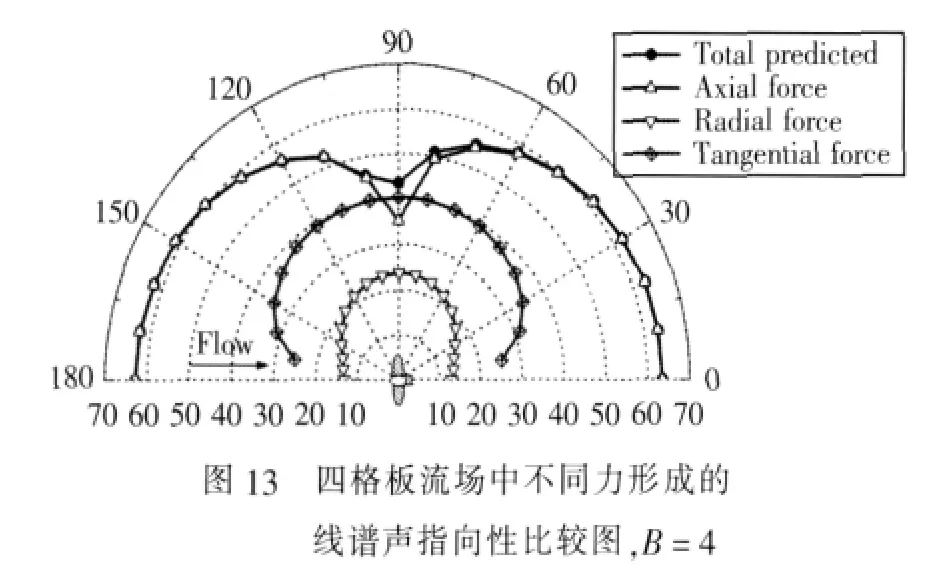
图13所示为四格板流场中轴向、径向和周向力对整体辐射噪声的贡献比较图。此时，特征耦合系数mc＝0，可以看出，在整个指向性平面上，总辐射噪声主要由轴向力决定，径向力的贡献最小，而周向力则只在桨盘面方向起一定作用。

5 结论

文中对非均匀流场中螺旋桨线谱噪声进行了研究，建立了线谱噪声的频域预报方法。对非均匀流场中的螺旋桨线谱噪声进行了数值计算，并与试验测量值进行了比较，两者符合较好，表明文中所建立的线谱噪声频域预报理论具有较高的计算精度。应用该理论，对线谱噪声指向性进行了相关的分析，得到了如下有意义的结果：

1）线谱噪声指向性形态取决于来流中主要谐波与叶片之间的特征耦合系数，当特征耦合系数等于零时，线谱噪声指向性呈现轴向的对称偶极分布；而当特征耦合系数不等于零时，指向性不呈对称性分布。

2）当特征耦合系数等于零时，指向性平面变化对同一角度处的噪声值影响不大；而当特征耦合系数不为零时，指向性平面变化对在轴向和桨盘面处的噪声值变化不大，而在其他角度处存在一定的变化，并且呈现出从下游到上游的递减趋势。

3）当特征耦合系数等于零时，辐射噪声主要取决于流场中的主要谐波；而当特征耦合系数不为零时，主要谐波以及与叶片数目相等的谐波对辐射噪声贡献最大，其中主要谐波在桨盘面处起主导作用，而与叶片数目相等的谐波则在桨轴方向起主导作用。

4）当特征耦合系数等于零时，总辐射噪声主要由轴向力决定，径向力的贡献最小，而周向力则只在桨盘面方向起一定作用；而当特征耦合系数不为零时，总辐射噪声则主要取决于轴向力和切向力的贡献，其中，轴向力在桨轴方向上起主导作用，而切向力则在靠近桨盘面方向上起主导作用。

［1］HUYER S A，SNARSKI S R.Analysis of a turbulent propeller inflow［J］.Journal of Fluids Engineering，2003，125：533－542.

［2］吴光林，严谨.船用螺旋桨理论研究的发展与方向［J］.中国舰船研究，2009，4（1）：8－12.

［3］张永坤，熊鹰，赵小龙.螺旋桨无空泡噪声预报［J］.噪声与振动控制，2008，44（1）：44－47.

［4］熊紫英，朱锡清，刘小龙，等.船尾伴流场－导管－螺旋桨互作用噪声预报研究［J］.声学学报，2009，34（2）：117－123.

［5］SEOL H，SUH J C，LEE S.Development of hybrid method for the prediction of underwater propeller noise［J］.Journal of Sound and Vibration，2005，288（1/2）：345－360.

［6］FEDALA D，KOUIDRI S，REY R.Numerical study of time domain analogy applied to noise prediction from rotating blades［J］.Journal of Sound and Vibration，2009，32（3/5）：662-679.

［7］HUYER S A，BEAL D.A turbulent inflow model based on velocity modulation ［J］.Journal of Sound and Vibration，2007，308（1/2）：28－43.

［8］MAUTNER T，GILLCRIST M.Obtaining the velocity field required for the calculation of propeller unsteady forces using “traditional” approximate methods and CFD［C］//30th Aerospace Sciences Meeeting ＆ Exhibit， Reno，NV，1992.

［9］MINNITI R J，BLAKE W K，MUELLER T J.Determination of inflow distortions by interpreting aeroacoustic response of a propeller fan［C］//4thAIAA/CEAS Aeroacoustic Conference， Toulouse， France； United States，1998：483-496.

［10］ZHOU Q， JOSEPH P F.Frequency－domain method for rotor self－noise prediction ［J］.AIAA Journal，2006，44（6）：1197－1206.

［11］SUBRAMANIAN S， MUELLER T J.An experimental study of propeller noise due to cyclic flow distortion［J］.Journal of Sound and Vibration，1995，183（5）：907－923.

Directivity Prediction on Tone Noise of Propeller Operating in Non-Uniform Flows

Xie Jian－bo Zhou Qi－dou
Department of Naval Architecture and Ocean Engineering，Naval University of Engineering，Wuhan 430033，China

In order to analyze the directivity performance of tone noise of propeller operating in a nonuniform flow， a numerical model， based on Ffowcs William－Hawkings equation， for predicting far－field propeller noise due to non－uniform flows is proposed which requires the aerodynamic sources to be integrated over the actual blade surface.The influence of blade number， inflow harmonic and unsteady blade forces on the directivity of radiated tone noise are discussed，which shows that the characteristics coupling factor between inflow harmonic and the rotating blades play important roles in the directivity feature.When the characteristic coupling factor equals to zero， the total radiated noise is mainly created by the axial force and the main inflow harmonic，while for the characteristic coupling factor not equals to zero，however， the noise contribution due to the axial force and the main inflow harmonic only dominate near the propeller axis，while the tangential force and the inflow harmonic that equals to the blade number dominate in the direction vertical to the propeller axis.

tone noise； propeller； non－uniform flow； noise directivity； inflow harmonic

U664.33

A

1673－3185（2010）06－06－06

10.3969/j.issn.1673-3185.2010.06.002

2010-02-09

谢剑波（1978－），男，博士研究生。研究方向：潜艇声学设计、螺旋桨噪声预报及控制。E-mail：xie＿jb＠126.com

周其斗（1962－），男，教授，博士生导师。研究方向：振动与噪声控制、水动力学。E-mail：qidou_zhou@126.com