复杂网络上聚集-部分消灭动力学的模拟

朱 标, 陈晓婷, 沈伟维

(温州大学物理与电子信息工程学院, 浙江 温州 325035)

0 前 言

聚集消灭演化动力学是近年来物理学研究领域的热点，聚集消灭现象广泛存在于自然界及人类社会当中，如聚合物的形成、生物种群之间的竞争、正负电子的湮灭和星云的分布等.近几十年来，聚集消灭动力学得到了深入的研究.1993年Krapivsky P L提出了两种类集团不可逆聚集-部分消灭动力学问题[1];1994年，Sokolov I M等人采用Monte-Carlo模拟研究了基于有边界条件规则网络上的由Krapivsky P L提出的不可逆聚集-部分消灭反应动力学过程[2]；Ben-Naim E 和Krapivsky P L于1995年研究了两种类集团的聚集-完全消灭模型[3]；2003年Ke J等人提出了含有两种类集团的系统存在聚集和单体消灭两种机制的反应模型[4].

在过去的研究中，研究者大多运用平均场假设下的Smoluchowski速率方程进行理论研究或者基于规则网络进行计算机模拟.无论是理论研究还是计算机模拟，反应物大小在空间的涨落必须忽略，且假设各种类聚集体集团在整个反应过程中是均匀分布的，即反应物集团的空间扩散系数为无限大，认为系统中每一对集团相互反应的概率是相等的.如果将动力学演化过程用网络描述，每一个集团可以抽象成节点，若集团之间有联系，则两节点之间有边存在，这样我们就可以把聚集消灭反应动力学过程抽象为在网络上的动力学演化.但是在已有的研究中，基于动力学反应过程的背景都被认为发生在规则网络或随机网络上，然而在真实世界中，很多事件之间的联系往往表现出小世界效应和无标度特性，即系统中的集团不能看成是完全等几率反应的，不仅近邻节点间可以发生反应.两个远程节点上的集团也可以发生反应，所以真实世界里的一些反应过程不能简单的被认为是在规则或者随机空间里进行的，而应该被看成是发生在复杂网络上的动力学过程[5，6]，况且已有很多研究结果表明,基于复杂网络的一些反应系统与正规空间的相同系统有着显著不同的动力学行为[9-15].本文采用Monte-Carlo模拟在复杂网络上的聚集部分消灭动力学行为.

1 基于复杂网络上的聚集部分消灭动力学模型

在网络中对于每一个节点，在任何时刻都含有3种可能的态：m、0和-n.节点处于m态表示该节点被m个A种类粒子同时占据，而节点处于0态表示没有粒子占据该节点(即空节点)，节点处于-n态表示该节点被n个B种类粒子同时占据.为了简化反应过程，我们假定初始时刻只有若干节点被粒子占据，且只能被一个粒子占据.该动力学演化机制在网络中的聚集消灭反应包含以下几个步骤：(1)随机选择一个有粒子存在的节点i；(2)从节点i的相邻节点随机选择一个节点j；(3)i节点上的粒子全部移到j节点上.如果节点j为空节点，则粒子占据j节点.如果j节点已有粒子，则将遵循1993年由Krapivsky P L 提出的聚集-部分消灭动力学机制[3]：

此时j节点的粒子数将是|m-n|，粒子种类由m和n的大小决定.在一些实际过程中，集团的质量影响集团扩散速率.一般而言，较大质量的集团扩散速率相对较小，质量较小的集团扩散速率则相对较大，所以本文引入扩散系数D表征扩散速率对集团质量的依赖关系.通常，扩散系数D与集团质量m的关系可写为D～m-q，q越大，则D越小，质量越大的集团越难发生迁移.

1.1 二维规则网络上的聚集部分消灭动力学

图1 二维正方规则网络 图2 二维环状规则网络

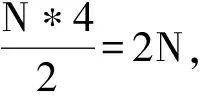
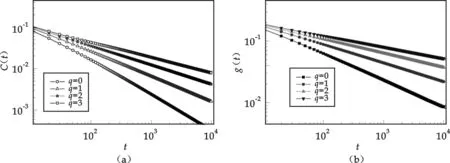
图3 二维环状规则网络集团浓度和粒子浓度随时间的变化曲线

q0123α0.859 280.606 680.462 730.376 71β0.445 540.304 980.232 030.188 15

1.2 小世界网络上的聚集部分消灭动力学

1998年，Watts D J和Strogtz S H引入了WS小世界网络模型[7]：该模型在低维的规则网络的基础上通过随机化重连边而构造，但是该构造算法容易破坏网络的连通性.在本文的研究中，我们需考虑系统中的所有粒子参与反应过程，因此本文讨论基于NW小世界网络的不可逆聚集-不完全消灭反应模型.NW小世界网络是由Newman M E J和Watts D J提出(称NW模型)[8]：该模型在低维规则网络的基础上通过随机化加边构造，不会破坏网络的连通性.

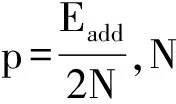
1.2.1 集团扩散速率与大小无关的聚集-部分消灭过程(q=0)

下面给出不同捷径化参量p下，网络的平均最短路径以及反应中期和中后期幂律指数α、β的值.反应中期所指时间段为计算机模拟的100～1 000步，而反应中后期所指的时间段为1 000～10 000步.

表2 q=0时不同捷径化参量p下幂指数α、β的值

续表2

pLα中期中后期β中期中后期0.0118.009 210.897 610.909 230.445 640.454 610.0313.057 190.921 370.933 130.449 570.466 570.0511.262 010.925 190.937 450.453 720.468 730.0710.206 930.927 730.947 640.458 610.469 610.19.212 180.935 750.949 220.462 860.473 820.36.738 050.943 470.955 380.472 690.477 690.55.840 440.954 990.955 860.476 830.477 930.75.321 230.955 460.955 450.476 730.477 7314.817 360.955 460.955 460.476 830.477 73

模拟结果表明，基于二维小世界网络的聚集部分消灭动力学过程剩余的集团浓度c(t)和粒子浓度g(t)随时间的演化关系同样都满足幂律关系.由表2可见，随着捷径化参量p的增大，幂指数α和β的值增大，且幂指数α和β的值均满足α=2β的关系，与二维环状规则网络的不可逆聚集-部分消灭动力学反应相一致.这表明，网络结构的改变仅影响了不可逆聚集-部分消灭反应系统的演化速率，并不会影响系统的标度性质.

图4 不同时间段集团浓度幂律指数α随捷径化参数p变化的曲线 图5 不同时间段粒子浓度幂指数β随捷径化参数p变化的曲线

表3 q=1时不同捷径化参量p下幂指数α、β的值

比较图4、图5中不同反应时期的幂指数的大小，我们发现：(1)p较大或较小时，两个反应时期的幂指数α(β)近似相同，表明反应系统经长时间反应后，系统中剩余的集团密度和粒子密度随时间的演化严格遵循按幂律函数形式；(2)p为其他值时，反应中后期的幂指数α(β)值略大于反应中期相应的α(β)值，即集团密度和粒子密度随时间的演化近似地按幂律形式演化.由此可见，随机加边带来的捷径在不同反应时期对不可逆聚集-部分消灭反应系统的演化有着不同的影响.当捷径化参量p较小时，即加的边很少时，虽然平均最短路径相对于p=0(规则网络)时减小很多，但是网络中所添加的捷径(共2Np条)相对较少，集团在反应过程中选择这些捷径作为通道的概率很小，即随机添加的少量边对聚集消灭过程的反应历程影响很小.随着捷径化参量p的增大，即加边数的增加，幂律指数增大到一定程度后开始趋于稳定，也就是说当边数加到一定程度后网络环境基本上已经接近平均场情况.本身二维环状规则网络的维度为2，随着p的增大，平均最短路径逐渐减小，网络的维度逐渐增大.文献[14]研究结果表明，一旦系统所处的空间维度大于临界维度(dc=2)，则反应物浓度的空间涨落可以忽略不计.另一方面，基于平均场的理论计算结果表明[1]，当t>>1时，幂律指数α=1,β=0.5.对于二维小世界网络的维度一定大于2，从表2我们已经看到，随着捷径化参量p的增大，幂律指数逐渐趋近于平均场的计算结果.

1.2.2 集团扩散速率与大小有关的聚集部分消灭过程(q=1)

图3给出了不同捷径化参量p下网络的平均最短路径以及反应中期和中后期幂律指数α、β的值.

在不可逆聚集-消灭反应过程中，集团的扩散速率与其所包含的粒子数m成反比，而且所有集团的质量m≥1，因此与上述q=0情况相比，q>0情况下系统的演化速率更加缓慢.

2 结束语

参考文献

[1] Krapivsky P. L.. Nonuniversality and breakdown of scaling in two-species aggregation with annihilation[J]. Physica A, 1993,198:135.

[2] Sokolov I. M., Blumen A.. Kinetics in coagulation-annihilation processes[J]. Phys. Rev. E, 1994, 50: 2 335-2 338.

[3] Ke J., Lin Z.. Kinetic behavior of aggregation process with complete annihilation[J]. Phys. Rev. E,2002,65:107.

[4] Ke J., Lin Z.. Solvable aggregation model with monmer annihilation[J]. Phys. Rev. E,2003,67:101.

[5] Albert R., Barabási A. L.. Statistical mechanics of complex networks[J]. Rev. Mod. Phys., 2002,74:47.

[6] Dorogovtsev S. N., Mendes J. F. F.. Evolution of networks[J]. Adv. Phys., 2002,51:1 079.

[7] Watts D. J., Strogatz S. H.. Collective dynamics of “small-world” networks[J]. Nature,1998,393:440.

[8] M. E. J. Newman， D. J. Watts. Renormalization group analysis of the small-world network model[J].Phys. Lett. A,1999，263:341-346.

[9] Gallos L. K., Argyrakis P.. Absence of kinetics effects in reaction-diffusion processes in scale-free networks[J]. Phys. Rev. Lett., 2004, 92:138-301.

[10] Gallos L. K., Argyrakis P.. Influence of a complex network substrate on reaction-diffusion processes[J]. J. Phys.: Condens. Matt., 2007, 19:065-123.

[11] Tang M , Liu Z , Zhou .Condensation in a zero range process on weighted scale-free networks[J]. Phys. Rev. E.,2006 ,74 :036-101.

[12] Hua D. Y.. Dynamics of symmetric conserved mass aggregation model on complex networks[J]. Chin. Phys. Lett.,2009,26:901.

[13] Ke J, Lin Z, Zheng Y,etal. Migration-driven aggregate growth on scale-free networks[J]. Phys. Rev. Lett., 2006,97:301.

[14] Kang K., Redner S.. Fluctuation effects in smoluchowski reaction kinetics[J], Phys. Rev. A, 1984, 30:2 833.

[15] Krapivsky P. L.. Exact solutions for aggregation-annihilation processes in one dimension[J]. Physica A, 1993, 198:150.