基于车辆跟驰模型的交通流动力学模型

杨文杰， 白云霄， 贾宏恩

(1.陕西科技大学理学院， 陕西 西安 710021; 2.西安交通大学理学院， 陕西 西安 710049)

0 引言

随着经济建设和社会的发展，交通问题越来越成为人们关注的热点，交通流理论的研究随之迅速开展.同时，由于其学科的交叉性，交通流理论也受到了力学、应用数学、交通工程和控制理论等领域许多专家和学者的重视.

目前，交通流理论的研究方法包括跟驰模型、动力学模型(也称为连续介质力学模型) 、分子动力论方法及元胞自动机方法等[1].动力学模型和跟驰模型是其中最具影响和代表性的两个大类，前者由于其宏观性质而在应用中得以较快地发展，后者则因其微观性而可以作为对前者的补充[2].而且，由于它们是从不同的角度来研究交通流的演化规律，故所建立的基础在一定意义下是一致的.基于这样的认识，本文首先从微观跟驰模型出发，考虑到前后两车的速度差和距离差对于交通流动态变化规律的影响，对已有的跟驰模型做了修改和完善，建立了新的微观跟驰模型；在此基础上，利用微观与宏观之间的联系，建立了宏观的交通流动力学模型，并对其进行了数值模拟.

1 跟驰模型的研究和改进

跟驰理论最早是由Pipes L.A[3]于1953年提出的，它主要采用刺激反应模式，研究在单一车道上车辆排队行驶时后车跟随前车的行驶状态，其具体表现形式为：

跟踪反应=敏感度×刺激因素

在车辆跟弛过程中，后车的运动情况受多种因素的影响和制约，比如前后两车的速度差、距离差、司机的个性特点、天气、路况等.然而，在实际建模过程中，由于研究者出发点、兴趣的不同，又导致了各种不同的跟驰模型的出现，其中比较有代表性的模型有Bando[4]等人于1995年提出的称为优化速度的(OVM)跟弛模型，其形式为

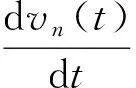
(1.1)

其中v(Δx)称为优化速度，取决于两车间距Δx;kI为敏感系数.模型(1.1)考虑了两车间距和本车速度的影响，但是模型没有考虑前后车速度差的作用.应用该模型可以模拟实际交通流的许多定性特征，如交通失稳、阻塞演化、走走停停等，但是与实际观察数据相比，OVM模型有过大的加速度或不切实际的减速度.

Helbing等人在OVM模型的基础上又提出了广义力学模型(GFM)[5]，其形式为：

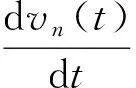
(1.2)

其中当x≥0 时，H(x)=1；当x<0时，H(x)=0.模型(1.2)克服了OVM模型中加速度过大的问题，但是模拟结果显示，与实际观察数据相比，所得结果的启动车辆推迟时间过长，且启动时小扰动传播速度过慢.

在此基础上，我国学者姜锐、吴清松等于2001年提出了称为完整速度差(FVD)的跟弛模型[6]，其形式为：

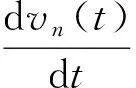
(1.3)

该模型更好地反映了实际交通的特征，可以克服OVM模型加速度过大的问题.

在文献[7]中基于跟随车的速度只与前后车的距离差有关而给出了如下的跟驰模型：

(1.4)

其中xn(t)为t时刻第n辆车的位置，xn-1(t)为t时刻第n-1辆车的位置，T为驾驶员对前方刺激做出反应的滞后时间，G(xn-1(t)-xn(t))为前后两车距离差的函数.

根据对车辆跟弛现象的观察，我们认为跟弛车的速度不但取决于前后两车的距离差，而且与前后两车的速度差有关，基于这一思想，我们提出了如下的跟驰模型：

(1.5)

其中λ>0为一无量纲常数.

模型(1.5)充分考虑了前后两车的距离差、速度差对跟随车加速度的影响，使得只考虑速度差时，在前后车速度相等的情况下，不管两车距离有多远，跟随车都不会加速的这种现象不会出现，同时也避免了只考虑距离差时，前车突然加速，而后车不会作出反应的现象.事实上，处于跟驰状态的两辆车，跟随车的速度总是在前导车速度附近波动，既不会长时间超过前导车速度以致撞车，也不会长时间低于前导车速度以致落后.当前面的车辆突然加速或减速时，跟随车会很快作出反应，在Δvn>0时，即车间距小于安全距离时跟随车仍可以加速，因而同时考虑距离差和速度差对加速度的影响是很有现实意义的.

下面我们将从(1.5)式出发，利用微观与宏观之间的关系，导出一种新的动力学模型.

2 模型的建立

在式(1.5)中，如果我们令

(2.1)

那么式(1.5)就等价于如下两个方程:

在此为了将其转化为连续性的方程，引入连续性的变量v(x,t),h(x,t),使其满足：

(2.3)

则方程(2.2a)可以写为：

此时求解在小T和小hn下的偏微分方程组,由泰勒展式展开，我们只保留线性项，有：

(2.4)

又因为式(2.2b)可写为：

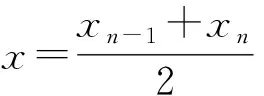
ht+vhx=hvx

(2.5)

作为近似.

此时，利用ρ=1/h,V(ρ)=G(h),式(2.4)、 (2.5)可以化为

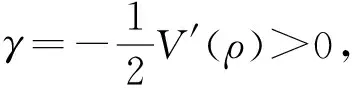
在模型中γ>0，这主要是由于前面的密度不断增加，司机将进行减速，反之则进行加速.同时密度梯度的存在，意味着某地的车流速度不再由当地的密度值决定，而是依赖于其前方某处的密度值，且可以抑制低密度区的车流向高密度区的移动；反之，则加速了高密度区车流向低密度区的扩散.速度梯度的存在说明前面车辆加速时，后面的车辆也将跟着加速，反之，则要减速，这种加速、减速的反应在跟驰状态中表现得尤为明显.也就是说，驾驶员会根据前面车流的密度与速度分布情况来调整自己的车速，使两车的车头间距趋于正常.

注1：在式(2.6b)中，若令λ=0，即得Payne模型；若令λ=0，k=0，V(ρ)=uf,即得Ross模型，其中uf为自由畅行速度(free flow speed).

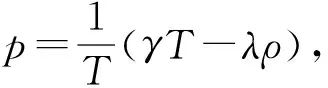
(2.7)

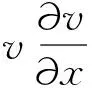
3 差分格式的构造与数值模拟

在式(2.6b)的两边同乘以ρ,则得

化简后可得：

从而可将原方程组(2.6)化为：

(3.1)

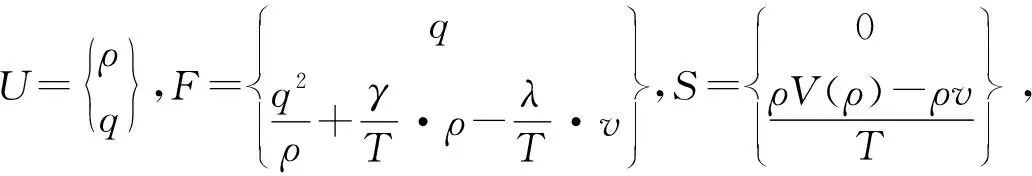
(3.2)

更进一步地，我们可以把方程(3.2)化为如下的拟线性形式：

鉴于高阶模型易产生不切实际的振荡和一些非线性的数值不稳定性，特别是对于较大的梯度[9-11],而一阶精度的格式在交通流的模拟中则显示出良好的性能，因此在这里我们选用一阶精度的Lax-Friedrichs 格式[12]：

进行数值模拟，其稳定性条件(CFL条件)为：Δt≤Δx/vf，其中n是时间步序号，j是空间步序号，T是滞后时间，Δt是时间步长，Δx是空间步长.

下面我们通过算例来研究模型的有效性.

算例1. 上游高密度下游低密度的演化情况.

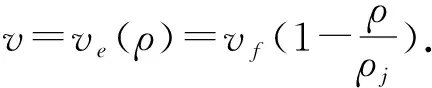
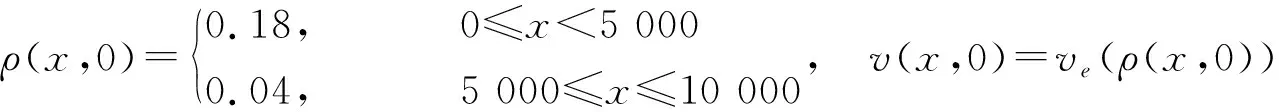
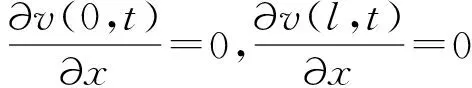
计算结果如图1、图2所示.

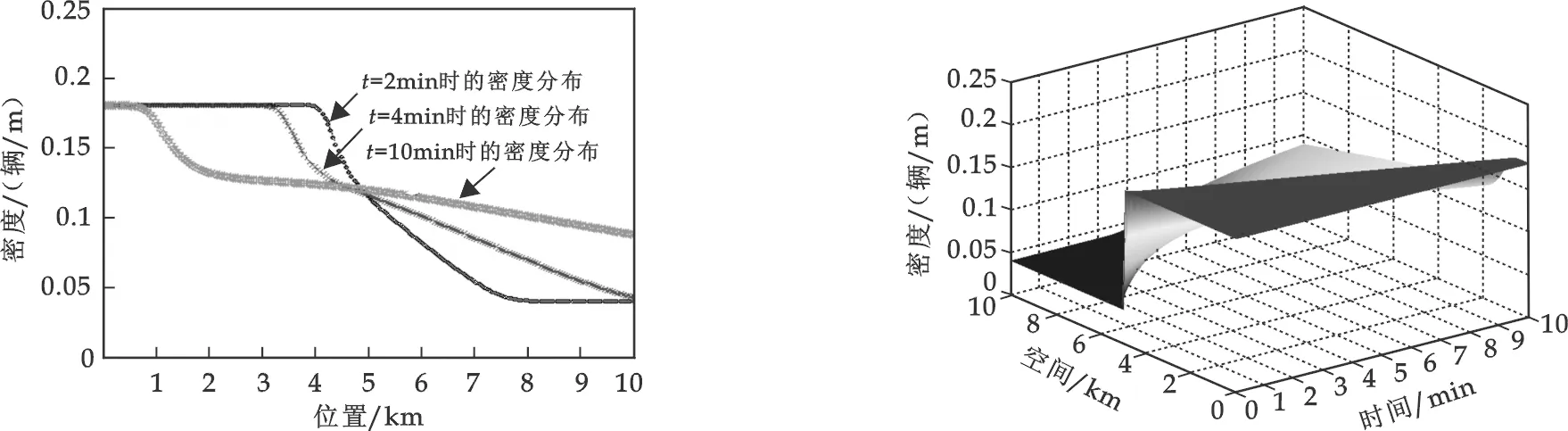
图1t为不同时刻的密度分布 图2 密度分布的时空演化图(0～10 min)

在计算中,取时间步长Δt=1 s，空间步长Δx=50 m，γ=0.3,k=0.2.

算例2. 考虑交通流局部密度增大后消散的过程.

设最大密度ρj=0.9，最大速度vf=20 m/s，路段长l=10 km，司机的反应时间T=2.5 s，ρa=0.6.

初始条件：

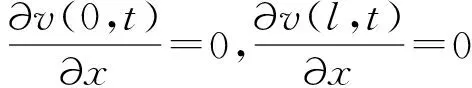
计算结果如图3、图4所示.

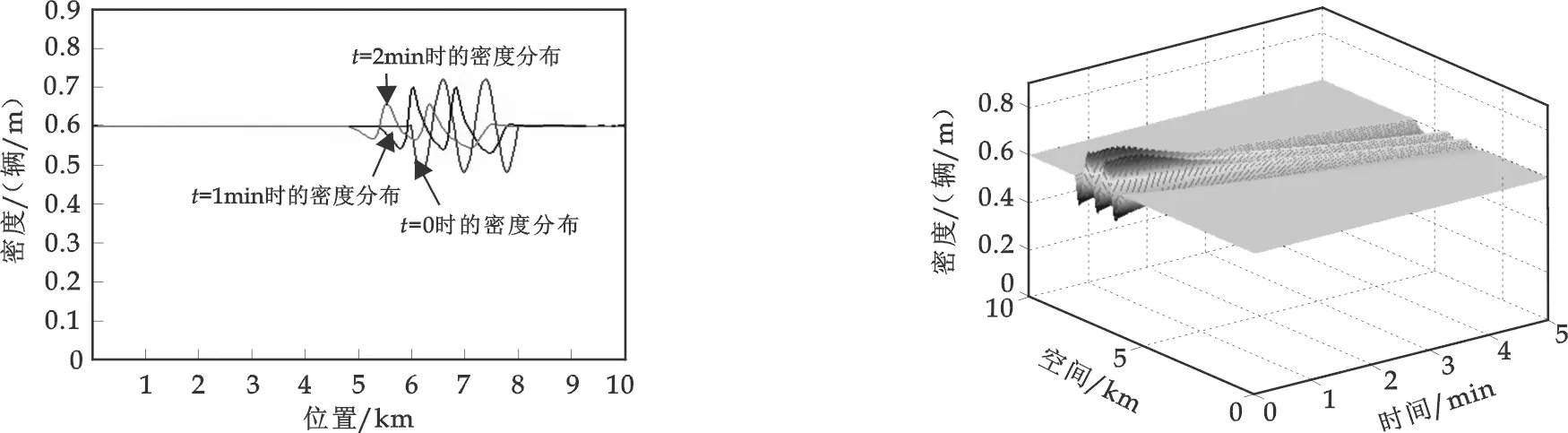
图3t为不同时刻的密度分布 图4 密度分布的时空演化图(0～5 min)

在计算中，取时间步长Δt=1 s，空间步长Δx=50 m，γ=0.3,k=0.2.

从模拟结果可以看出，在算例1中，上游高密度的车流随时间向下游低密度区疏散，产生了交通稀疏波，这与交通流的性质是一致的，同时也与文献[10]的模拟结果一致；在算例2中，在初始时刻路段中间发生扰动，当扰动不太大时，由于扰动而引起的密度增大随着时间的推移会逐步消散，而且从图中也可以看出，局部密度增加如图3那样传播，并在其后部形成一个激波.实际上，有的汽车速度比较快，因此司机是从后面进入这样一个局部密度增加的区域，在穿过激波时须迅速减速，但当其离开交通拥挤的地方时只能慢慢加速，这是与实际相一致的.而且，进一步的模拟显示当α>0.25时，扰动引起的密度增大，且会一直持续下去，直至堵塞.这充分说明稳定车流在一定范围内的小扰动将逐步消失，随着车流密度的增加，扰动发展成堵塞，形成局部集簇(local cluster),即所谓的时走时停现象.

4 结束语

本文在对交通流模型的研究进行简单回顾的基础上，以跟驰模型为出发点，主要采用微观转化为宏观并线性近似的研究方法得到了新的交通流动力学模型，同时在不同的边界条件下，对不同的算例进行了数值模拟，结果显示模型可以较好地捕捉到交通激波的形成、阻塞的形成与疏导以及车流的小扰失稳等交通现象，进一步的模拟显示，该模型还能较好地模拟幽灵塞车及相转变等交通现象，这些结果不但符合波的演化规律，而且与交通流的演化规律相一致 .

当然，由于数据采集的局限性，该模型的有效性仍需要更多数值模拟结果的检验，同时在模型的提出方面我们可以肯定的是前后车的距离差与速度差对跟驰车的加速度都有影响，且文献[11]中已提出，对跟随车驾驶员进行速度调节，反应最强的还是两车的速度差，但其所占的比重有多大，也就是参数λ的大小，仍有待于我们进一步去研究.

参考文献

[1] Helbing D,Treiber M.Traffic theory-jams,waves and clusters[J].Science,1998,282:2 001-2 003.

[2] Zhang Peng,Liu Ruxun.Analyses and remarks on traffic flow model along with its improvement[J].Journal of Kunming University of Science and Technology，2000,25(4):118-123.

[3] Pipe.L.A.A operational of traffic dynamics[J].J.Appl.Phys,1953,24:274-281.

[4] Bando M,Hasebe K,Nakayama A,etal.Dynamical model of traffic congestion and numerical simulation[J].Phys Rev E,1995,51:1 035-1 042.

[5] Helbing D,Tilch B.Generalized force model of traffic dynamics[J]. Phys Rev E,1998,58：133-138.

[6] 姜 锐,吴清松,朱祚金.一种新的交通流动力学模型[J].科学通报，2000，45(17)：1 895-1 899.

[7] Whitham G.B.Linear and Nonlinear Waves[M]. Wiley-Intescience, New York,1974.

[8] Phillips W F.A New Continuum Traffic Model Obtained from Kinetic Theory[R]. IEEE Trans.Autom.Control.AC-23，1978:1 032-1 036.

[9] W.H.Press, S.A.Teukolsky, W.T.Vetterling,etal. Numerical Recipe in C:The Art of Scienfic Computing[M]. Cambridge University Press, Cambriage,2nd edition,1992.

[10] 张 鹏,刘儒勋.交通流问题的有限元分析和模拟(Ⅰ)[J].计算物理,2001,18(4):329-333.

[11] 许伦辉,徐建闽.车辆跟驰问题的建模及其求解[J].华南理工大学学报,1998，26(9):38-43.

[12] R.J.LeVeque. Numerical Methods for Conservation Laws[M]. Birkhǎuser,Basel,1992.