基于耦合模态控制算法对空间结构主动控制的试验研究

杜园芳， 王社良， 张 博

(1.中国煤炭地质总局航测遥感局， 陕西 西安 710054； 2．西安建筑科技大学 土木工程学院， 陕西 西安 710055)

智能结构主动控制技术具有较大的灵活性、智能性、高效性和对环境的适应能力强等优点，在结构振动控制领域有着良好的应用前景和发展前途[1]。与传统的振动控制方法对比，传统的方法是通过结构元件的刚化，谐振系统的解谐与解耦，普通振动隔离，阻尼隔振，动力吸振等方法实现，主要依靠结构本身的阻尼消耗振动能量。而压电智能材料的应用及其相应通过解耦进行控制的模态空间控制技术的实现，使得智能材料在土木工程中得到应用，并能够满足人们对结构的性能更高的要求。

1 压电材料杆件的主动控制设计原理

压电材料具有正逆压电效应，因此既可以做传感器又可以做驱动器，但是一般压电材料的压电应变系数很小，即使施加很大的电压，输出位移也较小[2]。因此采用多组压电片在力学上串联、电学上并联的设计思想而构成的压电堆，使各压电片产生的位移可以叠加输出，增加了位移输出量，是主动杆件的核心部分[3]。压电堆的受压方向与主动杆件保持一致，当结构受到动荷载作用时必定会发生相应的振动[4]，此时主元杆件将发生一定的变形，压电堆产生的电荷量为：

(1)

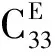
V=K×q(t)

(2)

其中，K为电荷放大系数。

当主元杆件受到驱动电压的作用时，通过控制电压的相位差，使其达到180度，杆件便会受到一定的干扰力[5]，具体计算公式为：

(3)

其中，μ为泊松比；Ap、Ep分别为压电堆的截面面积与弹性模量；n为压电堆个数；t为单片压电片厚度。

2 模态控制理论

模态控制法是无限自由度系统,通常可以用其低阶自由度系统在模态空间内少量的几个模态来近似描述[6,7]。具有反馈控制的结构的线性离散化动力学方程为：

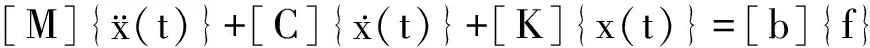
(4)

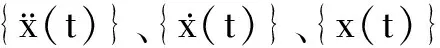
{x(t)}=[φ]{q}

(5)

式中，{q}是N维模态坐标矢量；[φ]为模态矩阵。将式(5)代入式(4)可得：

(6)

其中，ωi是开环无阻尼系统的第i阶固有频率，ξi是开环系统第i阶模态阻尼比。

各分量满足方程：

(7)

Fi为第i阶模态控制力。

若Fi表示为：

(8)

其中i=1,2,…,N;gis，his分别为模态控制位移增量和速度增量。

则在有控情况下的闭环系统方程为：

(9)

由式(9)可以看出，对于独立模态控制，各阶模态都是独立的，可以很方便的进行控制律的设计。实际控制力为：

(10)

将式(4)转化为状态方程：

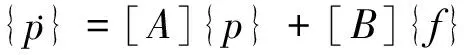
(11)

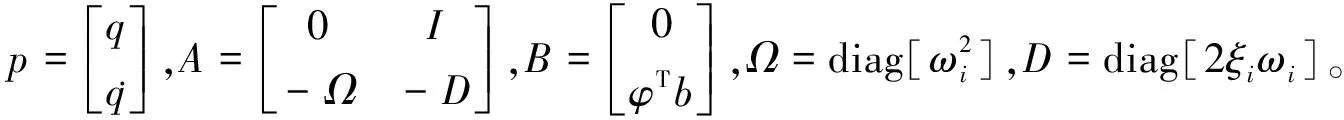
控制性能指标可以表示为：

(12)

相应的最优控制力为：

{f(t)}=-[R]-1[B]T[G]{p}

(13)

其中，Gi为如下形式的Ricaati方程的解：

(14)

从以上各式可以看出，在采用耦合模态控制时，第i阶模态控制力Fi的大小依赖于所有被控模态坐标的值，同时，一个作动器对所有的模态均有控制作用，因此可以用较少的作动器控制较多的模态。

3 空间结构主动控制试验分析

空间杆系智能结构是由36根杆件构成，杆件主要参数如表1所示。空间模型如图1(a)所示，模型平面尺寸为300 mm×400 mm，竖向分为三层，每层高度400 mm，每个节点处附加1 kg质量作为集中荷载。结构控制流程及加载示意图详见图1(b)。选用杆件基本参数见表1。

表1 杆件主要参数

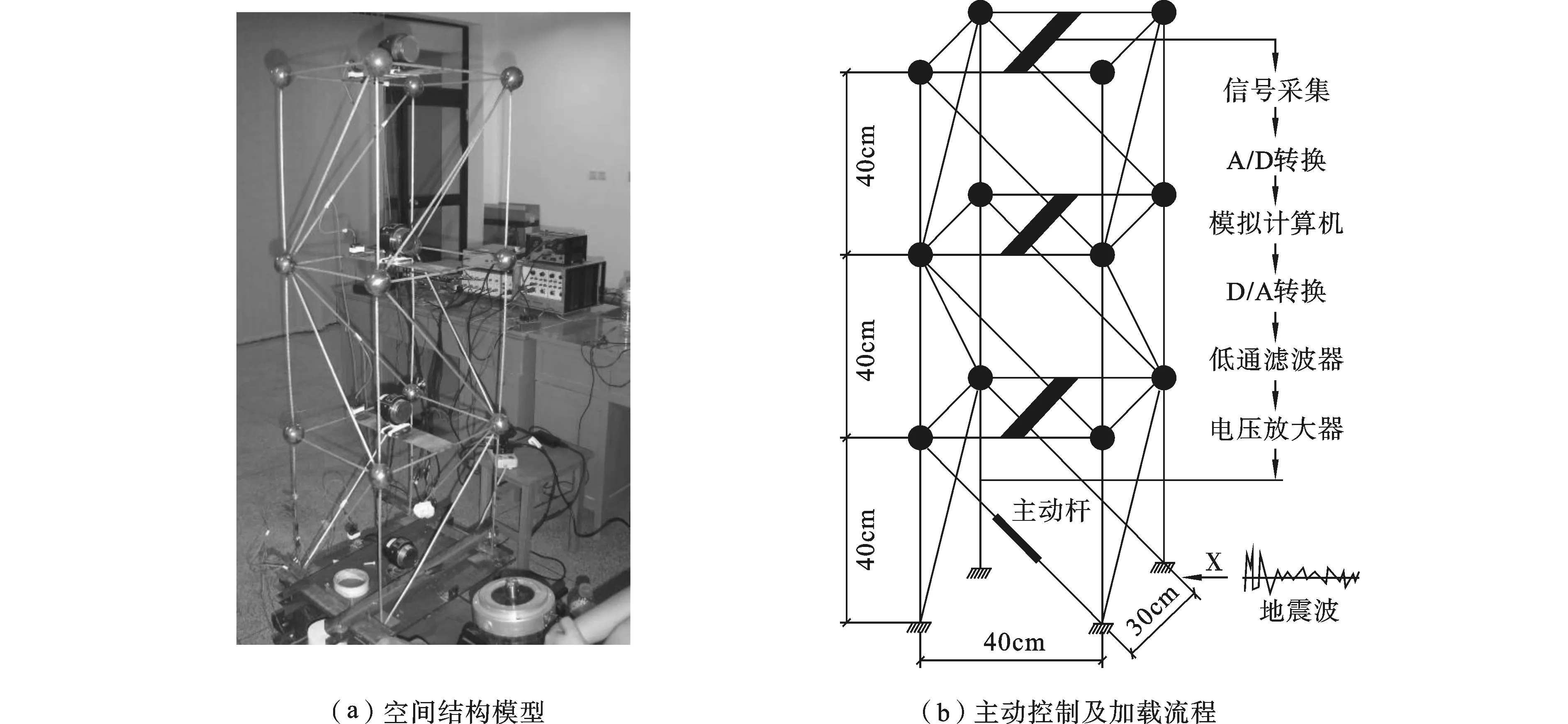
图1 空间结构智能控制试验模型

根据压电堆受压特性，压电主元杆件可以将拉力转化为压力且不承受弯矩。忽略套筒动态刚度及压电片连接部分的影响，主元杆件的有限元分析可以简化为和弹簧串联的集中质量。主元杆件及动力学模型如图2所示。压电堆的基本参数如表2所示。

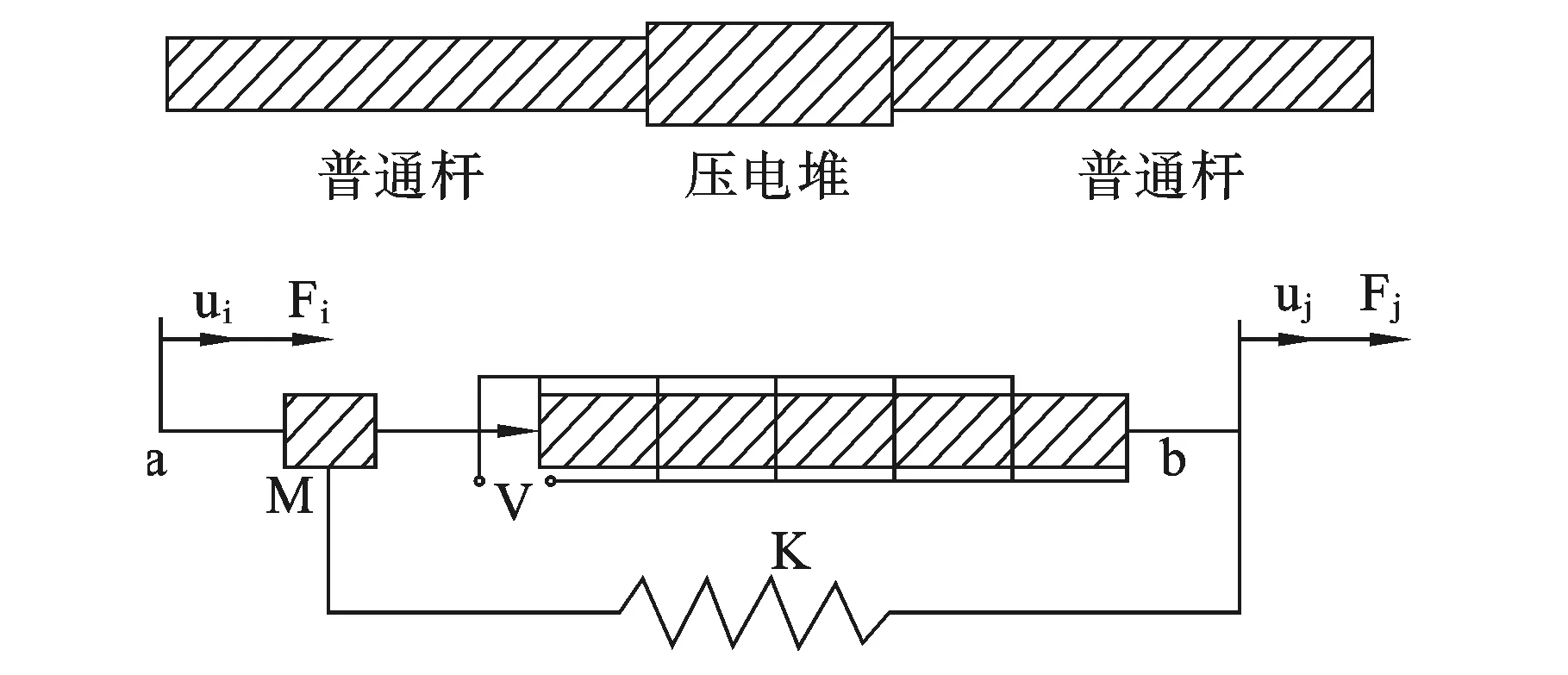
图2 压电主元杆件及计算模型

型号尺寸/mm厚度/mm片数最大电压输出力/N最大位移输出/μm等效刚度N/μm电压/V静电容/μFPTBS5×5/400.1138080052201501.60

运用一个压电堆主动杆件对结构前三阶模态进行控制, 优化设计的控制参数越大，结构反应越小[8]，同时控制力也越大，R越小，则控制力越大，结构反应越小，原则上只要满足对称半正定与正定性就可以任意选择。解代数Riccati方程后可得随主元杆件布置的性能目标函数值如表3所示，由表可知，将主元杆件布置在2号单元时，系统控制效果最好；而将主元杆件布置在33～36号杆时，控制效果最差。

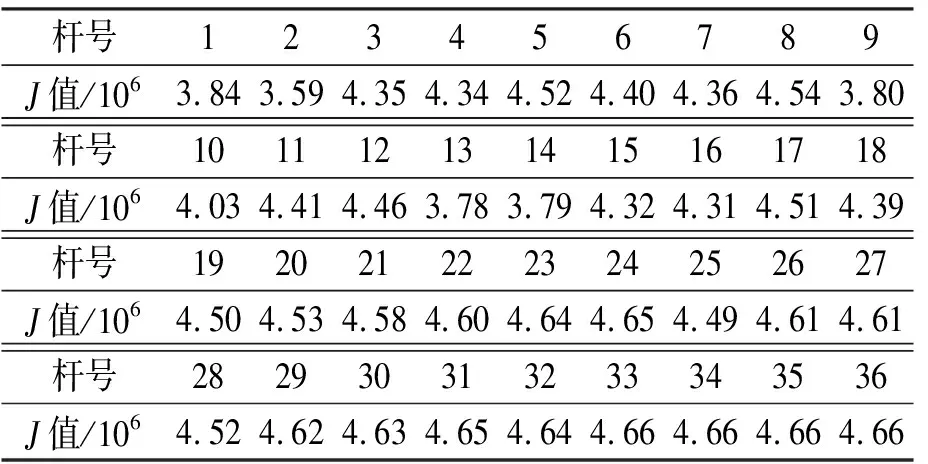
表3 主元杆件不同布置时的目标函数值

通过模态实验得到的频响函数提取出各层位移及加速度响应[9]，图3为控制前后结构每层加速度的曲线比较图，加速度峰值的最大控制量可以达到18%。图4为控制前后结构每层位移的曲线比较图，由于闭环控制作用，使得结构的峰值减小明显，最大达到12%；图5为结构一层处闭环典型频率响应函数曲线，对这些频响曲线进行拟合[9]，得到结构的闭环模态结果见表4，通过对比测试分析结果可以看到，结构的模态得到了很大程度的抑制，模态阻尼系数也得到了提高。

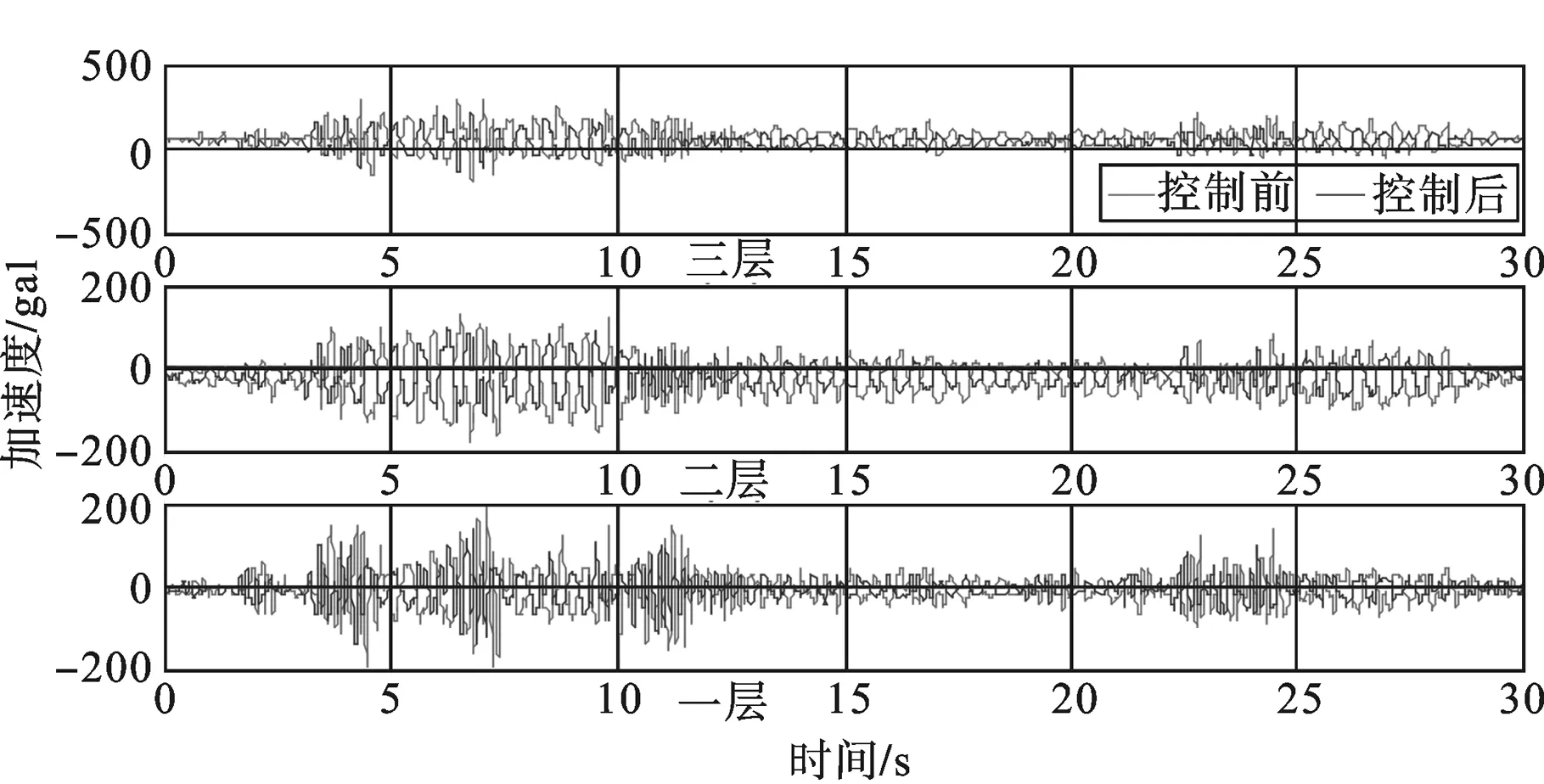
图3 各层加速度控制前后对比曲线

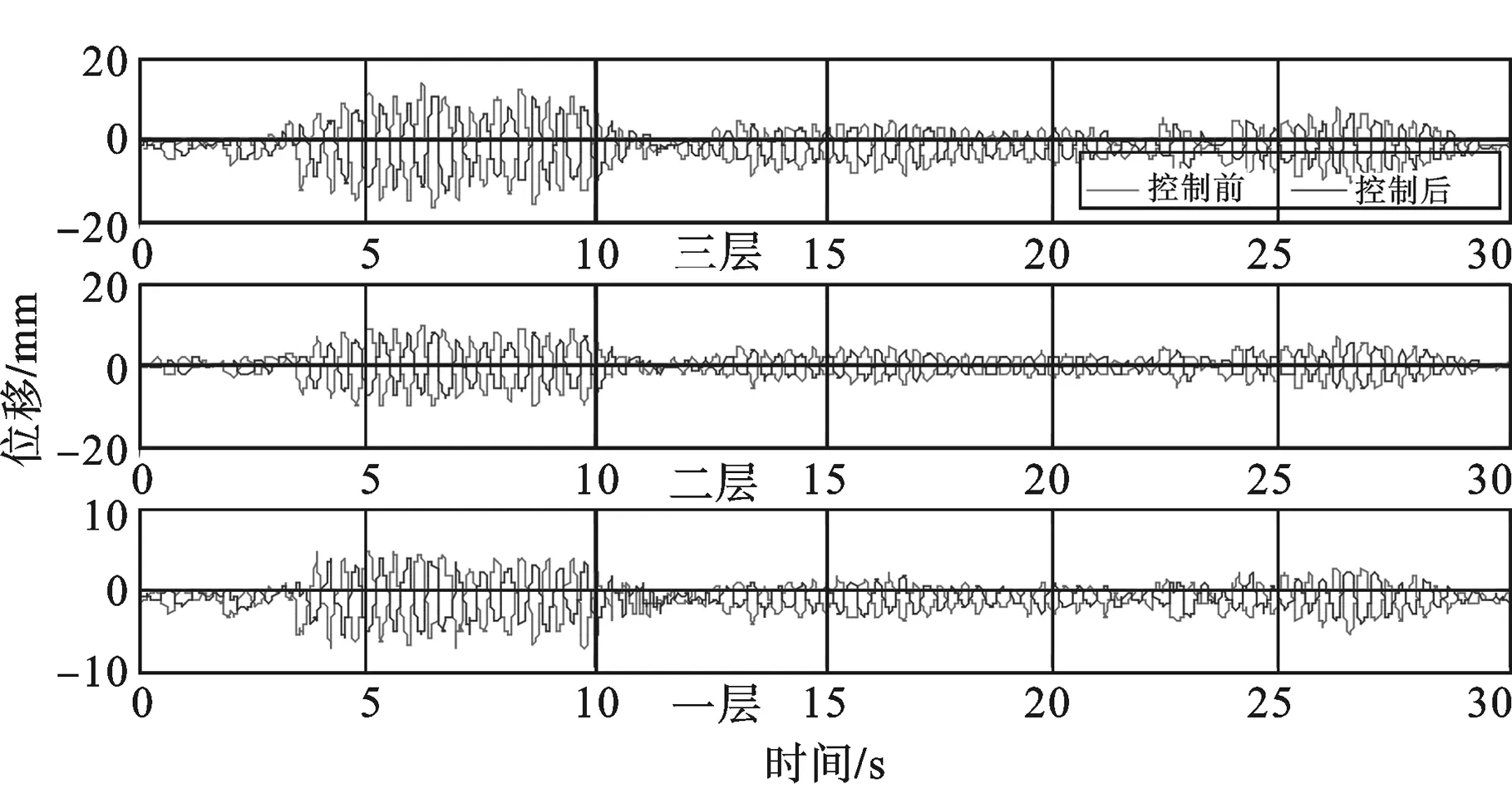
图4 各层位移控制前后对比曲线

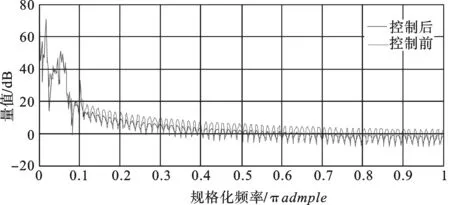
图5 控制前后结构一层响应频响曲线

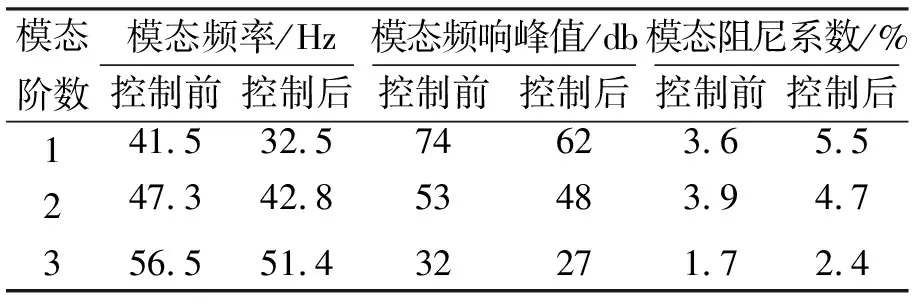
模态阶数模态频率/Hz控制前控制后模态频响峰值/db控制前控制后模态阻尼系数/%控制前控制后141.532.574623.65.5247.342.853483.94.7356.551.432271.72.4

4 结 语

本文对智能压电材料主元杆件应用到空间桁架结构中并进行了主动控制试验，依据耦合模态空间控制算法进行分析时，可以采用较少的作动器控制较多的模态，尤其主控模态接近于其他模态时有明显的效果。试验研究表明，压电主元杆件的精确传感和作动功能能够得以体现，模态阻尼得以提高。

[1]党 育,霍凯成,瞿伟廉.智能隔震结构的模态控制[J].华中科技大学学报(城市科学版), 2008,(4):130-132.

[2]胡卫兵,王骏涛.压电摩擦阻尼隔震结构地震响应及控制分析[J].振动与冲击, 2007,(2):79-83.

[3]杜永峰.滞变智能隔震结构的序列最优控制算法[J].计算力学学报,2007,(1):57-63.

[4]杜永峰.一种严密的结构最优控制极值条件及算法实现[J].工程力学,2006,(11):1-8.

[5]Spencer B F Jr, Nagarajaiah S. State of the art of structural control[J]. Journal of Structural Engineering, ASCE, 2003, 129(7): 845-856.

[6]Cho S W, Kim B W, Jung H J. Implementation of modal control for seismically excited structures using magnetorheological dampers[J]. Journal of Engineering Mechanics, 2005,131(2):177-184.

[7]Ramallo J C, Johnson E A, Spencer Jr B F, et al. Smart base isolation systems[J]. Journal of Engineering Mechanics, ASCE, 2002,128 (10):1088-1099.

[8]Agrawal A K, Xu Z, He W L. Ground motion pulse based active control of a linear base-isolated benchmark building[J] .Journal Structural Control and Health Monitoring, 2005, 13 (2-3) :792-808.

[9]马格雷伯. MATLAB原理与工程应用[M].高会生译.北京:电子工业出版社,2006.