基于神经网络和模式识别的换乘方式选择模型

覃 矞， 宗传苓

(深圳市城市交通规划设计研究中心有限公司， 广东 深圳 518034)

换乘方式选择预测是进行综合客运枢纽详细规划设计的基础性工作，一般借鉴交通方式划分模型分析思路建立换乘方式选择预测的非集计模型[1～3]。虽然，非集计模型建立在换乘效用最大化行为假说的基础上，具有较强的逻辑性。但是，人的决策过程是一个非常复杂的过程，简单的效用函数难以准确衡量人的价值取向。因此，不同乘客对不同选择肢的换乘效用是很难确定的[4]。模糊模式识别与模糊人工神经网络等人工智能方法为这一问题解决提供了良好的途径，两者结合所构造的模型，不仅具有处理不精确性和不确定性的能力，还具备学习和记忆的能力，用来模拟换乘方式选择行为是非常合适的。

根据人的决策思维过程，将换乘方式选择行为分为两个阶段，一是需求特性识别阶段，即根据个体属性与出行换乘特性找出乘客对换乘方式服务属性的要求；二是换乘方式识别阶段，即根据需求特性与各方式的服务属性寻找最佳匹配的换乘方式。在此基础上，建立基于模糊神经网络的需求特性识别以及基于模糊模式识别的换乘方式识别的两阶段换乘方式选择预测模型。

1 模型建立思路

具有不同个体属性与出行换乘特性的乘客对换乘方式服务属性的需求是不相同的，而不同的个体需求特性必定对应于一个与其匹配度最高的换乘方式。

1.1 资料调查

调查内容包括乘客个体特性与出行换乘特性问卷调查、乘客对换乘方式服务属性需求意向调查以及换乘方式服务属性调查等内容。

1.2 调查资料整理

首先将乘客的个体特性及出行换乘特性调查资料与服务属性需求意向调查资料配对，并将有效调查数据分成学习样本集与检验样本集，分别用于网络模型的学习和检验。

其次将个体特性和出行换乘特性中的连续性变量模糊化，建立相应模糊集的隶属函数[5]。

再是将个体特性和出行换乘特性中的选择性变量进行二进制编码。假设共有n种可供选择的情形，则编码位数为int[log2(n-1)+1]。

再次是建立各种服务属性的模糊集，并对每个乘客的服务属性需求意向模糊化，确定各个需求意向对相应模糊集的隶属度。

最后建立各换乘方式与服务属性模糊特征的对应规则，确定各换乘方式各种服务属性对相应模糊集的隶属度。

1.3 模型构造

首先，构造需求特性识别的模糊神经网络模型，用学习样本对网络进行学习，用检验样本对完成学习后的模型进行检验。

其次，构造换乘方式模糊识别模型，将模糊神经网络个体需求特性的输出与各换乘方式的服务属性相比较，求得相互之间的接近度，接近度归一化即可得到选择某种换乘方式的概率。

1.4 模型检验与修正

利用调查数据对模型的命中率和相对误差进行检验，并对模型进行修正，即可用于预测。

2 模型构造

2.1 需求特性识别模型

需求特性识别是根据乘客的个体属性与出行换乘特性，寻找换乘需求特性，即乘客对换乘方式服务属性的要求，可利用模糊自适应控制神经网络建立需求特性识别模型。

2.1.1网络结构

模糊自适应控制神经网络是一种前向多层网络，它把一个传统的模糊逻辑控制器的基本元件与具有分布学习能力的连接式结构结合在一起。其中，输入和输出节点分别代表输入状态和输出控制信号，隐含层节点产生隶属函数和模糊逻辑规则。本文所采用的网络是一个五层前向网络，网络结构如图1所示。

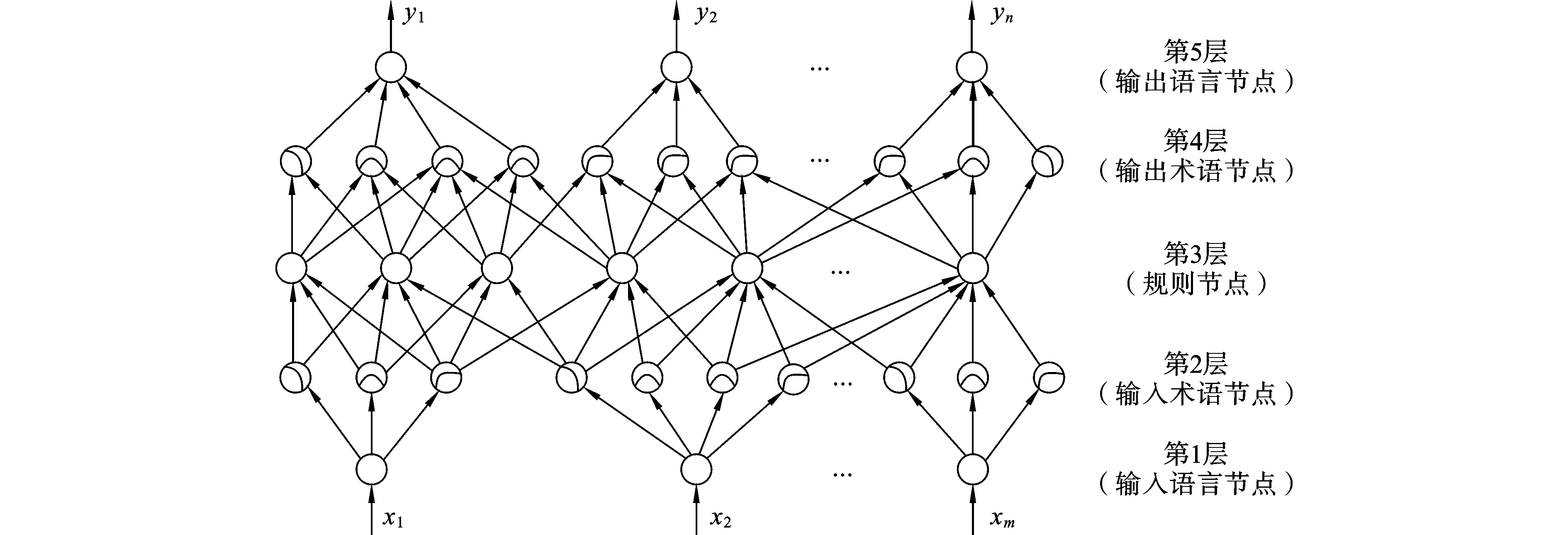
图1 模糊自适应控制网络结构

2.1.2节点定义

第一层：输入节点，接收乘客个体属性与出行换乘特性变量。节点数与所采用的个体属性及出行换乘特性的个数之和相等。该层节点只与第二层中代表与输入特性相对应的模糊集或二进制编码位的节点连接，连接权均为1.0。

第二层：术语节点，代表输入特性的模糊集或二进制编码的位，对输入进行模糊化或二进制编码。节点数为各输入特性模糊集的个数或二进制编码的位数之和。节点激活阈值为0.0，激活函数为相应模糊集的隶属度函数，或进行二进制编码和取位运算。该层节点与第三层中所有的节点连接，连接权值通过学习确定。

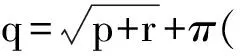
第四层：术语节点，代表服务属性需求意向模糊集，实现自上而下与自下而上两种运算模式。节点数与各种服务属性模糊集个数之和相等，且只与第五层中相对应的服务属性需求意向输出节点连接，连接权值为1.0。自上而下运算是为了在监督学习阶段服务属性理想输出的模糊化；自下而上运算用于网络的学习和预测阶段，学习阶段利用其实际输出值与理想输出值的误差来进行网络训练，预测阶段用来输出乘客对换乘方式服务属性需求意向模糊集的隶属度。节点激活函数仍采用Sigmoid型函数，激活阈值通过学习确定。

第五层：输出节点，代表乘客对服务属性的需求意向，节点数目与所采用的服务属性的数目相等。也有自上而下与自下而上两种运算模式，自下而上的传输为决策信号输出，自上而下传输训练样本的理想输出数据。该层节点主要用于网络的监督学习阶段，预测阶段已不再需要。

2.1.3学习过程算法

网络模型的学习过程就是训练第二、四层之间的连接权值以及第三、四层节点激活阈值，可采用误差反向传播算法(Error Back-Propagation Algorithm，简称BP算法)[2,7]。

2.2 换乘方式识别模型

换乘方式识别是根据换乘需求特性，计算与各换乘方式服务属性的接近度，从而得到乘客选择某种换乘方式的概率，可利用模糊模式识别技术建立换乘方式识别模型。

2.2.1换乘方式与服务属性的特征对应关系

换乘方式与服务属性的特征对应关系，就是通过专家调查或旅客问卷调查确定各换乘方式的服务属性对相应模糊集的隶属度。如采用换乘时间以及换乘方式的运营速度、费用、方便性、准时性等服务属性作为模式识别特征，可相应地划分为5个模糊集。

2.2.2换乘方式模糊识别模型

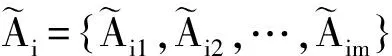
(1)

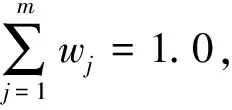
2.2.3换乘方式选择概率

(2)

3 模型检验

可以引入命中率和相对误差两个指标对模型进行检验[9]。

3.1 命中率

从非集计角度考察模型的符合程度。如果选择概率最大的换乘方式与其实际选择的换乘方式相同，则称模型对观测值是命中的。

Hi=card(Ci∩Oi)/card(Oi)×100%

(3)

式中：Hi为换乘方式i的命中率；Ci为模型测算换乘方式i概率最大的乘客个体构成的集合；Oi为观测样本中选择换乘方式i的乘客个体构成的集合；card为集合中的元素个数。

3.2 相对误差

从集计角度考察模型的符合程度：

(4)

4 实例分析

厦深铁路深圳东站是集准高速铁路、轨道交通、常规公交、出租、私人小汽车等多种交通方式于一体的综合客运枢纽(图2)[10]，现利用所建模型研究铁路旅客选择轨道交通(metro)、常规公交(bus)、出租(taxi)、私人小汽车(car)以及步行(walk)等换乘方式的概率。

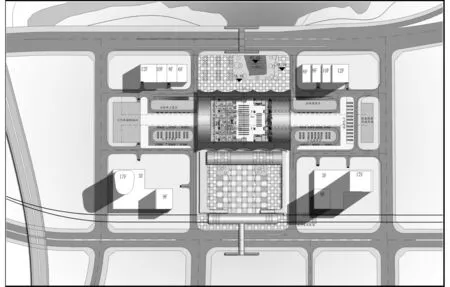
图2 厦深铁路深圳东站综合枢纽总体布局

深圳东站尚未建成，因此利用与深圳东站相似的广深准高速铁路罗湖站进行现状调查。从需求意向调查可知，乘客选择换乘方式主要考虑换乘时间(T)以及换乘方式的运营速度(V)、费用(M)、方便性(C)和准时性(R)等五种服务属性，经统计分析其权重约为wT=0.26、wV=0.14、wM=0.22、wC=0.17、wR=0.21。将上述服务属性划分为五个模糊集，利用调查数据进行需求特性识别网络模型的训练与检验，并可得到深圳准高速铁路旅客的换乘需求特性如表1所示。

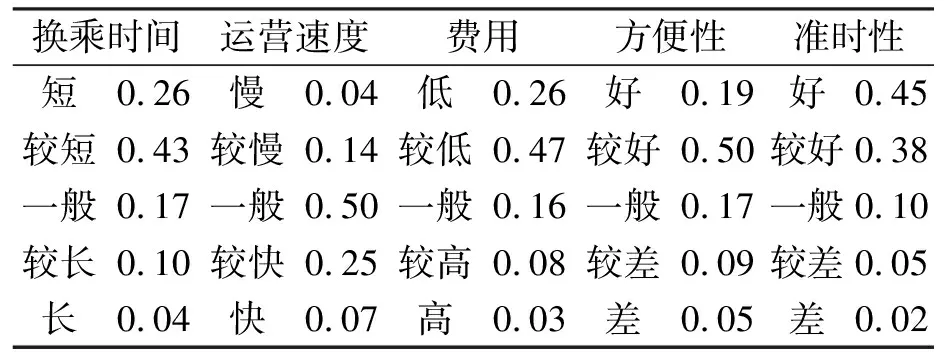
表1 深圳准高速铁路旅客换乘需求特性

根据深圳东站枢纽规划设计方案，通过专家评估建立上述五种换乘方式与服务属性的特征对应关系如表2～表6所示。

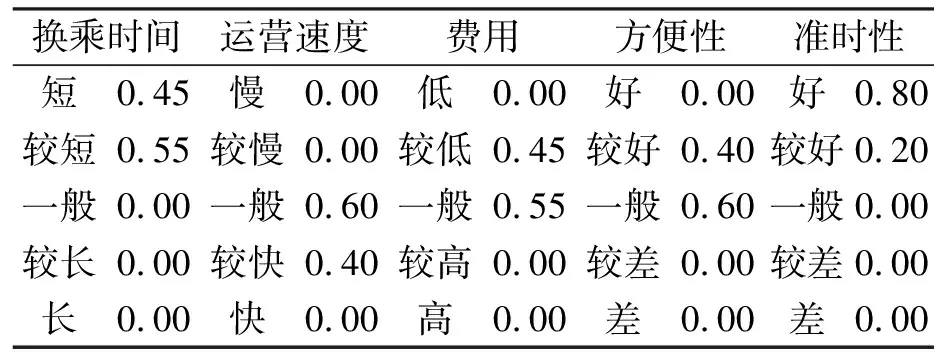
表2 轨道交通与服务属性的特征对应关系

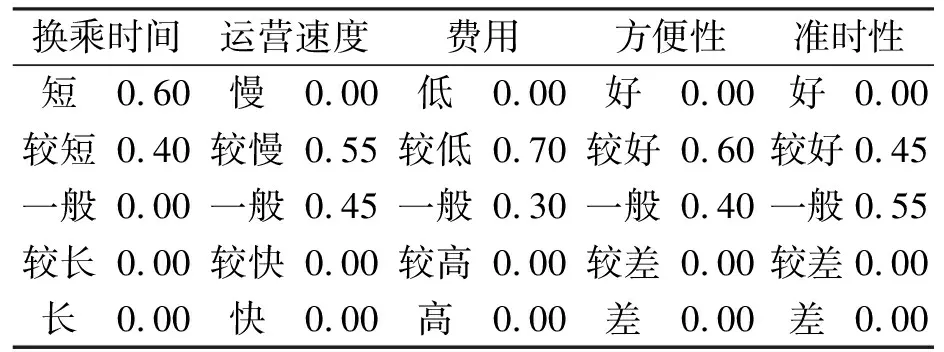
表3 常规公交与服务属性的特征对应关系

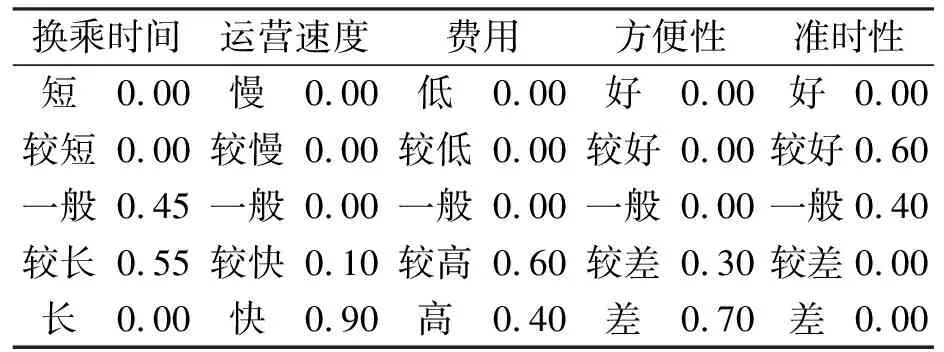
表4 出租与服务属性的特征对应关系

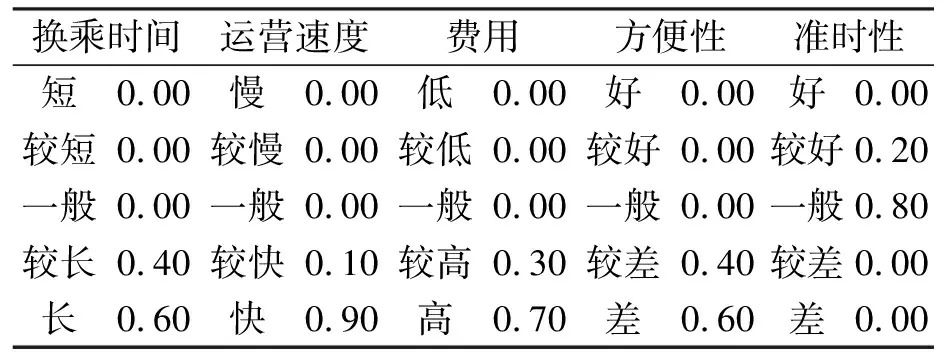
表5 私人小汽车与服务属性的特征对应关系

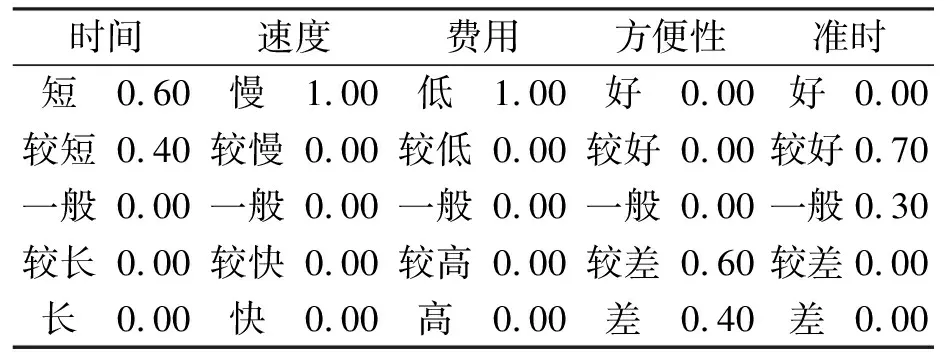
表6 步行与服务属性的特征对应关系

利用换乘方式识别模型可得到五种换乘方式与换乘需求特性的接近度,分别为N(metro)=0.45、N(bus)=0.43、N(taxi)=0.18、N(car)=0.12、N(walk)=0.27。将接近度归一化可得到铁路旅客选择换乘方式的概率，分别为P(metro)=0.308、P(bus)=0.299、P(taxi)=0.126、P(car)=0.083、P(walk)=0.184，与利用其它方法得到的换乘方式选择比例(31.7%、30.3%、12.3%、8.0%、17.7%)[10]十分接近，说明本文所建立的模型可用于综合客运枢纽的规划实践。

5 结 语

本文试图采用模糊模式识别与模糊人工神经网络等人工智能方法，从另一个角度来建立一种交通预测的非集计模型，并以厦深铁路深圳东站综合枢纽详细规划为案例，得到了铁路旅客选择各种换乘方式的概率。该方法对换乘方式选择行为具有较强的解释性，并可避免传统非集计模型效用函数难以确定的缺点，具有较好的可操作性。但是，该模型需要进行大量的数据调查，各种属性的选取还需根据规划城市的实际情况进行深入的研究。从建模过程来看，该模型不仅可以用于换乘方式选择预测，也可用于出行方式划分预测。

[1]陆化普. 交通规划理论与方法[M]. 北京:清华大学出版社, 1998.

[2]覃 矞. 轨道交通枢纽规划与设计理论研究[D]. 上海: 同济大学, 2002.

[3]何 明, 过秀成, 冉江宇, 等. 基于非集计MNL模型的轨道交通方式预测[J]. 交通运输系统工程与信息, 2010, 10(2): 136-142.

[4]David A Hensher, Tu T Ton. A comparison of the predictive potential of artificial neural networks and nested logit models for commuter mode choice[J]. Transportation Research Part E: Logistics and Transportation Review, 2000, 36(3): 155-172.

[5]杨纶标, 高英仪. 模糊数学原理及应用[M].广州: 华南理工大学出版社, 2001.

[6]赵振宇. 模糊理论和神经网络的基础和应用[M]. 北京: 清华大学出版社, 1993.

[7]王 旭, 王 宏. 人工神经元网络原理与应用[M]. 沈阳: 东北大学出版社, 2000.

[8]Timothy J Ross. 模糊逻辑及其工程应用[M]. 钱同惠译. 北京: 电子工业出版社, 2001.

[9]贾俊刚, 杨东援. 基于概率神经网络的交通方式划分模型[J]. 上海理工大学学报, 1999, 21(1): 9-12.

[10]宗传苓, 覃 矞, 龙俊仁, 等. 厦深铁路深圳东站客运枢纽综合规划[R]. 深圳: 深圳市城市交通规划设计研究中心有限公司, 2008.