双向增强体复合地基工作性状的时效性研究

陈保国， 郑俊杰

(1. 中国地质大学 a.岩土钻掘与防护教育部工程研究中心； b.工程学院， 湖北 武汉 430074；2. 华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

1 概 述

双向增强体复合地基是由水平向加筋材料和竖向桩体两部分协同工作形成的人工地基，其工作性状复杂，影响因素众多[1,2]。工作性状不仅与材料的性质和参数有关，而且还与时间因素有关[3]。宴莉等(2005)分析了桩承式土工合成材料加筋垫层的工作原理及其应用情况[4]。陈仁朋等(2005)采用单桩加固范围内的圆柱体作为分析单元，利用数值模拟研究了桩承式加筋路堤的受力机理和沉降特性[5]。陈艳平等(2006)利用模型试验分析了土工格室碎石垫层与碎石桩组成的复合地基的承载力和沉降变形机理[6]。Abdullah & Edil(2007)结合现场测试分析了采用土工格栅和碎石桩加固路基的荷载传递机理[7]。赵明华等(2008)结合理论分析得出了双向增强体复合地基工后沉降的计算方法[8]。Chen(2008)通过室内模型试验分析了桩承式加筋路堤填土中的土拱效应[9]。

笔者曾对双向增强体复合地基中的水平向筋材、桩体、桩间土之间的作用机理进行了系统研究，并对其工作性质的影响因素进行了分析[10～12]，同时对其时效性展开了初步的研究工作[13]。目前的研究工作主要基于荷载传递机理的研究，而很少深入分析双向增强体复合地基工作性状随时间的变化规律，而且没有考虑加载方案的影响。

为了进一步完善双向增强体复合地基的计算理论，本文通过有限元数值模拟研究四种典型情况下双向增强体复合地基工作性状随时间的变化规律：

Case-1：桩端穿透软弱土层，路堤填土采用瞬时加载方案；

Case-2：桩端穿透软弱土层，路堤填土采用分步加载方案；

Case-3：桩端未穿透软弱土层，路堤填土采用瞬时加载方案；

Case-4：桩端未穿透软弱土层，路堤填土采用分步加载方案。

探索软土地基中超静孔隙水压力的分布和消散规律，以期为双向增强体复合地基的设计和施工提拱参考。

2 数值分析

2.1 有限元模型

有限元模型中路堤填土高度6 m，路堤顶面宽度24 m，路堤边坡坡率为1∶1.75。地基土表层为厚度0.5 m左右的覆盖层，施工时将表层清除，中间层为厚度30 m左右的饱和软土层，下卧层为强风化泥岩。软土地基中采用水泥土搅拌桩连续施工形成桩墙，宽度为0.5 m，中心间距为2.0 m，桩长分别选用30 m和20 m两种型式，即一种穿透软土层，另一种未穿透软土层。桩墙顶面设置0.5 m厚的砂垫层，垫层上铺设单层高强土工格栅，计算模型的底面取至强风化泥岩顶面，如图1所示。

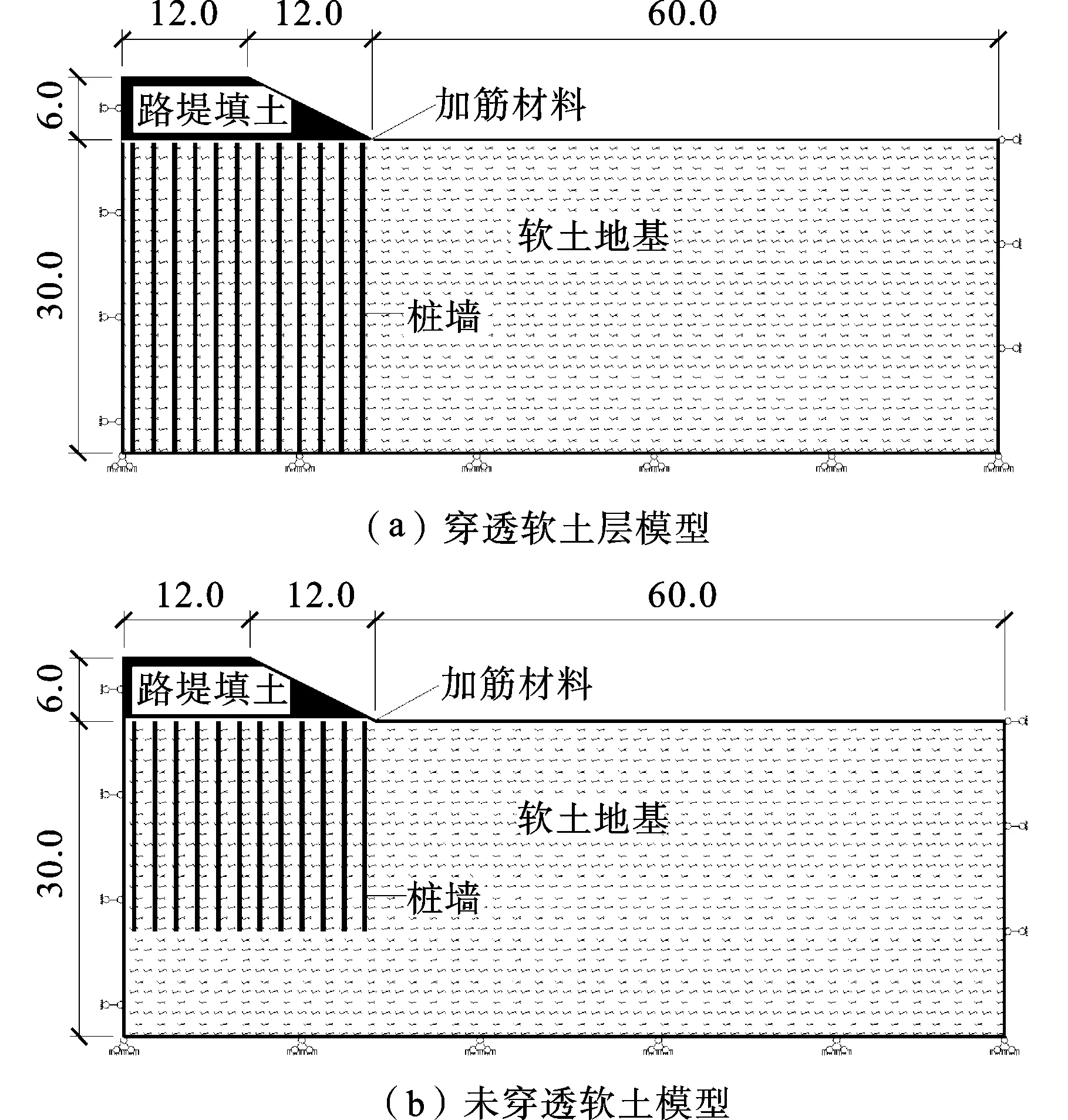
图1 有限元计算模型/m

2.2 模型的边界条件和网格单元

模型的位移边界条件：模型两侧只约束水平向位移，允许产生竖向位移；模型底部设水平向和竖向约束。模型的排水边界条件：模型两侧和底边界的固结排水条件封闭，上边界为自由排水边界。

模型网格划分时，路堤和地基采用15节点三角形高精度单元，桩体采用梁单元，筋材采用与15节点相对应的5节点格栅单元。桩体-桩间土-筋材-路堤填土之间的界面接触采用相应的5节点接触单元，界面单元的刚度矩阵由Newton-Cotes积分得到。当界面处于弹性状态时，界面剪应力为：

|τ|<σntanφi+ci

(1)

当界面处于塑性状态时，界面剪应力为：

|τ|=σntanφi+ci

(2)

式中：σn和τ分别为作用于界面上的正应力和剪应力；φi和ci分别为界面的内摩擦角和黏聚力，它们由相应的土体的强度参数折减得到：

ci=Rintercsoil

(3)

tanφi=Rintertanφsoil≤tanφsoil

(4)

式中：Rinter为界面强度折减系数。当界面材料完全粘结时，Rinter取1.0；当界面完全光滑时，Rinter取0.0。根据相应的试验结果和工程经验，数值模拟中路堤填土及垫层与桩体之间的Rinter取0.8，黏土与桩体之间的Rinter取0.5[14]。

2.3 材料模型

路堤填料为黏粒含量为10%左右的碎石土，地基土为饱和黏性土，超固结比约为2.0。模型中路堤填土、地基土和砂垫层均选用M-C屈服准则，水泥土搅拌桩墙和筋材的材料模型为线弹性，筋材的自重忽略不计。文中材料参数通过现场原位勘察和室内试验得到，具体参数见表1。

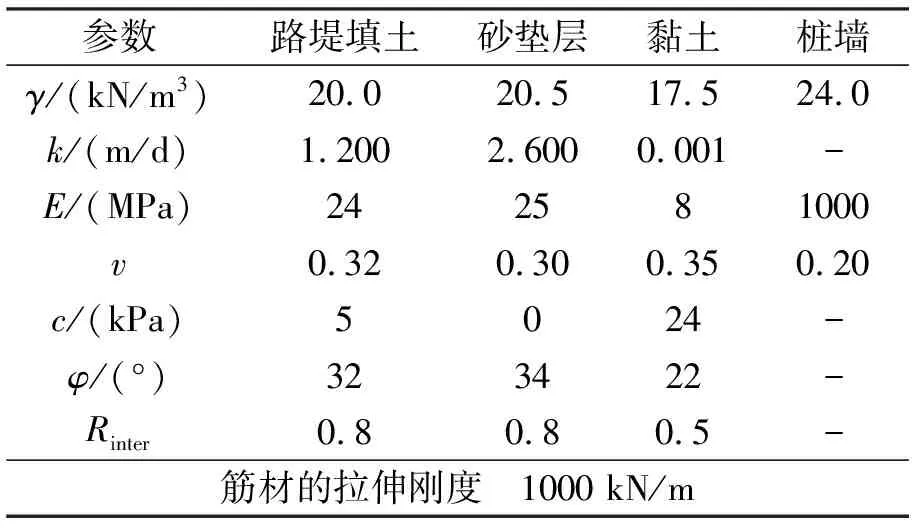
表1 数值模拟中材料参数

2.4 模拟过程

基于上述的计算模型、边界条件及材料模型，利用数值模拟分析双向增强体复合地基中的孔隙水压力、位移及受力特性随时间的变化规律。由于路堤填土为无限长的带状构造物，水泥土搅拌桩连续施工形成桩墙，故本文采用平面应变模型，利用PLAXIS软件对双向增强体复合地基的四种典型情况分别进行讨论，来反映双向增强体复合地基工作性状随时间的变化规律。路堤填土加载方案分两种，第一种方案为瞬时加载；第二种方案为分步加载，路堤填筑速度为0.1 m/d，加载方案如图2所示。

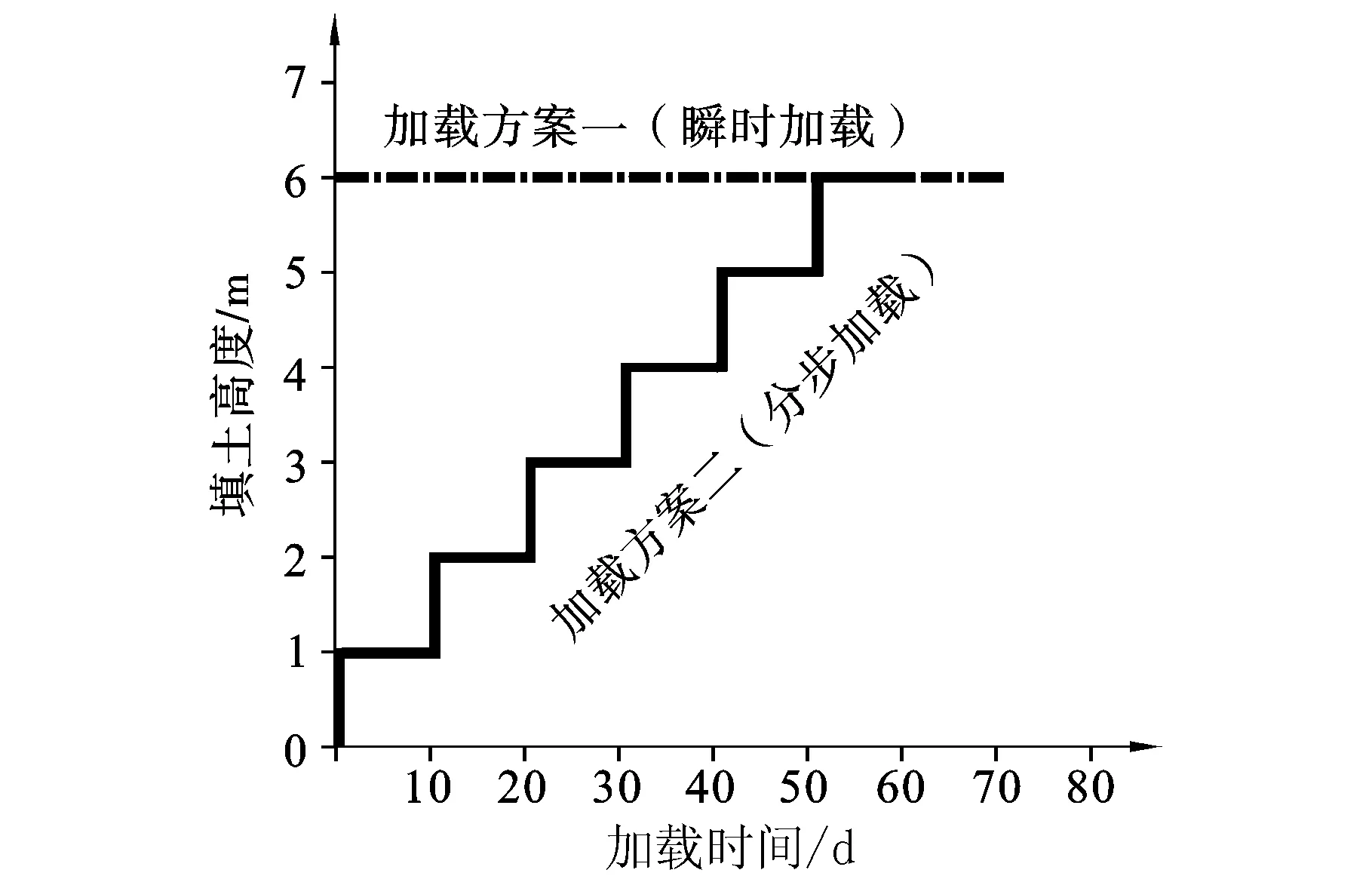
图2 加载方案

双向增强体复合地基固结分析中的控制方程采用Biot固结理论，假设地下水的渗流满足达西定理，并且土体的变形为小变形。根据Terzaghi有效应力原理，总应力由有效应力和孔隙水压力两部分组成：

(5)

(6)

3 计算结果分析

3.1 超静孔隙水压力分布及变化规律

3.1.1超静孔隙水压力分布规律

Case-1中，加载完毕时软基中最大超静孔隙水压力出现在路堤底面中间位置，沿地基深度逐渐递减(如图3所示)。最大超静孔隙水压力为62.4 kPa，该值远小于路堤的填土荷载。主要由于桩端落在较好的持力层上，大部分路堤荷载直接通过桩墙传递到持力层，减小了软基中的附加应力。当固结时间达到755 d，软基中最大超静孔隙水压力小于1.0 kPa。

Case-2中，加载完毕时软基中超静孔隙水压力分布规律与Case-1相似(如图4所示)。但其最大超静孔隙水压力只有16.4 kPa，主要原因是：(1)路堤分阶段填筑，填土过程中伴随着超静孔隙水压力的消散；(2)大部分路堤填土荷载直接通过桩墙传递到持力层，使软基中的附加应力减小。当固结时间达到709 d时，最大超静孔隙水压力小于1.0 kPa。Case-2中产生的最大超静孔隙水压力为Case-1的26.3%。

Case-3中，加载完毕时软基中最大超静孔隙水压力出现在桩端附近的区域(如图5所示)，最大超静孔隙水压力达到118.5 kPa。路堤的底面处，也出现了较大的超静孔隙水压力。在桩墙中间位置处，超静孔隙水压力相对较小。Case-3中的最大超静孔隙水压力要远大于Case-1和Case-2，主要由于Case-3中桩端处于软土层中，路堤填土的大部分荷载通过桩墙传递到桩端，桩端区域附加应力明显增大，导致桩端超静孔隙水压力显著上升。当固结1534 d后，最大超静孔隙水压力小于1.0 kPa。

Case-4中，加载完毕时软基中最大超静孔隙水压力出现在桩端附近的区域(如图6所示)，最大超静孔隙水压力为57.7 kPa。该值远小于Case-3中的最大超静孔隙水压力，路堤底面处超静孔隙水压力也小于Case-3中路堤底面处的超静孔隙水压力。主要是因为路堤填土分步填筑，填筑过程中伴随着超静孔隙水压力消散。当固结时间达到1231 d时，软基中最大超静孔隙水压力小于1.0 kPa。

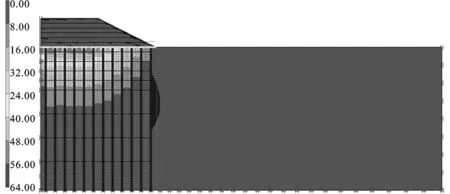
图3 超静孔隙水压力分布规律Case-1 (单位：kPa)

图4 超静孔隙水压力分布规律Case-2 (单位：kPa)

图5 超静孔隙水压力分布规律Case-3 (单位：kPa)

图6 超静孔隙水压力分布规律Case-4 (单位：kPa)

3.1.2超静孔隙水压力变化规律

四种情况下，双向增强体复合地基中最大超静孔隙水压力随固结时间的变化规律如图7所示，最大超静孔隙水压力发生的位置见上节所述。由图7可知，相同的桩端土层条件下，采用瞬时加载方案时，地基中最大超静孔隙水压力远大于采用分步加载方案时的最大超静孔隙水压力。相同的加载方案下，当桩端穿透软土层时，地基中的最大超静孔隙水压力远小于未穿透软土层情况。假设软土地基中最大超静孔隙水压力小于1.0 kPa时固结完成，那么从固结时间上看，采用分步加载方案的固结时间比瞬时加载方案的固结时间短，桩墙穿透软土层情况下的固结时间远小于未穿透软土层时的固结时间。

图7 最大超静孔隙水压力随时间的变化规律

3.2 位移时效性分析

四种情况下，路堤坡脚处最大水平位移随固结时间的变化规律如图8所示。当桩端穿透软土层时，路堤坡脚的最大水平位移随固结时间增长而增大，而未穿透软土层时，最大水平位移随固结时间增长而减小，最终都趋于稳定。主要原因是，桩端未穿透软土层时，路堤大部分荷载通过桩墙传递到桩端土层，固结过程中桩端土层超静孔隙水压力消散，桩端范围的土体产生竖向沉降和向外的水平位移，使路堤产生向内收缩的趋势。此外，由图8可知，桩端穿透软土层时路堤的最终水平位移小于桩端未穿透软土层情况下的水平位移；采用分步加载方案时路堤的工后水平位移小于瞬时加载方案的工后水平位移。

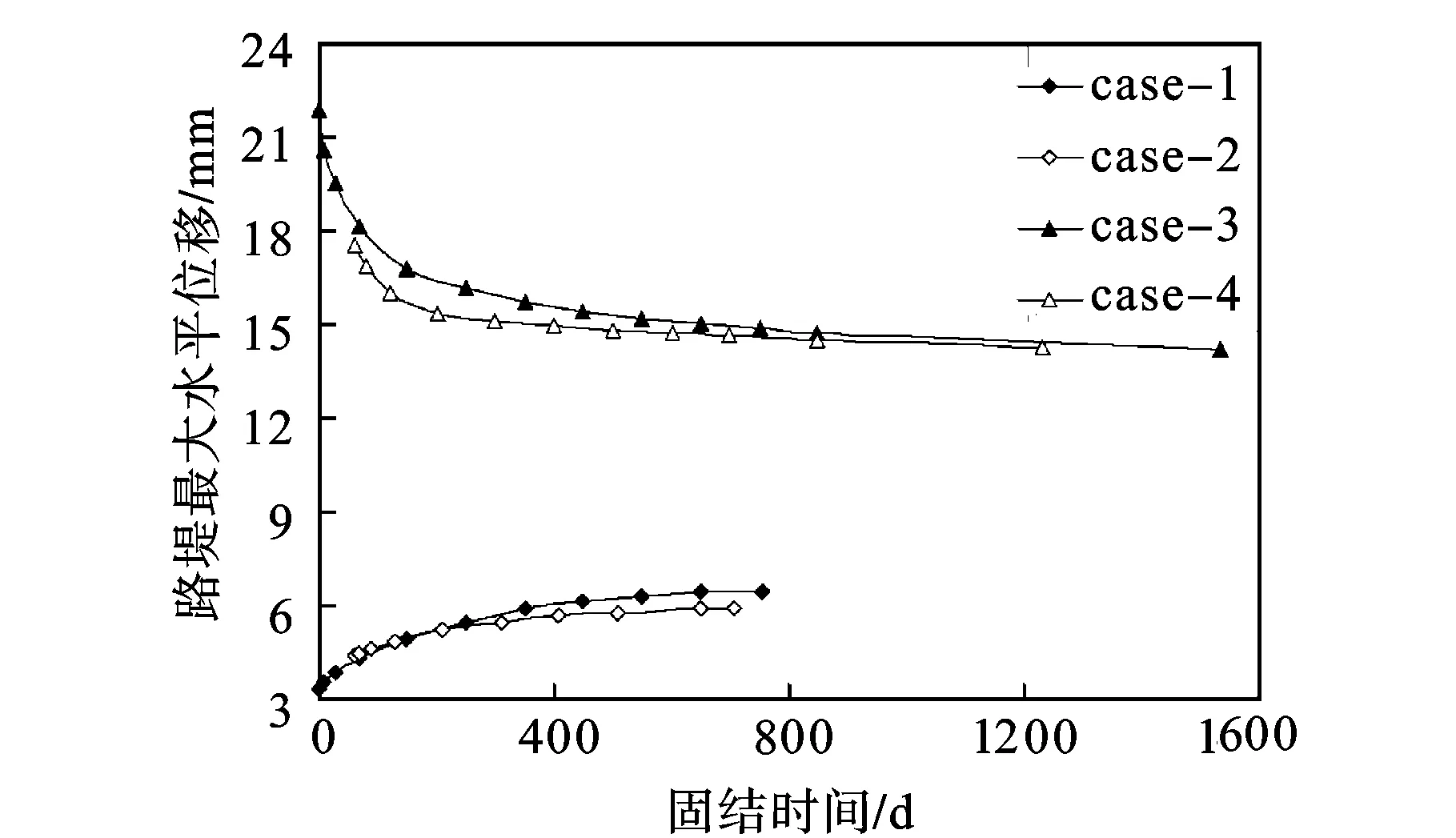
图8 路堤最大水平位移随时间的变化规律

路堤顶面中心处的最大沉降随固结时间的变化规律如图9所示。路堤最大沉降随固结时间的延长而增大，最终趋于稳定。无论采用何种加载方案，桩端未穿透软土层时路堤的沉降远大于穿透软土层时路堤的沉降。当桩端穿透软土层时，Case-2的工期沉降大于Case-1的工期沉降，但是其工后沉降小于Case-1的工后沉降。当桩端未穿透软土层时，Case-3和Case-4的最终沉降相差不大，但是Case-3的工后沉降大于Case-4的工后沉降。

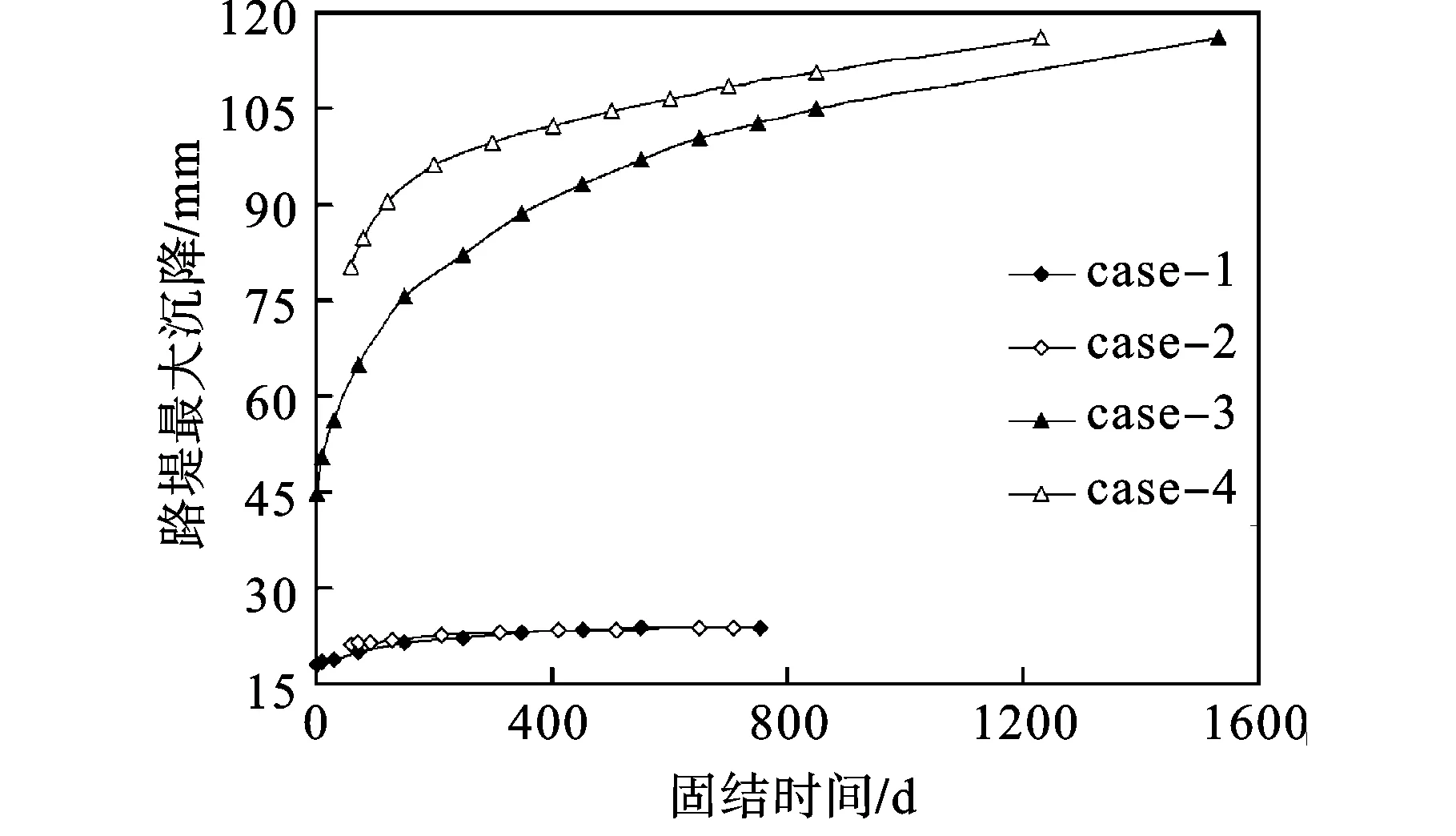
图9 路堤最大沉降随时间的变化规律

图10 桩顶平面差异沉降随时间的变化规律

桩顶平面的差异沉降随固结时间的变化规律如图10所示，该差异沉降为路堤中心处筋材的最大竖向位移与相邻桩顶的竖向位移之差。Case-1和Case-2中，桩顶平面的差异沉降均随着固结时间的增长而增大，最终趋于稳定。Case-3和Case-4中，桩顶平面的差异沉降随着固结时间的延长呈先减后增的变化趋势。主要是因为加载完毕时，大部分荷载由桩墙传递到桩端土层，桩端产生很高的超静孔隙水压力，孔隙水压力消散初期，桩端产生的刺入变形量大于桩间土的固结沉降，桩顶平面的差异沉降减小；当固结时间继续增长，桩端部分的正摩阻力增大，此后桩间土产生的固结沉降大于桩端产生的刺入变形的增量，桩顶平面的差异沉降增大。由图10可知，加载方案对桩顶平面的最终差异沉降影响不大，但是分步加载方案的工后差异沉降比瞬时加载方案的工后差异沉降小。

桩端穿透软土层时，桩墙两侧沿桩长分布的摩擦力均为负摩阻力，中性点在桩端处。当桩端未穿透软土层时，中性点位置随固结时间的变化规律如图11所示(图中为中性点深度，为桩长)。由图11可知，中性点深度随着固结时间的增长而上下波动，最终趋于稳定。两种加载方案下，中性点最终位置相差不大，均在0.35左右。加载完毕时，桩端孔压较大，随着孔隙水压力消散，桩端产生向下的刺入变形，桩端刺入量大于桩间土的固结沉降，中性点位置逐渐变浅，桩端区域正摩阻力增加；随着超静孔隙水压力进一步消散，此后桩端刺入量逐渐小于桩间土的固结沉降，此时，桩顶部分的负摩阻力增加，中性点位置变深；如此反复，桩墙受力最终达到平衡，中性点位置趋于稳定。

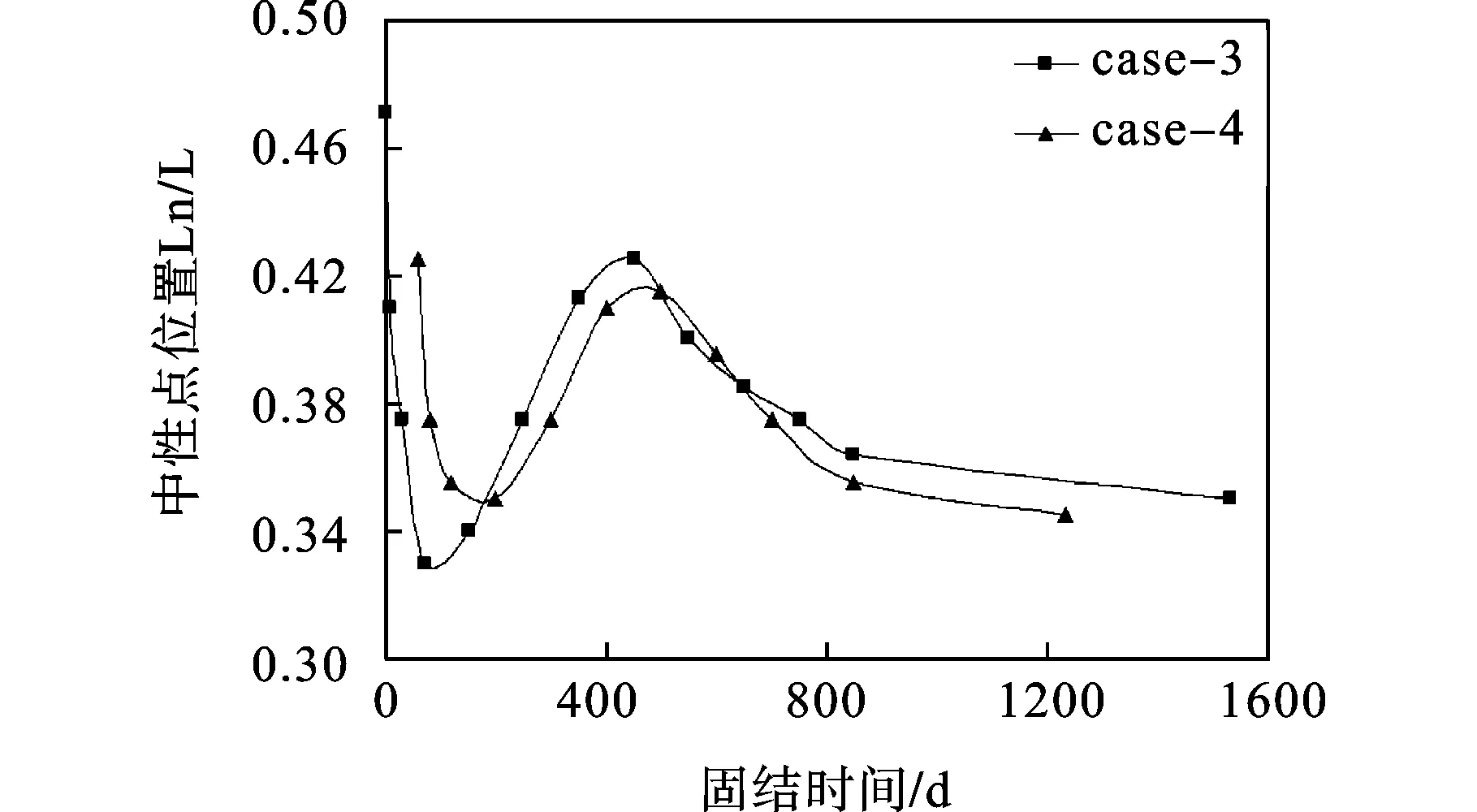
图11 中性点位置随时间的变化规律

3.3 应力时效性分析

桩端穿透软土层时，筋材最大拉力随固结时间的增长而增大。桩端未穿透软土层时，筋材最大拉力随固结时间的增长呈先增后减变化趋势，最终趋于稳定(如图12所示)。主要由于固结初期，桩端产生刺入变形，路堤侧向位移主要靠筋材摩阻力来约束，故筋材拉力出现增大趋势。但是随着时间的增长，桩端超静孔隙水压力消散，桩端产生向外的水平位移，路堤水平位移有向内收缩的趋势，因而筋材拉力又随之减小。这种变化规律正好与路堤水平位移的变化规律相吻合。计算结果表明，加载方案(Case-1与Case-2，或Case-3与Case-4)对筋材的最终拉力的影响不大，而桩端地基土的性质对筋材拉力的影响较大。

图12 筋材的最大拉力随时间的变化规律

路堤中心处桩墙最大轴力随固结时间的变化规律如图13所示。Case-1和case-2中，桩墙最大轴力随固结时间的增长而增大，两者的最终轴力相差不大。但加载完毕时，分步加载方案的桩墙轴力大于瞬时加载方案得到的轴力，主要由于加载过程中，桩间土发生固结沉降，桩墙负摩阻力增加。Case-3和Case-4中，桩墙最大轴力随时间的增长呈先减后增的变化趋势，主要由于固结初期，桩端超静孔隙水压力消散，桩端产生较大的固结沉降，导致轴力减小，此后，随着时间的增长，桩端刺入量小于桩间土的固结沉降，一方面，桩墙上部负摩阻力增加，另一方面，桩顶平面差异沉降增大，路堤填土荷载通过筋材的张力膜效应和土拱效应传递到桩顶，引起桩墙轴力增大。

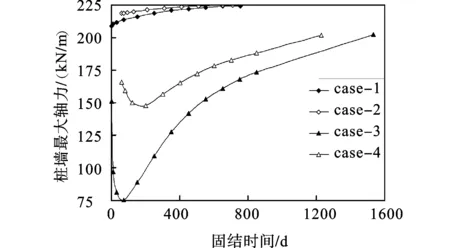
图13 桩墙最大轴力随时间的变化规律

四种情况下，路堤中心处桩墙的荷载分担比随时间的变化规律如图14所示，该荷载分担比定义为路堤纵向每延米桩墙范围内，桩顶的轴力与该桩墙分担的面积上的填土自重之比。由图14可知，当桩端穿透软土层时，桩墙的效率随时间的增长而增大，两种加载方案下，最终桩墙的效率相差不大。当桩端未穿透软土层时，桩墙的效率随时间的增长呈先减后增的变化趋势。桩端穿透软土层时，桩墙的荷载分担比大于桩端未穿透软土层时的桩墙荷载分担比。

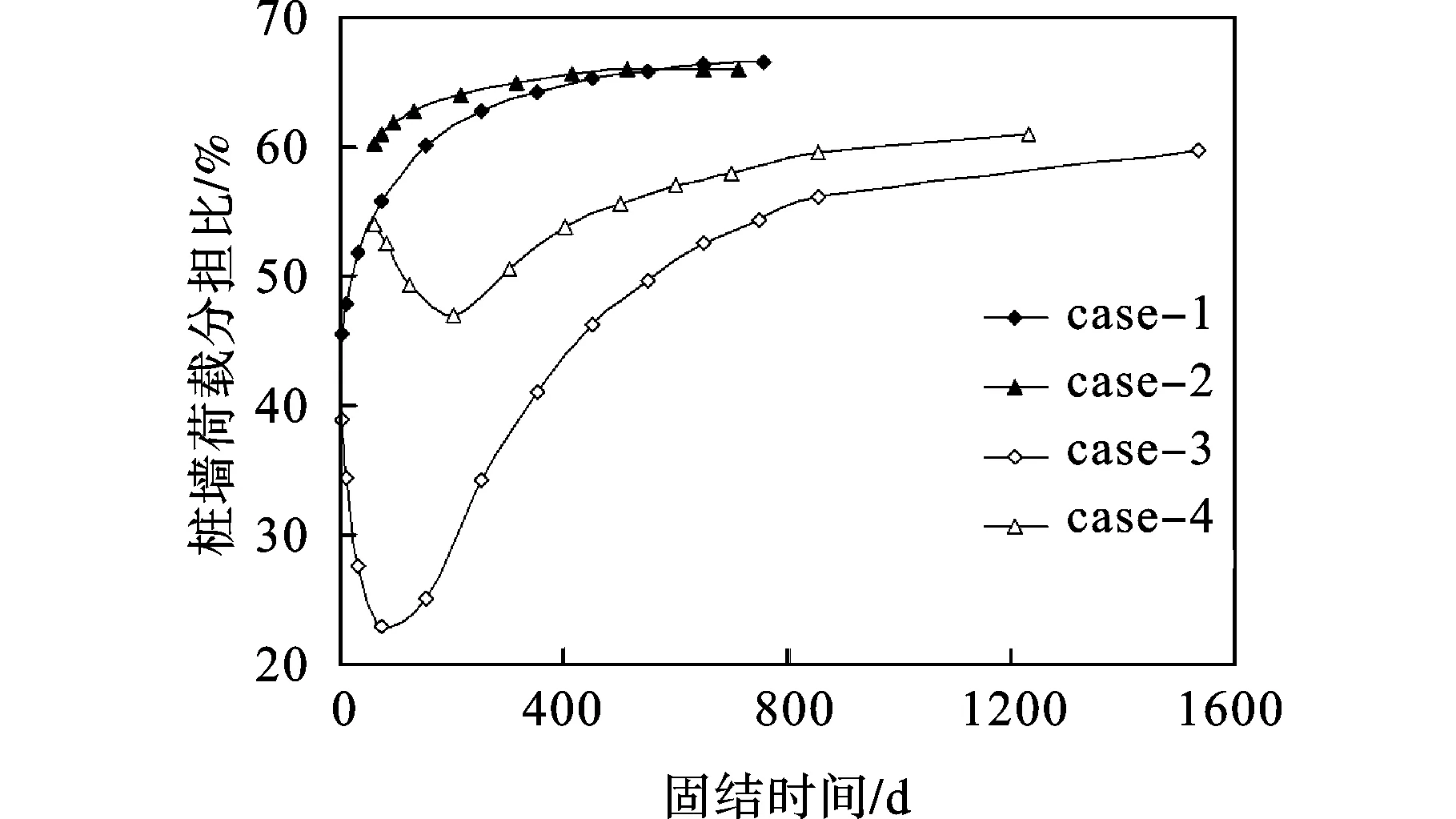
图14 桩墙荷载分担比随时间的变化规律

4 结 论

(1)桩端穿透软土层情况下，加载完毕时软基中最大超静孔隙水压力出现在路堤底面处，超静孔隙水压力沿深度呈递减趋势；桩端未穿透软土层时，加载完毕时软基中最大超静孔隙水压力出现在桩端附近的土层中。相同的桩端土层条件下，瞬时加载方案产生的最大超静孔隙水压力远大于分步加载方案产生的最大超静孔隙水压力。相同的加载方案下，桩端穿透软弱土层时，软基中的最大超静孔隙水压力远小于未穿透软土层情况。分步加载方案的固结时间比瞬时加载方案的固结时间短，桩端穿透软土层时的固结时间远小于未穿透软土层时的固结时间。

(2)桩端穿透软土层时，路堤坡脚的最大水平位移随固结时间增长而增大；未穿透软土层时，随固结时间的增长而减小，最终趋于稳定。桩端穿透软土层时路堤的最终水平位移小于桩端未穿透软土层情况下的最终水平位移；采用分步加载方案时路堤的工后水平位移小于瞬时加载方案的工后水平位移。

(3)桩端穿透软土层时，桩顶平面的差异沉降随着固结时间的增长而增大；未穿透软土层时，桩顶平面的差异沉降随着固结时间的增长呈先减后增的变化趋势。加载方案对路堤的最终沉降和桩顶平面的最终差异沉降量影响不大，但是瞬时加载方案得到的工后沉降和工后差异沉降比分步加载方案大。

(4)桩端未穿透软土层时，中性点位置随着固结时间的增长而上下波动，并最终趋于稳定，两种加载方案下，中性点最终位置相差不大。

(5)桩端穿透软土层时，筋材最大拉力和路堤中心处桩墙最大轴力随固结时间的增长而增大；桩端未穿透软土层时，筋材最大拉力随固结时间的增长呈先增后减的变化趋势，桩墙最大轴力呈先减后增的变化趋势，最终趋于稳定。加载方案对筋材最终拉力和桩墙的最终轴力影响不大。桩墙荷载分担比随时间的变化规律与桩墙轴力的变化规律相似。

[1]Han J, Gabr M A. Numerical analysis of geosynthetic- reinforced and pile-supported earth platforms over soft soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(1): 44-53.

[2]陈保国, 郑俊杰, 骆瑞萍，等. 双向增强体复合地基作用机理研究[J]. 湖南大学学报(自然科学版), 2008, 35(11): 318-323.

[3]Liu S Y, Han J, Zhang D W, et al. A combined DJM-PVD method for soft ground improvement[J]. Geosynthetics International, 2008, 15(1): 43-54.

[4]晏 莉, 阳军生, 韩 杰. 桩承土工合成材料加筋垫层复合地基作用原理及应用[J]. 岩土力学, 2005, 26(5): 821-826.

[5]陈仁朋, 贾 宁, 陈云敏. 桩承式加筋路堤受力机理及沉降分析[J]. 岩石力学与工程学报, 2005, 24(23): 4358-4367.

[6]陈艳平, 赵明华, 陈昌富，等. 土工格室碎石垫层-碎石桩复合地基相似模型试验[J]. 中国公路学报, 2006, 19(1): 17-22.

[7]Abdullah C H, Edil T B. Behaviour of geogrid- reinforced load transfer platforms for embankment on rammed aggregate piers[J]. Geosynthetics International, 2007, 14(3): 141-153.

[8]赵明华, 刘敦平, 张 玲. 双向增强体复合地基工后沉降分析[J]. 公路交通科技, 2008, 25(10): 26-30.

[9]Chen Y M, Cao W P, Chen R P. An experimental investigation of soil arching within basal reinforced and unreinforced piled embankments[J]. Geotextiles and Geomembranes, 2008, 26(2): 164-174.

[10]郑俊杰, 陈保国, Abusharar S W等. 双向增强体复合地基桩土应力比分析[J]. 华中科技大学学报(自然科学版), 2007, 35(7): 110-113.

[11]Abusharar W S, Zheng J J, Chen B G. A simplified method for analysis of a piled embankment reinforced with geosynthetics[J]. Geotextiles and Geomembranes, 2008, 26(5): 39-52.

[12]Chen B G, Zheng J J, Abusharar S W, et al. Theoretical study and numerical analysis on geosynthetic reinforced and pile wall supported embankment[C]//Proceeding of the 4th Asian Regional Conference on Geosynthetics, Zhengjiang University and Springer Press, Shanghai, 2008: 709-717.

[13]Zheng J J, Chen B G, Lu Y E. The performance of an embankment on soft ground reinforced with geosynthetics and pile walls[J]. Geosynthetics International, 2009, 16(3): 173-182.

[14]Brinkgreve R B J，Vermeer P A. Finite Element Code for Soil and Rock Analysis[M]. Rotllendan: A. A. Balkema, 1998.