BP神经网络在城市房屋拆迁估价中的应用

王军武， 林 晶

(武汉理工大学 土木工程与建筑学院， 湖北 武汉 430070)

近年来，城市建设规模和速度的不断加快导致了城市被拆迁房屋数量的急剧上升，拆迁纠纷日益加剧，城市被拆迁房屋的市场价格是确定拆迁补偿金额的根本依据，客观公正的评估其市场价格是一项责任重大的社会工作。根据2003年建设部颁布的《城市房屋拆迁估价指导意见》中相关规定，拆迁估价可选用市场比较法，成本法，收益法等，它们在实际运用过程中均存在不同程度的局限性，主要表现为估价过程的主观随意性较大，作业效率低等。因此，本文将BP神经网络理论引入城市拆迁房屋估价领域，充分发挥其非线性动态自适应系统处理问题的能力，旨在减少估价作业的主观随意性和提高作业效率，为进一步改进和完善城市房屋拆迁估价作业方法提供思路。

1 基于BP网络的拆迁估价流程设计

人工神经网络(ANNs)是一种通过模拟生物神经系统的行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，利用神经元之间的相互联系与制约，实现输入到输出的非线性映射。被拆迁房屋的房地产市场价格受到多重因素的综合作用，各种因素的作用程度、影响方式、因素之间存在的制约关系等都难以用精确的数学语言描述，神经网络能够在处理大量无法用数学规则或公式描述的并行式信息时表现出极大的自适应性和灵活性，将其引入城市房屋拆迁估价领域，可以不用事先假设各影响因素之间符合的规律、数据服从的分布情况以及提供精准的数学模型，只需通过搜集一定数量可靠的已知样本，调查获得样本输入/输出信息，建立评估指标体系、设计BP网络结构与选择合适的算法，构建网络估价模型，应用已知样本的输入/输出信息对模型进行训练，模型一旦训练成功并检测合格，即可用于预测被拆迁房屋的市场价格。图1描绘了基于BP网络的房屋拆迁估价流程，其中网络模型的构建是估价作业的核心步骤，成功构建网络模型是实现模型预测功能的重要前提与基础。

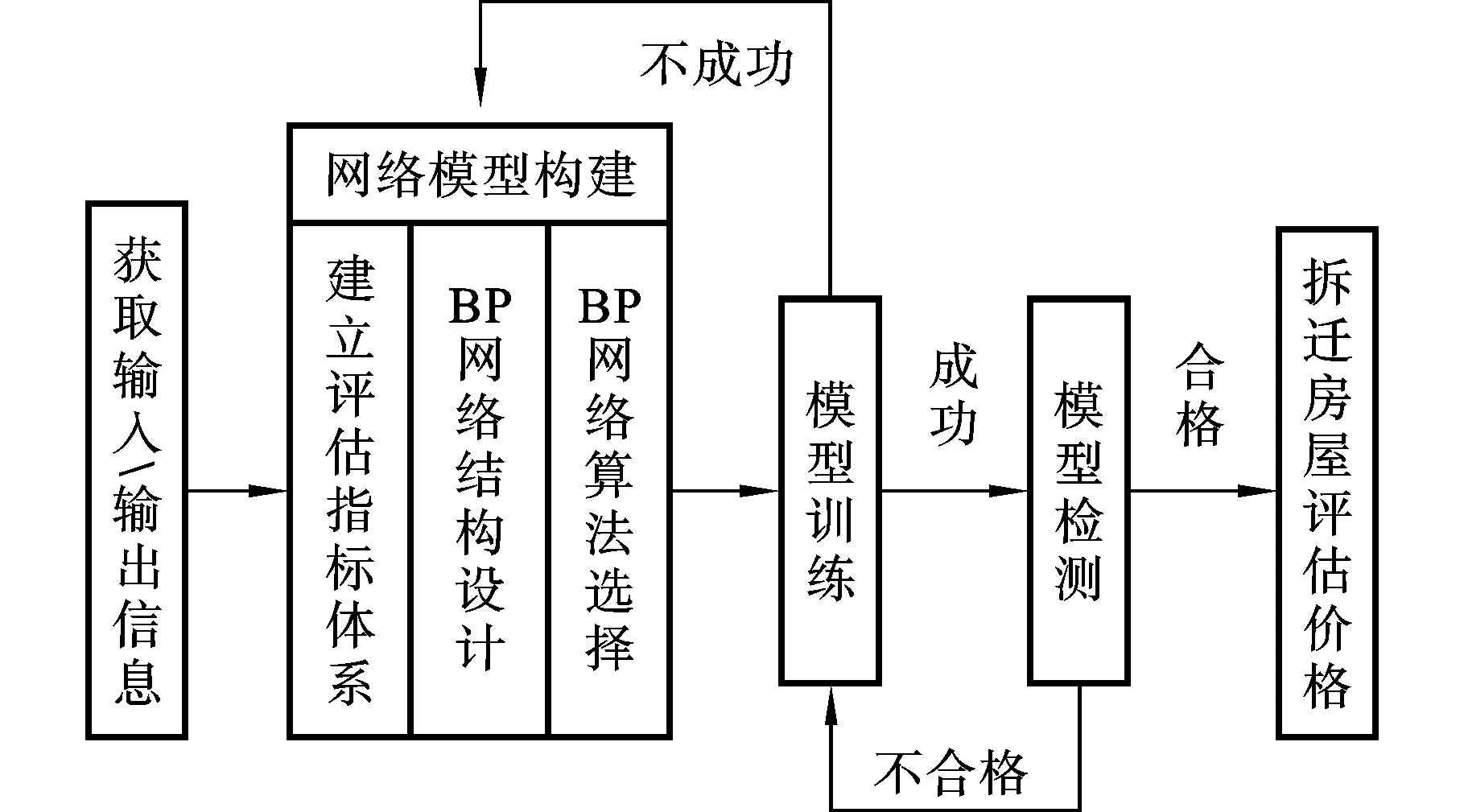
图1 基于神经网络的被拆迁房屋估价流程

2 基于BP网络估价模型的构建

2.1 估价指标体系构建及量化标准

住宅是城市房屋拆迁中比较普遍的拆迁对象，住宅拆迁与城市居民的切身利益息息相关，也是最易引发纠纷的拆迁类型。本文以住宅拆迁估价为研究对象，构建住宅类被拆迁房屋的价格评估指标体系。一般地，影响城市被拆迁房屋市场价格的因素按照作用范围的不同可以分为一般因素、区域因素和个别因素共三类。在一定的时间内，政治环境、经济发展处于相对稳定状态，对个体价格差异的作用微弱，而区域因素和个别因素是造成被拆迁房屋价格差异的主要因素。另外，由于神经网络的输入向量维数过多会影响样本训练时的收敛速度和收敛效果，指标数量并非越多越好，选取对被拆迁房屋价格有显著作用的因素，剔除微小因子影响。因此，在宏观环境稳定的情况下，重点对区域因素和个别因素的作用效果进行分析，参考《武汉市房屋重置价格标准》及《城市房屋拆迁估价指导意见》中关于房屋分类标准、结构类型和房屋成新率的有关规定等，建立如表1、表2所示的评价指标体系，其中区域因素与个别因素的指标量化方法采用10分制评分法，将其指标划分为优(9～10分)、较优(7～8分)、中(5～6分)、较劣(3～4分)、劣(1～2分)5个等级。

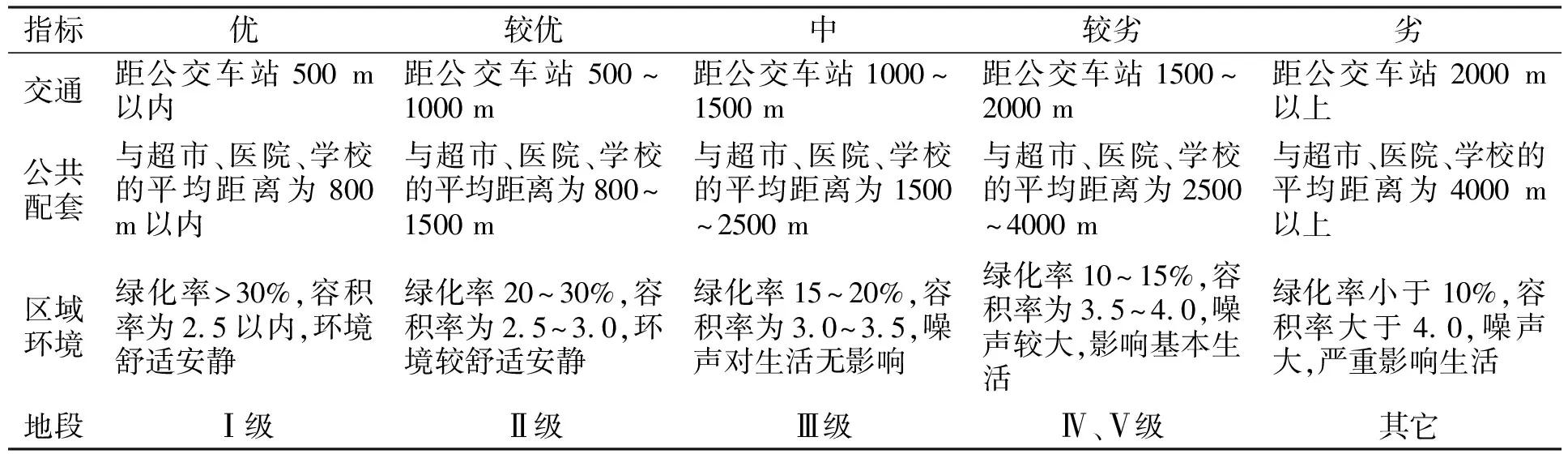
表1 区域因素评价指标及量化标准

表2 个别因素评价指标及量化标准

鉴于待估对象为城市被拆迁房屋，案例搜集的范围以二手房市场的交易实例为主。与市场法类似，BP神经网络的估价是基于已知样本即房地产市场的交易实例，因此在搜集案例过程中，不仅需考虑区域因素与个别因素对市场价格的作用，同时应分析交易时点及交易状况对房屋最终成交价格的影响。表3描述了基于BP网络的交易时点及交易情况的量化标准，量化后的指标值(以中国指数研究院二手房研究中心定期发布的二手房价格指数月报为量化值)作为网络的输入信息，通过神经元间的连接与信息传递，影响最终的市场价格。

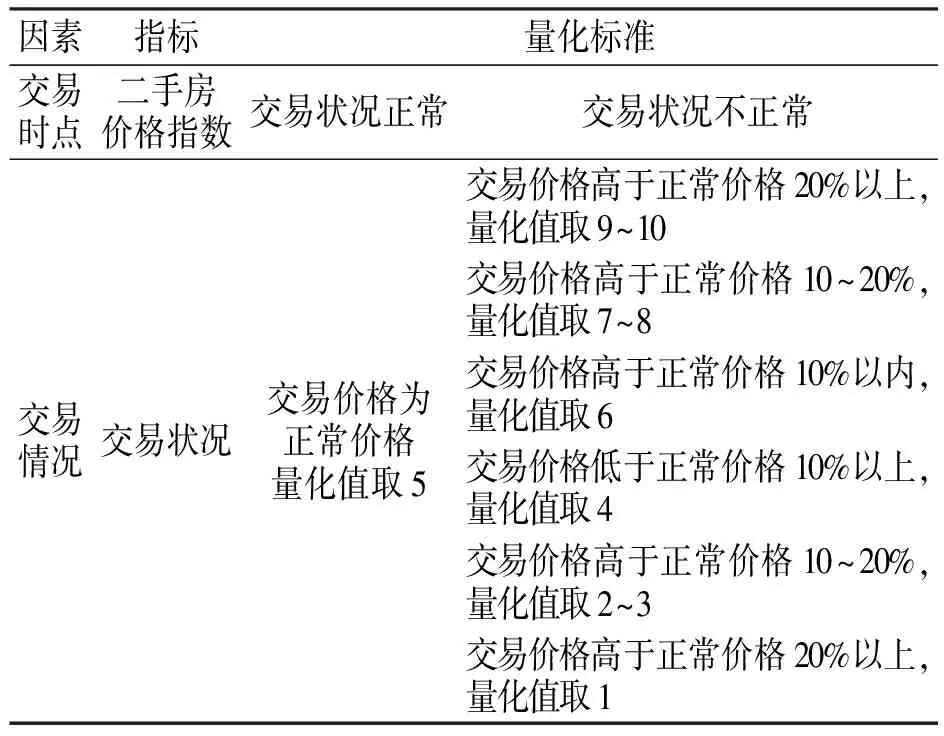
表3 交易日期与交易情况指标及量化标准

2.2 BP网络结构设计

BP神经网络是目前应用最为广泛的一种按误差逆传播算法训练的多层前馈网络，由输入节点、单个或多个隐含层及输出层构成。BP网络结构设计包括确定网络层数、输入节点数、输出层及隐含层神经元个数等。理论证明具有偏差和至少一个S型函数的隐含层可以逼近任何有理函数，为避免结构复杂化导致的收敛缓慢或训练失败，城市房屋拆迁估价模型应采用单隐层网络结构，隐含层传递函数为非线性函数tansig，输出层则采用纯线性函数purelin，前述的12个评价指标量化值作为网络的输入节点，输出神经元为房屋的市场价格，输入/输出是多对一的映射关系。BP网络训练结果的好坏与隐含层神经元的个数息息相关，一般采用实验法确定。基于后文应用研究的对象，图2构建了适用于武重宿舍房屋拆迁估价模型的单隐层网络结构，其中向量p为输入数据即量化指标值，y为房屋的市场预测价格。经过反复实验，当隐层节点数为13时，估价模型的训练达到满意效果。

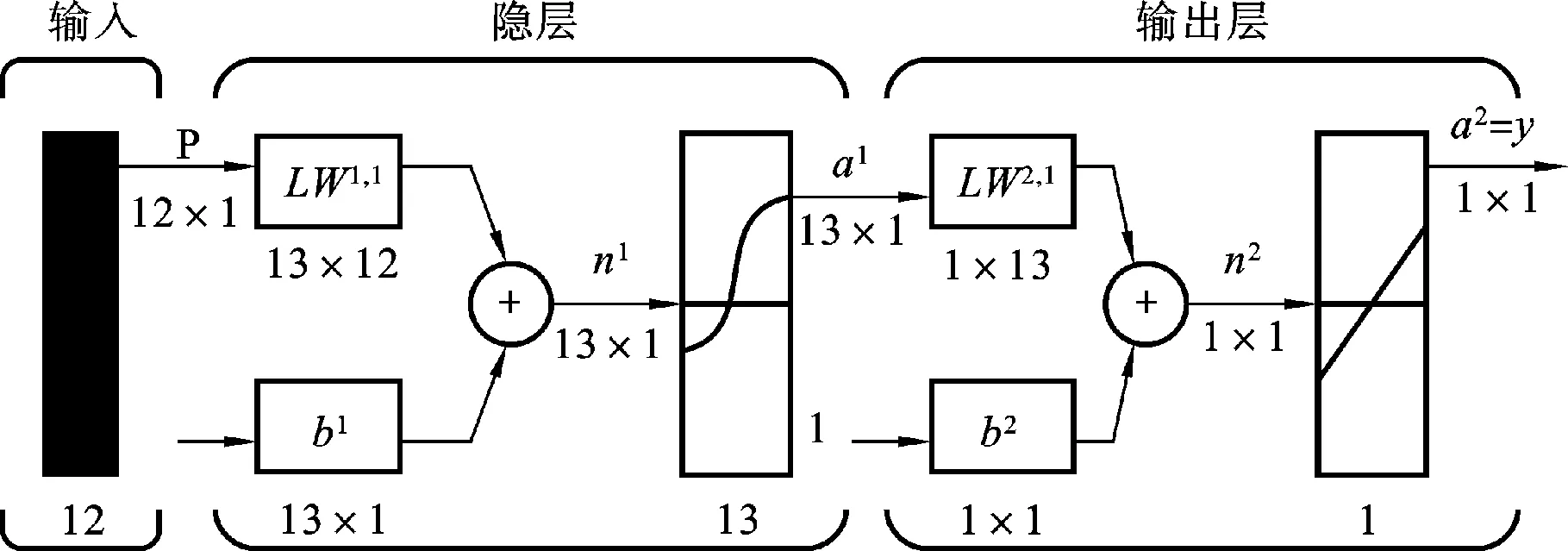
图2 估价模型的单隐层网络结构

2.3 BP网络学习算法的选择

BP学习算法分为输入的正向传递和误差的反向传播两个阶段，被拆迁房屋的输入数据经隐含层和输出层神经元处理后得到房屋市场价格，以此作为网络输出结果，当该值与期望输出即房屋的实际交易价格之间的差值不满足误差范围时，误差信号将沿输出层逆向传播，据此调整各层神经元的连接权值和阈值，经过反复迭代使误差达到允许值，网络学习过程结束，训练成功。房屋拆迁估价属于中小型规模矩阵的函数逼近问题，选用L-M优化算法对网络权值进行修正能够达到学习速率最快，收敛最迅速的效果，其算法实现的原理如下：

(1) 信号的正向传递：

隐含层第i个神经元的输出为：

输出层第k个神经元的输出为：

(2) 误差的反向传播：

误差函数定义为：

隐层与输出层权值修正公式：

wij(t+1)=wij(t)-(JTJ+uI)-1JTe

式中，wij(t+1)表示网络经第t+1次迭代后的网络权值，wij(t)为第t次迭代时的网络权值，J表示误差对权值微分的Jacobian矩阵。JTe计算其梯度，e为误差向量。μ进行自适应调整，当u→∞时，算法变为梯度下降法；当u→0时，算法变为近似Hessian矩阵的牛顿法。 L-M算法的实质是尽可能的使其运算具有接近于牛顿法的收敛速度。

3 应用研究

本文以武汉市武昌区进行拆迁的武重宿舍为对象进行实证研究，选取该小区中的一个标准的待估对象作为预测样本，通过查阅政府有关部门公布的房地产价格资料，报刊、网络资源、向房地产经纪人了解房地产成交价格及情况等，在二手房交易市场共搜集了10宗与待估被拆迁房屋同类型的交易案例，作为网络的已知样本，通过实地跑盘调查，记录已知样本的基本情况，根据上述标准进行专家量化打分，将其转化为网络的输入/输出数据，运用Matlab函数工具箱编程语言实现前述构建的BP网络模型的训练、仿真和预测功能。

3.1 估价模型的训练

网络训练选取Levenberg-Marquardt 优化算法以提高网络的泛化能力和收敛速度，其中最大训练步数设定为500，目标误差值设定为0.01，显示频数为30。在所搜集的10个已知样本中，随机选取7个样本作为网络的训练样本，表4详细记录了训练样本指标量化后的已知输入和期望输出数据，以及网络经过学习训练后的计算值。期望输出与网络计算值之间的误差满足1%的目标误差要求，网络训练达到满意效果。

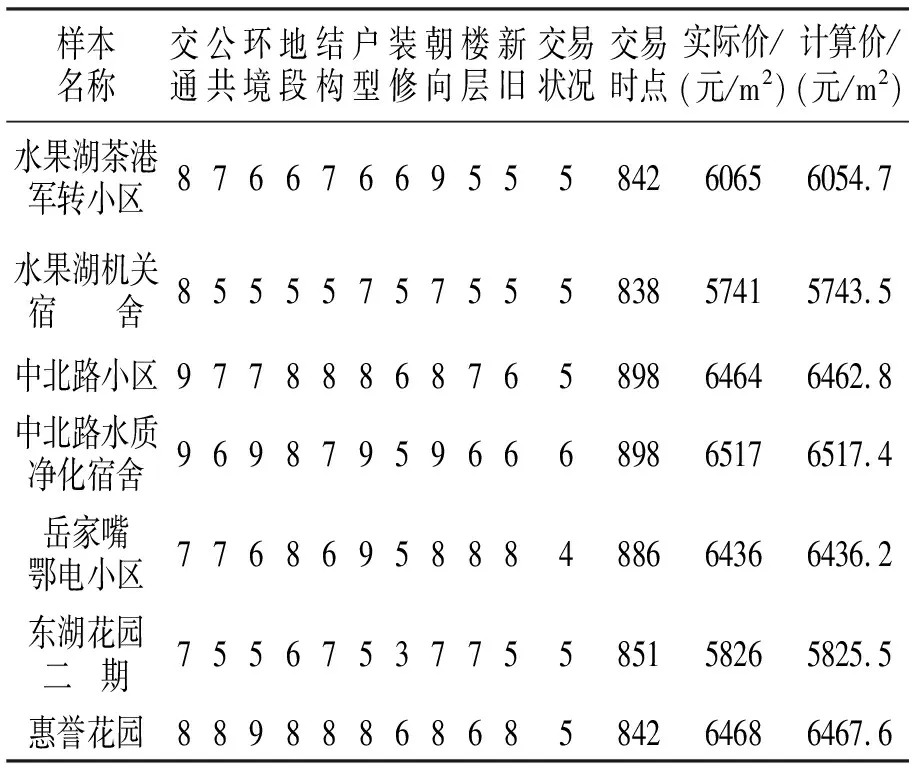
表4 训练样本输入与输出数据

图3表示BP网络经过2个循环训练后，训练样本的期望输出与计算输出的误差小于1%，即网络达到预定的目标误差，训练成功。

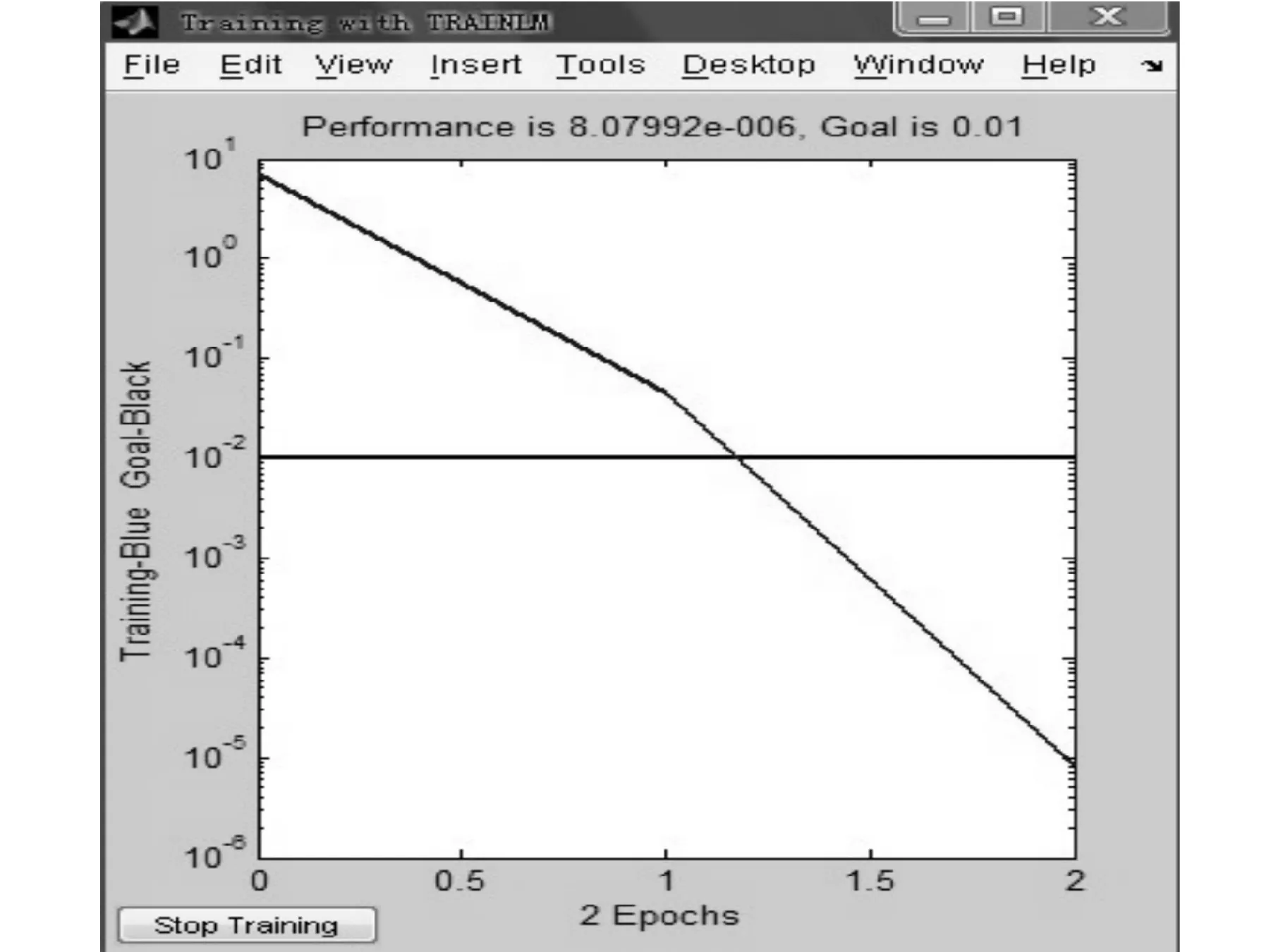
图3 网络训练结果

下图反映了训练样本实际值与网络计算值的线性回归分析，从图中可知实际值与计算值之间实现了合理准确的线性拟合。

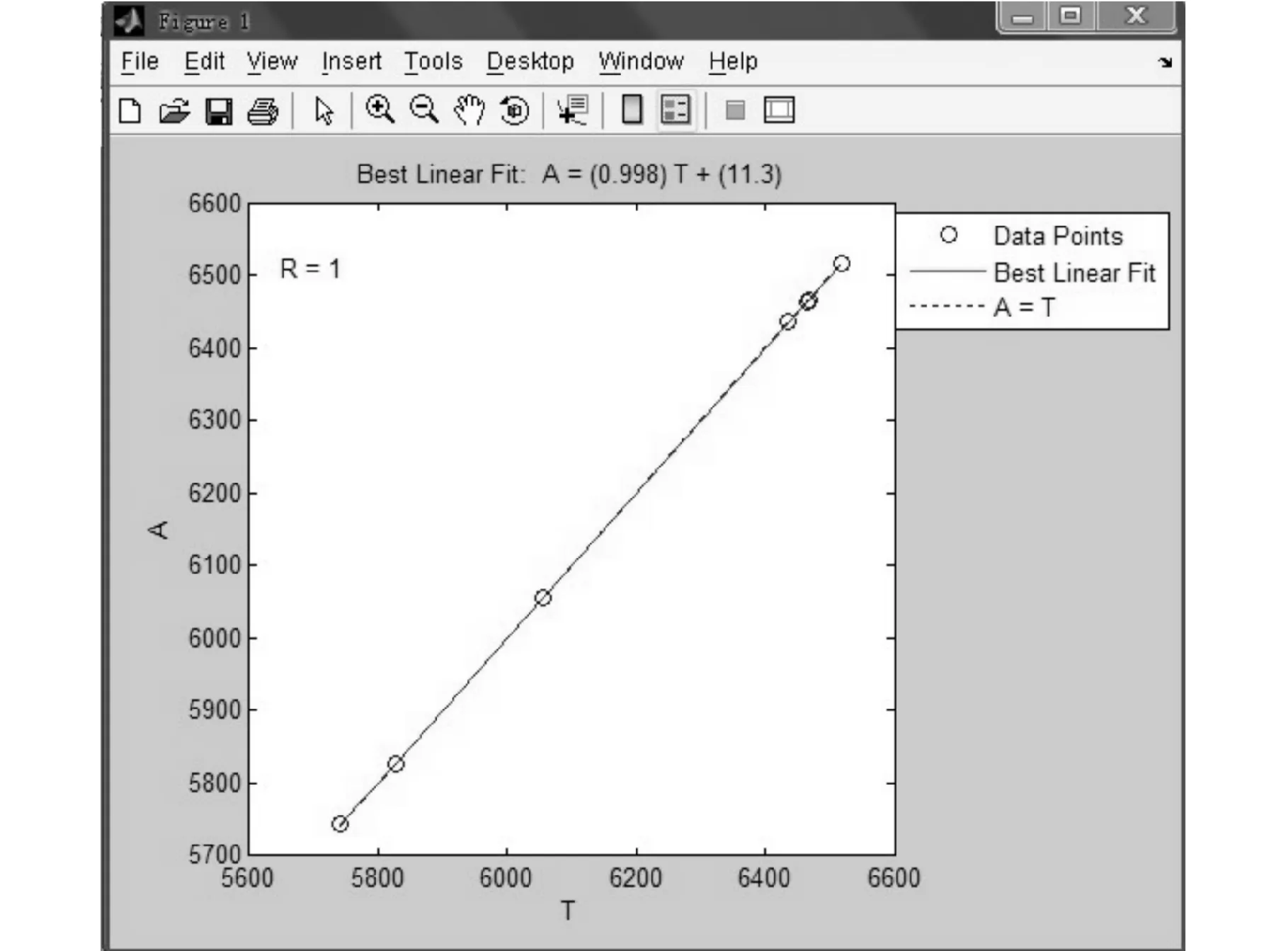
图4 回归分析

3.2 估价模型的检测与预测

网络训练成功后，需要对网络进行检测，用于检测的已知样本称为检测样本，当检测样本的计算值与期望输出值之间的差值达到预先设定的目标误差时，网络检测合格。检测合格的网络才可用于预测，否则应重新对网络进行训练。表5反映了3个检测样本的已知输入/输出数据及网络的计算值，相对误差达到1%以内，检测合格，运用该网络估价模型对待估的被拆迁房屋进行市场价格预测，估价结果如表6所示。

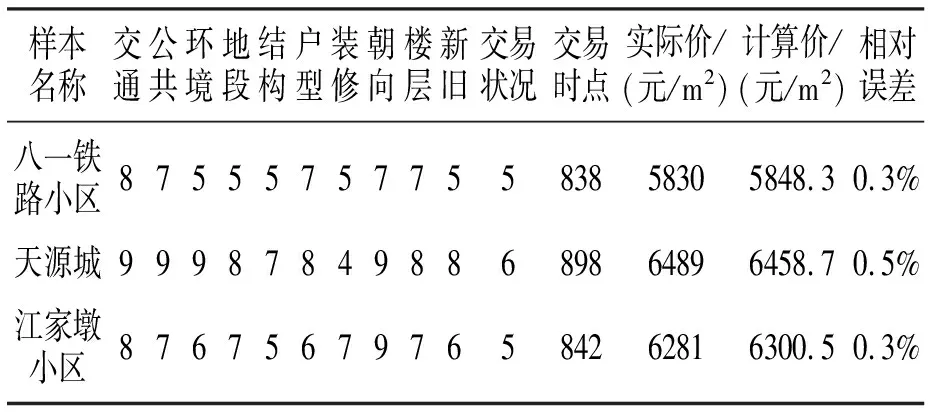
表5 检测样本输入与输出数据

表6 待估对象输入与估价结果

4 结 语

本文基于BP神经网络探讨了城市被拆迁房屋市场价格评估的方法，通过设计评估流程和构建评估模型，运用实证数据对网络进行训练、检测和预测，使模型计算输出与期望输出保持在1%的误差范围内，与传统方法相比，该方法具有以下特点：

(1)一定程度上避免了市场法等确定修正系数的主观性。神经网络能够运用自学习和自适应能力较为客观公正的揭示已知样本影响因素与价格之间的非线性关系，缓解估价作业过程的主观因素作用，提高估价结果的公信力。

(2) 与计算机技术相结合，提高了估价作业效率。通过调用Matlab函数工具箱能够快速构建BP网络，实现其功能，避免复杂低效的手工计算。另外，网络模型一旦训练成功，即可用于评估同类型成百上千的被拆迁房屋的市场价格，避免了拆迁估价作业一次性特点，减少了大量重复性工作，克服了拆迁估价作业量大，时间紧迫的问题，为拆迁估价作业方法提供新的思路。

[1]任 宏, 夏 刚. 土木工程学报[J]. 基于实物期权的房屋拆迁补偿估价研究, 2008, 5(5): 75-76.

[2]张晓平, 周芳芳, 谢 朝. 基于神经网络的房地产估价模型研究及其Matlab 实现[J].技术经济与管理研究, 2009, (2): 23-25.

[3]杨黎萌, 刘开第. BP神经网络在房地产估价中的应用[J]. 河北建筑科学学院学报, 2004, 21: 106-109.

[4]Floyd C F, Allen M T. Real Estate Principles[M]. Chicago：Dearborn Real Estate Education, 2002.

[5]闻 新, 周 露. MATLAB神经网络应用设计[M]. 北京:科学出版社,2000.

[6]李 刚. 基于人工神经网络的房地产估价研究[D]. 西安: 长安大学, 2006.

[7]Howard B Demuth, Mark H Beale. Neural Net Work Toolbox User′s Guide[M].The Math Works，2000.

[8]陈小前, 罗世彬, 王振国，等. BP神经网络应用中的前后处理过程研究[J] .系统工程理论与实践,2002,1(1):65-70.

[9]柴 强. 房地产估价[M]. 北京, 首都经济贸易大学出版社, 2005.

[10]杨宝华. 基于Matlab的BP神经网络应用[J]. 电脑 知识与技术， 2008，(4)：124-125.

[11]Dennis S Tosh, William B Rayburn. Fundamentals of Real Estate Appraisal [M].Dearborn Financial Publishing，2001.