具有极小 Hosoya指数的含圈共轭图

孙志荣

(安徽大学数学科学学院,安徽合肥230039)

0 引 言

图G(V(G),E(G))为n阶一般无向共轭图,即图 G含有完备匹配.其顶点集为V(G),边集为 E(G).图G的匹配是指G中的边子集N,在N中任意两条不相同的边均无公共点.m(G,k)表示G中恰含k条边的匹配个数并且规定m(G,0)=1.图的 Hosoya指数 (或简称 z-指数)指的是图 G的所有匹配之和,记为z(G),即z(G)=(G,k),显然,当 时,m(G,k)=0.Hosoya指数是由Hosoya于1971年提出来的,作为组合数学中的一个重要的拓扑指标,它与分子的总π-电子能[1]、沸点[2]等化学物理特性有密切关系.

近年来,国内外已有很多关于 Hosoya指数的研究成果.例如在 n个顶点的树中,路 Pn和星图Sn分别具有最大和最小的Hosoya指数[3,4].固定圈长单圈图且具有最小Hosoya指数的极值图[5]和给定悬挂点个数的单圈图集合中具有最小 Hosoya指数的极值图[6]已被刻画出.欧建平刻画了单圈图的最大、次大的Hosoya指数及其极值图[7]和没有完备匹配的树当中 Hosoya指数最大的极值图[8].n阶树中具有 m-匹配的第三小 Hosoya指数是 2m-4(10n-15m+11)[9].n个顶点的树中具有 m-匹配的第四小、第五小的Hosoya指数分别为2m-4(12n-18m+4)和2m-4(12n-18m+5)[10].n个顶点的双圈图中具有最大Hosoya指数的图由4阶圈和n-2阶圈共用一条边得到[11],具有最小 Hosoya指数的图由含一条公共边的两个三角形并在公共边的一个顶点加 n-4个悬挂点得到[12].含 n个点的无圈图的第二小 Hosoya指数为2n-3[13].一些给定特殊条件的图类的 Hosoya指数也被刻画出,例如直径是3和4的 n阶树的 Hosoya指数的最大值[14]和双星树的Merrifield-Simmons和 Hosoya指数序列[15]等.对于无圈图和单圈图,积和式和Hosoya指数有着一定的联系,利用积和式可以求出一些特殊单圈图的极小 Hosoya指数[16].此外,Hosoya指数与图的能量[17]和常见的六角链化学分子的某些特性[18]也有联系.但是对于共轭分子图的Hosoya指数的研究并不是很多,本文则刻画了共轭分子的含圈图中具有最小、次小 Hosoya指数的极值图.

1 定义与符号

下面先介绍一些定义,其它未加说明的图论术语和符号请参考文献[2].G有完备匹配,因此|V(G)|=n为偶数,|E(G)|=m(n≤m≤-2).dG(u)表示顶点 u在图G中的度.φn,m表示含有n(n≥8)个顶点 m(n≤m≤-2)条边的共轭图集合.M(G)表示图G的完备匹配,则|M(G)|=Q(G)=E(G)-M(G)表示G去掉M(G)中的边剩下的边集合.用 G＊表示图 G去掉完备匹配的边集,再去掉孤立点剩下的子图,即由边集Q(G)导出的子图,因此|E(G)＊|=m-对于图 G的任何一个k-匹配Ω,都可以分成两部分Ω=R∪S,其中 R∈E(G＊),S∈M(G),即 G的任一k-匹配,都可以从 G＊中选择 i(0≤i≤k)条不相邻的边,再从 M(G)中选择 k-i条边,且保证 M(G)中的 k-i条边和G＊中的i条边互不相邻.

2 引 理

引理1 a,b为正整数,若 a+b=n,则 ab≥n-1.

证明 a+b=n,所以a=n-b.

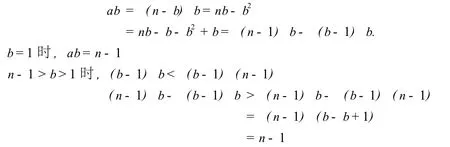
即ab＞n-1.

综上所诉,ab≥n-1.证毕

引理3 若 (X,Y)是一个二部图 G的二部划分,|E(G)|=p,且满足|X|≥2,|Y|≥2.则这个二部图至少有 p-2个2-匹配.

证明 G是二部图,所以 G没有奇圈.

如果二部图 G可以分成边不交的两部分G1和 G2,即 G是不连通的,设|E(G1)|=a,|E(G2)|=b,则 a+b=p.按照从 G1中选择一条边,从 G2中选择一条边的方法组成 2-匹配.根据引理1,则至少可以选出 ab≥p-1个2-匹配.

若G是连通的,即不能分成边不交的两部分,且二部划分|X|≥2,|Y|≥2,则在 G中存在边uν,满足 d(u) ≥2,d(ν) ≥2.设 d(u) =k1,d(ν)=k2.由于 G不含奇圈,除了边 uν之外,与 u关联的k1-1条边和与ν关联的k2-1条边无公共顶点.设与u关联的边集为E1,与ν关联的边集为E2,则|E1-uν|=k1-1,|E2-uν|=k2-1.首先边 uν可与 p-1- (k1-1) - (k2-1)条边组成 p+1-k1-k2个 2-匹配.按照从 E1-uν和 E2-uν中各取一边的选法至少有 (k1-1)(k2-1) ≥k1+k2-3个2-匹配,所以图 G至少有p+1-k1-k2+k1+k2-3=p-2个2-匹配. 证毕

3 结 论

定理4 若 G∈φn,m(n≤m≤n+n-2),G≠Hn,m,则 z(G)＞z(Hn,m). Hn,m如图1所示,由-i-2 1个三角形和一条悬挂边及i个 P2的端点粘合在同一点组成.

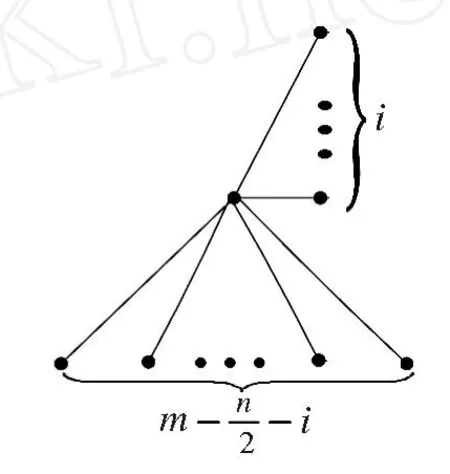
图2

图1 Hn,m

证明 如果对任意 G∈φn,m和都满足 m(Hn,m,k)≤m(G,k),那么,就可以证明(H,k) ≤ m(G,k),即z(H) ≤z(G).n,mn,m

定理5 若 G∈φn,m(n≤m≤n+-3),G≠Hn,m,In,m,则 z (G) ＞z (In,m). In,m是在 Hn-1,m-2的一个三角形的两个2度顶点上各加一个悬挂点得到,如图3所示.

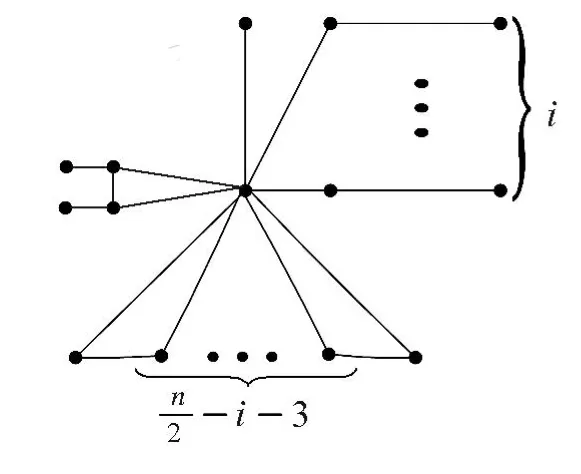
图3 In,m

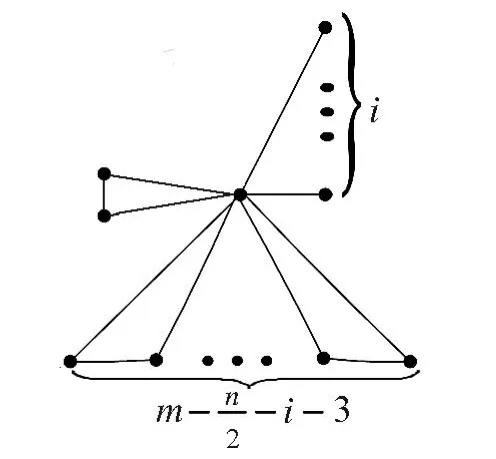
图4

证明 In,m如图3所示,如图4所示.先考虑In,m的Hosoya指数,z(In,m)= m(In,m, k).中有m个1-匹配,有 m--3个2-匹配,没有3-匹配,且中的每个i-匹配(i=0,1,2)与M (In,m)中的2i条边相邻.即:

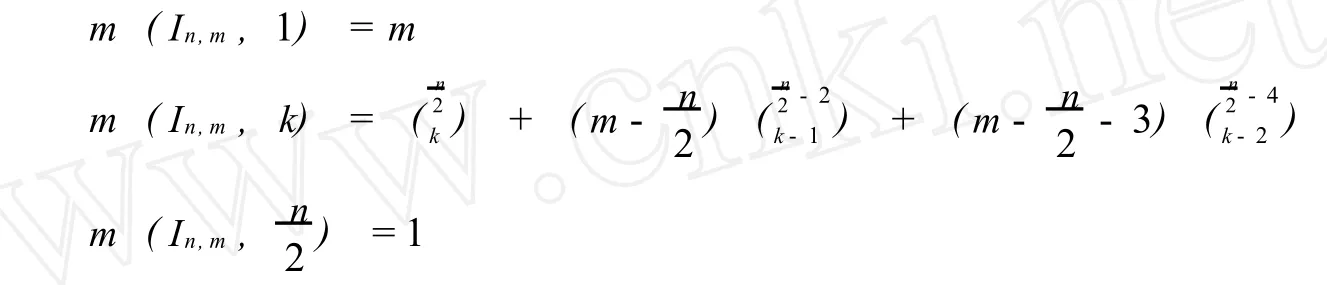
G∈φn,m,G≠Hn,m,In,m,把 G分两种情况讨论:

情况1 若 G＊是非连通图,则 G＊至少包含两部分边非空的子图 G1和 G2.设|E(G1)|=a,|E(G2)|=b,则a+b=.假设 a≥b,由引理1可知 ab≥-1,若从 G1中选一条边,从 G2中选一条边,则至少可构成2-匹配至少m-n-1个,且每个2-匹配至多关联4条 M(G)中的边.所以:

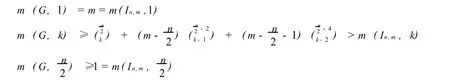
情况2 若 G＊是连通图,G≠Hn,m,In,m,则 G＊是非星图,且|V (G＊) |≥4,则在 G＊中存在割边集B把G＊分割成边非空的两个子图 G1和 G2,即 EG＊(G1,G2)=B.由割边集B生成的子图可视为一个二部分图,设|B|=p. |E(G1)|=a,|E(G2)|=b,则a+b=-p.首先按照从 G1中选择一条边,从 G2中选择一条边的方法至少可组成ab≥p-1个2-匹配.

子情况2.1 若割边集B只含一条边,即 p=1,则 G＊至少可组成 ab≥-2个2-匹配.

子情况2.2 若由割边集B生成的子图是星图,则 G1和 G2中至少有一边可与星图的 p-2条边组成p-2个2-匹配.G＊至少含-3个2-匹配.

子情况2.3 若边集B生成的子图不是星图,由引理3可知割边集B本身至少含p-2个2-匹配,则G＊至少含-p-1+p-2=-3个2-匹配.

在以上三种情况中,由于每个2-匹配最多与M(G)中的4条边相邻,则

[1] Hosoya H.Topological index,a newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons[J].Bull Chem Soc Jpn,1971,44(09)：2332-2339

[2] Gutman I,Polansky OE.Mathematical Concepts in Organic Chemistry[M].Berlin：Springer,1986：1-70

[3] Chan O,Gutman I,Lam TK,et al.Algebraic connections between topological indices[J].J Chem Inform Comp Sci,1998,38(01)：62-65

[4] Gutman I.Acyclic systems with extremal Huckelπ-electron energy[J].Theor Chim Acta,1977：78-87

[5] Qu JP.On extremal unicyclic molecular graphs with prescribed girth and minimal Hosoya index[J].J Math Chem,2007,42(03)：423-432

[6] Hua HB.Hosoya index of unicyclic graphs with prescribed pendent vertices[J].J Math Chem,2008,43(02)：831-844

[7] Qu JP.On extremal unicyclic molecular graphs with maximal Hosoya index[J].Discr Appl Math,2009,157(02)：391-397

[8] Qu JP.Maximal Hosoya index and extremal acyclic molecular graphs without perfect matching[J].Appl Math Lett,2006,19(07)：652-656

[9] Ye C,Wang JF,Zhao H.Trees with m-matchings and the third minimal Hosoya index[J].Comm Math Comp Chem/MATCH,2006,56(03)：593-604

[10] Ye CF,Wang JF.Trees with m-matchings and the fourth and fifth minimal Hosoya index[J].Comp Math Appl,2008,56(02)：387-399

[11] Deng HY.The largest Hosoya index of(n,n+1)-graphs[J].Comp Math Appl,2008,56(10)：2499-2506

[12] Deng HY.The smallest Hosoya index in(n,n+1)-graphs[J].J Math Chem,2008,43(01)：119-133

[13] Hou YP.On acyclic systems with minimal Hosoya index[J].Discr Appl Math,2002,119(03)：251-257

[14] 曹庆信,陈祥恩,刘信生.直径是3和4的n阶树的Hosoya指数的最大值[J].甘肃联合大学学报,2009,23(03)：31-34

[15] 肖正明.双星树的Merrifield-Simmons和 Hosoya指数序列 [J].湖南城市学院学报,2007,16(04)：50-52

[16] Hua HB.Minimizing a class of unicyclic graphs by means of Hosoya index[J].Math Comp Modell,2008,48(5-6)：940-948

[17] Heuberger C,Wagner SG.Chemical trees minimizing energy and Hosoya index[J].J Math Chem,2009,46(01)：214-230

[18] Shiu WC.Extremal Hosoya index and merrifield Simmons index of hexagonal spiders[J].Discr Appl Math,2008,156(15)：2978-2985