关于不定方程x2+(p-1)y2=pz2

管训贵

(泰州师范高等专科学校数理系,江苏泰州225300)

1 引言及主要结论

对于不定方程

文[1]给出了 p=3时的一切正整数解.本文将给出任一奇素数 p≡3(mod4)时的通解公式,从而推广了文 [1]中的结论.

首先注意到,如果 (x,y) =p,由 (1),p2|pz2,即 p|z2.因为 p为奇素数,所以 p|z,这样就可在 (1)式两边约去 p.如果 (x,y) =d,(d,p) =1,由 (1),d2|z2,故 d/Z,同样可在 (1)式两边约去 d,所以在讨论 (1)的正整数解时,可设 (x,y) =1[2-4].此外,本文最关键是解决当 p-1无平方因子时 (1)的求解问题.对于 (1)的正整数解,经过以上简化之后,有如下

定理 设 p为奇素数,且 p-1无平方因子,当 p≡3(mod4)时,不定方程 (1)满足 (x,y)=1的一切正整数解可表示为

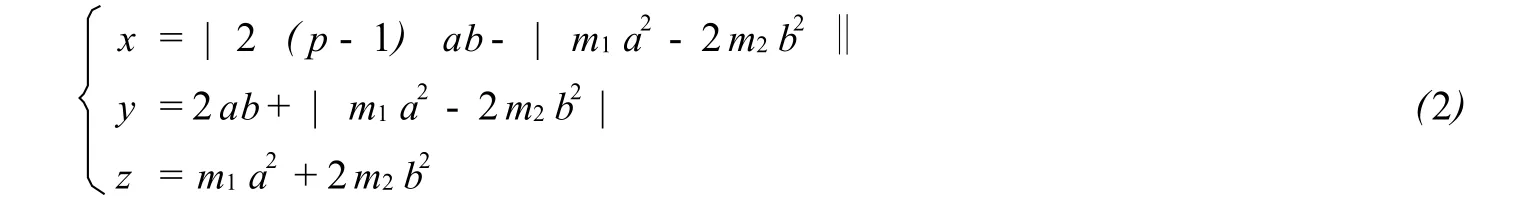
这里 a,b,m1,m2均为正整数,且 (a,b) = (b,m1) = (a,2m2) =1,p=2m1m2+1.

2 关键性引理

引理 设 p为奇素数,且 p-1无平方因子,当 p=4k-1(k为正整数)时,不定方程

这里 a,b,m1,m2均为正整数,且 (a,b) = (b,m1) = (a,2m2) =1,p=2m1m2+1.

证明 对于 (4)中所给出的正整数 u,v,w,显然有

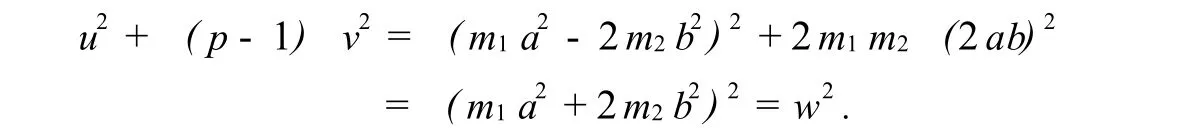
假定 (u,v) ≠1,即存在素数q,使得q|x,q|y,则由 u2+ (p-1)v2=w2知,q|w,因此可得q|(w+u)且q|(w-u),即q|2m1a2且q|4m2b2,于是q|2(m1a2,2m2b2).

又由 (a,b) = (b,m1) = (a,2m2) =1知, (m1a2,2m2b2) = (m1,2m2),故 q|2 (m1,2m2).而 p-1=2m1m2无平方因子,即 (m1,2m2) =1,所以q|2,从而q=2.由此推出2|u.

此外,2m1m2=2(2k-1),(a,2m2) =1,说明m1,m2与 a皆为奇数,故 u=|m1a2-2m2b2|为奇数,即2łu.这与前面的结果矛盾.因此 (u,v)=1.就是说由表达式 (4)所给出的 u,v,w都是(3)的正整数解.

反之,设u,v,w是 (3)的满足 (u,v) =1的任一正整数解,则

考虑到2k-1无平方因子,所以必存在正整数 a,b,m1,m2,满足

考虑到2k-1无平方因子,所以必存在正整数 a,b,m1,m2,满足

就是说,(3)的任一正整数解都能由表达式 (4)给出.

3 定理证明

容易验证 (2)是方程 (1)的满足条件的正整数解.

反之,设 x,y,z是方程 (1)的正整数解,若 p|y,则 p|x,这与 (x,y) =1矛盾,故必有 p ły.方程 (1)可化为

代入方程 (1)得

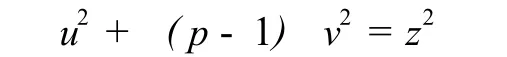
且由 (x,y) =1知,(u,v) =1.

再根据引理及 (7)式可得方程 (1)满足条件的正整数解为 (2).

若p|(x-y),因x+(p-1)y= (x-y) +py,必有p|[x+ (p-1)y].

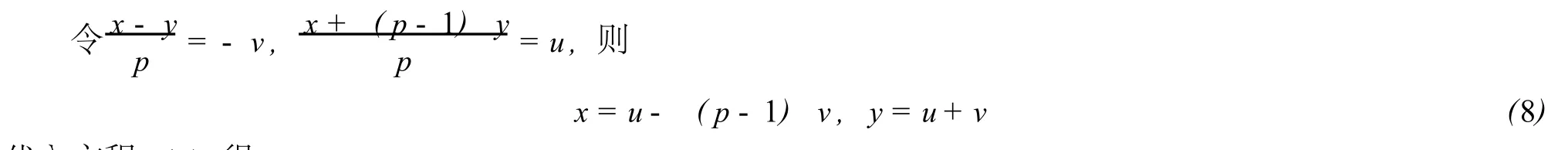
代入方程 (1)得

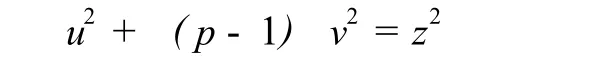
且由 (x,y) =1知,(u,v) =1.

再根据引理及 (8)式可得方程 (1)满足条件的正整数解为 (2).

定理得证.

[1] 汤健儿.不定方程 x3+y3=z2与 x3+y3=z4[J].数学的实践与认识,1993,(01)：90-94

[2] 柯召,孙琦.谈谈不定方程 [M].上海：上海教育出版社,1980：38-40

[3] 潘承洞,潘承彪.初等数论 [M].北京：北京大学出版社,1992：95

[4] 闵嗣鹤,严士健.初等数论 [M].北京：高等教育出版社,2004：35

[5] 管训贵.关于不定方程z2+2(2xy)2=(x2-y2+2xy)2[J].河北北方学院学报：自然科学版,2009,25(01)：14-15

[6] 管训贵.不定方程 x2-py2=z2的正整数解 [J].河北北方学院学报：自然科学版,2009,25(05)：5-7