用MA TLAB解决规划问题的通用方法

赵喜清,刘守义,韩振芳

(1.河北北方学院信息科学与工程学院,河北张家口075000;2.河北北方学院学报编辑部,河北张家口075000;3.河北北方学院理学院,河北张家口075000)

利用Excel提供的规划求解法可以解运筹学中的许多问题,方法简捷、精度较高[1],但对于有无穷多最优解的问题,该方法只能给出其中的一个解.另外,Excel规划求解将使用“在插入”试用值的迭代数值的方法,涉及可变单元格和观察由约束单元并获得最佳的单元格计算结果.每次试验称为一个“迭代”,Microsoft Excel规划求解将执行广泛的观察所得的输出的分析和输入,这样的纯“试验和错误”方法将需要一个非常长的时间[2](尤其对于问题涉及许多可变单元格和约束).

1 EXCEL规划求解的过程

EXCEL规划求解步骤：

1)加载“规划求解”宏、引用“规划求解”工具.

2)设置“规划求解参数”.

将“设置目标单元格”指向设定目标利润值的单元格;将“可变单元格”即指向所设定的“产量值”(未知数)的单元格;将上述的资源约束条件,用 EXCEL语言引入“约束”;设置规划求解“选项”参数,根据实际情况,选择“采用线性模型”和“假定非负”两个选择项.

3)求解参数设定后,由EXCEL自动求解,得出最终结果.

以“合理配餐问题”为例,说明 EXCEL规划求解的过程.

合理配餐问题是非常复杂的问题,涉及的因素很多,如一公司饲养实验用的动物以供出售,已知这些动物的生长对饲料中的三种营养成分蛋白质,矿物质,维生素特别敏感,每个动物每天至少需要蛋白质70 g,矿物质3 g,维生素10 mg,该公司能买到五种不同的饲料,每种饲料1 kg所含的营养成分及每种饲料成本如表1所示：

在分析了约束条件后,确定目标函数,建立数学模型,以下为EXCEL求解过程 (见图2)：

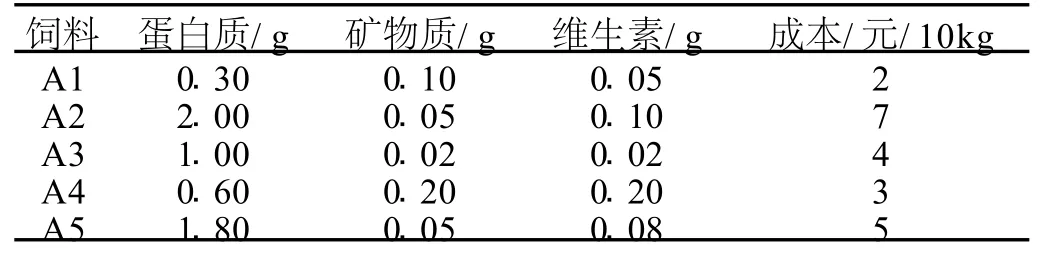
表1 一公司饲养动物营养成分

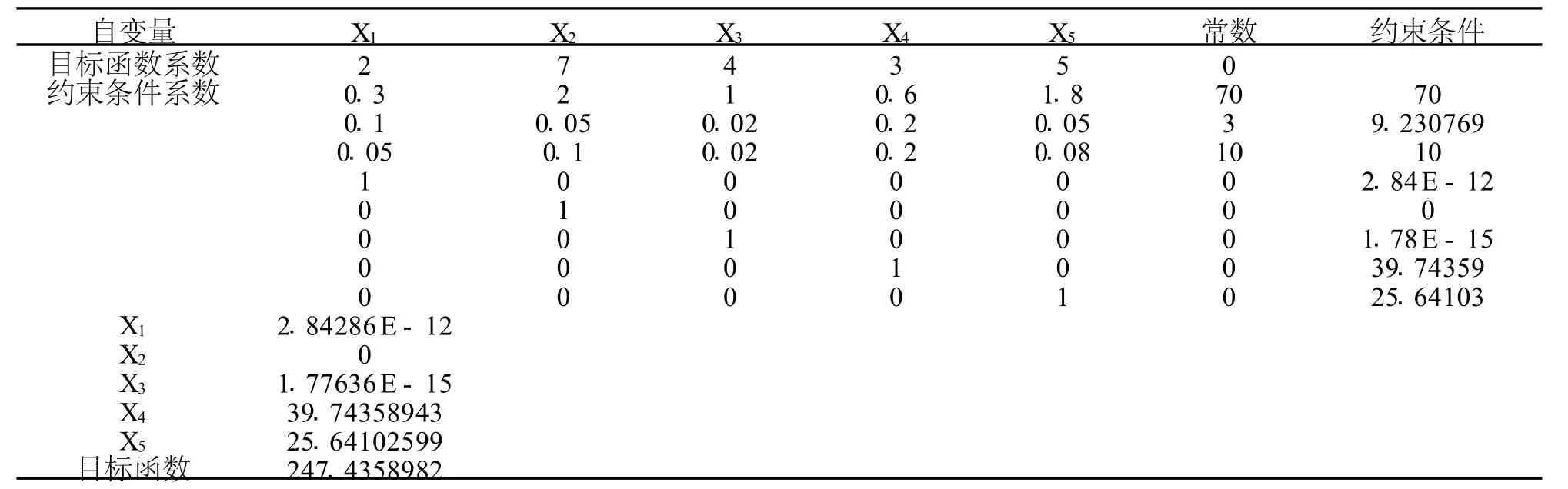
表2 EXCEL求解过程

从上求解过程可以得到最优解为：

X1=2.84286E-12,X2=0,X3=1.77636E-15,X4=39.74358943,X5=25.64102599,

目标函数的最优值为：247.4358982.

在整个求解过程中,需确定目标函数单元格及“可变单元格”区域位置两处单元格位置,当然要正确地输入约束条件和确定所求的目标是最大还是最小才可求得正确结果.但对于有无穷多最优解的问题,该方法只能给出其中的一个解[3].

2 用单纯形法求解

2.1 建立数学模型[4]

设Xj(j=1,2,3,4,5)表示10千克混合饲料中所含的第j种饲料的数量.

析约束条件：

当然对变量Xj(j=1,2,3,4,5)的要求应为非负.

目标函数：

min f=2 X1+7 X2+4 X3+3 X4+5 X5

数学模型：

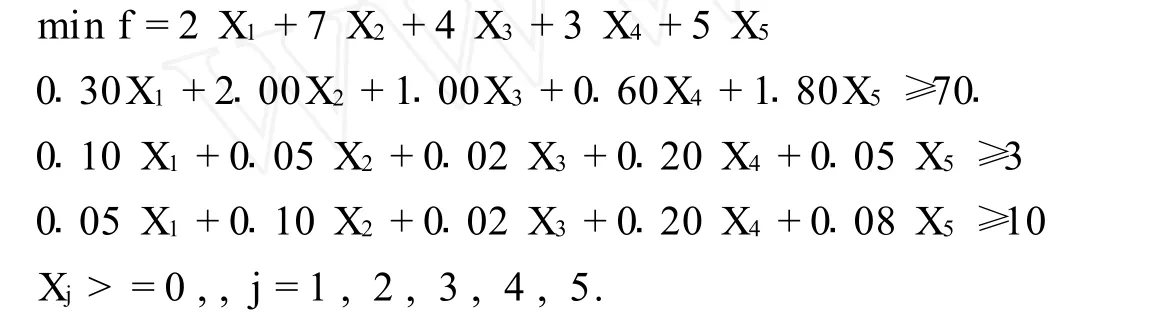
2.2 用单纯形法求解[5]

1)引入松弛变量将化标准形

在标准形中,约束条件的等式约束是一个含有5个变量、2个等式的线性方程组,系数矩阵的秩为2,所以有3个基变量,另外2个非基变量.

2)非基变量置0,求得一个基本可行解

3)建立初始单纯形表 (见表3)

将约束部分 (即线性方程组)的系数矩阵等式右边的常数、检验数以及目标函数值,填入表3中,得到某组基变量对应的单纯形表.

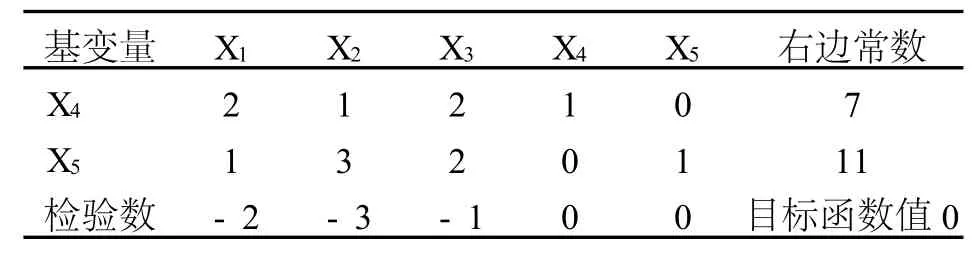
表3 初始单纯形表

4)初等变换

将转轴点变成1,并且以转轴点所在的行为基准行,将表中入基变量所在列的其他数包括检验数都变为0,结果就是新基变量对应的单纯形表 (见表4).

5)迭代,直到检验数非负,可得问题的最优解

表中检验数都大于等于0,所以已经是最优,它的最优解为X1=2,X2=3,X3=0,目标函数的最优值为max f=13(见表5)

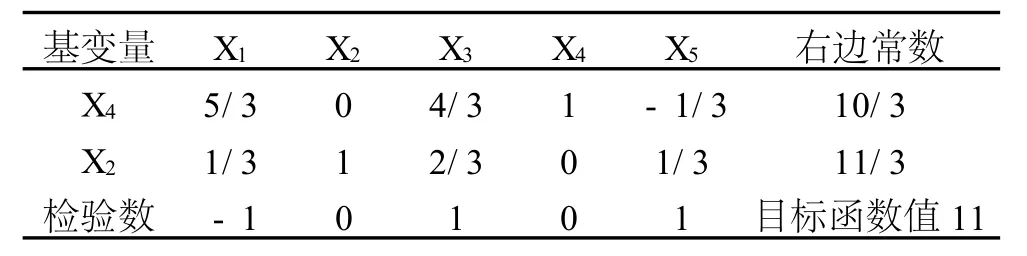
表4 关于新基的单纯形表

表5 最优解

3 用MA TLAB解决规划问题通用函数

MA TLAB是一种应用于数学计算及计算结果可视化处理的面向对象的高性能计算机语言,它以矩阵和向量为基本数据单位,从而提高程序的向量化程度,提高计算效率,尤其适合于线性规划、整数规划、多元规划、二次规划等规划类问题的算法的编写,以及数据拟合、参数估计、插值等数据处理法[6].

在以上算法的支持下,给出MA TLAB解决规划问题通用函数.

说明：

1)函数使用条件：全部变量、常数项非负,约束为不等式

2)函数参数说明：A为单纯形表,a为函数系数距阵,m和n分别为非基变量个数和基变量个数.

上函数可获得最佳的单元格的可能值,在数解决方案过程中的各个阶段使用线性近似值问题函数;这些近似值线性实际函数时都完全相同.

[1] 唐五湘,程桂枝.Excel在管理决策中的应用 [M].北京：电子工业出版社,2005：30-35

[2]张光澄.非线性最优化计算方法 [M].北京：高等教育出版社,2005：82-95

[3]谢金星,薛毅.优化建模LINDO/LINGO软件 [M].北京：清华大学出版社,2005：47-63

[4]赵静,但琦.数学建模与数学实验 [M].北京：高等教育出版社,2008：56-66

[5]李静萍,谢邦昌.多元统计分析方法与应用 [M].北京：中国人民大学出版社,2008：112-132

[6]张志涌,徐彦琴.MATLAB教程 [M].北京：北京航空航天大学出版社,2004：135-167