一种基于联合变换相关的PSF估计方法*

张 涛，王宏力，陆敬辉，姜 伟

(火箭军工程大学控制工程系，西安710025)

一种基于联合变换相关的PSF估计方法*

张 涛，王宏力*，陆敬辉，姜 伟

(火箭军工程大学控制工程系，西安710025)

针对弹体振动引起的星图成像质量退化的问题，提出了一种基于联合变换相关的PSF估计方法。首先，在低帧速CCD相机的曝光时间内，利用高帧速CCD相机拍摄得到振动条件下的连续平移星图序列，将星图序列的相邻帧拼接成联合输入星图;其次，采用联合变换光学相关器作为处理器并引入坐标变换进行相关运算，得到联合输入星图的相对位移矢量，插值处理后估计出模糊星图的连续PSF;最后进行仿真验证，仿真结果表明:联合变换相关法不仅有效克服了仅从单幅模糊星图估计PSF存在的多解问题，还较准确地估计出了由角振动引起的空间变化模糊星图的PSF。

图像处理;PSF估计;联合变换相关器;振动

星敏感器作为一种具有高测量精度的空间姿态光学敏感器，可为中远程弹道导弹提高准确的空间方位和姿态基准［1］。当捷联安装在弹体的星敏感器进行实时动态成像，除了受到光学系统的衍射、探测器采样、大气的扰动等因素影响外，复杂振动环境也降低了星敏感器成像质量，使得星体质心提取精度下降，甚至可能导致星敏感器无法正常完成定姿［2］。因此，如何处理弹体振动引起的星图模糊就成为了一个亟待解决的问题。

目前，许多学者处理星图模糊问题常使用的方法为星图复原法，它是一种软件处理方法，通过对星图进行后期处理消除振动模糊，且成本低，算法比较成熟。文献［3－6］虽然能使模糊星图达到较好的复原效果，但也存在两点不足:一是在PSF未知情况下，仅从单幅模糊星图估计出原始星图，相当于从1个已知条件求解2个未知数，会存在很多种PSF和复原结果，误差较大;二是假定星图受到匀速直线运动或者一维快速简谐振动影响，这种条件下造成的星图模糊属于空间不变模糊，而文章中并未对复杂角振动引起的空间变化模糊进行研究，存在一定局限性。

针对上述分析中存在的不足，本文提出了一种基于联合变换相关的PSF估计方法。该方法可以通过CCD相机拍摄的多帧星图中获得更多的星图信息，利用联合相关变换器得到比单帧星图更为准确的模糊星图PSF和更加满意的复原效果。此外，结合坐标变换，本文方法还可以较准确估算角振动引起的模糊星图PSF。

1 联合变换相关法原理

联合变换相关法是对参考星图和目标星图进行二维空间相关运算，根据相关函数的峰值位置确定目标星图相对于参考星图的位移量［7］。假定目标星图t(x，y)相对于参考星图r(x，y)在x、y方向上的振动偏移量为Δx、Δy。如图1所示，将两帧星图分别放置于(－a，0)和(a，0)，得到联合输入星图j(x，y)为:

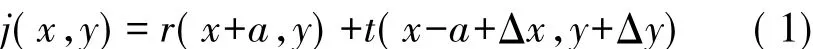
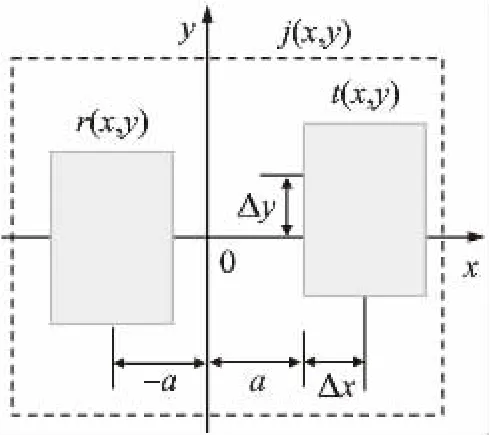
图1 联合输入星图

对j(x，y)进行一次傅里叶变换，得到其频谱函数

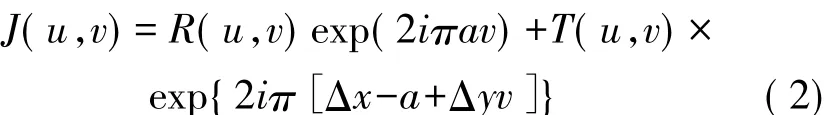
由式(2)可以得到联合变换功率谱|J(u，v)|2，表达式如下:

对功率谱|J(u，v)|2做傅里叶变换，便可得到联合相关输出:

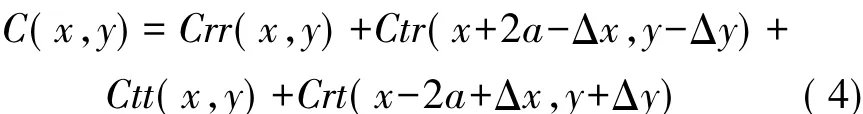
式(2)～式(4)中，R(u，v)、T(u，v)分别为r(x，y)、t(x，y)的傅里叶变换，R*(u，v)、T*(u，v)为R(u，v)、T(u，v)的复共轭。Crr(x，y)和Ctt(x，y)为自相关，中心坐标均位于(0，0);Ctr(x+2a－Δx，y－Δy)和Crt(x－2a+Δx，y+Δy)为互相关，中心坐标分别位于(Δx－2a，Δy)和(2a－Δx，－Δy)处。从式(4)可以看出，互相关信号包含了像移量Δx、Δy，通过检测和计算互相关峰相对理想位置(0，±2a)的偏移量，即可得到曝光时间内的像移量。联合变换相关法的计算流程如图2所示。

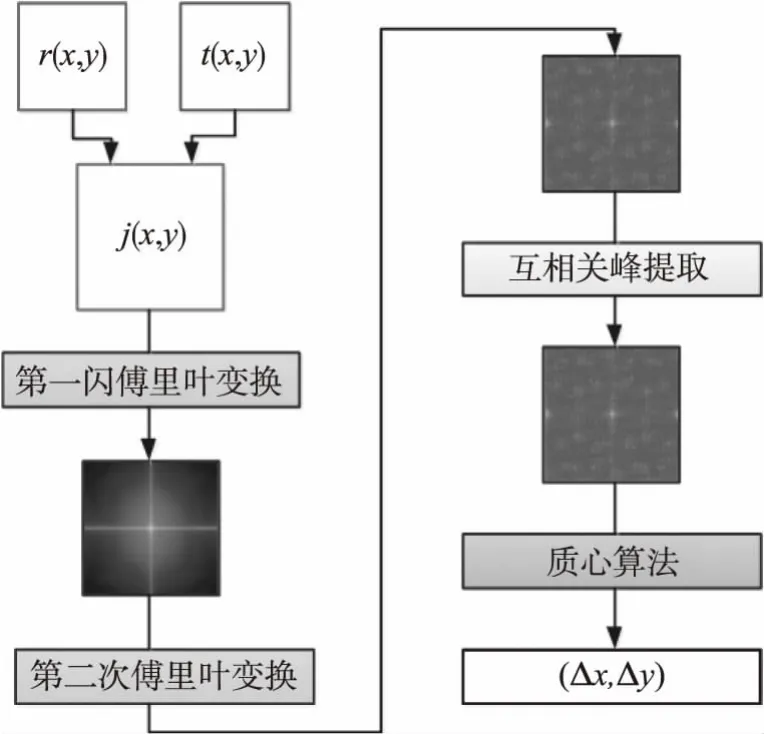
图2 联合变换相关法流程图

2 振动矢量估计

联合变换相关法具有很强的抗噪性能，针对低信噪比的星图也能较为准确的估计出亚像素位移量，但其缺点是运算量大，需要对联合星图做两次傅里叶变换，传统处理器难以实时处理，因此本文采用联合变换光学相关器JTOC(Joint Transform Optical Correlator)进行相关运算，其处理速度极快且功耗低［8］。图3是JTOC的原理图，其工作前提条件是增加1个与星敏感器CCD相机(本文特指低帧速相机)刚体连接的辅助高帧速CCD相机，二者同时成像时，由于高帧速相机曝光时间特别短，认为其获得的连续星图序列帧是清晰的，不存在模糊现象，而低帧速相机由于其曝光时间较长，获得的是一幅振动模糊星图。因为2个CCD相机是刚体连接，所以二者振动路径是一致的，而高帧速相机振动路径的可以从其拍摄到的序列帧中提取。JTOC具体工作过程2.1节会进行详细阐述。

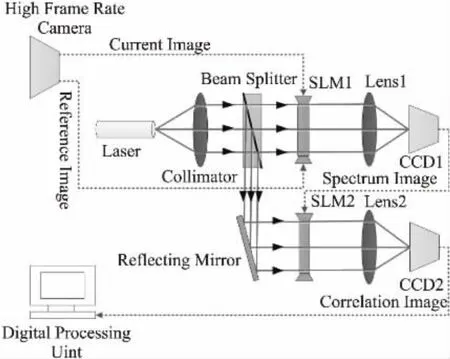
图3 联合变换光学相关器原理图

2.1 线振动矢量估计

线振动引起的星图模糊属于空间不变模糊，此时星图中所有像素点具有相同的振动轨迹。线振动矢量测量装置为联合变换相关器，如图3所示，具体步骤如下:

①在一个低帧速CCD相机曝光时间内，由另一个与其刚体连接的高帧速CCD相机捕获相邻的序列星图fi(x+a，y)和fi+1(x－a+Δx，y+Δy)，并排输入到空间光调制器 SLM1中作为联合输入星图j(x，y)。不妨假设fi(x+a，y)为参考星图r(x，y)，下一帧星图fi+1(x－a+Δx，y+Δy)为目标星图t(x，y);

②用准直的激光Laser照射SLM1上的联合星图j(x，y)，由于联合星图在傅里叶透镜Lens1的前焦平面上，在Lens1的后焦平面产生联合功率谱JPS (Joint Power Spectrum)星图，在CCD1上成像;

③读取CCD1上获取的联合星图功率谱至空间光调制器SLM2中，在此经过反射镜反射过来的激光进行调制，由傅里叶透镜Lens2再次变换后，在CCD2中成像，得到相关峰输出星图;

④根据获得的相关峰输出星图，利用质心搜索算法，得到互相关峰的真实坐标，即当前帧与下一帧的相对位移Δpipi+1(x，y)，其表达式如下:

式中:pi+1(x，y)和pi(x，y)表示2个互相关峰的坐标位置。

⑤不断用目标星图t(x，y)替换参考星图r(x，y)，重复步骤1～步骤4，可得到一系列相对星图位移序列{Δpipi+1(x，y)}，从而估算低帧速相机获取的模糊星图的振动路径。

2.2 角振动矢量估计

星敏感器成像过程中，除了受线振动的影响外，还有更为复杂的角振动。角振动引起的星图模糊，是一种空间可变模糊，它围绕1个圆心旋转，相对于静态星点，不仅产生了扩散，还存在一定旋转角度，星图模糊程度与距该圆心的距离有关。如果直接对角振动模糊星图运用2.1节中的方法检测振动路径，无疑存在较大的误差。因此，本文通过将星图在笛卡尔坐标下的角振动转换成极坐标下的线振动，然后将极坐标变化后的星图替代2.1节中的线振动的序列星图fi(x+a，y)和fi+1(x－a+Δx，y+Δy)，再使用联合变换相关器处理，便可准确估计出星图在极坐标下的系列位移矢量，根据坐标间转换关系，进而得到星图在笛卡尔坐标系下的旋转角度。下面具体推导笛卡尔坐标系与极坐标系的转换关系。

假设笛卡尔坐标系下的像素坐标为(x，y)表示，则极坐标变换可以表示为:

式中:r表示笛卡尔坐标系下矢量点对应的幅值，θ表示该矢量对应的幅角，取逆时针为正方向。

对式(6)进行逆变换得:

在笛卡尔坐标系下，用函数g1(x，y)表示CCD相机成像星图平面，将该星图平面逆时针旋转 φ度，得到平面g2(x，y)，g2(x，y)可表示为:

星图g1(x，y)和g2(x，y)经过极坐标变换后的星图分别用p1(r，θ)和p2(r，θ)表示，则有:

从式(9)可以知道，笛卡尔坐标系下星图平面的角振动转换成极坐标系下该星图在θ方向的线振动，并且二者的振动矢量存在对应关系。

根据上述分析，无论是线振动还是较为复杂的角振动，都可以通过联合变换相关器得到对应的振动矢量，这也为下一步振动星图的PSF估计奠定了基础。

3 PSF估计

利用联合变换相关法，可以得到高帧速CCD相机各相邻星图帧间的偏移量，这些偏移量是一系列离散值。相机的振动路径是连续的，相应的点扩散函数PSF也应该是连续的。因此，需要施加一些PSF满足的先验约束条件，通过约束实现离散的偏移量到连续的PSF之间的转变。PSF是一个能量分布函数，并与相机振动路径相关，不妨假设PSF是路径r(t)和能量e(t)的函数，其约束条件为:

①PSF函数h(x，y)满足能量守恒，则有:

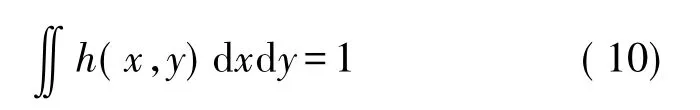
②相机振动路径是速度r'(t)和加速度r″(t)关于时间的函数，因此r(t)至少是一个t的二次函数。假设在低帧速CCD采集时间T内，场景辐射能量不变，则有约束条件:

从式(11)得出，在任意一段时间间隔 Δt内，CCD相机的能量累积和该段时间间隔长度成正比关系。

基于式(10)、式(11)，振动PSF的估计过程如图4所示。图4(a)的各个离散点表示每一帧星图相对于第1帧的绝对偏移量，即离散的振动矢量;图4(b)中取离散点前后两段曲线段的中点之间的曲线段作为对应帧星图的路径，即对振动路径r(t)上的离散点进行二次抛物插值，满足运动路径关于时间的二阶可导;图4(c)中由于等间隔曝光时间内，根据能量相等约束，故各矩形的面积是相等的，其高度与宽度成反比，而高度表示PSF值大小，因此便得到离散点对应的PSF中;图4(d)对PSF值进行归一化处理，使其满足式(10)约束条件，并进行插值拟合得到连续的PSF。

图4 PSF估计过程

4 仿真验证

为了验证本文联合变化相关法的有效性，首先设置星敏感器的参数，参见表1。

表1 星敏感器工作参数

根据参数可仿真得到参与实验的标准星图，其尺寸大小为512 pixel×512 pixel，如图5所示;其次设置高、低帧速相机的帧速比18∶1，高帧速相机拍摄得到的序列星图尺寸大小均为256×256，拼接完成的联合输入图像尺寸大小为1 024 pixel×1 024 pixel;最后对模糊星图进行复原，选用方法为RL算法［9］，并采用峰值信噪比［10］PSNR(Peak Signal-to-Noise Ratio)作为星图复原结果的客观评价标准。

图5 标准星图

4.1 线振动条件下仿真分析

对图(5)中的标准星图施加大小为10个像素，方向为水平方向的线振动位移量，模糊星图如图6所示。由高帧速相机拍摄获得的连续平移星图序列如图7所示，将相邻帧星图拼接成联合输入星图，得到图8，根据联合变换相关器的工作过程，则联合输入星图的相关峰输出如图9所示。

图6 模糊星图

图7 连续平移星图序列

图8 联合输入星图

图9 相关峰输出

由图9可知，互相关峰并不是一个独立亮点，因此需要在其整数像素位置周围取M×N的邻域，本文选10×10的邻域，然后利用质心搜索算法，得到互相关峰的真实坐标，进而通过式(5)可得到一系列离散的位移序列，插值处理后便估计出了模糊星图的连续PSF。根据得到的PSF，利用RL算法反卷积后得到复原星图(图10)。

图10 RL复原星图

由图6和图10可以直观看出复原效果很明显，并且，相对于模糊星图，复原后的星图PSNR提高26.50%，这说明利用联合变换相关法估计的线振动条件下的PSF较准确。

4.2 角振动条件下仿真分析

仍然以图4中的标准星图作为原始星图，对其施加角度为0.04 rad的角振动位移量，模糊星图如图11所示。角振动条件下的仿真分析类似于4.1节，不同之处在于要将高帧速相机拍摄的星图经过坐标转换得到极坐标系下的星图，然后用转换后的星图序列拼接成联合输入星图进行后续的仿真实验。由于本文篇幅有限，因此只给出模糊星图、笛卡尔坐标系下的连续平移星图序列、极坐标系下的连续平移星图序列以及RL复原后的星图，分别如图11～图14所示。

图11 模糊星图

图12 笛卡尔坐标系下的连续平移

图13 极坐标系下的连续平移

图14 RL复原星图

由图11和图14可以直观看出复原效果很明显，并且，相对于模糊星图，复原后的星图PSNR提高33.60%，说明利用联合变换相关法同样可以较准确的估计角振动条件下的PSF。

5 结束语

本文针对弹体振动引起的星图成像质量退化的问题，提出了一种基于联合变换相关的PSF估计方法。通过引入联合变换光学相关器和坐标变换对联合输入星图进行相关运算，将得到的一系列相对位移矢量插值处理后估计出模糊星图的连续PSF，并分别在线振动和角振动条件下，对算法有效性进行了仿真验证。联合变换相关法不仅有效克服了仅从单幅模糊星图估计PSF存在的多解问题，还较准确地估计出了由角振动引起的空间变化模糊星图的PSF。

［1］ 孙高飞，张国玉，刘石，等.高精度背景可控星图模拟器设计［J］.红外与激光工程，2015，44(7):2196－2199.

［2］ 邓长智，王宏力，陆敬辉，等.低频振动对星敏感器成像影响分析［J］.传感器与微系统，2014，34(1):43－46.

［3］ 黄博.临近空间高动态星图仿真技术研究［D］.武汉:华中科技大学，2012.

［4］ 韩礼，张力军，蔡洪，等.基于维纳滤波的运动模糊星图复原仿真分析［J］.光学技术，2014，40(4):316－320.

［5］ 吴小娟，王新龙.星图运动模糊及其复原方法［J］.北京航天航空大学学报，2011，37(11):1338－1342.

［6］ 徐沪萍，付文兴，马杰.一种遥感图像振动模糊复原方法［J］.华中科技大学学报，2014，42(3):28－32.

［7］ 许博谦.星载相机微振动下图像补偿技术研究［D］.长春:中国科学院长春光学精密机械与物理研究所，2015.

［8］ 易红伟，赵惠，汶德胜，等.联合变换相关器像移测量静态仿真实验分析［J］.光学学报，2010，30(12):3471－3475.

［9］ Qiao S，Wang Q，Sun J N，et al.A New Method by Steering Kernel-Based Richardson-Lucy Algorithm for Neutron Imaging Restoration［J］.Nuclear Instruments and Methods in Physics Research Section A:Accelerators，Spectrometers，Detectors and Associate Equipment，2014，735:541－545.

［10］王辉，吴钦章.基于图像质量评价的自动图像复原技术［J］.传感技术学报，2012，25(7):930－935.

张 涛(1992－)，男，江西上饶人，硕士研究生，主要从事星敏感器测量精度研究;

王宏力(1965－)，男，陕西凤翔人，教授，博士，主要研究方向为导航制导与控制、复合制导、天文/惯性导航、故障诊断及可靠性评估，775128700@qq.com。

PSF Evaluation Method Based on Joint Transform Correlation*

ZHANG Tao，WANG Hongli*，LU Jinghui，JIANG Wei
(Department of Control Engineering，Rocket Force University of Engineering，Xi’an 710025，China)

Point Spread Function(PSF)estimation，a method based on joint transform correlation，is put forward to resolve the quality deterioration of the star image imaging resulted from the vibration of missile body.Firstly，within the exposure time of low frame rate CCD camera，a high frame rate CCD camera is used to obtain a continuously translational star image sequence under the condition of vibration;then the consecutive frames of the star image sequence are spliced into a joint input star image.Secondly，joint transform optical correlator is introduced into coordinate transformation as the processor to obtain the relative displacement vector of joint input star image;then interpolation processing is conducted and the consecutive PSF of the fuzzy star image is estimated out.Finally，simulation verification is completed.Results of simulation verification indicate that joint transform correlation method not only effectively overcomes the shortcomings of single fuzzy star image，but also accurately estimates out the PSF of fuzzy star image of spatial transform resulted from angle vibration.

image processing;PSF evaluation;joint transform correlator;vibration

V271.4

A

1004－1699(2017)02－060－06

C:6140;6135

10.3969/j.issn.1004－1699.2017.02.016

项目来源:陕西省科学技术研究发展基金项目(2014JM2－6107)

2016－04－07 修改日期:2016－07－26