利用破产概率分析彩票中的风险问题

梅 瑞,张 超,张伟华

(1.河北北方学院理学院,河北张家口075000;2.北京北大方正软件技术学院,河北廊坊065001)

1 彩票问题的介绍

目前彩票飓风席卷全国大地,很多人为了获得巨额的回报纷纷加入到彩民的行列.彩票的发行方式和发行种类越来越多,其中最为流行的当数“传统型”与“乐透型”.它们一般都是从一些特定的数字中选出一定数量的数字构成一注,然后与摇出的中奖号码对照确定相应的中奖等级.

随着彩票的不断发展,其中所蕴含的数学问题也逐渐引起了许多专家学者的兴趣,2002年的全国大学生数学建模竞赛就恰恰是以“彩票中的数学”作为参赛课题.彩票的中奖对彩民来说是极大的喜悦,然而这仅仅是一种偶然,其中包含着许多概率统计的知识,所以人们一开始的研究也只是集中在计算各等奖项的中奖及特殊情况的中奖概率.例如[1-3],邹植民,尹铁开研究了电脑福利彩票中奖号码连号的概率.随着对彩票关注程度的提高,大多数人把目光集中到了对彩票方案的评价上,主要是通过构造一个效用函数或判别函数来比较奖金额与中奖概率对彩民的吸引力,以衡量彩票的方案并给出建设性意见.例如,刘世民[4]等人就把彩票方案的优劣归结为其对彩民吸引力的大小,通过构造经济中常用的效用函数,把总的吸引力归结为奖金额与中奖概率加权作用的结果进而用层次分析法和熵值法确定相应的权值对多种方案进行了评价.

彩票公司把每一期的销售总额按比例分成两部分,一部分留作奖金,另一部分则用于福利事业.彩票在奖项的设置上分为高项奖与低项奖,低项奖的奖金一般是固定的,而高项奖的奖金则是除去所有低项奖后按一定的比例分配.如果某一期高项奖落空相应金额会流入奖池中,加入到下一期的奖金分配.购买彩票中大奖实际是大多数人成就了少数人获得巨额回报的喜悦.从长远来看彩民的资金是部分返还给彩民,表面上彩票公司是收入大于支出不存在什么风险,可问题恰恰出现在一等奖的设置上.一般而言,一等奖都会设有金额的上下限,当中一等奖的人数过多时,就会出现每个人分得一等奖金额小于下限.这时彩票公司就要进行补偿,而当这个补偿大到一定程度时,彩票公司就会出现支出大于收入的情况.上述情况似乎是很少发生,但它总会是以正概率出现,说明彩票公司的确是面临着风险,这点也是本文研究彩票公司破产概率的意义所在.

2 彩票破产分析及相关符号

为了叙述的方便,约定下列记号:

Pi表示第i等奖的中奖概率,Ni奖的中奖数目,bi为第i等高项奖的分配比例i=1,2,3,mi为第i等奖的单注金额,S为总奖金额,M为销售总额,M′为奖池中的金额,N为一期的投注数.

这里需要指出的是 N一般是随机的,可为了研究方便用它的期望n(E[N]=n)来替代 N,并且n足够大.Ni,i=1,2,…,k为一些随机变量,它们服从参数为 (n,pi)的二项分布 (B (n,pi))[5].由假设 (2)可知,B (n,pi)i=1,2,…,k是相互独立的.

为了研究彩票中的风险问题,做出一些假设,建立数学模型:①总奖金占总销售额的比例为 r,投注者单注金额为e元;②若已得到高级别的奖,则不再兼得低等奖;③总共有k项奖,其中一、二、三等奖为高项奖,后面的为低项奖,低项奖的奖金固定,高项奖按比例分配;④一等奖单注保底金额为l元,封顶金额为 u元,若一等奖奖金不足l元时,则需要补足;⑤若某一期的高项奖没有领取,则自动流入下期一次累计,这样奖池中存在一定数目的金额.

以上的假设都是从现实的彩票规则中抽象出来,具有很好的代表性和合理性.

3 彩票的破产概率[6]

如同在精算学中对保险公司破产的分析,本节也将研究彩票公司在某一期彩票发行时导致支出大于收入的概率.

彩票公司每发行一期彩票就会得到一笔销售资金M,同时支出一笔资金S作为奖金,而在奖池中也存在一定数目的资金M′,当S-M-M′＞0发生时,本期的彩票发行就宣告破产.

就是彩票的破产概率.

对于高等奖的奖金有如下的计算方法:

当l≤E[m1]≤u或E[M1]＞u时,M r就全部作为奖金返还给彩民,这是彩票公司不会面临破产,而当 E[m1]＜l时,彩票公司就要对一等奖的奖金进行补偿,在这种情况下我们就需要关注概率(1).而由假设可知彩票公司并不是把所有的销售资金用作奖金,其中的 Mr作为奖金,剩余的用于福利事业.所以说对于 (1)式可以等价为

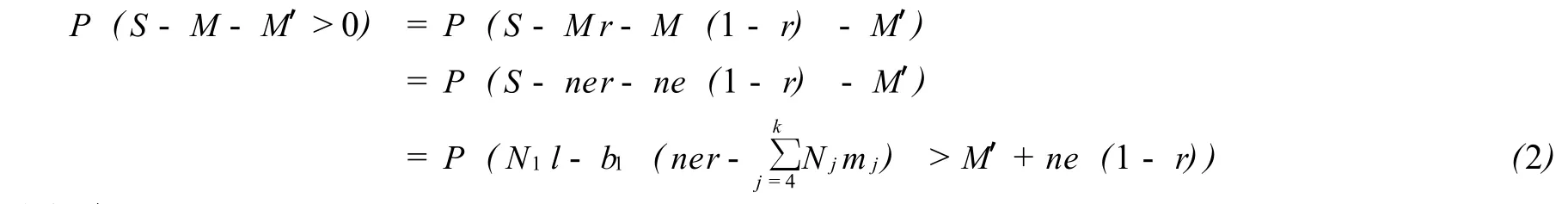
关于 (2)我们有

定理1 (2)式的概率函数为

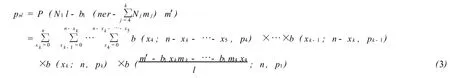
其中b(xi;n-▯,pi),i=1,4,…,k表示二项分布B (n-▯,pi),i=1,4,…,k的概率函数,▯表示 (3)中任意的 xk,xk+xk-1……xk+xk-1+…+x5.

由上式可直接得出 (3)式.

推论1 由定理1可得

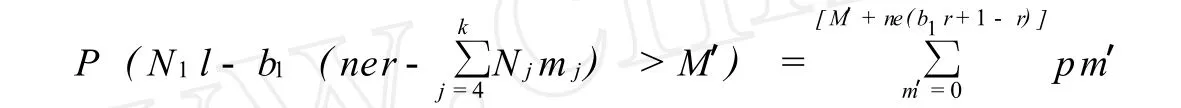
其中 [M′+ne(b1r+1-r)]是指 M′+ne(b1r+1-r)的整数部分.

对于 (2)_式,表达过于复杂,可以用下面的式子来近似它:

下面可由克尔科夫 (Markov)不等式[7],得到 (2)式的一个上界.

定理2 对于彩票破产概率 (2),可以得到一个上界,即

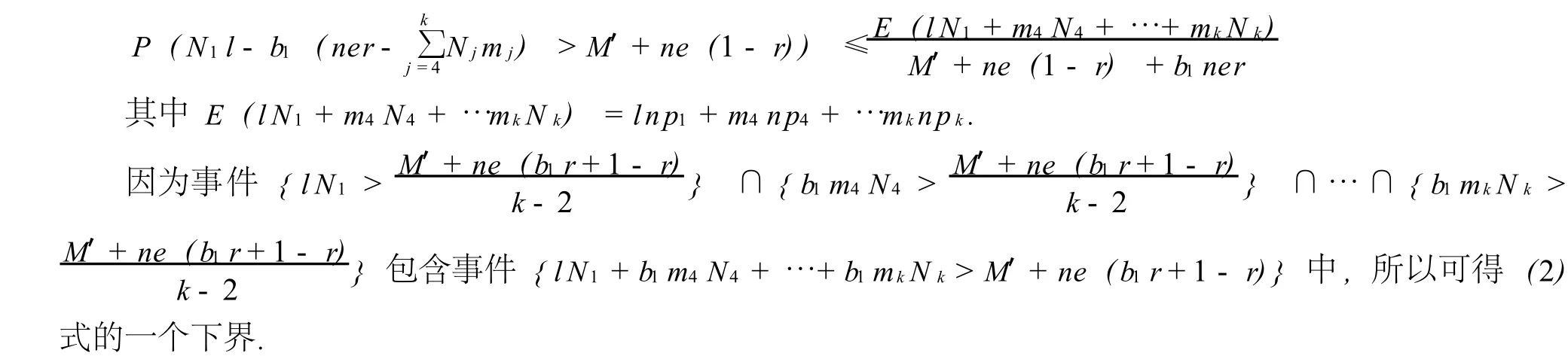
定理3 彩票破产概率 (2)的一个下界表达如下

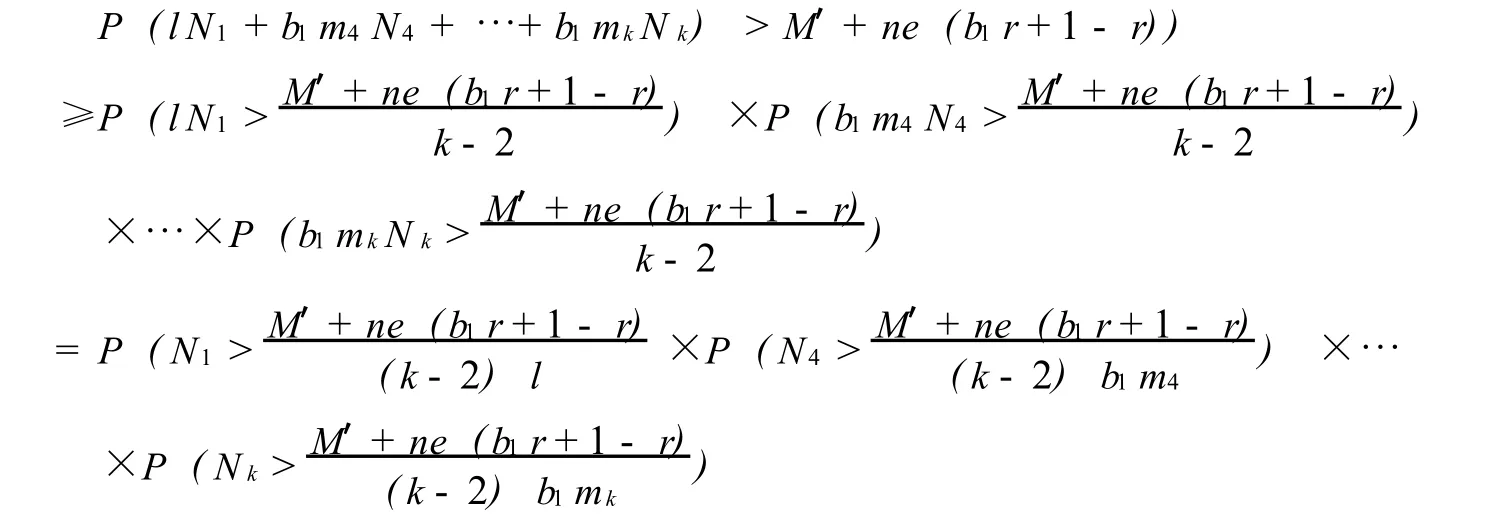
下面再介绍 (2)式的一个下界.

定理4 彩票破产概率 (2)的一个下界表达如下

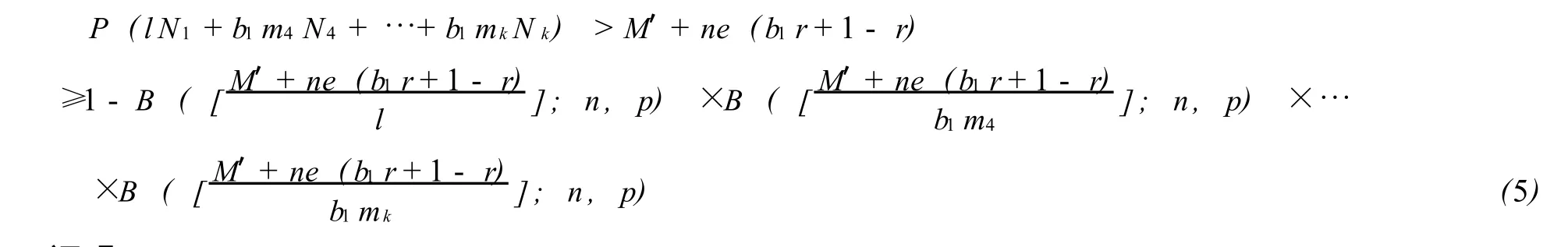
证明

对于 (4)、(5)式,可以用更简单的形式表达,不过首先要介绍一些知识作为铺垫.

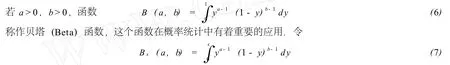
其中0＜x＜1,a＞0,b＞0为参数,由 (7)式定义的函数称为不完全贝塔函数.通过 (6)式和 (7)式,可以定义一个非常重要的工具,即不完全贝塔函数比,具体表达如下

于是对二项分布的分布函数B(x;n,p),就有

引理1 二项分布的分布函数B(x;n,p)与不完全贝塔函数比有如下关系:

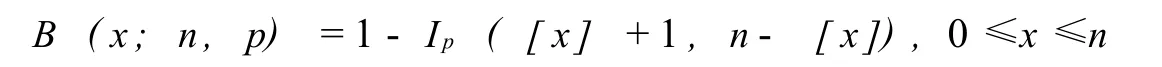
关于引理1的具体证明可参照方开泰[8]等.

由定理3及引理1可得 (4)式的一个简化表达式,即

推论2

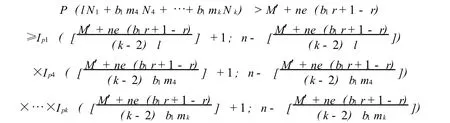
由定理4及引理1可得 (5)式的一个简化表达式,即

推论3

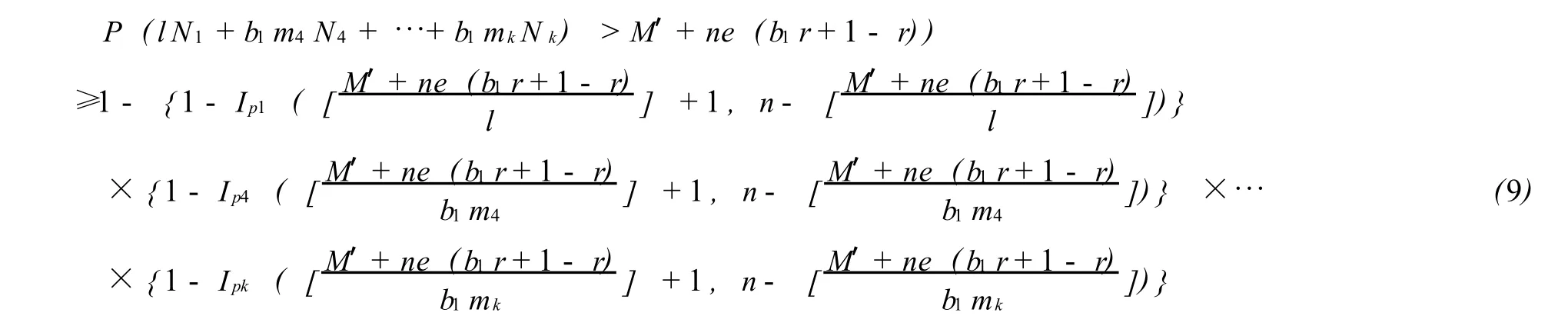
4 结 论

通过上述讨论得到彩票破产概率的上、下界,如果破产概率满足l≤E[m1]≤u或 E[m1]＞u,则彩票公司不会面临破产,如果 E[m1]＜l,破产概率函数可通过分析二项分布函数与不完全贝塔函数关系得到,彩票公司就会出现破产的风险.

[1] 邹植民,尹铁开.电脑福利彩票中奖号码连号的概率 [J].数理统计与管理,2006,25(04)：4-5

[2] 袁博,左振钊,张艳红.证券投资中的风险分析 [J].河北北方学院学报,2008,24(01)：73-76

[3] 雷晓军,梁治安.证券组合投资模型优化 [J].商场现代化,2007,8(03)：170-172

[4] 刘世民,王进.彩票方案的评价 [J].工程数学学报,2003,2(05)：74-80

[5] 李灿,郭尊光.浅谈二项分布的近似计算 [J].科技情报开发与经济,2009,14(69)：16-19

[6] 马学思,刘次华.变破产下限风险模型的破产概率 [J].数理统计与管理,2007,3(09)：70-73

[7] Ross SM.Introduction to Probability Models[M].USA：Academic Press,2003：30-75

[8] 方开泰,许建伦.统计分布 [M].北京：科学出版社,1987：72-89