弱各向异性介质地震波传播特征分析
2010-01-12余世新
苏 云,李 军,唐 娟,黄 倩,余世新
(1.成都理工大学 信息工程学院,四川成都 610059;2.中国石油化工股份有限公司 江汉油田分公司物探研究院,湖北潜江 433100)
0 前言
在地质模型研究的过程中,模型由最初的弹性各向同性模型,粘弹性各向同性模型,发展到后来的弹性各向异性介质,粘弹性各向异性模型[1~5]。与各向同性介质相比,各向异性介质中的地震波传播规律要复杂很多,同时携带的信息也更为丰富,因此对各向异性地层的地震波传播特性研究,具有重大的价值[6]。在弹性各向异性介质中,波的传播方向和质点振动方向,不存在简单的垂直或平行关系,即波的传播不是纯纵波或纯横波的模式,表现为波的群速度与相速度不一致[7]。Thomsen[8]导出VTI三类体波的相速度解析表达式,其中定义了三个参数描述速度随方向的变化,二个参数ε和δ用于qP波和qSV波的近似速度解,一个参数γ用于qSH波的严格速度解[8],Thomsen参数及简易的速度表达式,已被地震勘探学术界和产业界广泛接受。Sena在Thomsen工作的基础上,通过线性近似的方法,推导出关于射线角的群速度公式;Tsvankin[9]年推导了各向异性介质中群速度与相速度的关系式。作者在本文利用Thomsen提出的弱各向异性理论,分析了各向异性参数对qP波、qSV波和qSH波的相速度和群速度的影响。
1 VTI介质相速度与群速度
Thomsen[8]把描述横向各向同性介质(VTI介质)性质的五个弹性各向异性模量,重新组合成其它五个参数,即垂直各向同性平面的qP波和qSV波速度α、β,以及三个无量纲的Thomsen各向异性参数ε、δ、γ。由Thomsen理论,在弱各向异性假设下,得到由上述五个转换参数表示的qP波、qSV波、qSH波相速度近似表达式(1)。

从式(1)可以看出,采用各向异性参数ε、δ、γ描述弱各向异性介质中波的相速度,可以大大简化相速度方程,使得相速度随相角的变化更为直观。
由Berryman理论[10],群速度VG的标量大小与相速度V的标量大小之间的关系为:
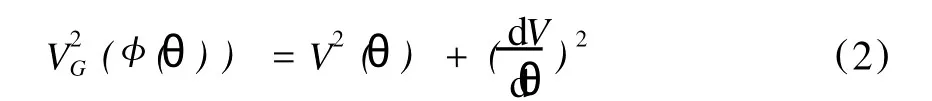
相速度的导数表达式为:

值得注意的是:相速度V是相角θ的函数,而群速度VG必须由群角φ标定,但不一定是群角φ的函数,因为由于qSV波群速度交会区的存在,一个群角可能对应二个以上群速度值。
通过线性的近似,相位角和群角之间的关系如下:
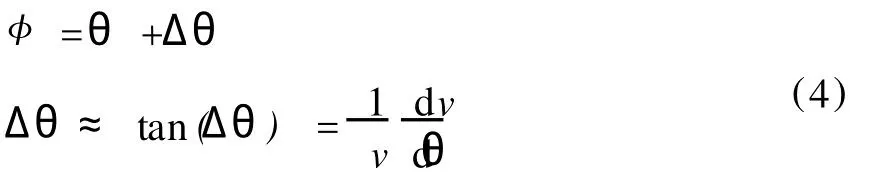
式中 φ为群角;v为相速度;Δ θ为群相偏离角。
可以看出式(3)、式(4)共同定义了各种类型波在任意角度的群速度。
2 数值模拟
为了更好地理解相位角和相速度、群角和群速度之间的关系,以及Thomsen各向异性参数对相速度、群速度的影响,下面用理论模型分析弱各向异性VTI介质中,qP波、qSV波和qSH波的传播特征。通过只改变各向异性参数的某一个值,观测
qP波、qSV波和qSH波的相速度随相位角,群速度随群角变化的情况。
2.1 Thomsen参数变化对地震波的相速度的影响
建立模型参数如表1~表3所示。
图1(见下页)为不同各向异性参数ε、qP波和qSV波的相速度,随相位角变化情况;图2(见下页)为不同各向异性参数δ、qP波和qSV波的相速度随相位角变化情况;图3(见下页)为不同各向异性参数γ和qSH波的相速度随相位角变化情况,考虑图像的对称性,仅对图像中θ在[0,π/2]的区间内的情况进行讨论。

表1 各向异性介质中模型介质参数(ε变化)Tab.1 Media parameters of anisotropic media model(εchanges)

表2 各向异性介质中模型介质参数(δ变化)Tab.2 Media parameters of anisotropic media model(δchanges)
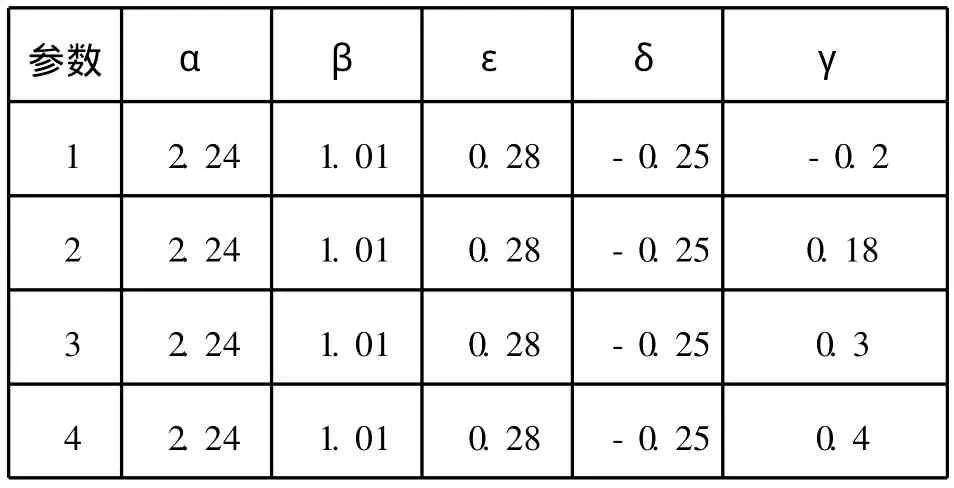
表3 各向异性介质中模型介质参数(γ变化)Tab.3 Media parameters of anisotropic media model(γchanges)
从下页图1中可以看出,当ε取值分别为0、0.1、0.2、0.3时,在θ=0°附近ε变化对qP波相速度曲线没有影响,当θ逐渐增加时,特别是当θ在π/6到π/2之间,ε变化对qP波相速度曲线的影响越来越明显,在θ=π/2时达到最大。在θ=0°和θ=π/2处,ε变化不会影响qSV波相速度曲线,随着角度逐渐趋向θ=π/4时,相速度体现出的各向异性更加明显。
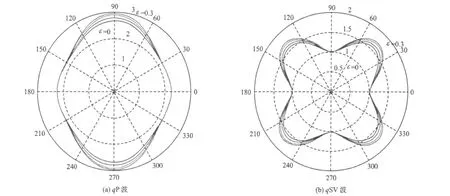
图1 参数ε的变化对qP波、qSV波相速度的影响Fig.1 The effects of parametersεon the phase velocity ofqP-wave andqSV-wave
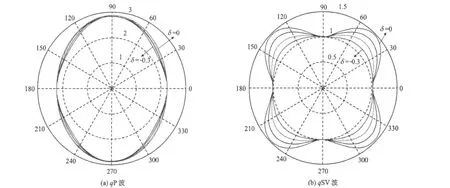
图2 参数δ的变化对qP波、qSV波相速度的影响Fig.2 The effects of parametersδon the phase velocity ofqP-wave andqSV-wave
从图2中可以看出:θ在0和π/2附近,δ的变化对qP波的相速度的影响不大。而在其余的角度范围内,可以看出δ对qP波的相速度的影响,尤其是在π/4附近,影响更为明显。在θ=0°和θ=π/2处,δ变化不影响qSV波相速度曲线,随着角度逐渐趋向θ=π/4时,相速度体现出的各向异性更加明显。
从图3中可以看出:当γ取值分别为-0.2、0.18、0.3、0.4时,在θ=00附近时,γ变化对qSH波相速度曲线没有影响。当θ逐渐增加时,γ变化对qSH波相速度曲线的影响越来越明显,在θ=π/2时达到最大。

图3 参数γ的变化对qSH波相速度的影响Fig.3 The effects of parametersγon the phase velocity ofqSH-wave
2.2 Thomsen参数变化对地震波的群速度的影响
采用表1~表3的模型参数,改变各向异性参数的某一个值,观测qP波、qSV波和qSH波的相速度随相位角、群速度随群角变化的情况,计算结果见图4~图8(见下页)。在图4~图8中,实线表示相速度,虚线表示群速度。考虑图像的对称性,仅对图像中θ在[0,π/2]的区间内的情况进行讨论。
从图4中可以看出:随着ε取值的不断增加,qP波的相速度曲线在θ=π/2附近的各向异性性质越来越强,这说明在大角度时,qP波相速度的各向异性主要由ε来控制。而群速度曲线在θ=π/2附近,随着ε的增加逐渐出现交叉区,这是因为群速速度与群角之间不是简单的函数关系,即不是在所有情况下都存在一一对应的关系,所以在群速度极坐标图中,可能会出现一个群角对应多个群速度值的情况,因此就会出现群速度曲线的交会区。群速度是波前面传播的速度,即是波的能量传播的速度。在各向异性介质中,群速度曲线的交会区处是能量的集中区域,并且交会区形态可以反映介质的各向异性程度。因此,随着ε取值的不断增加,qP波的群速度在θ=π/2附近的各向异性较为明显,与相速度曲线的规律基本相同。

图4 参数ε的变化对qP波相速度(实线)、群速度(虚线)的影响Fig.4 The effects of parameterεon phase velocity(solid line)and group velocity(dotted line)ofqP-wave

图5 参数ε的变化对qSV波相速度(实线)、群速度(虚线)的影响Fig.5 The effects of parameterεon phase velocity(solid line)and group velocity(dotted line)ofqSV-wave

图6 参数δ的变化对qP波相速度(实线)、群速度(虚线)的影响Fig.6 The effects of parameterδon phase velocity(solid line)and group velocity(dotted line)ofqP-wave
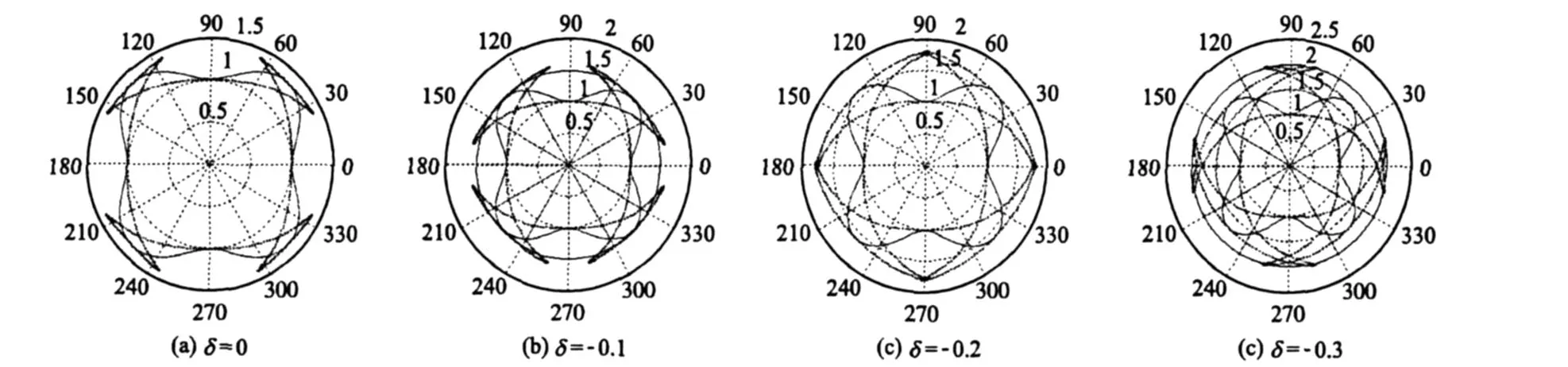
图7 参数δ的变化对qSV波相速度(实线)、群速度(虚线)的影响Fig.7 The effects of parameterδon phase velocity(solid line)and group velocity(dotted line)ofqSV-wave
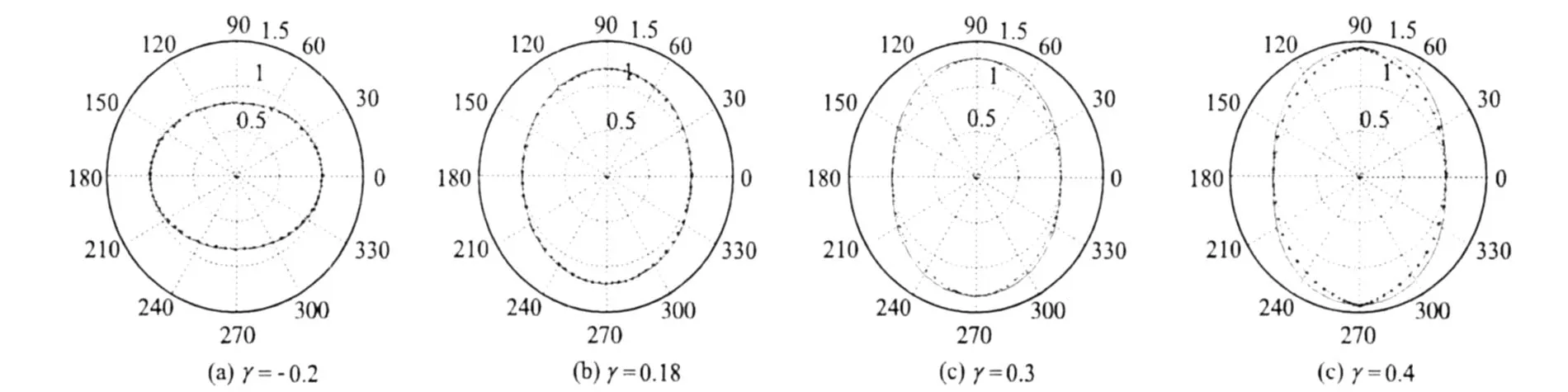
图8 参数γ的变化对qSH波相速度(实线)、群速度(虚线)的影响Fig.8 The effects of parameterγon phase velocity(solid line)and group velocity(dotted line)ofqSH-wave
从图5中可以看出,qSV波的群速度出现复杂的交会区形态,并且随着各向异性参数ε的增加,交会区形态会越来越复杂,且qSV波的群速度变化比相速度变化更为明显。
从图6中可以看出,随着δ值的减小,qP波相速度曲线在小角度范围内逐渐减少,qP波群速度在小角度范围内的变化趋势,与相速度曲线变化规律基本相同。并且,随着δ值的减小,qP波群速度在θ=π/2附近交会形态越来越明显。
从图7中可以看出,qSV波的群速度出现复杂的交会区形态。即随着δ的不断减小,交会区形态会越来越复杂,且qSV波的群速度变化比相速度变化更为明显。
从图8中可以看出,随着γ取值的不断增加,qSH波的相速度曲线在θ=π/2附近的各向异性性质越来越强。这说明在大角度时,qSH波相速度的各向异性主要由γ来控制;而在群速度曲线在θ=π/2附近,随着γ的增加会逐渐出现交叉区,但不是很明显。
3 结论
在各向异性介质中,地震波传播的相位角和群角不再相等,相速度和群速度也不完全一致。作者在本文中Thomsen提出的VTI三类体波的相速度解析表达式基础上,利用线性关系,推导了群角与相角之间的关系,以及群速度的解析表达式。通过数值模拟,改变各向异性参数,分析了各向异性参数对VTI介质相速度、群速度的影响。通过分析可知:参数ε影响qP波大角度传播的各向异性;参数δ影响qP波中小角度传播时的各向异性;(ε-δ)影响qSV波中等角度传播时的各向异性;参数γ影响qSH波大角度传播的各向异性;当各向异性参数变化时,群速度的各向异性要比相速度的各向异性明显,并且会出现复杂的交会区。
[1] TSVANK IN I.Reflection moveout and parameter estimation for horizontal transverse isotropy[J].Geophysics,1997a,62(2):614.
[2] WH ITE J E.Computed waveforms in transversely isotropic media[J].Geophysics,1982,47(5):64.
[3] CARC IONE J M,KOSLOFF D,KOSLOFF R.Wave propagation simulation in a linear viscoacoustic medium[J].Geophys J R.astr Soc,1988,95(3):597.
[4] 郭智奇,刘财,杨宝俊,等.粘弹各向异性介质中地震波场模拟与特征[J].地球物理学进展,2007,22(3):800.
[5] 郭智奇.粘弹各向异性介质波场模拟与储层信息研究[D].长春:吉林大学,2008.
[6] 赵峰帆,韩立国,林炎,等.TTI介质相速度理论研究[J].吉林大学学报(地球科学版),2006,36(专辑):121.
[7] 韩颜颜,郭智奇,刘财,等.弹性各向异性介质速度特征分析[J].吉林大学学报(地球科学版),2008,38(增刊):80.
[8] THOMSEN L.Weak elastic anisotropy[J].Geophysics,1986,51(10):1954.
[9] TSVANK IN I.seismic signatures and analysis of reflection data in anisotropic media[M].Pergamon,2001.
[10]BERRY MAN J G.Long-Wave elastic anisotropy produced by horizontal layering[J].Geophys Res.,1979,67(11):4427.
