VTI介质转换波速度分析方法研究及应用

斯兴焱,李录明,罗省贤

(“油气藏地质及开发工程”国家重点实验室 成都理工大学,地球探测与信息技术教育部重点实验室,四川成都 610059)

0 前言

当地层存在各向异性时,地震波的传播速度与传播方向有关,时距曲线会变得更加复杂,加大了转换波时距曲线的非双曲效应。国内、外很多学者对具有垂直对称轴的横向各向同性(VTI)介质的时距曲线进行了深入的研究,Tsvankin和Thomsen[1]用泰勒级数展开法,推导出了P-SV转换波(以下简称C波)单层和多层VTI介质的时距曲线方程。沿用1994年的思路,在1999年Thomsen[2]推导出了各向异性介质转换波高阶泰勒级数逼近的时距曲线方程,但炮检距与深度之比却限制在1.0范围以内。在2003年Xiang-Yang Li和Jianxin Yuan[3]对其做了修正,使得炮检距与深度之比扩大到了2.0,从而奠定了各向异性介质C波处理的理论基础。

但是,在XY-Li方程中,建立C波叠加速度模型转换为四个参数的求取问题,这就增加了处理成本和处理难度。作者在本文总结了双参数扫描法进行参数估计所应遵循的原则,分析各参数对时距曲线的敏感性及影响,分析用该方程进行参数估计的难度,以及该方程不同的简化形式,最终形成了一套合适的C波处理流程。通过批量处理和交互结合的方式,求取较精确的C波叠加速度模型。

1 方法原理

VTI介质C波时距曲线可以写成[3]:

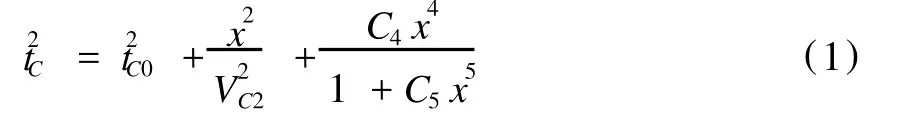
其中

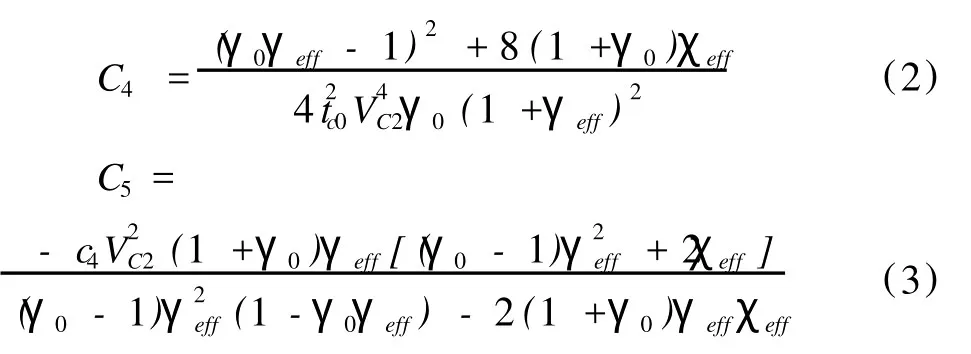
其中 tC为偏移距在x处的旅行时;tC0为零偏移距双程旅行时;VC2为动校正速度;γ0和γeff分别为纵横波垂直速度比和等效速度比;χeff为各向异性系数。该方程在偏移距与深度之比x/z<2.0时是精确的。

对于C波速度分析问题,即为求取这四个参数的问题。因此,有必要分析各个参数对于时距曲线有何影响,以便采取合适的方法求出各个参数,建立合理的叠加速度模型。

1.1 参数敏感性及参数估计方法

VC2对时距曲线的影响最大,它控制着时距曲线的双曲部份。如果VC2求取的不准确,将会导致其它三个参数求取的不准确。

表1为VTI三层介质模型参数。

图1是根据该模型正演的C波时距曲线。当小炮检距时,双曲近似可以很好的拟合时距曲线,所以可以将x/z限制在一定的范围内(通常取x/z<0.7)用双曲近似扫描,这样可以求得粗略的VC2。但转换波通常在炮检距较大时才产生,所以此法与实际情况是矛盾的,特别是在浅层,叠加次数太少,更是降低了求取精度。

图1 三层VTI介质C波时距曲线Fig.1 Synthetic c-wave gather for three-layer model of VTImedia

当χeff=0,γ0=γeff=1时,时距曲线方程与P波时距曲线方程相同,为双曲线。由此可见,γ0和γeff的影响不容忽视。它们对时距曲线的影响较VC2次之,控制着时距曲线的中等炮检距部份。当tC0、VC2和χeff给定时,双参数扫描γ0和γeff,分辨率和精度不高,如图2所示。

当γ0、γeff给定,双参数扫描VC2和χeff可以获得较好的分辨率和较高的精度[3],如图3所示,从图3中可见误差小于1%。

各向异性系数χeff对时距曲线的影响小,控制着时距曲线的大炮检距部份。一般χeff越大,旅行时越小。在tC0、γ0和γeff确定的情况下,可以通过双参数扫描VC2和χeff获得较高的分辨率和精度。如图3所示。

图2 γ0、γeff双参数扫描Fig.2 Double-scanning forγ0、γeff

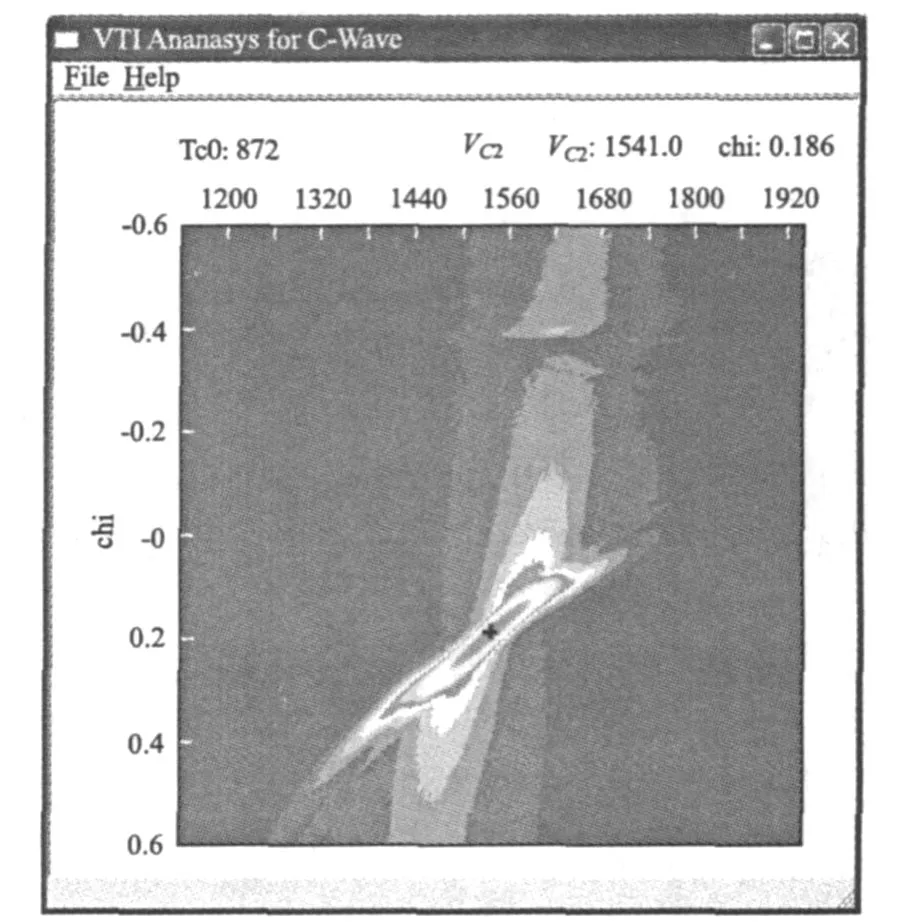
图3 VC2,χeff双参数扫描Fig.3 Double-scanning forVC2,χeff

表1 三层VTI介质模型Tab.1 Three-layer model of VTI media

由以上分析可知,双参数扫描γ0和γeff时,分辨率和精度差,而扫描VC2和χeff时分辨率高。作者认为,之所以有这样的差别,是因为VC2控制着近炮检距部份,而χeff控制着远炮检距部份,所以双参数扫描VC2、χeff时能够获得较高的分辨率和精度。而由于γ0和γeff对时距曲线的作用基本相同,且均控制着中炮检距部份,这就是γ0、γeff双参数扫描分辨率不高的原因。由此可知,欲采用双参数扫描法获得较高的分辨率和精度,所满足的必要条件是:这二个参数作用差别较大,或者分别控制着不同炮检距部份的时距曲线。

从以上分析可知,从C波资料中求得γ0和γeff比较困难,有很多学者都建议通过纵、横波剖面对比来确定γ0,然后作进一步的处理。但是纵、横波剖面对比并不是一项简单的工作,所以C波参数估计问题仍比较复杂。

1.2 VTI介质简化的C波旅行时公式

考虑γ0和γeff的作用基本相同,所以XY-Li在2003年又同时推导出简化的方程[4],将γ0和γeff综合考虑成γiso,如式(4):

式中

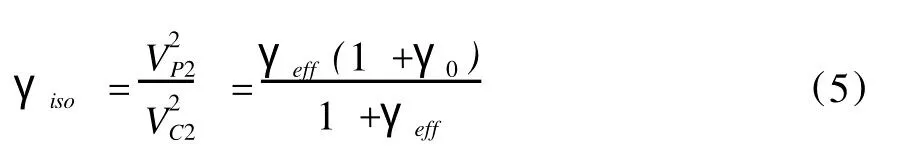
当γiso=1时,方程(4)退化成双曲线,由此可知时距曲线对γiso的变化较为敏感,所以可以通过扫描法来确定γiso。当tC0固定并已知χeff时,在x/z<2.0范围内双参数扫描VC2、γiso,可获得较高的分辨率和精度。采用表1的模型参数,双参数扫描VC2、γiso,图4～图6(见下页)分别为1层-3层的扫描结果,可见VC2的误差小于1%。

于是利用式(4)可以直接处理C波资料,而不需依赖于P波。在求得VC2及γiso的基础上,可以用单参数扫描法求取χeff。用此法求取的各参数对道集做动校正,如下页图7所示,可见同相轴已经被校平。

但是,以上所述的双参数扫描,是在固定的层位进行的(即已知tC0)。可见建立合适的层位模型,是求取有效速度比γiso和各向异性系数χeff的关键问题之一。为了建立合适的层位模型,可以用非双曲方程对C波进行各向同性分析。此法不仅可以建立合理的层位模型,还可以求取比较精确的C波动校速度VC2。

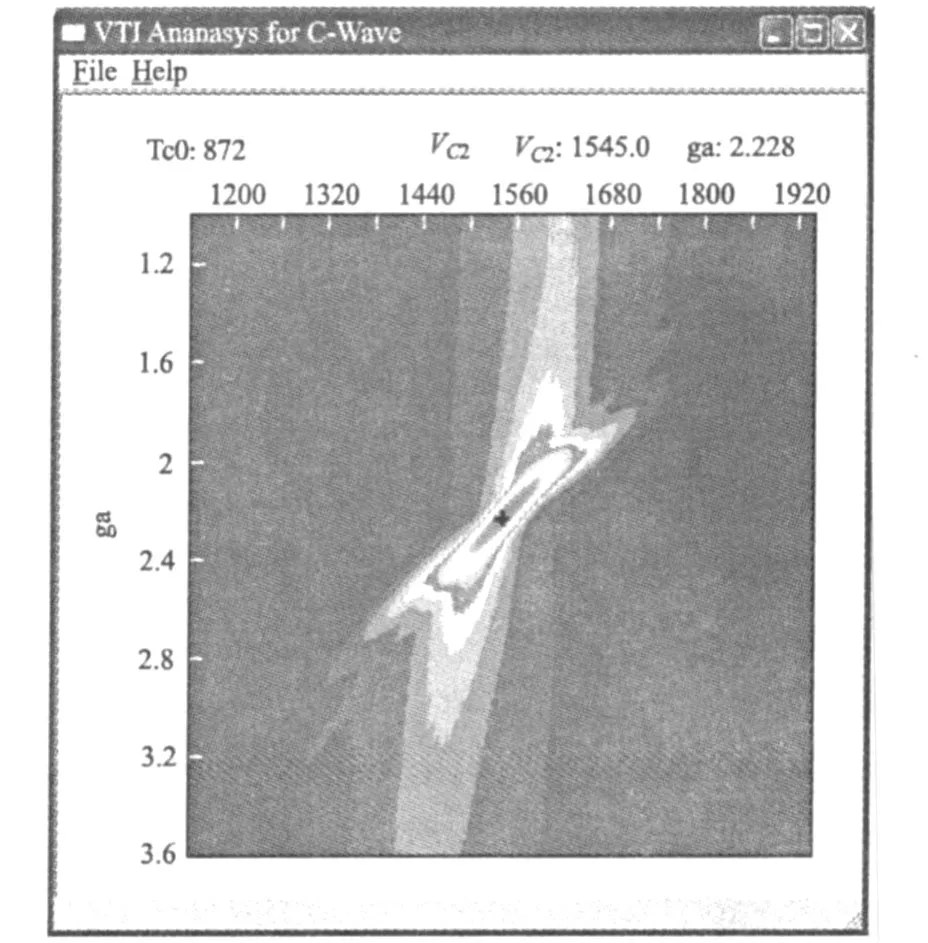
图4 第1层VC2、γiso双参数扫描Fig.4 Double-scanning for VC2,γisoat reflector 1

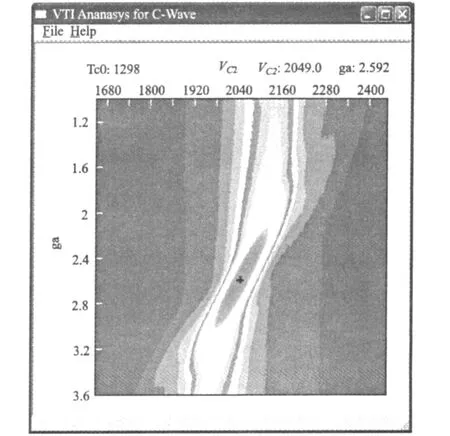
图5 第2层VC2、γiso双参数扫描Fig.5 Double-scanning for VC2,γisoat reflector 2

1.3 C波各向同性分析

在四参数方程中,若令χeff=0,γ0=γeff=γ时,则可证明方程退化为

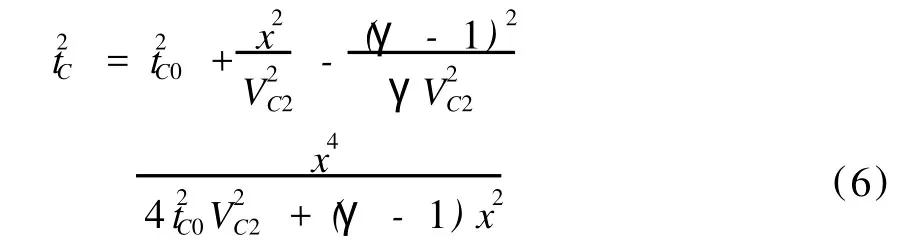
这就是各向同性单层情况下的时距曲线。即使存在各向异性情况下,该方程在x/z<1.5范围内都是精确的[4]。

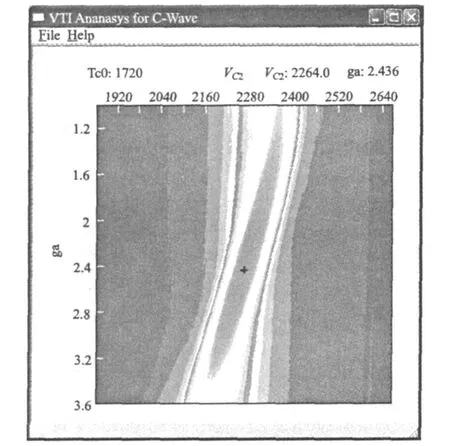
图6 第3层VC2、γiso双参数扫描Fig.6 Double-scanning forVC2,γisoat reflector 3

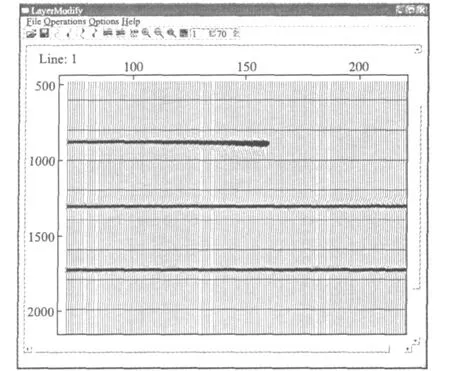
图7 动校正道集Fig.7 NMO gather

为了检验该方程的精度和γ的敏感性,我们取各向同性单层模型

(1)模型一:tC0=1.5,VP=1800,VS=500,VC2=948.68,γ=3.6。我们分别取γ=3.6、γ=4.0和γ=3.2,如图8所示。在图8中,横坐标为x/z,纵坐标为用该方程计算的tC与真实值之差。从图8中可以看出,当γ=3.6时,x/z<1.5以内有较好的精度;当γ=4.0时,在x/z<1.3以内有较好的精度;当γ=3.2时,x/z<2.5以内时距曲线从整体上有较好的精度。

(2)模型二:取tC0=1.5,VP=1 800,VS=1 000,VC2=1 341.64,γ=1.8。我们分别取γ=1.8、γ=2.0和γ=1.6,如图9所示。从图9中可以看出,当γ=1.8时,在x/z<2.5以内有较好的精度;当γ=2.0时,x/z<1.5以内有较好的精度;当γ=1.6时,x/z<1.5以内有较好的精度。

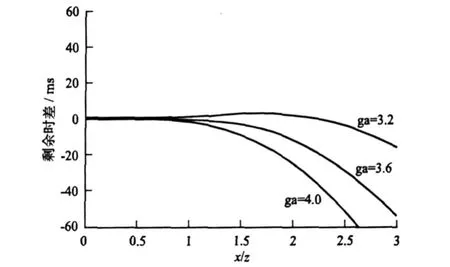
图8 模型一中方程(6)的精度分析Fig.8 Precision analysis of Eq.(6)formodel 1

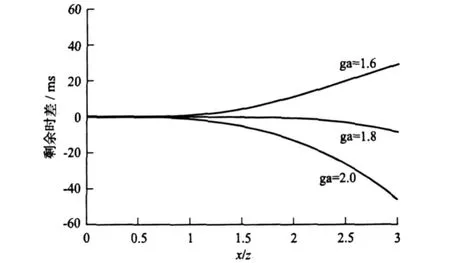
图9 模型二中方程(6)的精度分析Fig.9 Precision analysis of Eq.(6)formodel 2

从图8、图9中可以得出三点结论:

(1)该方程的效果大大好于双曲近似,能够在x/z<1.5甚至更大的范围内适用。

(2)γ具有10%～15%的扰动,在x/z<1.0以内对时距曲线基本没有影响,在x/z<1.5以内影响也不大,γ适当偏小甚至能在更大范围内逼近真实曲线。

(3)VP/VS越趋近于1,该方程越具有更强的拟合能力,能在更大范围内与真实曲线重合。不难理解,γ趋近于1时,与P波时距曲线方程相同,为严格的双曲线。正是因为如此,当纵、横波速度比越小时,该方程越准确,对于同样的深度可以拟合的炮检距越大。

考虑到该方程的特点,所以有可能估计一个γ来对转换波进行处理,求得较为精确的VC2并建立合理的层位模型以便于随后的各向异性分析。用此方程在x/z<1.5范围内求出的VC2的误差小于1%[3]。值得注意的是,由于在深层即tC0较大时,非双曲线效应的参数变化,对时距曲线的影响减弱了,所以可将γ取得贴近浅层情况。

我们取表1中的三层VTI介质模型,取γ=2.2,用方程(6)做速度分析,求取速度谱,并用交互的方法拾取速度,再动校正,处理结果如图10所示。可见,效果大大好于双曲近似,双曲近似如图11所示。

图10 用方程(6)做动校正Fig.10 Nmo gather using Eq.(6)

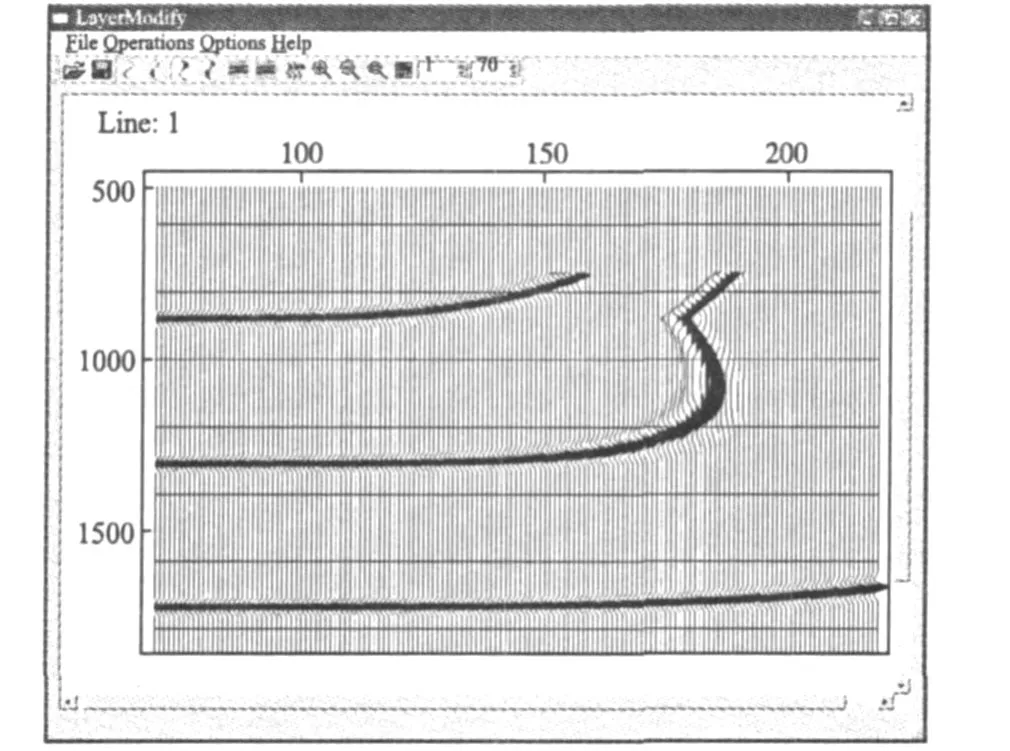
图11 双曲线近似动校正Fig.11 Nmo gather using hyperbolic equation

2 C波速度分析步骤及应用实例

综合上述分析,我们提出建立C波叠加速度模型的步骤。

(1)估算一个γ,并将x/z限制在1.5范围内,采用方程(6)做各向同性分析,建立初始的速度模型和较为准确的层位模型。

(2)在已知VC2和层位模型的基础上,将x/z限制在2.5范围内,用方程(6)双参数扫描VC2和γ(此γ相当于方程(4)中χeff=0时的γiso),并将扫描结果作为各向异性分析的输入。

(3)用方程(4)做各向异性速度分析,将x/z限制在3.0范围内,在VC2和γiso确定的情况下,单参数扫描χeff,求得各向异性系数。

(4)采用批处理和交互的方法来保证处理精度。如有必要,可迭代处理,以交互软件求得的参数再进行速度分析,求得最终的C波叠加速度模型。

该步骤使得C波速度分析完全独立于纵波数据,避免了采用方程(1)做速度分析时,用纵、横波剖面对比来确定γ0,直接从转换波中求取各参数,从而进一步简化了处理流程,而且也可以取得较好的处理效果。

用该方法和开发的软件对某地区转换波资料进行处理,求取速度谱,并用交互软件进行分析,如图12所示。图12中从图12(a)～图12(c)分别为速度谱、CDP道集和动校正道集。

图12 交互速度分析图Fig.12 Interactive velocity analysis

在tC0=3 260 ms处,双参数扫描VC2、γiso,如图13(见下页)所示。在图13中,VC2、γiso的分辨率较模型数据差,其原因在于当tC0较大时,非双曲线效应的参数变化对时距曲线的影响减弱了。若远端同相轴还未校平,则调整χeff使远端同相轴校平。

我们分别采用常规方法和该新方法对实际资料进行处理,得出的叠加剖面分别如下页图14和图15所示,可见,新方法处理的转换波资料同相轴更加清晰、连续,效果更好。

图13 VC2、γiso双参数扫描Fig.13 Double-scanning forVC2andγiso

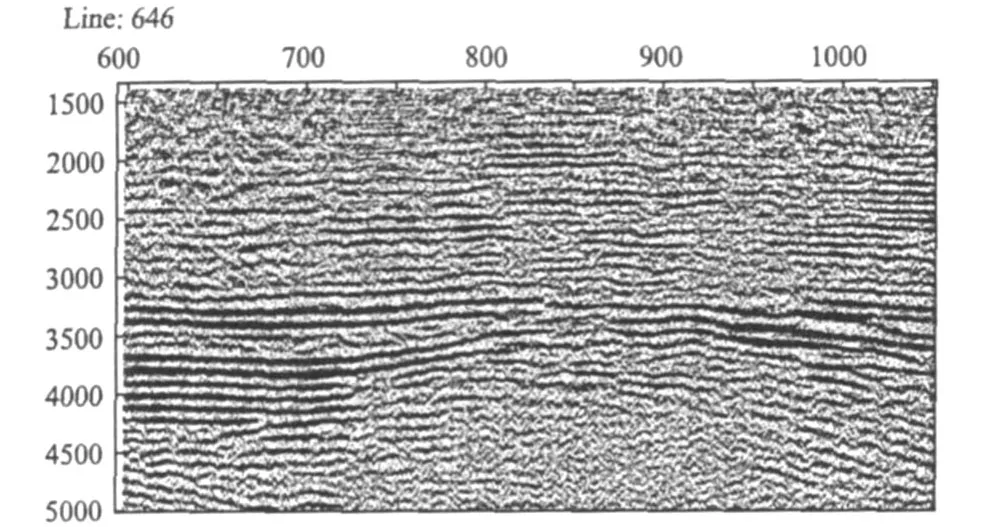
图14 常规方法处理的叠加剖面Fig.14 Stack profile using conventional method

图15 新方法处理的叠加剖面Fig.15 Stack profile using new method

3 结论

作者在本文中对XY-Li方程及其简化方程分析的基础上,形成了一套从各向同性分析到各向异性分析的C波速度分析和动校正方法,该方法不依赖于纵波数据,大大提高了转换波处理的效率,而且可以取得较高的精度。该方法可以同时求取C波动校速度、纵横波速度比和各向异性系数。如有必要还可以结合纵波数据求取更多的参数,从而为偏移和岩性预测等进一步的处理打下基础。

[1] TSVANKIN I,THOMSEN L.Nonhyperbolic reflection moveout in anisotropic media[J].Geophysics,1994,59:1290.

[2] THOMSEN,L.Converted-wave reflection seis mology over inhomogeneous,anisotropic media[J].Geophysics,1999,64:678.

[3] LIX Y,YUAN J.Converted-wave moveout and conversion-point equations in layered VTI media:theory and application[J].Journal of Applied Geophysics,2003,54:297.

[4] LIX Y,YUAN J.Converted-wave moveout analysis revisited:the search for a standard approach.73th Annual Internat[M].Mtg:SEG,Expanded Abstracts,2003.

[5] LIX Y,YUAN J.Converted-wave seismology in anisotropic media revisited:Application to parameter estimation[J].Applied Geophysics,2005,2(3):153.

[6] 李录明,罗省贤.多波多分量地震勘探原理及数据处理方法[M].成都:成都科技大学出版社,1997.

[7] 李录明,罗省贤.P-SV转换波速度分析方法及解释方法[J].石油地球物理勘探,1995,30(1):66.

[8] 罗省贤,李录明,陈春继.VTI介质多波速度与各向异性系数求取及应用[J].物探化探计算技术,2005,27(3):214.

[9] L IX Y,YUAN J.Converted-wave seismology in anisotropic media revisited:Basic Theory[J].Applied Geophysics,2005,2(1),26.