一类延时积分方程的外推算法

肖继红,王李会,吕 涛

(1.四川大学锦江学院,四川彭山 620860;2.四川泸县第六中学,四川泸州 646107; 3.四川大学数学学院,四川成都 610064)

0 引 言

对积分方程的处理中,有很大一部分是积分限带有延迟项的延时积分方程.本文研究了下述的延时积分方程,

对于延时积分方程(1),其既不同于Fredholm方程,也不同于Volterra积分方程.目前,延时方程在随机过程、生态学、生物数学等方面有重要的应用, Brunner[1,12,14]对此有详细的阐述.Andreoli[2]通过Picard迭代核的方法揭示了方程(1)的解非常复杂. Chambers[3]对方程(1)的解采用级数解,且只是理论上的一个解.目前,学者在延时积分方程的算法的研究中,取得了大量的研究成果,如从稳定性方面考虑可参阅徐道义[11]、匡蛟勋[5,15]的相关研究.

本文用数值方法分析方程(1)的算法,通过对该方程的算法分析并与文献[10]进行对比,文献[10]中收敛阶只达到 O(h),本文收敛阶能达到O(h2),同时,通过外推技术,可使收敛的误差达到更高的精度.理论和算例表明,外推技术具有节约存储量、减少计算量、降低计算复杂度等优点.

1 方程的离散算法

利用Banach不动点原理证明延时积分方程(1)的存在性和唯一性.首先引入Lipschitz条件:假设核K(t,s′,·)连续,且对固定的s,t,存在0＜L＜1满足Lipschitz条件,

定理1 设 u∈C3[0,T],核 K(t,s′,u)关于变量t,s连续,且对u满足Lipschitz条件,则方程(1)存在唯一解.

证 令,

则有,

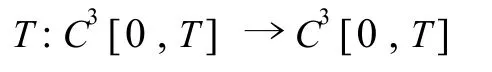
取ρ(u,v)表示距离,则有,

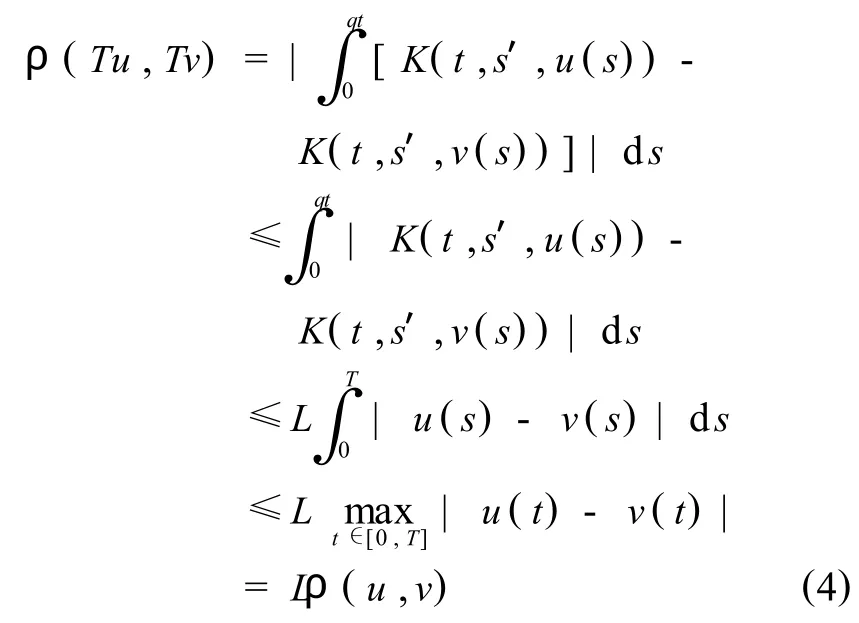
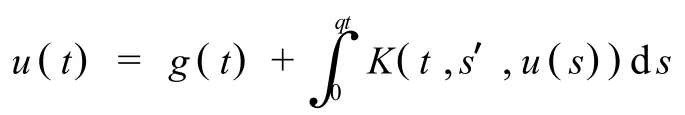
存在唯一解.

下面对方程(1)采用中矩形公式[4]离散.

式中,[qi]表示不超过 qi的最大整数.

然后,对积分 I1、I2进行离散化.在[0,t[qi]], [t[qi],qti]上均采用中矩形公式,可得到,

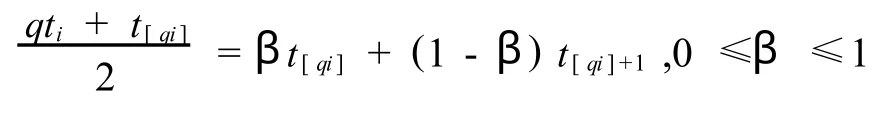
定理2 设 u∈C3[0,T],β∈[0,1],x,y∈[0,T],且有 z=βx+(1-β)y.则成立,

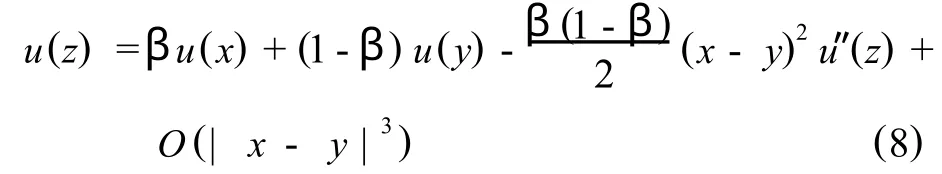
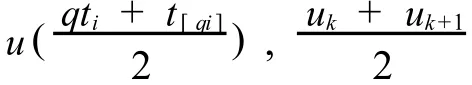
方程(9)是一个非线性方程,uj,j=0,1,…,N,可通过下面的迭代算法计算,其计算步骤为:

步骤1 置充分小的ε＞0,u0=g(t0),i:=1.

步骤2 置u0i= ui-1,m:=0,um+1i(i≤N)通过下面的简单迭代计算,

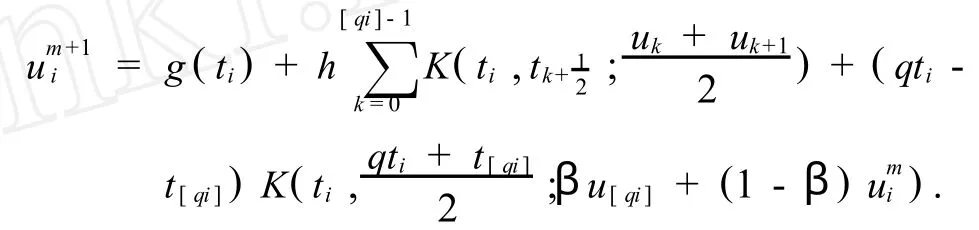
步骤3 假设有|umi+1-umi|≤ε,置 ui:= umi+1,且i:=i+1,继续步骤2;否则,置m:=m+ 1,进行步骤2.

2 收敛性分析,渐进展开式和外推技术

先给出Euler-Maclaurin求和展开式[6,7],其也是外推和后验误差估计的基础.

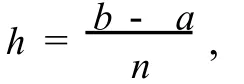
定理4 设核 K(t,s′,·)∈C3[0,T]×[0,T],且满足Lipschitz条件(2).记ei=u(ti)-ui为算法的误差,则存在不依赖于 h的常数CM＞0,使得,

证 分别对 I1、I2用中矩形公式渐进展开,I1, I2分别有渐进误差 EI1、EI2,由引理3,可知,

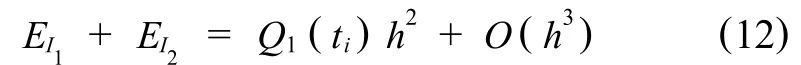
式中

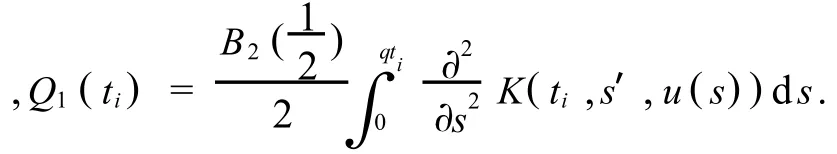
由定理2可知,

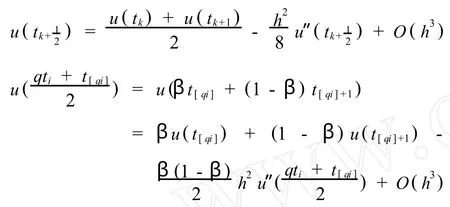
由Taylor展开式可以得到下面的式子,

式中:

用(13)式减去(9)式,可以得到误差{ei}满足的方程组:

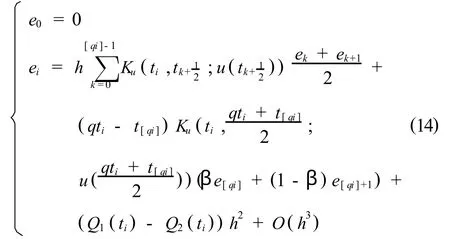
两边取绝对值,由Lipschitz条件,可以得到{ei}所满足的不等式组:

取,

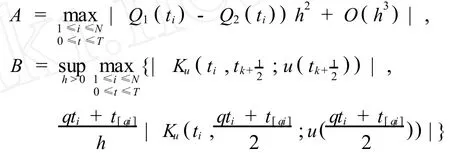
则有,

由离散Gronwall不等式[8,9]可得,

对于某个不依赖于 h的常数CM＞0,得到,

即得到定理的证明.

下面进一步考虑外推和后验误差估计.

对已知的 u(t),首先考虑下面的辅助问题,设Q∧k(t),k=1,2,满足下述的延时积分方程,

并且Q∧k(ti)满足它的近似方程,

用与定理4相类似的方法,可得到,

把式(20)代入式(14)中,可以得到,

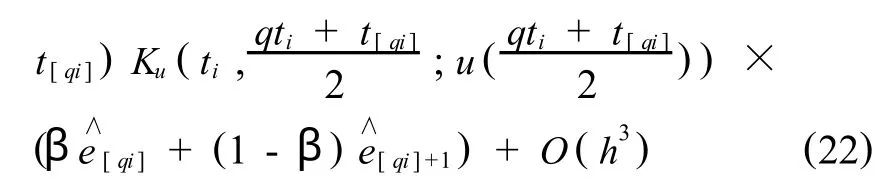
由离散Gronwall不等式,存在常数 C满足,

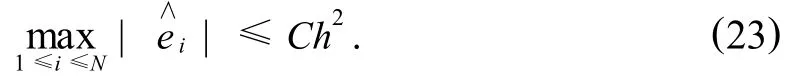
由此可以得到,

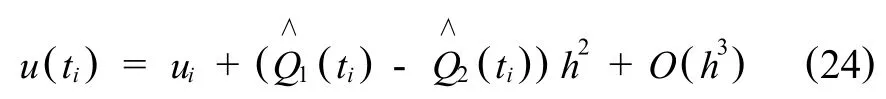
由上面的讨论,我们可以得到下面的定理.

定理5 设方程(1)的解u=C3[0,T],且 K,g∈C3[0,T],K(t,s′,u(s))对 u满足Lipschitz条件,则存在不依赖于步长 h的函数满足渐进展开式Q∧(t)满足式(24).

式(24)意味着对于算法可以采用Richardson-h2外推技术,并可得到更高的精度,有,

式中,uhi/2与uih是在式(13)中分别用h/2与h算出来的.由式(25),uei-u(ti)有精度 O(h3).因此,可以得到后验误差估计,

3 数值算例

为了说明本算法的有效性,考虑下面的延时积分方程

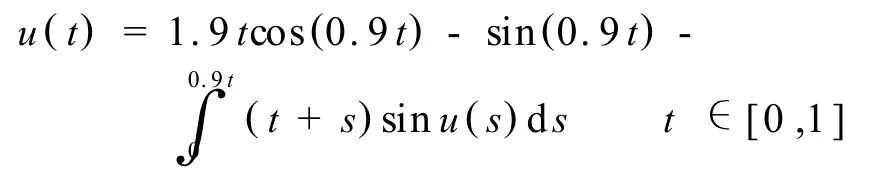
该方程有精确解 u(t)=t.采用数值算法算出h=0.05和 h=0.025时的数值结果与误差如表1所示.

从表1看出,最小误差比为3.67,与理论值4= 22接近,这说明算法的代数精度是2,与定理2吻合.同时,通过外推,精度能得到大大的提升,这充分说明外推在提高精度方面是非常有效的.

表1 方程数值解的结果与误差

[1]Brunner H.Collocation Methods forVolterra Integral and Related Functional Differential Equations[M].London:Cambridge University Press,2004.

[2]Andreoli G.Sulle Equazioni Integrali[J].Rend Cire Mat Palermo,1914,37(1):76-112.

[3]Chambers L G.Some Properties of the Functional EquationØ (x)=f(x)+∫λx0g(x,y,Ø(y))dy[J].Internat J Math Math Sci,1990,14(1):27-44.

[4]Kress R.Linear Integral Equations[M].Berlin:Springer-Verlag Press,1989.

[5]KuangJ X,Cong Y H.Stability of Numerical Methods for Delay Differenial Equations[M].Beijing:Science Press,2005.

[6]吕 涛,石济民,林政宝.分裂外推与组合技巧[M].北京:科学出版社,1998.

[7]Liem C B,LüT,Shih T M.The Splitting Extrapolation Method [M].Singapore:World Scientific Publishing,1995.

[8]LüT,Huang Y.A Generalization of Discrete Grownwall Inequality and Its Application to Weakly Singular Volterra Inregral Equation of the Second kind[J].J Math Anal Appl,2003,282(1):56-62.

[9]LüT,Huang Y.Extrapolation Method for Solving Weakly Singular NonlinearVolterra Integral Equations of the Second kind[J].J Math Anal Appl,2006,324(1):225-237.

[10]刘亚平.第一类弱奇异Volterra积分方程的超收敛技术[D].成都:四川大学,2006.

[11]Xu Daoyi.Integro-differential Equations and Delay Integral Inequalities[J].Iǒhuku Math J,1992,44(3):365-378.

[12]马知恩.种群生态学的数学建模与研究[M].合肥:安徽教育出版社,1996.

[13]Brunner H,Hu Qiya,Lin Qun.Geometric Meshes in Collocation Methods for Volterra Integral Equations with Proportional Delays [J].IMA J Numer Anal,2001,21(4):783-798.

[14]范振成.随即延迟微分方程的全隐式 Euler方法[J].计算数学,2009,31(3):287-298.

[15]田红炯,匡蛟勋.滞时Volterra积分方程数值方法的数值稳定性分析[J].应用数学与力学,1995,16(5):451-457.